Schetsen van "tuych‑werckelycke" kegelsneden

Henk Hietbrink, Sep 18, 2025

Frans van Schooten Junior heeft zijn boek [i]Mathematische Oeffeningen[/i] rijk geïllustreerd met veel schetsen. In het vierde boek presenteerde hij zijn "tuych‑werckelycke" beschrijving van de kegelsneden. Dat waren kegelsneden die met een werktuig gemaakt konden worden. Hij schetste constructies van stangen en latten en touwen die met pinnen op het tekenpapier werden vastgezet. Een overzicht van alle constructies staat op [url]https://www.fransvanschooten.nl/fvs_tekeningen4.htm[/url]

Table of Contents

  1. Rechte Lijnen
    1. fvs_283: Van rechte linien
  2. Ellipsen
    1. fvs_299 Ellipsograaf van Frans van Schooten
    2. fvs_300 Ellipsograaf van Frans van Schooten
    3. fvs_301 Ellipsograaf van Frans van Schooten
    4. fvs_302: Tuinman's Ellips van Frans van Schooten
    5. fvs_315 Ellipsograaf van Frans van Schooten
    6. fvs_318: Ellipsograaf van Frans van Schooten
    7. fvs_300: Ellipsograaf van Simon Stevin
    8. Ellipsograaf van Viktor Blåsjö
  3. Parabolen
    1. fvs_331: Parabolograaf Frans van Schooten
    2. fvs_334 Parabolograaf Frans van Schooten
  4. Hyperbolen
    1. fvs_311 Hyperbolograaf van Frans van Schooten
    2. fvs_314 Hyperbolograaf van Frans van Schooten
    3. fvs_320 Hyperbolograaf van Frans van Schooten
    4. fvs_324: Hyperbolograaf Frans van Schooten
    5. Hyperbolograaf van Viktor Blåsjö
    6. fvs_307_descartes
  5. Begrippen
    1. fvs_288_ellips: uitleg begrippen ellips

1.

Rechte Lijnen

Frans van Schooten (1615-1660) laat zien dat je met een constructie van bewegende stokken een rechte lijn kan tekenen. [url]https://www.fransvanschooten.nl/fvs_tekeningen4.htm[/url]

  • 1. fvs_283: Van rechte linien

1.1.

fvs_283: Van rechte linien

Frans van Schooten beschreef hoe je met eenvoudige instrumenten ellipsen, parabolen en hyperbolen kon tekenen en benutte alle eigenschappen van kegelsnedes. Beschrijving, toelichting en bewijs staan op [url=http://www.fransvanschooten.nl/fvs_283.htm]http://www.fransvanschooten.nl/fvs_283.htm[br][br][/url]Gebruik het handje bij het rode punt om de constructie in beweging te brengen. Je kunt de groene punten gebruiken om de constructie te verplaatsen.
Getoond wordt hoe een bewegende stok een rechte lijn kan produceren.[br]Essentieel is dat punt B op een cirkel ligt en dat er sprake is van twee complementaire gelijkbenige driehoeken.[br][br]Een overzicht van alle constructies staat op de webpagina [url=https://www.fransvanschooten.nl/fvs_tekeningen4.htm ]fvs_tekeningen4.htm[/url]
– Henk Hietbrink

2.

Ellipsen

Frans van Schooten (1615-1660) laat zien dat je op verschillende manieren met een constructie van bewegende stokken een ellips kan tekenen. [url]https://www.fransvanschooten.nl/fvs_tekeningen4.htm[/url]

  • 1. fvs_299 Ellipsograaf van Frans van Schooten
  • 2. fvs_300 Ellipsograaf van Frans van Schooten
  • 3. fvs_301 Ellipsograaf van Frans van Schooten
  • 4. fvs_302: Tuinman's Ellips van Frans van Schooten
  • 5. fvs_315 Ellipsograaf van Frans van Schooten
  • 6. fvs_318: Ellipsograaf van Frans van Schooten
  • 7. fvs_300: Ellipsograaf van Simon Stevin
  • 8. Ellipsograaf van Viktor Blåsjö

2.1.

fvs_299 Ellipsograaf van Frans van Schooten

Frans van Schooten beschreef hoe je met eenvoudige instrumenten ellipsen, parabolen en hyperbolen kon tekenen en benutte alle eigenschappen van kegelsnedes. Beschrijving, toelichting en bewijs staan op [url=http://www.fransvanschooten.nl/fvs_299.htm]http://www.fransvanschooten.nl/fvs_299.htm[br][/url][br]Gebruik het handje bij het rode punt om de constructie in beweging te brengen. Je kunt de groene punten gebruiken om de constructie te verplaatsen.
Getoond wordt hoe je met een potloodje en een bewegende stok een ellips kan produceren.[br]Achterliggend idee is dat de vorm van de ellips ligt vast als de lange en korte diameter gegeven zijn.[br]Essentieel in deze constructie is dat de twee stokken even lang zijn en dat het gaatje voor het potlood in verticale stand op de plek van de korte as ligt en in horizontale stand op de plek van de lange as.[br][br]Een overzicht van alle constructies staat op de webpagina [url=https://www.fransvanschooten.nl/fvs_tekeningen4.htm]fvs_tekeningen4.htm[/url]
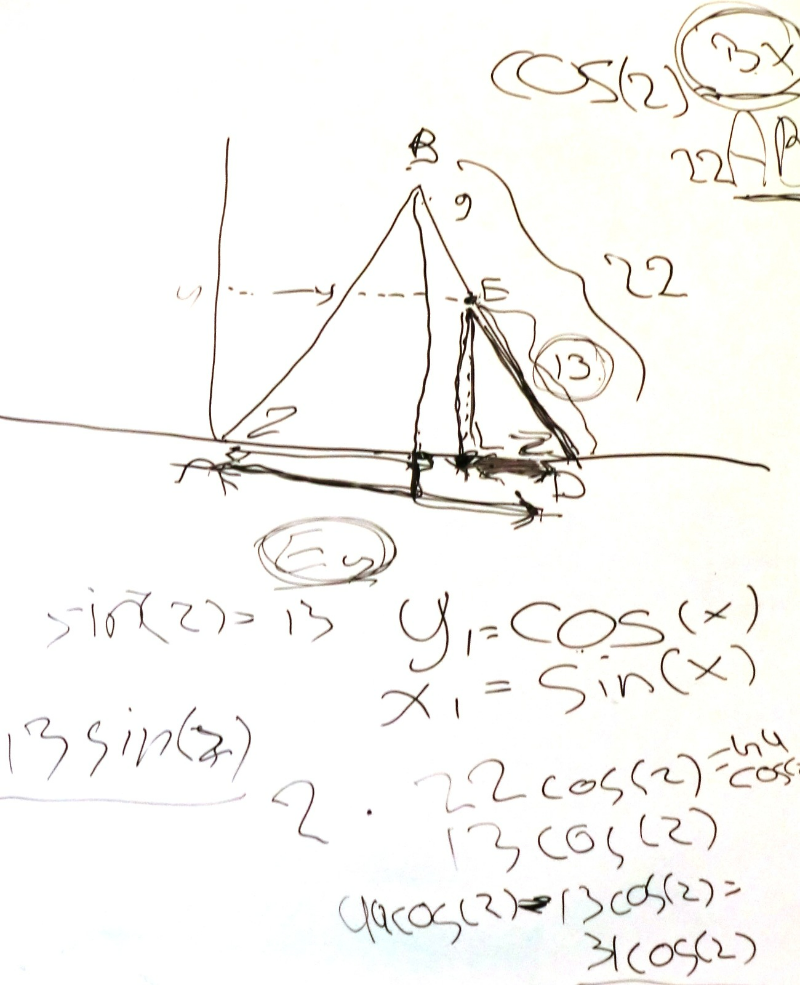
Leerlingen zijn op zoek naar het verband tussen de meetkundige eigenschappen van een ellips en de algebraïsche.
– Henk Hietbrink

2.2.

–

2.3.

–

2.4.

–

2.5.

–

2.6.

–

2.7.

–

2.8.

–

3.

Parabolen

Frans van Schooten (1615-1660) laat zien dat je op verschillende manieren met een constructie van bewegende stokken een parabool kan tekenen. [url]https://www.fransvanschooten.nl/fvs_tekeningen4.htm[/url]

  • 1. fvs_331: Parabolograaf Frans van Schooten
  • 2. fvs_334 Parabolograaf Frans van Schooten

3.1.

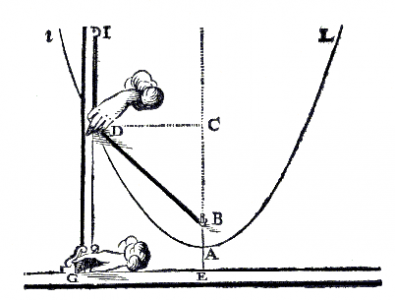
fvs_331: Parabolograaf Frans van Schooten

Frans van Schooten beschreef hoe je met eenvoudige instrumenten ellipsen, parabolen en hyperbolen kon tekenen en benutte alle eigenschappen van kegelsnedes. Beschrijving, toelichting en bewijs staan op [url=http://www.fransvanschooten.nl/fvs_331.htm]http://www.fransvanschooten.nl/fvs_331.htm[/url][br][br]Gebruik het handje bij het rode punt om de constructie in beweging te brengen. Je kunt de groene punten gebruiken om de constructie te verplaatsen.[br]
Getoond wordt hoe een constructie van bewegende stokken een parabool kan produceren.[br][br]Een overzicht van alle constructies staat op de webpagina [url=https://www.fransvanschooten.nl/fvs_tekeningen4.htm]fvs_tekeningen4.htm[/url][br]
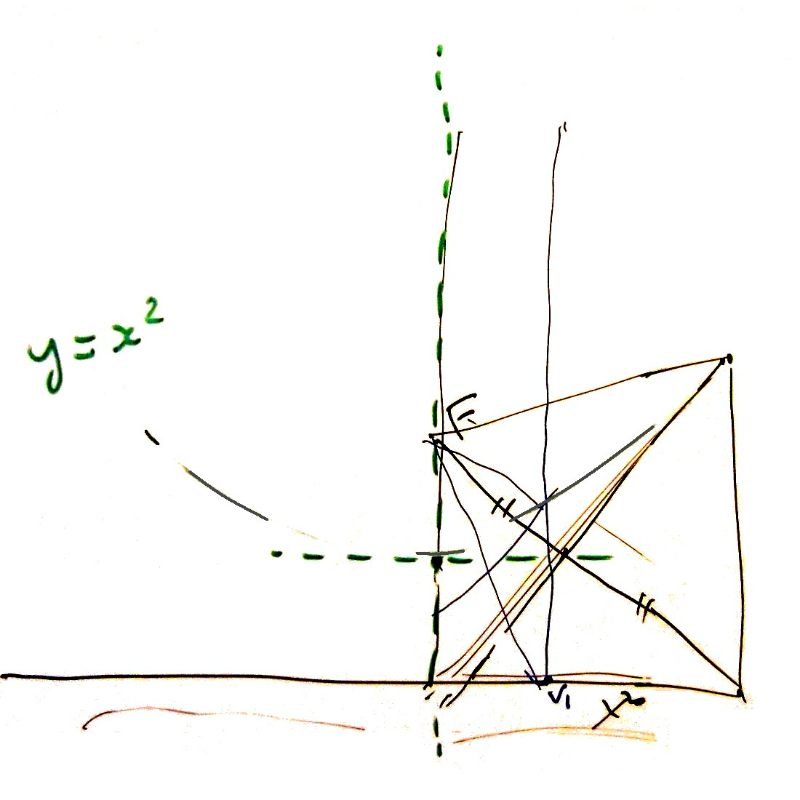
Leerlingen zoeken naar het verband tussen de meetkundige eigenschappen van de parabool en de algebraïsche.
– Henk Hietbrink

3.2.

–

4.

Hyperbolen

Frans van Schooten (1615-1660) laat zien dat je op verschillende manieren met een constructie van bewegende stokken een hyperbool kan tekenen. [url]https://www.fransvanschooten.nl/fvs_tekeningen4.htm[/url]

  • 1. fvs_311 Hyperbolograaf van Frans van Schooten
  • 2. fvs_314 Hyperbolograaf van Frans van Schooten
  • 3. fvs_320 Hyperbolograaf van Frans van Schooten
  • 4. fvs_324: Hyperbolograaf Frans van Schooten
  • 5. Hyperbolograaf van Viktor Blåsjö
  • 6. fvs_307_descartes

4.1.

fvs_311 Hyperbolograaf van Frans van Schooten

Frans van Schooten beschreef hoe je met eenvoudige instrumenten ellipsen, parabolen en hyperbolen kon tekenen en benutte alle eigenschappen van kegelsnedes. Beschrijving, toelichting en bewijs staan op [url=http://www.fransvanschooten.nl/fvs_311.htm]http://www.fransvanschooten.nl/fvs_311.htm[/url] [br][br]Gebruik het handje bij het rode punt om de constructie in beweging te brengen. Je kunt de groene punten gebruiken om de constructie te verplaatsen.
Getoond wordt hoe je met een potloodje en een constructie van bewegende stokken een hyperbool kan produceren.[br][br][br]Een overzicht van alle constructies staat op de webpagina [url=https://www.fransvanschooten.nl/fvs_tekeningen4.htm]fvs_tekeningen4.htm[/url][br]
– Henk Hietbrink

4.2.

–

4.3.

–

4.4.

–

4.5.

–

4.6.

–

5.

Begrippen

  • 1. fvs_288_ellips: uitleg begrippen ellips

5.1.

fvs_288_ellips: uitleg begrippen ellips

fvs_288_ellips: uitleg begrippen ellips[br][url=http://www.fransvanschooten.nl/fvs_288.htm]http://www.fransvanschooten.nl/fvs_288.htm[/url]
– Henk Hietbrink

Information