Anche lo spazio , analogamente al piano, può essere rappresentato con un tipo di riferimento cartesiano utilizzando tre rette orientate, a due a due perpendicolari tra loro che, per convenzione, chiamiamo x, y e z. Il punto in cui si intersecano le tre rette, prende il nome di[b] origine.[/b][br]

Per individuare un punto P nello spazio, abbiamo bisogno di tre coordinate: P(x[sub]p[/sub], y[sub]p[/sub], z[sub]p[/sub])[br]-x[sub]p[/sub] è detta ascissa;[br]-y[sub]p è detta ordinata;[br][/sub]-z[sub]p è detta quota.[/sub]

Pertanto, la distanza tra due punti A(x[sub]A[/sub], y[sub]A[/sub], z[sub]A[/sub]) e B(x[sub]B[/sub], y[sub]B[/sub], z[sub]B[/sub]), si calcola come:[br][math]AB=\sqrt{\left(xa-xb\right)^2+\left(ya-yb\right)^2+\left(za-zb\right)^2}[/math][br][br][br][br]

A ogni punto nello spazio è possibile associare un vettore che abbia come primo estremo l'origine O degli assi cartesiani.[br]I versori, per ogni asse, assumono un nome diverso:[br]- i -> asse x;[br]- j -> asse y;[br]-k -> asse z.[br]Un vettore è espresso come:[br][math]v^{\rightarrow}=v_xi^{\rightarrow}+v_yj^{\rightarrow}+v_zk^{\rightarrow}[/math]

Tra due o più vettori si possono fare anche le varie operazioni:[br][b]-SOMMA: [math]a^{\rightarrow}+b^{\rightarrow}=\left(ax+bx;ay+by;az+bz\right)[/math][br]-DIFFERENZA: [math]a^{\rightarrow}-b^{\rightarrow}=\left(ax-bx;ay-by;az-bz\right)[/math][br]-PRODOTTO PER UNO SCALARE: [math]ka^{\rightarrow}=\left(kax;kay;kaz\right)[/math][br][/b][b]-PRODOTTO SCALARE: [math]a^{\rightarrow}\cdot b^{\rightarrow}=axbx+ayby+azbz[/math][br]-PRODOTTO VETTORIALE:[math]a^{\rightarrow}\times b^{\rightarrow}=\left(aybz-azby\right)i^{\rightarrow}-\left(axbz-azbx\right)j^{\rightarrow}+\left(axby-aybx\right)k^{\rightarrow}[/math][br][/b]

[br][br][br][b]VETTORI PARALLELI[br][math]a^{\rightarrow}\slash\slash b^{\rightarrow}\Leftrightarrow\frac{ax}{bx}=\frac{ay}{by}=\frac{az}{bz}[/math][/b][br][br][b]VETTORI PERPENDICOLARI[br][math]a^{\rightarrow}\bot b^{\rightarrow}\Leftrightarrow axbx+ayby+azbz=0[/math][br][/b]

L'equazione generale di un piano passante per un punto P(x[sub]0[/sub];y[sub]0[/sub];z[sub]0[/sub]) e avente vettore normale [size=85]n[/size][math]^{\rightarrow}[/math](a;b;c) non nullo è:[br][math]a\left(x-x_0\right)+b\left(y-y_0\right)+c\left(z-z_0\right)=0[/math] con a, b e c numeri reali non tutti nulli.[br][br]Svolgendo i calcoli otteniamo:[br][math]ax+by+cz-ax_0-by_0-cz_0=0[/math]  poniamo [math]d=-ax_0-by_0-cz_0[/math] e otteniamo:[br][br][math]ax+by+cz+d=0[/math]

[br]I piani possono essere:[br][b]-PARALLELI:[br][math]\frac{a}{a^'}=\frac{b}{b^'}=\frac{c}{c^'}[/math][br]-PERPENDICOLARI:[br] [math]aa^'+bb^'+cc^'=0[/math][/b]

Dato un piano [math]\alpha[/math] di equazione ax+by+cz+d=0 e il punto A(x[sub]a[/sub];y[sub]a[/sub];z[sub]a[/sub]), la loro distanza è calcolabile come:[br][math]d\left(A,\alpha\right)=\frac{\left|ax_a+by_a+cz_a+d\right|}{\sqrt{a^2+b^2+c^2}}[/math]

Una retta passante per un punto P(x[sub]0[/sub];y[sub]0[/sub];z[sub]0[/sub]) e un vettore [math]v^{\rightarrow}[/math](l;m;n) non nullo, ha equazioni parametriche:[br]

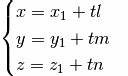
ed equazioni cartesiane, valide se l, m, n[math]\ne[/math]0:[br][math]\frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}[/math]

Considerando due punti A(x[sub]a[/sub];y[sub]a[/sub];z[sub]a[/sub]) e B(x[sub]b[/sub];y[sub]b[/sub];z[sub]b[/sub]), la retta passante per questi due punti ha equazione:[br][math]\frac{x-x_A}{x_B-x_A}=\frac{y-y_A}{y_B-y_A}=\frac{z-z_A}{z_B-z_A}[/math][br]che sono le [b]condizioni di allineamento[/b] di tre punti A, B, P(x; y; z).

Una retta può anche essere individuata come intersezione di due piani non paralleli:[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJ4AAAAlCAYAAACziFDNAAAFeElEQVR4Ae2a3VEcMRCECcMEYkKw300gJggeCYREiIAMiIFX6lwfVe2bmhv9nFbSrrFUtV6tNNMz09Org8M3pzUWAzswcLNDzBVyMXBawlsi2IWBIcJ7e3s7PT09nV5eXqYWRbyHh99TY44K9vz8/GVqiTgaIjxEB3GzB8K7u/veHJYXZtS4FntrLaqDuLyM9OPaHIQx4j5EeDS/d5E0oiRm9hF968C3d97KhdyooXZg2+P0vr//9RlSAqyNP9puqvAo3guINTXbzn3h3s/v84xwJDzsI1ytpfxz+/LBxr4EEhXrxI2GbKI9v4YtolMtdp8YqcvaMScXK94RB4KPWfs8TXiQoBNFH4ciBnK0zz0arNtmRza83TQFPOZqNvGEK5vIX/lFe1oTpkQhgfCsumRr7/Kza35OjuLC5iw7aiNO6pKd7rLTszjR8573KcKDMIrWgFwN9iA5EpUaISGBwZwLUv24vf32Fwcb/NUs4ds88AdHmOShufxtDDCEo3XwGdj7ga3wwLb5Rzg2N2rZOohteQLfx90ao9V/ivAgQAWr0Tbh6O22+8wRkTD8Hs9e3LZx+BEXDK7UwEZCimyoI9q3zY38WCOHUmzhYAcn0ZCQo7u3JyZ2Gggvl4PsZtynCA8SaRgXcwhRAyGbK9VUkQBh+KWGJRlbNRF7nsHP+WOHj/KK4iBmNU52+GhN98iX2Ll9iQJcMG3+EV7NGvHsKZoScw1Wb5spwqN4NUhvKgRbsiHFvp2+UEjMCYc98Lh7HHxrSCdHCcrH51m5S0SKqdx9XIshH7tm5/iKD/LQ3Nq0zMESJ9yPMqYIzzazZt5KDgKz+MJhnavHiHCIGa23xotqaMXCj9x6Y27JB98pwtua5BZ/SOetX+NYDHxp4ekj61iUr2xg4EsL72gfL0tyZwaGCe8cYs0WA5cMdBcevzkd6beny5LXyhEY6Co8iW59xB2htcfOoavwKBXR5b7POjYdK7tZDHQXHonzheo69Wa18N+Ms7vwRv486MXPd3o9v+hNtZy4s+KQw8jvKd/f30+Pj4+pUpvXdxUeDeJPQ70HTefU9c3nRwC/1js2eKPjqD4JrubPgbV1+pf19fX19PPnj9PHx0ctRJXdrsJrPe1EeK5C+79TZFfjJ1vdW3xafsa9No7+lguHPV4mMPTCgOkFKD563XcVXmtxpcaC60+BUbGuaUQuh1JNPo5erBym98k9Cw8bcmk9FHIx7N404UEQxVBU9MuHPj5IDrvcR3CpSWBxgugt9qeJjUU8L1JLUCkWtooX4VAHFzhbarJxwIli2bypmZjRRb520BuLJ19r03s+TXi2gVEDIIN1CcYXyrou2ek5ssUGTOFaG9YgWqeFz0e43EuxwEqdDnYdLD+ujSMMcDX3mC3PniPwbb9aMEs+U4RHIWpCrijITBWMSHQhBs0lHlso+4qn5tp95sSBcF1232KXYlkBWww7j0RiYzCviSPMVE3a5y7Oo7vnzAsv1wcbY8t8ivBosohmLlH4xCnYHvl+X88pcWrf/rwCpicaO+WRykVYpVgIJjdK/vLN2UmY2CISOOKeG5HgtBb5Wd5rhB1hXLM2RXg6gSALgrmsGFinWAa2zHOCyDUJDJ1C4KZwWC+JBqxcLGqQCMjZiwF8/FnX9Vlk8E8uDr6WQ16sVF0BdNWS5byGlyrQjNEU4dmiIMyKjtzsGiRjnxvY5Ab7anjKLhJKZFuKRe5g+ZrAUl3ksrUmMBQjJ9Kohto1cqzlpRYzZTdFeKnge63TwJIQ9srtf4k7RHh6c45IIifYjI+SI9Z+pJyGCI8CaXDpY2oPItZJtwfrlzGHCe8y1FpZDJwZWMI7c7FmExlYwptI9gp1ZuAPa5bd+Jke0qEAAAAASUVORK5CYII=[/img]

[br]Due rette sono parallele se e solo se sono paralleli i loro vettori direzione:[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAIIAAAAXCAYAAADHqJcNAAAFlklEQVRoBe2Y2UtdVxTG89c0TzUvNg/NU9M8NL5UzUNTA00DasxTDZhK0+hLFaFRoVFoNIKK4IRgo6IIzgMKjqgITuA8PSniFIdVfrtdh32vN3rNHbD1HNjsfc7dZw3f+tZa+9wb4l4uAiJyw0XBRQAEXCK4PDAIOEQ4PT2Vk5MTB5bj42PRZ0dHR2bt/BiCBbrRx8Xa1q/rEKh1Rf6LgAcRCASgK/AQQMlhBypQ9NCjQVdZtm7Vqb8xB1O/Lddd/4OAIYIdGF1DBgWfZ76CEyiIqktlc49eJSAz91z8dl2ujY0NWVxc9BgHBwchdd+jIhAQxv7+vmxvb5uZQDACDURra6vk5eXJ8vKyI0uJYBMAvbu7u3J4eOiQD5sC1R9KFG3fgqEHIpSUlEhTU5NkZPwm79//JbW1tfL0aaLk5+fJ5uZmMNR4yDBEAOitrS1ZXV01gRobG5Pc3FzJz8+X/v5+Q4pAAoFjjx//ILdvfyEjIyPGgA8fPhidKysrMj8/bwbrhoYGycrKMiCsr687FSIQ/R4eh+CmoqJCsrOzDXbBEg9mg4ODhgAa+PHxcent7TWDhAnm5VQElA0MDEh3d7fU19dLSkqKxMfHS01NjWAUZAnkio7+Vh49ipO5uTkjhlI3NTUlnZ2d0tXVZeaenh4pLCyUpKQkA+zk5KRoSfw/EEEzHdLYgyrpfbG3sbFRKisrnQqg5AAjX+94y7jMvUMEDfTa2powZmZmZHR0VGZnZ2VnZycgIuDA/fvfyPPnycYB7umBe3t7pgotLCyYdkCV4DkEYfC72hWMLxcF0s4mX88AkOxjn9qqhPQF7qtXv0pHR4dDWt7x3k/70NI+MTFxYf9HhjcRkNHW1hbaioCDLS0tcufOlyZgS0tL8vLlL8b46elpp0cDEH0rOfknn6Ovr+8MCLxz9+5XUlRUZDI+MjJSMjIyjFM8v3fvayH7y8vLpbi42ICfkBAvOTnZhpRKBl9B8PeZ9vHU1J+N3VQmfTY8PCwvXqQ4/ZdSj40Ql/3Y19zcfMYv1Z2YmGBa3ps3fxjZvjCALPjo76VESEtLk8zMTFNBnjz5UdLT04NeDbDJVAQOg2QjPRlAYmNjjNEYX11dbTKD3z+1PANsVFSUpKamSmlpqUepQ9+DB7Emo+yqAbgK/qfqVdDRb+vluZKTM5DeP3z4nQkoQeBMo+cZAvzuXaFjt8plZi8+nBcgJRyHP+3x9mxXKJWtRKA1MKgiVAg9L+i+YM1OawBsBsEnMO3t7fL69e+mRdjKAJAeZfc4e+2rdyHz5s3P5NatCEMG3UOmA3Jc3Pfy7FmSmdFdVVUlBQUFQlUKxgWpysrKDKFVHsGhVGuWAjxErKurM2XbJsJ5h0ElOQdhJa7q0FmrKKd/mwC6vogISgL7vKCygzU7RFCBBIZSSPZqwPQ3ZgDz/sa17717I+9wUNQyGxHxuQFb96k+AkXLOU+3bcdl1hDR+7OL4GgFUL8gAhUCH/0lglYLPo1JiI9hZsvzx3atCPrJrfehIsMZIijDP8Zuf5yw9+CAlnxKI2cCvh7IDjIBffQ+MpM1vZmsVKIgi+yNiYl2SrUt35+1vq+tSUutXdK1fBNItVntwC7OCvrFY+uE5DZ5cnJyfJZv5NPv8ZuD+EXJw34qAZ+QWjGwg/OM3SKGhoaE89TExLht1qXXZ4iAAZxMVfmlJXq9oK0EBwiut3x1mN/YS7n0pZustk/mXmouvEWPHrw0a+0ss30GcLKbcwXPtRWqD7Yy5Grf9vbN3sda9Wn10JbqLRcc+AMJwrIXO/RLAxLwjKQCJ3x5+/ZP4csrkOsMEQIRFqp3FRgFPFR6rrPc/wQRrnOAwuW7S4RwIX3F9bhEuOIBCpd5LhHChfQV1+MS4YoHKFzmuUQIF9JXXM/fkEC4PLl4jdMAAAAASUVORK5CYII=[/img][br]Possiamo scrivere:[br][math]\frac{l}{l_{^'}}=\frac{m}{m_{^'}}=\frac{n}{n_{^'}}[/math]

Due rette sono perpendicolari o ortogonali se e solo se sono perpendicolari i loro vettori direzione:[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOAAAAAYCAYAAADj7PGVAAAH10lEQVR4Ae1cW28TRxjlZ7T/oTzRIiH+AqhV+Q9BvUhN/wDioa36QKu+ACJvVVOVN6BECIQqKiRekCivlUpRYnsvTuK7d9f3U511jpksu17bcWK77EijuXyX+WbmnJ1Zw+YUsjSfFRgAnTawv+ehkG/AsgLkbR85p4Edt4acW0PeaWR55dagiZzjYYfZrmO/0kK7CwxGqOkDYJ4tnZrNLLM6tALcjZCAA5T2fFhWE67bgV1sw9oNYO01w2zvBsjy6q3Bjt0MCVhwm6g2eugNt/sAAhkBD3FhIY0DAnY7QKXcQtENYNstFJwAebeJXLGOfLEObmCWV20NPGxbDezYXnibKdc66PZP+AQcDN4cuAJ4vz88duNk1GF/nMzskw/5NGXqW5mSJ2AH4QlYKDRg2UFGwP/LA2e3hUIxQKHoDU/AwQkTsNvthjxg2el0RsRqtVpoNpuxHCGZRDDf90FbEYz1drs9suv1eiPZqHPVKgOAJ2B5P4Bj+0cm4PO//s5OyyUhcM71wyso3+cr9W74xvfmSDrmKyhJI/J4ngeR7uXLl9jf3wf7RCyTM7ILggCNRiPUI3mZarUanj59inK5HNqSqByDvlc2TUnAmxs/g1lEY/3K1e9C0rFke5muq4uM6cLFj0frtIg1WSgBSQoSJJfL4eHDh3jw4AEePXqEtbU1nD9/HtevX48lDm2Y9/b28OTJE9y9exePHz/G5uYmtra2sL6+jnPnzmFjYwOlUinkXRyRJyUk41tf/wrXrl3Ds2fPJjWbn94UBCTp1i5/gffffw/3tv4I85kzH4JAI8AoGwc0kXaczrxljGncuONkR4mFfrUuR/FDW/rig4Rz4bpP6m+hBCSJRAzVSZgbN26EZOIpFpd4MjLRliSuVqvhtZPtSqUSEu/OnTshsXkF5enIU3CWRPIRzCIf6+w70TQFAbnxBALjFAhYZ59Aov64cl6AjPOd1MfYkmTsP65Tap43AcaoNeYDb1ISLpSABLEIyDqBvbOzM3oXnPS0oZ38bG9vh2QjoZOIwv6kHCUWiWeS7uzZj8LTMKp3fO3he0C320e55MOxmwfvgC3kXR85txn+GspfRZUvXPwEBAHbz1/8MzwN7z8ZyaUXV9I2rt/so8+bt34Z+VedOvci45hts04fzKbfpDpjStMdF5Mp4xhmvHFjUn9cjtpQlxjR/IY3jvR1pJ+FE1DAJdk4iUuXPg27CHyCPS3xaki727dvh6q0py8SzCSO/FCelOkrmuRf/Yxpkrikf/SSBOyi2+2hXPIiBOQGesi7HgoO/2limDnvK1e/D9ss2ZYsrRwS8I2vqP69+3+G/tYufwnVCbjnL16BthyL/WabdepLppjYF/Uf1x4S8FWiruKQHsdh5rjjZHFjsY/x0VdSjtppPhyLMs01qhfXXhoCEqgEu8DNOkloptOnPwh/nFEfSSbiUpck5MLr5JQv6c9Skqz0qXQcBGTcnEt8mo6ABB3jJSi44SyHp2E8qahPuTJtVWcpPwKPqU/AEWzSu3lrcwR86gmI9CGZSMdx2Ce/0dKMIS0m2lKfhKFPjkcb+ZSMY0dl0jlKKZ+cM/1o3pP4XCoC6rpHIMadRq9f/xuLUZKCtjqtREYR0TSSHnWjmbJokk8RZFYC0j46ntryqTEOxzAdAQV0PY0JSoF+EkBQP02P4JZPgTsOeCIRZQIp41KMAmzaeIwpTZcxKfbonE0Z45Ze0riMj3pJOWpnzo0y+jcfAFF9s71UBNQJRmDGg/EwNNUyAcw6T604MlGfpByX5VOlYlI8XNgk37KZtmQ88v+27XQEJBgIfG0y42Wf2mnlJOCkTxHC9M9xRUyOY8pM4Auw8jFJTON0o4Q2x5WMJceJxhg3NsfigyIpR22oxzE1BtfQ3IOovtleKgISiJwIy2mSSTi9301jn6ZLUpN0jIv1ZLKkeZpFPh0BCXSuIUsCyaybG59UTyOg/NM+Cm6OReCZp5xAqThoRx/UkywpFvUzpnEEFKGpb87ZjEP2ioMy+Z9HyRjNNTf9f/b51/jm2x9ix1s6AvLEmTaZNqzPmyD0RwIyz9t3+lynIyBBrc0n6ASKSUGWRgrKpcPSPF3ZFtBNGfuoJxnrinGSuEy/cfr0RR3KNJb0KFOMkikO6cyrZAxc7+jcfvxpA7/+9vvyEzAdjO+ixnQEnBeYMj/xP1rNe12W6gR8F+mVPueMgPMG/TL5ywiYzoAFa/QxQA/tbgd7pRoKdhmW04Dl+IeuNHmXnydledXWwC12YdktWJaHWp3/M8z8IJAP38NfCE4DxuyD3GlWK0F3gD74mWar30GpWoVdLKPgVFCwGyhYPgpWG3mrPfyqWl9XZ+VKrAe/hncKHdi5AFauiXqljwE5N/ocIiNgAi1OrpsEJAXb/TZKtSqc3TJstwLbacB2vPDjXD5B+b9hsrx6a+BYLbhWgKLtw2sckC8j4MkRLH2kQXgF7fQ7KFcrcIv7sO0SbLsK26rDtvg3YprIO/y7MFletTVwbR+7jo9d10O91kX/0I0zOwHT+XHMGoPwTsKN6IdffLSCLgK/h8DvI/AQZt8HmsEgyyu4Bl5zEO6h1+ihw09W33oH5N7PlrJ3wNnWLd1Km2SUQ4oO/4ZWVl+ddRgRztjLdABMppERcLJ1StcyNyepnu4l01jGFeB+HlP6D7y7dPYn2BL7AAAAAElFTkSuQmCC[/img]

[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAd4AAABWCAYAAABhCvfCAAAdlklEQVR4Ae2dW68mVbWG/RnyP7beba8w2Xqx3TRcmPgXjHiB4Wq7jcG00HghidwZY7bQxhhaA2g3GuXQomLEw1ZjBPsgajdRoGmO3Rxq5yn7WRk9qapV32kd35kUc84xx3jHGG/VnOOrby16va9LCwNhIAyEgTAQBnaMgfftmKc4CgNhIAyEgTAQBroU3jwEYSAMhIEwEAZ2kIEU3h0kO67CQBgIA2EgDKTw5hkIA2EgDISBMLCDDKTw7iDZcRUGwkAYCANhIIU3z0AYCANhIAyEgR1kIIV3B8mOqzAQBsJAGAgDKbx5BnaNgXfffbf3bf/OO+90jt9+++1diyuOw8B+YoA9w36hd7yf4j+MsabwHsa7vss5czhQZGkeFm1IrrfyzMNAGBhmwA+u7Km0vc1ACu/evj8HPrr2kOCT+9WrV/tP8Ac++SQYBtbAAHvmypUrPRL76a233loDaiA2yUAK7ybZDfYoA/VN9/Lly91LL720VWzbYjwKkoUwEAZ6Btgz7KFLly5t/bimUvOXv/ylTnd0vJu+dzTRBZyNFl7I8qp4Q7K6nvHhZIDn4u677+5+8pOfzCKAT+j/+Mc/uhdffLF79NFHuzvuuKP79re/3V24cKE/OPwE/81vfnMWXqtEHDfffGR2PEP25JR28Bnw2eV52eut/d0HP7Q+//zz3eOPP94dO3ase+ihh/p9RTFGn73gvjTXZffVMvzgcyf9LRPjTttMFl4eRC4PIG9ala0SMHj74WFfJUds5a8dr4q71+w//elbtzb4VGwcBs8880x3/Pjx7v777+/uvffe7sYbb+xuu+227sknn+zeeOON/mfA9cCYwhtbu+GG948tzZLzQaLeu1lGe0Rpv8YtfTsdP8/aBz/4Ad33HyK3JisM2BObyIU9xD5hH1HU2Etf+MIXuo9+9KPd7bff3j3xxBPdm2++2fu+6667rstgN87c/byXriNvTZPRwgs+N6j9pMJDBInrapt4KNcV2zpw2o1XN/c68PcSxtzCyy+B8HNc23PPPde//fppnk/q6KzCFc/VKvbExmG8zmfdfDfdk3s9XPdbHu1zVHPZFHft87JXzyX2BlfbkLGPzp492xdc1inMd955Z6u68r54D+BMAfc17V8MLFx4MfMwYkO7Segp0u0Dy9w17Biro703Azk64iMHk0tdelvVr3LX7auesopb48G3vtBpW7tGPsYLDjbOGXP4mzNy5vT6VJ9eGb062NrEH8oVe+T0+mvtwKy2zPWvv9ozptEPYSJXBz10Kv5YvBbWc+fO9V+NUXDPnDnTj8FhvcXuA7n27YE50o818yKGNq4hGzmv+aDH/WJtqGnTxoEcmXJjAQN+jIcefxWfOXJtq1/9iaGd/uQeDJ+zn//851vPoLmJ47z6cDykY0740bex2A/FXXMSlxxpzCs/jCm0XOryzUWNFV/Mq0xd42Be8ZEPNeT6hDNaxai4+DM/5DVubdDx/imjt2HDhcwYGWOnvj600Zc4Fl4+vHLxIZW3Wn6pir109OjRXnb+/Pn+3vPmawNruw8y8opuOzYG8Wpf9c2lrsMLOkNNLis+vuVFm6oHXtVHB1lro+1e6lcqvJDoBicpbmj70FQyvDFsJMaQ5teBzL0x4EgoJOKDOZebQ3/YaTvk25uAjuvIuGh1zDr49PrCrjbmxoOcmG2OKya6YmirftXDpxsCPXhBxkWTmxZDLNblrWKxLmfYqsMYm5qvfolLXcZwQW9+rKnjvTRGdGnEwBhd/fcL1/7DYXH69Ok+T3q+KvvAB/6toxhzePBJXSztjIM5sciNvKlHb7zoVD6GdGs+rU/8tDLwkSkf0sE/l61ywFj+ah7ijHGGHL6rTeUZOTrEVfOssbCOHs1nwRjt0QcDXTmuGMjEYOyzig25Ydc25PJl7uhUHMdtXJU7/JkbflxjTBxgGzO9eYhd42IdfRrjisUYTC78YS9ejRt7fJiTcdDTai7o6K+O9Q0Ol771YxzG5zdD7CGKMHvnyJGbelvW8MmbLz/GufXWT2390iJ41W/10wd77blGThzEZfzYyYF5aWOPjvrm4Ro9eFxtw045Yxo4Vaac3vjwUc8ffWNfY634re/dmi9VeCWEoOvNI0EJqgm1iWMjBsTV5oPuOuTWTaM/1qstehDftmrrWmvnzcM3+DZswW0b+YhrvsSDf+Y1X+MFo8XHb8WvujVGbMXGjz5rXK1ce+TGij62zo214tT8ax7eF3QZ26NvDpUv5Noj16b6YlztjRl53UTa1NgYi2mvnvbkTqt5jukOybEldnF6sGv/qfej5q1Oez9q7DW39v5gTyxVX0z6mrfzlud2L9T8xcIHcQzlVu+D+si8z8iYy1nVH+OLGFij6ZNeHs2B9coP88oFY+1Zq3HN4QYbW4275bxitTkxN176yov56ANd16s/ZMzx2/qu+YtHzvgaa/oBSz16x9oxNx5lbV/9w4P6lRP8tA09bduc0CUH4mwbdtVPaysudnXM3JhaG5+t1tdemU8WXm5SSxQJcdlMnPnQjVbe2mhfH0Z8oQeO+hBdY9CfN0sc9CsW8vYmIeMG+cBrq1178/ALRtvUwydj2piu8aKjnXisVXzicG5MQ3ba117elGkPl2wGG3ryOXS/iMlW7wOxi+PY3pjloM1TvLavsdQxem5gbeo6/szP9bZv8yCmsTaFRRz4btuUDbo1XuY1nppb1SMv1qb4A6fmUnGNURzn7X3mPuG33l91sR3CbP2SP7q0yoXY4tUeDGyMH11iaFvlh7UajxjaMPf+MBa7tVO/9sStPn3rx7U2pzY+MVvekWNrztUfa/LW+ha/letnqIdH/FQ+vcdVH+ypNvQ8ql/5UVZ7fOu/jtUZkrlG7OCjw7hyVXlgrebgPZ+y0cde6icLr2T4ABI4D1JtlaAxYpG7OcCqGNpXQisO8iF9cLBlnVYfGONTBzyaeXCzajw+UKw7Rt9NI17tufniIgfPhwAc41KGzhC+GO0audlcq7qu2bPW8sSatuqhIw69Y9fb/F0Hxwe+2qFvrmDLK/JqK37tqz526OOHVteYu44v9FhnbFzaocvYPNRXjt2YLnJzQZ9GzlX/mriX1/xaHXDki3G9n8j1Q17EpC/lxq8/e+TVF1htHGBUe9bVYc24qlx8sLFVX1+tn4pfc2vvm7j0rOmbObmbD37MHR3WbOqIIV/M8W2MVY+1Nmbx7NEnT+y5mNsqbpsTNuZR48bGHOSv2oJvXtVfHeMfbHCUi8V8rKHT5g9G5QpbdMRmrcWs8RKrvhmzpi0xtrZygh/szNWYkYmnTF1682VsnK6LjX/H6hlHzb/6Yl0dbPZCmyy8BCjhkF7JcA0S0CExkkWvbcixZa0Sj121Z4weOoxPnDixhQm+pHtDkYlZcat/bWrs2IGPDRc6NP1WX1O4xoEtNuiapzEgI0bWqw98IjN+sIyj8iIOuvKjXl2rfrTXJ/r6MR99IxePHh/0dZ0xmOq6BhaXNnJKXOiMxWvcrNuMz7kx17l+jNM1bImvNnSH5OZQdc1Bbuoa93Oo1fyG7LAhBtaIl0OZGI0dORj0xMRYjpXR16ZtzbXGoVyZuNrRs4a87jPktWmPTotJTMi0YUye2GgH/lDDRjzW0QcPey6bMn2Ah0wfjJFxqUMPRouPrOahD/2zBg529uakTzBYw792xoicZkzYMuYyJsbageV6L9zm3JFT4jRX7WqvvypjbHyMwWIuDjaVL3SIzzwrJjYVi3G1FVv/4NR1sV2vPX7EMzZ6MVin4YOxMVYd1utcG+SMzakH2gP/2bbwriNGEm9vwjpwg3GwGXCDTWXpZpzSca09HJSP9Ty3dQOP6UUeBvYqA1NFh2K3TEFaZM/Jy6J7T7uD2qfwHtQ7ewDyYrP6CXgsnUUOjkV1KfxpYWC/M7DuD4+L7CO5q2/Lyg5zv/HC6+v/sp+uDvPNSe7/+vpoN3jYruDvRkzxGQaWYYBCuZvfOOI/++n6O7fxwnu9u8zCQBgIA2EgDBxuBlJ4D/f9T/ZhIAyEgTCwwwyk8O4w4XEXBsJAGAgDh5uBFN7Dff+TfRgIA2EgDOwwAym8O0x43IWBMBAGwsDhZiCF93Df/2QfBsJAGAgDO8xACu8OEx53YSAMhIEwcLgZSOEduf/+yS3/dixz/t6lc8bqAMHYP9c1Arkl1o7eVsfIKla7pk36MBAGwkAY2H8MpPBO3DOKLAXQwsecgssflr506VJvaSGm55rT1LX3D1i/9tprHRcNmW0urvrpw0AYCANhYO8ysKcLL//aCf/iiv/qCv3UPz2m/jr+iTSKnQWX2/fqq692Fy5c6F5++eXut7/9bfe1r32te+yxx7oXX3yxv7voVn1v+dA/r1aL+dWrV7vLly/3hfxXv/pV9/Wvf73/A/H48a133YUXHlfhCJ65D94Xc00fBsJAGAgD2zOw5wsvf9XFYkvPfKxR5PgrHv4bu8z9qzBjNlPy+kZ68eLF7uTJk/1fTPrWt77VHTlypPvEJz7RPfLII93rr78++rZr7NWPhZRC/cwzz3QPPfRQ9+CDD3Zf/epXuw9/+MPdJz/5ye6Xv/xlR1GmGUfFWGVM4ZSjIZyhDwutHvbgrKutE2vVmLhnfDDJB4tVmYx9GAgDQwzs6cJLwLXwchhOFV70KQi1qKzyZlcLHm+fFMIrV650FOHTp093zz777NZXwlW3Ej1UeCm4Fl96vlYG+8yZM93Pfvaz7vz58/3X2UNv0BV72TGcTPEyFHPriw8462xzfK7T3xgWvFhwiWnOh5AxrMjDQBgIA0MMrFx4eVPhoPLi4KqHFeN6mBEENurZI2dc58i2K7z4xcZWC6+xDb1NDcWlrMYvLj3FF18USX7Oe+zYsetyrbqO5xYUsCzAx48f13zl3pwqr4yHONHZdjGD6Ycb+BcLOXNaO673SD+1386nmOBUH9W344pLHMiHLtbaVj/Y4WdOXC1G5mEgDISBKQYmCy8/v/zxj388Zd8faBxWvAFxKNIz9+DlgGaMjMOPMYcZc9aUM/agq29TrHv4gc/chg2YrDOm0TsGD30Pau3osTEW5uCAr4y+bffdd1+f37lz5zqKI36G9KqdsVdZOya+I0du6mNgjfHZs2dbtYXn5AQ2McKpscrPGOB2McOTF/jiMcZWv/iU13pPh/xu5xMcdMjBnPDL2FiGMFgfu+TDeOTJOT7NjTXHrqcPA2EgDCzDwGjhfeGFF/qiReG6554vT2IPFUcOOw4uGocWOhyQNNaYu66MnsOTNQ/FIWz0wHKNA9GDnbEHpH7xVxty9Kscvx7g2NfYtOVrYXxSdPkaWJ+uD/VDxWBMj6+vweXtt23EPHQZ85C+PLBWY61j7YjTi3XH9PitDZ/IafDkGD6xRYZN5bHGgh3r1Yf3Uln1xxj7Ng50iYWG73o/W/s5c/CJw0YelavWv3rpw0AYCAOLMDBaeE+dOtkfQhxEN930X5OYHpoocVgxp/fgUlYPSXTqQcYahxx9XavYruGHQ7ceigbIAe0h70E6dCAbGzg0/GzXfMtVTz/Oh3rxh9aqjGJLTMbqz4DVQU7+7UUMFjt16dETi7FxwInjql/H263XvI0He+yY0/AtTh1XP3WsbpU5JubqU3nNG/v6PKlj7qy3F3y3DUxxiHvIb2uTeRgIA2FgEQZGCy8gn/3sf3cf+tC/d08//fQkZlscLYgWBYzRqYcycw+4Wpg57FjzUGyxtVMPTHDExqeHJXL00a3Nuev02IjBnKttrGtLP3bYVzt05jSw0TXvOTboGE+rDxZr5FHH+OGa8rNdzHBKkzd916KlT9YcD3Gq7ZRPYq33VJxq43Mh3rI9fsSXK7CQMXdtWfzYhYEwEAYmC+9cejj0uDgI62HIwY+cw4xDmd5DVH19YIcOh5s2jpGfOHGiX2fNglLXweViXR0wGdeCgD9jAAcMGgcqelw1B+OjR+7Bi53FoOqohy6XeM61b22IhWtdDSz5xrexEjfzqSYnYzpggdHGS662OjZ314b6KZ/eG3TUw7d5sG6uQ9iLyMSq+Nrjo83ZtfRhIAyEgbkMrK3wcgiOFZW5wSyjt6zPZe2WiXGOzbrjWTfedjls2t+m8dv8hvxZ6FvdzMNAGAgDizCw1sK7iOPohoH9xACFeKgY76ccEmsYCAN7g4GVCy9fvfnVI1/hpoWBMBAGwkAYCAPjDKxceMehsxIGwkAYCANhIAy0DKTwtoxkHgbCQBgIA2Fggwyk8G6Q3ECHgTAQBsJAGGgZSOFtGck8DISBMBAGwsAGGUjh3SC5gQ4DYSAMhIEw0DKQwtsyknkYCANhIAyEgQ0ykMK7QXIDHQbCQBgIA2GgZSCFt2Uk8zAQBsJAGAgDG2QghXeD5AY6DISBMBAGwkDLQApvy0jmB4qB/DOPB+p2JpkwcCAYSOE9ELcxSbQM+JeqWnnmYSAMhIHdZiCFd7fvQPxvhAHedOufJtyIk4CGgTAQBpZgIIV3CdJisvcZ4I03f8Zv79+nRBgGDiMDKbz76K6/8847W9G+/fbb3bvvvttfCBkv0tBv8bB/6623Fsaa65e/ZOVfs9r0H5S/++67Oy4K8E79AXvesvGJv/ylrrlPRfTCwOFjIIV3H91zC6VFlyJJo3/jjTf6Xp2ptGrBBuvVV1/tL2yYX716tbt06dIUxMJrFFqLEW+im/6lJ4ofRRA/+Ga86eYb9qZz23QewQ8DYWCzDKTwbpbfjaD7dkuR5KLYKpvrELvXXnute/3117s333yzu3z5cvfKK6/0BRw8Cu+imFO+689b63jKZpW1G254/1ahp+huuvBS3C28q8Qd2zAQBg4+Awe68PKGta63HbA4WH1rW/TRWMdbkIWS/sKFC90DDzzQHT9+vPv973/fF8+hQvnUU091v/vd/22F+/TTT3fIKLzoc/3zn//sC+6vf/3r7t577+2+973v9UXZN2r1tkAWHNSiRAHkbXSTDa5rcd+0P3Lh2SDPRduyzxN+Kq+L+t2E/jK5LMPZJmIPZhjYSQYOdOH1APYQZs6b0DKbHRtsl3lz4uBfx9vQlStXOgrnd7/73e7kyZPdl770pe7GG2/sjh071hdii2l9gIiZwmr73Of+p/vzn//cF1y+Uv773//e/ehHP+pOnDjRPfjgg93HP/7x7pZbbum+853v9MUcu2XeqPVHD2cWJg5n+FjmkK6YU2Owuefcb3xv0pdxmCM+5z5fqz4T+NqJDxXmuF0/tTe4B6xzEbcN+U7cH/2lDwN7gYEDXXghmIPJwsu83fhzbwKHxbKFl4N4XYcLXwvT+Fr4ySef7N92Kchjb6XEXFs7d42izVv0D3/4w+6FF1647hev1JnTE4fNX9Q6d+5c/+GAAn769Ol+bLz4Rb6OBhYNPL4J4AMJvpm3lx9SiIM458SALh9W2tixNUd8tr7Alwviw55nYqpQzeFjHRhz/MzRmXrG2Tt1D7Ina/Ft53P8RScM7GcGVi68fpJl43kQ1E3FWDlEMefAcaMyXhQDHDGx5c2hLWysI2fDu+nR0a83zXjQNW71qoy1tvASOzpg1tzMSXtj1ac9mMap74qjXtujS4wc4GJw2DOvjcLMV8c2vpL+4hePOr2uv+uuu3osMMA+e/bsdevLTvhavC1Exmq89I71Qwxjlzr0FEKbGEP+Whm/UMYvpFmswZDXIb/1/oDFByAwWtyhufnxAcnmM+mcnmeBq/pizPM01HzOhtaQmQ9jcgJbueNeMPAfbI0DP9vp86yPNWzrOoWWeGxz8NVNHwYOAgOThfevf/1r9/DDD0/myQaiIHGQsMHombvpfcNis1mIGHOh6yZkvAhG1RfLQJl7WKnHGvHV4kns6BIr+vTqoE+82KPHWrXFDl3s0GGdy1iQie3Y+OzlAzsPIg8o5o7Vp+fN6siRm7pbb/1U758YGHu4W3zQ/fznP9/96U9/2jK/554vd7/4xVNbcwfywFsihYO3NnDnNGKvDf8UM4rS3/72t+7ixYt9z9iL54rxc8891zHmF7tq3GDif+iSJ33iC07EotfPVH/mzJnupZde2iqc+Ad7yCcy1tCxsPLLZ2CYy5Qv8uEDCI14z58/3z8z5kDPc4SP+izw/NCQO642QzLXwWGdZ8icGJsjz+RY0xY74vKq+sro9aMM+9qUKzMm58Q09Ky7nj4MHDQGRgsvXztSaLg4iKcaOm4cNhlzNi0yNjgye3DYqO3GZ74sBr7wyYbXP5u59cU6eujQjLOfXPsPcXiggaF+a4tPGjHrmzm2zGtDJmaVY8vlQeUBRHxc+tCGQ5+vLLXjAL///vu3eKMw1ALWxvGxj/2nUO/p8YVPCoP8VCViHLq0MwfsKTIU/O9///vdqVOn+q+v+Qrb65FHHunXmP/gBz/ofvOb3/R5VX9zxxS8xx57rMcGC2z9TPWPPvpo9+yzz279Ulrlbcy3/PLmyjcCjz/++CxffPPw/PPP97Dww9ft7fMA58jkEWXuM3Ku9llgvd1DbdzY+HwxRp9nTHmrX+c+Y8gYD/lXv81FuT3xg2FjjMxGTNthqJs+DBwEBkYLL4cWBzfXLbfcPJkrOm4sixU9G33ocGCTtRsNvSEM9MYwlHMoEAOHFhuasQdFtWedNXSMsx4AJMm6salPXI7Vp8d/9Y199SdpyMRURm+84BAPmOJXvXYM1hNPPNG/fREbMfgmpu4f//jH7o477nDaXbx4ofvMZ27bmreD++67r/cNFrHUr3DRRcZae1UeWkxiotDUhj1519YWPdbJa+yqtvVnp1W+3ZjYLKTqkuOYz3pftANjmUbBHnoeKpeMq8/Wjxy18jonF3KiMYZ7mvewn4z8x/3EMs9ne8+Mj55c6ryFxB/+begbFzKwh/hQP30YOGgMjBZeEj169Gj3kY/8R/eHP/xhMm82qRvLjYgBm8lCx+ZysyFvNxqbewgD2RgGNjR8elCwyY3HDa0e84rFmDXiMj7iUl8s11tbYqs65qx9H9w1Htp8Wav5MsYPtsRCky9x7InDZvzO7b/yla90P/3pT5123/jG/3anTp3cmrcDfBlDuzY1H4txyIa8xuId0j+oMnhonweeI5oFrH0WfCbkRD3k6DJvW/uciFHvM37be8jcZxNMcLRtfVS9ds05tuQrRrs/zEX9EycecJg+DBxIBiYL79yM2ZhcbK66Ed1wrLnZkDFG18MGP8jmYHAocKHPBR4+GYvHRnadXl/qMaeBwxi/xm3M2CHzQBNTW+bY2SOvuWlXY2VcGzpc+MGWxtyYW33WydFYmaM7pEdstTFv3z7rOhjGXOXrHrdxrRt/v+Bx37znxMw99XlTPvUs+Nxgi359JpANPSdyw7Pqvea+D9m6l8BGf+gZM25xp3r8cQ1hIdcfX//zjPDjh7QwcFAZWFvhbTfvooRZ6Ba1i/57GeCXlepvM6PRzt9rtXkJhzj3eZONAsHhTuMw159yi9q6Y6B4uAfojWHMTy02Yzpz5UOFd64tvBDLMo0818Fny9XLL7+8TDixCQP7hoE9U3j5lOvBtW/YS6ALMbDKIT/XEYWAg9xiQuHFLxfjdRSKNhYw8edlDK1eO19X4SK3ZdsqfPiWuqxv7OBslfhX8R3bMLBbDKxceNk4HHRcy24gNvCqGLtFYPzOZ8DCNN9icU2eJT7EWVAsvCBt8mtucvOD4yJ5rqN4Lc7S3rDgHi17ZuyNDBJFGFiOgZUL73JuY3UYGVjlw9lcvih+FjN6i2Edz8VaRI/cbBTeFBTZSB8GwkDLQApvy0jmG2PAn7duzEHzv77UIuwbqW/C64wBzJobY4v/Ov0EKwyEgYPBQArvwbiPez4LihNf9VIAN9kqPsXPQst4U2+h+KjYFHz9bjLXYIeBMLA/GUjh3Z/3bV9GXYvTvkwgQYeBMBAG1sBACu8aSAxEGAgDYSAMhIG5DKTwzmUqemEgDISBMBAG1sBACu8aSAxEGAgDYSAMhIG5DKTwzmUqemEgDISBMBAG1sBACu8aSAxEGAgDYSAMhIG5DKTwzmUqemEgDISBMBAG1sBACu8aSAxEGAgDYSAMhIG5DKTwzmUqemEgDISBMBAG1sBACu8aSAxEGAgDYSAMhIG5DPw/6kvvBag5CmIAAAAASUVORK5CYII=[/img]

Una superficie sferica di centro C (x[sub]0[/sub];y[sub]0[/sub];z[sub]0[/sub]) e raggio r ha equazione:[br][math]\left(x-x_0\right)^2+\left(y-y_0\right)^2+\left(z-z_0\right)^2=r^2[/math][br]Sviluppando i calcoli, abbiamo l'equazione:[br][math]x^2+y^2+z^2+ax+by+cz+d=0[/math]

Possiamo scrivere le seguenti relazioni:[br][math]x_0=-\frac{a}{2},y_0=-\frac{b}{2},z_0=-\frac{c}{2},r^2=\frac{a^2}{4}+\frac{b^2}{4}+\frac{c^2}{4}-d[/math][br]Pertanto, l'equazione rappresenta una superficie sferica soltanto se i suoi coefficienti soddisfano l'equazione:[br][math]r^2\ge0\Longrightarrow\frac{a^2}{4}+\frac{b^2}{4}+\frac{c^2}{4}-d\ge0[/math][br]In questo caso le coordinate del centro e il raggio sono:[br][math]C\left(-\frac{a}{2};-\frac{b}{2};-\frac{c}{2}\right)[/math][br][math]r=\sqrt{\frac{a^2}{4}+\frac{b^2}{4}+\frac{c^2}{4}-d}[/math]