Drawing Angles Game
Drawing Angles Game
Table of Contents
- Setting the Stage
- Setting the Stage for the Game
- Setting the Stage Part 2
- Setting the Stage Part 3
- Random Angle
- Random Angle
- Setting up for the Animation
- Setting up for the Animation Part 2
- Correct Answer and Margin of Error
- Correct Answer and Margin of Error
- Margin of Error Part 1
- Margin of Error Part 2
- Margin of Error Part 3
- Margin of Error Part 4
- Margin of Error Part 5
- Margin of Error Part 6
- Checking the Answer
- Checking the Position of the Guess Using Error Margins
- Checking the Answer with a Button
- Checking the Answer with a Button Part 2
- Checking the Answer with Button Part 3
- Checking the Answer with Button Part 4
- Scoring
- Scoring
- Scoring Part 2
- Scoring Part 3
Setting the Stage for the Game
First, we need to construct protractor shape to measure angles. So, we need two half circles (using circular sector [icon]/images/ggb/toolbar/mode_circlesector3.png[/icon]).
Now we have two semi circles. If the smaller one is pure white, then it would look like the shape looks like protractor. So we can have arrows (line segments) to measure angles. Now, create the two semicircles either using toolbar or command (CircularSector).
Random Angle
It is time to create the random angle for the question. There are several ways of doing it. The simple way is creating a slider between 0[math]^\circ[/math] and 180[math]^\circ[/math] and then hide the slider from the screen. [br][br]When a slider is created, GeoGebra automatically defines a variable for it. We will use that variable to show thr angle on our construction. [br][br][math]\alpha[/math] is the slider variable. We will later change the [math]\alpha[/math] randomly with a button to generate new questions. A' is the rotation of A around O with [math]\alpha[/math] degrees.
It is your turn to try.
Let's add a button to change the value of [math]\alpha[/math] randomly. It will be the first time, we will write our command to a button. We will use two commands to achieve this:[br][br][list=1][*]SetValue()[/*][*]RandomBetween()[/*][/list][br]SetValue, as the name indicates, sets a value for the variable stated. RandomBetween command produces a random number between the numbers given. Do not forget we need to generate angle, so we shouls a [math]^\circ[/math] at the end of the number.
Your turn.
Correct Answer and Margin of Error
Because users will guess a random angle, we may not expect them to guess the angle but accept answers within a margin of error. We might categorize different margin of errors as more precise and less precise. This will be our design decision.
How would you score users' answers correct, partially correct, or incorrect?
Checking the Position of the Guess Using Error Margins
Now that the error margins have been set, it’s time to evaluate whether a given guess falls within the [b]first margin of error (n)[/b], the [b]second margin of error (m)[/b], or [b]outside of these regions[/b]. To achieve this, we will use the [b]IsInRegion(point, region)[/b] command to determine the position of the guessed point in relation to the error boundaries.[br][br][br][b]Step-by-Step Implementation:[/b][br][br]1. [b]Regions Defined by Error Margins[/b]:[br][list][*][b]Green Region (n)[/b]: The tighter, more precise margin of error.[br][/*][*][b]Orange Region (m)[/b]: The broader, less precise margin of error, encompassing the green region.[br][/*][*][b]Red Region[/b]: Outside both margins (purely decorative but indicates guesses that are too far off).[/*][/list][br]2. [b]Using the IsInRegion Command[/b]:[list][*]We will use the [b]IsInRegion(point, region)[/b] command to verify if the guessed point lies within a specific margin.[br][/*][*]The [b]point[/b] represents the guessed angle’s position after rotation.[br][/*][*]The [b]region[/b] corresponds to the defined circular areas:[br][/*][*][b]Green Region[/b] for the first margin (n).[br][/*][*][b]Orange Region[/b] for the second margin (m).[br][/*][/list]3. [b]Checking the Guess[/b]:[br][list][*]The logic will follow these steps:[/*][/list] 1. [b]Check the Green Region[/b]:[br] • If IsInRegion(guess, green_region) == true:[br] • The guess is [b]within the first (n) margin[/b], indicating high precision.[br][br] 2. [b]Check the Orange Region[/b] (if not in the green region):[br] • Else If IsInRegion(guess, orange_region) == true:[br] • The guess is [b]within the second (m) margin[/b], meaning it is less precise but still acceptable.[br][br] 3. [b]Outside Both Regions[/b]:[br] • Else:[br] • The guess is [b]outside both margins[/b], indicating it is far off the correct angle.[br][br] 4. [b]Handling the Results[/b]:[br] • Depending on where the guess falls, you can provide different feedback to the user:[br] • [b]In the Green Region[/b]: “Excellent! Your guess is very precise.”[br] • [b]In the Orange Region[/b]: “Good attempt! Your guess is close but could be more precise.”[br] • [b]Outside Both Regions[/b]: “Try again! Your guess is too far off.”[br][br] 5. [b]Visual Feedback[/b]:[br] • Use [b]color-coded highlights[/b] or animations to show where the guess landed relative to the margins (e.g., flash the corresponding region or mark the guess point).
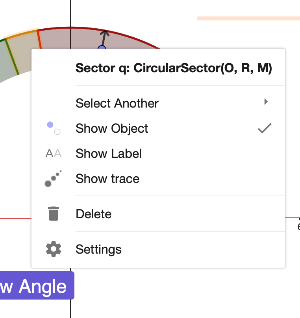
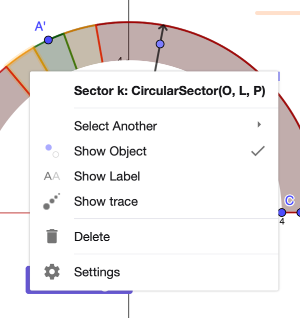
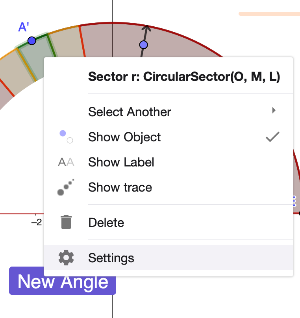
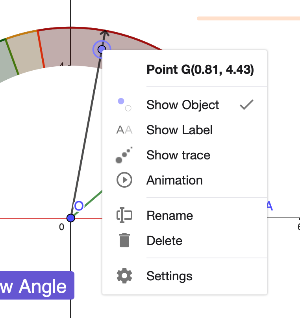
If you are do not know the label of the point (for guessing the angle) and margin of error regions, you can right click on them and see the names (like in the examples above).
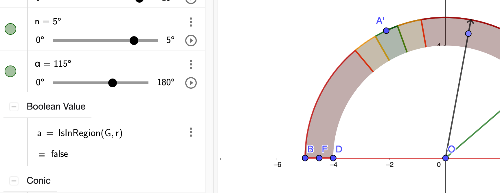
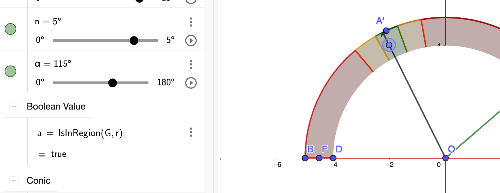
In the figures above, we observe how the [b]IsInRegion()[/b] command works to verify whether the guessed point falls within a defined error margin. Specifically:[br][br][list][*][b]Green Region (n)[/b]: If the guessed point lies within this region, the boolean variable a becomes [b]true[/b], indicating that the guess is [b]precise[/b].[br][/*][*][b]Outside Green Region[/b]: If the point lies [b]outside[/b] the green region, a becomes [b]false[/b], showing that the guess is not precise enough.[br][/*][/list][br]Now, it’s your turn to [b]apply your skills[/b] and extend this logic to incorporate multiple regions and provide feedback based on the guess’s position.[br]
Scoring
Now, let's score the questions. For now, let's give 3 points for the correct answers, 1 point for partially correct answers, and no points for incorrect ones. [br]We need to store scores in a new variable.
Scoring works. However, there is a problem with the scoring. First, let's create this and then solve the problem.