Side-Angle-Side Triangle Congruence: IM Geo.2.6
1. Geo.2.6 Lesson
1. IM Geo.2.6 Lesson: Side-Angle-Side Triangle Congruence
2. Geo.2.6 Practice
1. IM Geo.2.6 Practice: Side-Angle-Side Triangle Congruence

0

Side-Angle-Side Triangle Congruence: IM Geo.2.6

GeoGebra Classroom Activities, Dec 2, 2020

[url=https://im.kendallhunt.com/HS/teachers/2/2/6/preparation.html]“Side-Angle-Side Triangle Congruence”[/url] from IM Geometry © 2019 [url=https://www.illustrativemathematics.org/]Illustrative Mathematics[/url]. Licensed under the [url=https://creativecommons.org/licenses/by/4.0/]Creative Commons Attribution 4.0[/url] license.

Geo.2.6 Lesson
1. IM Geo.2.6 Lesson: Side-Angle-Side Triangle Congruence
Geo.2.6 Practice
1. IM Geo.2.6 Practice: Side-Angle-Side Triangle Congruence

1.

Geo.2.6 Lesson

1. IM Geo.2.6 Lesson: Side-Angle-Side Triangle Congruence

1.1.

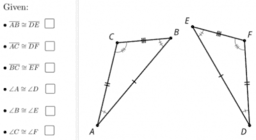
IM Geo.2.6 Lesson: Side-Angle-Side Triangle Congruence

Checkmark each piece of given information that is used in the proof, and each line in the proof where that piece of information is used.

Proof:

[list=1][*]Segments [math]AB[/math] and [math]DE[/math] are the same length so they are congruent. Therefore, there is a rigid motion that takes [math]AB[/math] to [math]DE[/math].[br][/*][*]Apply that rigid motion to triangle [math]ABC[/math]. The image of [math]A[/math] will coincide with [math]D[/math], and the image of [math]B[/math] will coincide with [math]E[/math].[br][/*][*]We cannot be sure that the image of [math]C[/math] coincides with [math]F[/math] yet. If necessary, reflect the image of triangle [math]ABC[/math] across [math]DE[/math] to be sure the image of [math]C[/math], which we will call[math]C'[/math], is on the same side of [math]DE[/math] as [math]F[/math]. (This reflection does not change the image of [math]A[/math] or [math]B[/math].)[br][/*][*]We know the image of angle [math]A[/math] is congruent to angle [math]D[/math] because rigid motions don’t change the size of angles.[/*][*][math]C'[/math] must be on ray [math]DF[/math] since both [math]C'[/math] and [math]F[/math] are on the same side of [math]DE[/math], and make the same angle with it at [math]D[/math].[br][/*][*]Segment [math]DC'[/math] is the image of [math]AC[/math] and rigid motions preserve distance, so they must have the same length.[br][/*][*]We also know [math]AC[/math] has the same length as [math]DF[/math]. So [math]DC'[/math] and [math]DF[/math] must be the same length.[br][/*][*]Since [math]C'[/math] and [math]F[/math] are the same distance along the same ray from [math]D[/math], they have to be in the same place.[br][/*][*]We have shown that a rigid motion takes [math]A[/math] to [math]D[/math],[math]B[/math] to [math]E[/math], and [math]C[/math] to [math]F[/math]; therefore, triangle [math]ABC[/math] is congruent to triangle [math]DEF[/math].[br][/*][/list]

Two triangles have 2 pairs of corresponding sides congruent, and the corresponding angles between those sides are congruent.

[size=150]Sketch 2 triangles that fit this description and label them [math]LMN[/math] and [math]PQR[/math], so that:[/size][list][*]Segment [math]LM[/math] is congruent to segment [math]PQ[/math][/*][*]Segment [math]LN[/math] is congruent to segment [math]PR[/math][/*][*]Angle [math]L[/math] is congruent to angle [math]P[/math][/*][/list][br][size=150]Use a sequence of rigid motions to take [math]LMN[/math] onto [math]PQR[/math]. For each step, explain how you know that one or more vertices will line up.[/size][br]

Look back at the congruent triangle proofs you’ve read and written. Do you have enough information here to use a proof that is like one you saw earlier?

Use one of those proofs to guide you in writing a proof for this situation.

It follows from the Side-Angle-Side Triangle Congruence Theorem that if the lengths of 2 sides of a triangle are known, and the measure of the angle between those 2 sides is known, there can only be one possible length for the third side.

[size=150]Suppose a triangle has sides of lengths of 5 cm and 12 cm.[/size][br][br]What is the longest the third side could be?

What is the shortest it could be?

How long would the third side be if the angle between the two sides measured 90 degrees?[br]

Mai and Kiran want to prove that in an isosceles triangle, the 2 base angles are congruent. Finish the proof that they started.

2.

Geo.2.6 Practice

1. IM Geo.2.6 Practice: Side-Angle-Side Triangle Congruence

0

Side-Angle-Side Triangle Congruence: IM Geo.2.6

Table of Contents

1.

Geo.2.6 Lesson

1.1.

IM Geo.2.6 Lesson: Side-Angle-Side Triangle Congruence

Checkmark each piece of given information that is used in the proof, and each line in the proof where that piece of information is used.

Proof:

Two triangles have 2 pairs of corresponding sides congruent, and the corresponding angles between those sides are congruent.

Use one of those proofs to guide you in writing a proof for this situation.

It follows from the Side-Angle-Side Triangle Congruence Theorem that if the lengths of 2 sides of a triangle are known, and the measure of the angle between those 2 sides is known, there can only be one possible length for the third side.

Mai and Kiran want to prove that in an isosceles triangle, the 2 base angles are congruent. Finish the proof that they started.

2.

Geo.2.6 Practice

2.1.

IM Geo.2.6 Practice: Side-Angle-Side Triangle Congruence

Triangle DAC is isosceles with congruent sides AD and AC.

Tyler has written an incorrect proof to show that quadrilateral ABCD is a parallelogram.

Triangles ACD and BCD are isosceles.

Here are some statements about 2 zigzags. Put them in order to prove figure ABC is congruent to figure DEF.

Match each statement using only the information shown in the pairs of congruent triangles.

Triangle ABC is congruent to triangle EDF.

Information