[size=150]Die Grundgleichung für lineare Funktionen lautet[/size]:[br][br][color=#9900ff][size=100] [size=150] [table][tr][td][color=#9900ff][size=100][size=150][size=200]y=mx+b[/size][/size][/size][/color][/td][td] [color=#0000ff] m- Steigung[br] b- Y-Achsenabschnitt[/color][/td][/tr][/table][/size][size=150][table][tr][td][br][/td][/tr][/table][/size][/size][/color]
Die [color=#0000ff][i]Steigung[/i][/color] [i][color=#0000ff]m [/color][/i]gibt an, um wie viele y-Einheiten ([math]\bigtriangleup y[/math]) sich der Graph der Funktion im Verhältnis zur Änderung der x-Einheiten ([math]\bigtriangleup x[/math]) ändert. [br][math]\Longrightarrow[/math]Wie steil oder flach der Graph der Funktion steigt/fällt. [br][br]Allgemeine Formel:[br][br]m=[math]\frac{\bigtriangleup y}{\bigtriangleup x}=\frac{y_2-y_1}{x_2-x_1}[/math]
Das [color=#0000ff][i]Steigungsdreieck[/i][/color] ist die grafisch Darstellung der Steigung der Funktion.[br]Auch an dem obrigen Graph einer Funktion ist ein blaues Steigungsdreieck.
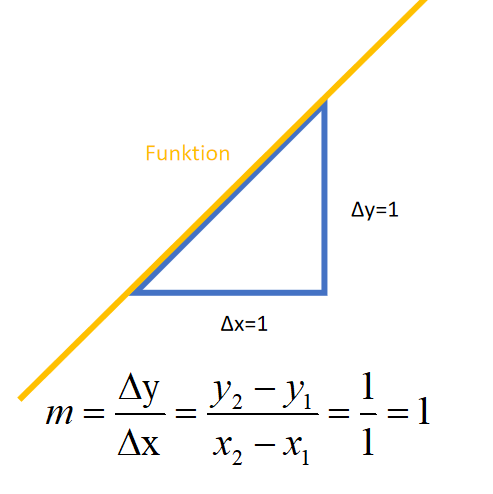
[size=100][i]Abb.1.1[br][/i]In der Abbildung ist eine Funktion erkennbar, an der ein[color=#0000ff][i] Steigungsdreieck[/i][/color] anliegt.[br]Du siehst, dass sich der Graph der Funktion um eine x-Einheit ([math]\bigtriangleup x[/math])[br]nach rechts und um eine y-Einheit ([math]\bigtriangleup y[/math]) nach oben bewegt.[br]Wenn du die Werte in die Formel m=[math]\frac{\bigtriangleup y}{\bigtriangleup x}[/math] einsetzt, so erhälst du eine Steigung von m=1.[/size]
Der [color=#ff0000][i]y-Achsenabschnitt b[/i][/color] gibt an, an welcher Stelle der y-Achse der Graph der Funktion diese schneidet.
