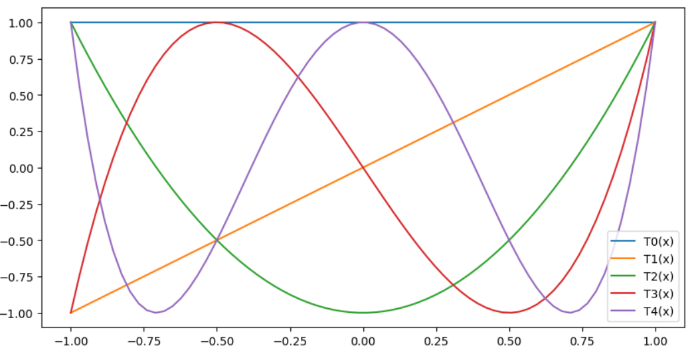
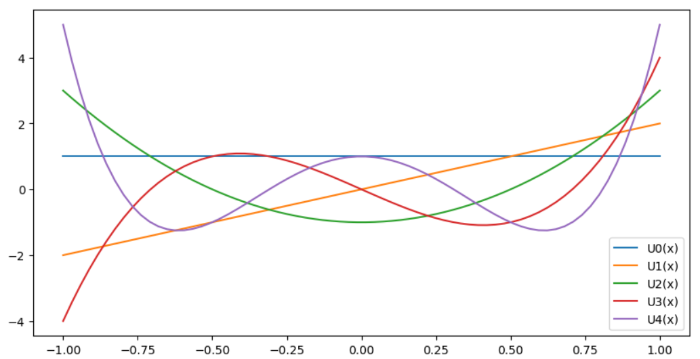
[size=150][b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][br][/b]前回まで、微分方程式の解法を通して、ルジャンドルとか、ベッセルとか、[br]特殊な関数、多項式に触れてきた。[br]今回は、他にもある特殊な関数、多項式をみてみよう。[br][b][br][size=150][b]＜チェビシェフの微分方程式＞[/b][/size][br][/b][/size]p(x)=1-x[sup]2[/sup],q(x)=-x , r(x)=n[sup]2[/sup] はｘ＝０で解析的で、(1−x[sup]2[/sup])y′′−xy′+n[sup]2[/sup]y=0を[br]チェビシェフの微分方程式という。x=0は正則点。[br]・級数解y=Σa[sub]m[/sub]x[sup]m[/sup]=a[sub]0[/sub]+a[sub]1[/sub]x+a[sub]2[/sub]x[sup]2[/sup]+a[sub]3[/sub]x[sup]3[/sup]....（a[sub]0[/sub]≠0, m for 0 to ∞)を入れてみよう。[br]y'=a[sub]1[/sub]+2a[sub]2[/sub]x[sup]1[/sup]+3a[sub]3[/sub]x[sup]2[/sup]+......[br]y"=2*1a[sub]2[/sub]+3*2 a[sub]3[/sub]x + ...[br]p(x)=1-x[sup]2[/sup][br]q(x)=-x[br]r(x)=＋n[sup]2[/sup][br]2*1a[sub]2[/sub]+3*2 a[sub]3[/sub]x + ...+(k+2)(k+1) a[sub]k+2[/sub]x[sup]k[/sup] +..... [br]-(2*1a[sub]2[/sub]x[sup]2[/sup]+3*2a[sub]3[/sub]x[sup]3[/sup] ...+k*(k-1) a[sub]k[/sub]x[sup]k[/sup] .......)[br]-(a[sub]1[/sub]x+2a[sub]2[/sub]x[sup]2[/sup]+3a[sub]3[/sub]x[sup]3[/sup]+......ka[sub]k[/sub]x[sup]k[/sup]+.......)[br]+n[sup]2[/sup](a[sub]0[/sub]+a[sub]1[/sub]x+a[sub]2[/sub]x[sup]2[/sup]+a[sub]3[/sub]x[sup]3[/sup]....+a[sub]k[/sub]x[sup]k[/sup]......)=0[br]x[sup]0[/sup]係数の和は、2a[sub]2[/sub]+n[sup]2[/sup]a[sub]0[/sub]=0 a[sub]2[/sub]=(0-n[sup]2[/sup])/2*1 a[sub]0[/sub][br]x[sup]1[/sup]係数の和は、3*2 a[sub]3 [/sub]-1a[sub]1 [/sub]+n[sup]2[/sup]a[sub]1[/sub]=0 a[sub]3 [/sub]=(1-n[sup]2[/sup])/3*2 a[sub]1[br][/sub]x[sup]2[/sup]の係数の和は、4*3 a[sub]4[/sub] -2a[sub]2[/sub]-2*1a[sub]2[/sub] +n[sup]2[/sup]a[sub]2 [/sub]=0 a[sub]4 [/sub]=(2[sup]2[/sup]-n[sup]2[/sup])/4*3 a[sub]2[br][/sub]x[sup]3[/sup]の係数の和は、5*4a[sub]5[/sub] -3a[sub]3[/sub]-3*2a[sub]3[/sub] +n[sup]2[/sup]a[sub]3 [/sub]=0 5*4 a[sub]5[/sub] -(3+3*2-n[sup]2[/sup])a[sub]3 [/sub]=0 a[sub]5 [/sub]=(3[sup]2[/sup]-n[sup]2[/sup])/5*4 a[sub]1[br][/sub]x[sup]k[/sup]の係数の和は、(k+2)(k+1) a[sub]k+2[/sub] -ka[sub]k[/sub]-k(k-1)a[sub]k[/sub] +n[sup]2[/sup]a[sub]k [/sub]= (k+2)(k+1)a[sub]k+2[/sub] -(k+k[sup]2[/sup]-k-n[sup]2[/sup])a[sub]k [/sub]=0[br]　[math]a_{k+2}=\frac{(k^2-n^2)}{(k+2)(k+1)}a_k[/math][br]これから、a0から始めると、[br]・a_even= [math]a_{2m}=\frac{(\left(2m-2\right)^2-n^2)....\left(-n^2\right)}{(2m)(2m-1)....2\cdot1}a_0=\frac{\left(-n^2\right)....\left(\left(2m-2\right)^2-n^2\right)}{\left(2m\right)!}a_0[/math][br]a1から始めると、[br]・a_odd = [math]a_{2m+1}=\frac{(\left(2m-1\right)^2-n^2)....\left(1-n^2\right)}{(2m+1)(2m)....2}a_1=\frac{\left(1-n^2\right)....\left(\left(2m-1\right)^2-n^2\right)}{\left(2m+1\right)!}a_1[/math] [br]これこら、一般解はｙ＝a0y0(x)+a1y1(x)で、[br]y0(x)=1+(-n[sup]2[/sup])/2! x[sup]2[/sup]+(-n[sup]2[/sup])(2[sup]2[/sup]-n[sup]2[/sup])/4! x[sup]4[/sup]+(-n[sup]2[/sup])(2[sup]2[/sup]-n[sup]2[/sup])(4[sup]2[/sup]-n[sup]2[/sup])/6! x[sup]6[/sup]+...........[br]y1(x)=x+(1-n[sup]2[/sup])/3! x[sup]3[/sup]+(1-n[sup]2[/sup])(3[sup]2[/sup]-n[sup]2[/sup])/5! x[sup]5[/sup]+(1-n[sup]2[/sup])(3[sup]2[/sup]-n[sup]2[/sup])(5[sup]2[/sup]-n[sup]2[/sup])/7! x[sup]7[/sup]+...........[br][br][b][size=150]＜チェビシェフの多項式＞[br][/size][/b]・(1−x[sup]2[/sup])y′′−xy′+n[sup]2[/sup]y=0 の第一のチェビシェフの多項式Tn(x)は、nの偶奇で式を変える。[br]n=2s（偶数）のとき、Tn(x)=(-1)[sup]s[/sup]y0(x)、奇数n=2s+1のとき、T[sub]n[/sub](x)= (-1)[sup]s [/sup]n y1(x)。[br]漸化式の[math]a_{k+2}=\frac{(k^2-n^2)}{(k+2)(k+1)}a_k[/math] のn＝ｋになったとき、k+2番目以降は０になる。[br]だから、[b][color=#0000ff]Tn(x)はn次式になる[/color][/b]。[br]T0(x)= 1,[br]T1(x)= x, [br]T2(x)= -(1-2x[sup]2[/sup])= 2x[sup]2[/sup]-1,[br]T3(x)= -3(x+(1-9)/6x[sup]3[/sup])= 4x[sup]3 [/sup]-3x[br]T4(x)= (-1)[sup]2[/sup](1-4[sup]2[/sup]/2! x[sup]2[/sup]+(-4[sup]2[/sup])(2[sup]2[/sup]-4[sup]2[/sup])/4! x[sup]4[/sup])=1-8x[sup]2[/sup]+8x[sup]4 [/sup]=8x[sup]4 [/sup]-8x[sup]2 [/sup]+1[br]............[br]チェビシェフの多項式が面白いのは、[b][color=#0000ff]ｘ=cos θを代入すると、cos n θを表すｎ倍角の公式になることだ[/color][/b]。[br]T0(cos θ)= 1 = cos0θ,[br]T1(cos θ)= cos θ = cos 1θ, [br]T2(cos θ)= 2(cos θ)[sup]2[/sup]-1=cos 2θ[br]T3(cos θ)= 4(cos θ)[sup]3 [/sup]-3(cos θ)=cos 3θ[br]T4(cos θ)=8(cos θ)[sup]4 [/sup]-8(cos θ)[sup]2 [/sup]+1 = cos 4θ [br].............[br][b][color=#0000ff]Tn(cos θ)= cos nθ[/color][/b][br]cos θ=x ( θ= arccos x）を代入するともとに戻るので、[b]Tn(x)=cos(n θ) = cos(n arccos x)[/b] [br][br][b][size=150]＜フロベニウス法＞[br][/size][/b]一般解を級数解y=Σa[sub]m[/sub]x[sup]m+r[/sup]=x[sup]r[/sup](a[sub]0[/sub]+a[sub]1[/sub]x+a[sub]2[/sub]x[sup]2[/sup]+a[sub]3[/sub]x[sup]3[/sup]....)（a[sub]0[/sub]≠0, m for 0 to ∞)を入れてみよう。[br]として、 x[sup]r−2[/sup] の係数 r(r−1)a0=0から、決定方程式の[b]解がr=0,1[/b]となります。[br]だから、r=0としたものが上記の解と多項式だとわかります。[br][br]もしr=1にすると、上と同様な計算によって、漸化式ak+2​=[(k+1)[sup]2[/sup]−n[sup]2[/sup]]/​(k+3)(k+2)ak​​ [br]が得られてこれを累積して係数を作ればy0(x),y1(x)ができるね。[br]nに偶数、奇数で分けて同様のロジックで計算していくと[br]第2種チェビシェフの多項式Un(x)ができるのです。[br][br]U0(x)= 1,[br]U1(x)= 2x, [br]U2(x)= 4x[sup]2[/sup]-1,[br]U3(x)= 8x[sup]3 [/sup]-4x[br]....................第２チェビシェフの多項式にも、[b][color=#0000ff]ｘ=cos θを代入してみよう。[/color][/b][br]U0(cos θ)= 1 ,[br]U1(cos θ)= 2cos θ , [br]U2(cos θ)= 4(cos θ)[sup]2[/sup]-1[br]U3(cos θ)= 8(cos θ)[sup]3 [/sup]-4(cos θ)[br]かんたんな式ではありませんが、[b][color=#0000ff]Un(cosθ)=sin((n+1)θ)/ sinθ[/color][/b]になります。[br]だから、cos θ=x ( θ= arccos x）を代入すると[b]Un(x)=sin((n+1) arccos x)/√(1- x[sup]2[/sup])[/b]

[b][size=150]＜ド・モアブル定理から＞[/size][/b][br]チェビシェフ多項式は、別の入り口からも手に入る。[br]まず、[color=#0000ff]ド・モアブル定理[/color]（cosθ+i sinθ) [sup]n[/sup]=cos n θ＋i sin n θ[br] これは、文字列として見るのではなく、[color=#0000ff]オイラー等式[/color]からcosθ+i sinθ=e[sup]iθ[br][/sup] と考えれば、θの回転をｎ回やれば、到達する複素数はｎ倍のθの複素数になるので、当然だね。[br]また、[color=#0000ff]2項定理[/color]（a + b)[sup]n[/sup]=Σ [sub]n[/sub]C[sub]k[/sub] a[sup]k[/sup]b[sup]n-k[/sup][sub] [/sub][k for 0 to n][sub][br][/sub]から、（cosθ+i sinθ) [sup]n[/sup]=Σ [sub]n[/sub]C[sub]k[/sub] cosθ[sup]k[/sup](i sinθ)[sup]n-k[br][/sup]= cos[sup]n[/sup]θ+ i cos [sup]n-1[/sup]θsin[sup]1[/sup]θ - cos [sup]n-2[/sup]θsin[sup]2[/sup]θ - i cos [sup]n-3[/sup]θsin[sup]3[/sup]θ + cos [sup]n-4[/sup]θsin[sup]4[/sup]θ + i - -i + .......[br]=( cos[sup]n[/sup]θ- cos [sup]n-2[/sup]θsin[sup]2[/sup]θ + cos [sup]n-4[/sup]θsin[sup]4[/sup]θ - cos [sup]n-6[/sup]θsin[sup]6[/sup]θ +- .........)[br]+i(cos [sup]n-1[/sup]θsin[sup]1[/sup]θ - cos [sup]n-3[/sup]θsin[sup]3[/sup]θ + cos [sup]n-5[/sup]θsin[sup]5[/sup]θ - cos [sup]n-7[/sup]θsin[sup]7[/sup]θ +-...........)[br]以上から、[br] cos nθ= cos[sup]n[/sup]θ- cos [sup]n-2[/sup]θsin[sup]2[/sup]θ + cos [sup]n-4[/sup]θsin[sup]4[/sup]θ - cos [sup]n-6[/sup]θsin[sup]6[/sup]θ +- .........[br] sin nθ= cos [sup]n-1[/sup]θsin[sup]1[/sup]θ - cos [sup]n-3[/sup]θsin[sup]3[/sup]θ + cos [sup]n-5[/sup]θsin[sup]5[/sup]θ - cos [sup]n-7[/sup]θsin[sup]7[/sup]θ +-...........だから、[br] sin (n+1)θ= cos [sup]n[/sup]θsin[sup]1[/sup]θ - cos [sup]n-2[/sup]θsin[sup]3[/sup]θ + cos [sup]n-4[/sup]θsin[sup]5[/sup]θ - cos [sup]n-6[/sup]θsin[sup]7[/sup]θ +-...........[br]となるね。[br]ここで、cos θ＝ｘとして、[br]（cosθ+i sinθ) [sup]n[/sup]=cos n θ＋i sin n θの実部cosnθ=ｘの式＝Tn(x)とし、[br]（cosθ+i sinθ) [sup]n+1[/sup]=cos (n+1)θ＋i sin (n+1)θの虚部sin(n+1)θ=sinθ(xの式）のｘの式をUn(x)とする。[br]こういうTn(x),Un(x)を第１、第２のチェビシェフの多項式と決めることができる。[br]

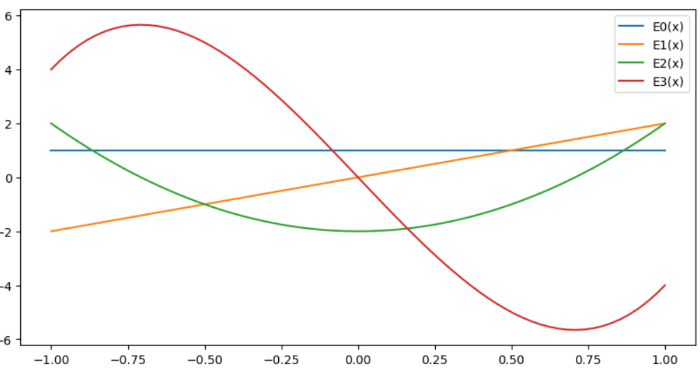
[b][size=150]＜微分方程式＞[/size][/b][br]p(x)=-2x,q(x)=2α はｘ＝０で解析的で、y′′−2xy′+2ky=0を[br]エルミートの微分方程式という。x=0は正則点。[br]・級数解y=Σa[sub]m[/sub]x[sup]m[/sup]=a[sub]0[/sub]+a[sub]1[/sub]x+a[sub]2[/sub]x[sup]2[/sup]+a[sub]3[/sub]x[sup]3[/sup]....（a[sub]0[/sub]≠0, m for 0 to ∞)を入れてみよう。[br]y'=a[sub]1[/sub]+2a[sub]2[/sub]x[sup]1[/sup]+3a[sub]3[/sub]x[sup]2[/sup]+......[br]y"=2*1a[sub]2[/sub]+3*2 a[sub]3[/sub]x + ...[br]p(x)=-2x[br]q(x)=2α[br]2*1a[sub]2[/sub]+3*2 a[sub]3[/sub]x + ...+(k+2)(k+1) a[sub]k+2[/sub]x[sup]k[/sup] +..... [br]-(2a[sub]1[/sub]x+4a[sub]2[/sub]x[sup]2[/sup]+6a[sub]3[/sub]x[sup]3[/sup]+......2k a[sub]k[/sub]x[sup]k[/sup]+.......)[br]+2α(a[sub]0[/sub]+a[sub]1[/sub]x+a[sub]2[/sub]x[sup]2[/sup]+a[sub]3[/sub]x[sup]3[/sup]....+a[sub]k[/sub]x[sup]k[/sup]......)=0[br]x[sup]0[/sup]係数の和は、2a[sub]2[/sub]+2αa[sub]0[/sub]=0 a[sub]2[/sub]=2(0-α)/2*1a[sub]0[/sub][br]x[sup]1[/sup]係数の和は、3*2 a[sub]3 [/sub]-2a[sub]1 [/sub]+2αa[sub]1[/sub]=0 a[sub]3 [/sub]=2(1-α)/ 3*2a[sub]1[br][/sub]x[sup]2[/sup]の係数の和は、4*3 a[sub]4[/sub] -4a[sub]2 [/sub]+2αa[sub]2 [/sub]=0 a[sub]4 [/sub]=2(2-α)/ 4*3a[sub]2[br][/sub]x[sup]3[/sup]の係数の和は、5*4a[sub]5[/sub] -6a[sub]3[/sub]+2αa[sub]3 [/sub]=0 a[sub]5[/sub] =2(3 -α[sup][/sup])/5*4 a[sub]3 [/sub][sub][br][/sub]x[sup]k[/sup]の係数の和は、(k+2)(k+1) a[sub]k+2[/sub] -2ka[sub]k [/sub]+2α a[sub]k [/sub]= (k+2)(k+1)a[sub]k+2[/sub] -2(k -α)a[sub]k [/sub]=0[br] [math]a_{k+2}=\frac{2(k-\alpha)}{(k+2)(k+1)}a_k[/math]　[br]a_even= [math]a_{2s}=\frac{2^s\left(2s-2-\alpha\right)\left(2s-4-\alpha\right)....\left(0-\alpha\right)}{\left(2s\right)!}a_0[/math] , [br] a_odd= [math]a_{2s+1}=\frac{2^s(2s-1-\alpha)\left(2s-3-\alpha\right)....\left(1-\alpha\right)}{\left(2s+1\right)!}a_1[/math] [br]y=a0y0(x) + a1y1(x)が一般解。 [br]y0(0)=Σ [math]\frac{2^s(2s-2-\alpha)\left(2s-4-\alpha\right)....\left(0-\alpha\right)}{\left(2s\right)!}x^{2s}[/math] [sup] [/sup][s for 0 to ∞][br]y1(0)=Σ [math]\frac{2^s(2s-1-\alpha)\left(2s-3-\alpha\right)....\left(1-\alpha\right)}{\left(2s+1\right)!}x^{2s+1}[/math] [sup] [/sup][s for 0 to ∞][br]・αが偶数2nのときは、a0=1, a1=0とすると、y=y0(x)となるね。[br]　漸化式 [math]a_{k+2}=\frac{2(k-\alpha)}{(k+2)(k+1)}a_k[/math] の分子の因数k-αのために、[br] k=α次の係数のあとはすべて０になるから、2n次の多項式になる。[br]・αが奇数2n+1のときも同様にして、y=y1(x)となり、2n+1次の多項式になる。[br]　これらがエルミート多項式だ。[br][b][size=150]＜多項式＞[br][/size]最高次ｘ[sup]k[/sup]の係数が2[sup]k[/sup]になるとしたら、[br][/b]・最高次数k=α=2nのときに、その係数が2[sup]2n[/sup]になる。[br]　漸化式の最後の分子は(2n-2- 2n),分母は2n*(2n-1)となるから、[br] [math]\frac{2^n(2n-2-2n)\left(2n-4-2n\right)....\left(0-2n\right)}{\left(2n\right)!}a_0=2^{2n}[/math] [sup] [br] [math]a_0=2^{2n}\frac{\left(2n\right)!}{2^n(2n-2-2n)\left(2n-4-2n\right)....\left(0-2n\right)}=2^n\frac{\left(2n\right)!}{(-2)\left(-4\right)....\left(0-2n\right)}=\left(-2\right)^n\left(2n-1\right)!![/math] [sup] [br][/sup][/sup]ここで、2重階乗マーク!!は、１飛ばしで連続奇数の積を表すね。[br]・最高次数k=α=2n＋1のときも同様にして、a1=(-1)[sup]n[/sup]2[sup]n+1[/sup](2n+1)!![br]　とする。[br]このとき、Hn(x)=a0 y0(x)+a1y1(x)をエルミート多項式という。[br]　a0=(-1)[sup]n[/sup](2n-1)!!, a1=(-1)[sup]n[/sup]2[sup]n+1[/sup](2n+1)!![br]H0(x)=a0=(-2)[sup]0[/sup](2*0-1)!!=1[br]H1(x)=a1x=(-1)[sup]0[/sup]2[sup]0+1[/sup](2*0+1)!!x=2x[br]H2(x)=(-2)[sup]1[/sup](2*1-1)!!(1+2*(-2)/2!x[sup]2[/sup])=4x[sup]2[/sup]-2[br]H3(x)=(-1)[sup]1[/sup]2[sup]1+1[/sup](2*1+1)!!(1x+2(1-3)/ 3*2 x[sup]3[/sup]) =-12(1x -2/3x[sup]3[/sup])=8x[sup]3[/sup] -12x[br]...................[br]エルミート多項式にも、微分形式のものがありますね。[br][b]Hn(x)=(-1)[sup]n[/sup]exp(x[sup]2[/sup]) (exp(-x[sup]2[/sup]))[sup](n)[/sup][/b]

[color=#9900ff][u][b][size=150]質問：チェビシェフの多項式やエルミート多項式をグラフ表示するコードはどうすれば作れますか。[br][/size][/b][/u][/color][br]特殊関数ということで、ベッセル関数と同様にscipy.specialからインポートできますね。[br]チェビシェフ第１多項式はTn(x)=[b]eval_chebyt(n,x)[/b]でえられます。[br]チェビシェフ第２多項式はUn(x)=[b]eval_chebyu(n,x)[/b]でえられます。[br]エルミート多項式はEn(x)=[b]eval_hermite(n,x)[/b]でえられます。[br]x = np.linspace(-1, 1, 70)とすることで、ｘが-1から1の間で計算しました。[br]# チェビシェフ多項式[br][color=#0000ff]import numpy as np[br]import matplotlib.pyplot as plt[br]from scipy.special import [b]eval_chebyt[/b][br]fig = plt.figure(figsize=(10,5))[br]ax = fig.add_subplot(111)[br]x = np.linspace(-1, 1, 70)[br]for n in range(5):[br] ax.plot(x, eval_chebyt(n, x), label=f"T{n}(x)")[br]ax.legend()[/color]

# チェビシェフ多項式第２[br]import numpy as np[br]import matplotlib.pyplot as plt[br]from scipy.special import [b]eval_chebyu[/b][br]fig = plt.figure(figsize=(10,5))[br]ax = fig.add_subplot(111)[br]x = np.linspace(-1, 1, 70)[br]for n in range(5):[br] ax.plot(x, [b]eval_chebyu[/b](n, x), label=f"U{n}(x)")[br]ax.legend()

# エルミート多項式[br]import numpy as np[br]import matplotlib.pyplot as plt[br]from scipy.special import eval_hermite[br]fig = plt.figure(figsize=(10,5))[br]ax = fig.add_subplot(111)[br]x = np.linspace(-1, 1, 70)[br]for n in range([b]4[/b]):[br] ax.plot(x, eval_hermite(n, x), label=f"E{n}(x)")[br]ax.legend()