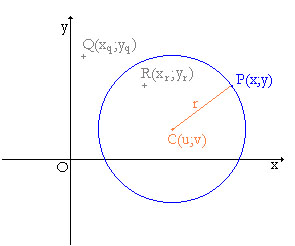
A kör egyenlete
A körvonal azoknak a pontoknak a halmaza ([url=http://www.bethlen.hu/matek/mathist/forras/Mertani_helyek.htm][u]mértani helye[/u][/url]) a síkban, amelyek a sík egy adott pontjától, (a kör középpontjától) adott távolságban vannak.[br]Ez a távolság a kör sugara. [br][br][table][tr][td]Adott a [url=http://www.bethlen.hu/matek/mathist/forras/Koordinata_rendszer.htm][u]koordináta rendszerben [/u][/url]a C(u;v) középpontú, és r sugarú kör.(Lásd a mellékelt animációt.) A körvonal bármely P(x;y) pontja C(u;v) középponttól adott r távolságra van A C és P pontok távolságára felírva a [url=http://www.bethlen.hu/matek/mathist/forras/Ket_pont_tavolsaga.htm][u]két pont távolságára[/u][/url] vonatkozó összefüggést:[br]Ezt négyzetre emelve:[b][i][color=#0000ff](x-u)[sup]2[/sup]+(y-v)[sup]2[/sup]=r[sup]2[/sup][/color][/i][/b][br][/td][/tr][/table]
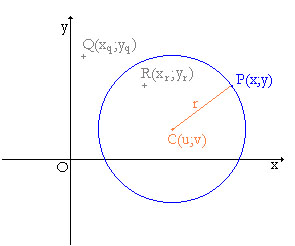
Ezt az [url=http://www.bethlen.hu/matek/mathist/forras/Alakzat_egyenlete.htm][u]egyenletet[/u][/url] a C(u;v) középpontú, r sugarú körvonal minden pontjának koordinátái kielégítik, és más pont koordinátái pedig nem.Ez az egyenlet a kör egyenlete.Egy körön kívüli Q(x[sub]q[/sub];y[sub]q[/sub]) pont esetén[color=#0000ff] [/color][b][i][color=#0000ff](x[sub]q[/sub]-u)[sup]2[/sup]+(y[sub]q[/sub]-v)[sup]2[/sup]>r[/color][sup][color=#0000ff]2[/color][br][/sup][/i][/b]Egy körön belüli R(x[sub]q[/sub];y[sub]q[/sub]) pont esetén [b][i][color=#0000ff](x[sub]q[/sub]-u)[sup]2[/sup]+(y[sub]q[/sub]-v)[sup]2[/sup]<r[sup]2[br][/sup][/color][/i][/b]Abban a speciális esetben, amikor a kör középpontja az origó, tehát C(0;0), akkor az egyenlet a következő alakban írható:[color=#0000ff] [/color][b][i][color=#0000ff]x[sup]2[/sup]+y[sup]2[/sup]=r[/color][sup][color=#0000ff]2[/color][br][/sup][/i][/b]