[b]=> [color=#0000ff]Punkt [/color]wandert auf einer [color=#38761d]Funktion[/color] (z.B. Gerade)[/b]
Funktionale Abhängigkeiten
Table of Contents
- Streckenlängen im Koordinatensystem
- Grundseite eines Dreiecks bestimmen im KOSY
- Dreieck mit Variable
- Vorüberlegung zur funktionalen Abhängigkeit
- Begriffe "funktionale Abängigkeit"
- Begriffe
- Funktionale Abhängigkeit
- Musteraufgabe - Funktionale Abhängigkeiten
- Höhe horizontal
- Drachenviereck in Abhängigkeit von x
- Determinante
- Wiederholung Determinante
- Leichte Aufgabe zu funktionaler Abhängigkeit mit Determinante
- Flächeninhalt Parallelogramm
- Verlängern und Verkürzen
- Funktionale Abhängigkeiten ohne Koordinatensystem
Grundseite eines Dreiecks bestimmen im KOSY
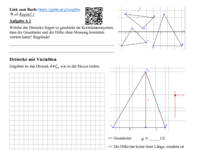
Aufgabe A1
Welche der Dreiecke liegen so geschickt im Koordinatensystem,[br]dass die Grundseite und die Höhe ohne Messung bestimmt werden kann? Begründe![br][br][br]
Welches Dreieck?
Begründung:
Verändere das Dreieck ABC am Punkt B so, dass du die Grundseite und die Höhe ablesen kannst.
Vorüberlegung zur funktionalen Abhängigkeit
Dreieck mit Variable
Gegeben ist das Dreieck ABC[sub]n[/sub] wie in der Skizze.[br][br]
Länge der Grundseite in LE:
Die Höhe hat keine feste Länge, sondern ist variabel.[br]Betrag der Höhe in LE:
Aufgabe A2
A 2.1 Für welche Werte von x lässt sich kein Dreieck zeichnen?[br]A 2.2 Zeichne das Dreieck ABC[sub]1[/sub] für x=6.[br]A 2.3 Berechne den Flächeninhalt A(x) für x=6.[br]A 2.4 Bestimme den Flächeninhalt in Abhängigkeit von x.[br]A 2.5 Für welchen Wert von x entsteht ein rechtwinkliges Dreieck? (=> Tipp: Zeichnung!)
Begriffe
funktional
[b]=> dieser [color=#0000ff]Punkt[/color] ist Teil einer Figur[/b]
Abhängigkeit
[b]=> Die Lage des Punktes ändert den Flächeninhalt der Figur (oder die Länge der Strecke)[br][br]=> Der Flächeninhalt des Dreiecks ist abhängig von der Lage des Punktes.[br][br][br][/b]
Musteraufgabe - Funktionale Abhängigkeiten
Musteraufgabe
[b]Gegeben[/b][b] ist die Geraden g mit der [b]Gleichung [/b]g: y = 0,5x + 3 .[/b][br][b]Der Punkt C[sub]n[/sub] wandert auf der Geraden g und besitzt die Koordinaten [/b][b]C[sub]n[/sub][/b][b](x|0,5x+3).[/b][br][b]Mit den festen Punkte A (-2|-1) und B (4|-1) und dem Punkt C[sub]n[/sub](x|0,5x+3) entstehen Dreiecke ABC[sub]n[/sub].[/b][br][br][b]a) Zeichne die Punkte A, B und die Gerade g in das Koordinatensystem ein.[/b][br][b]b) Zeichne das Dreieck ABC[sub]1[/sub] für x = 2 und das Dreieck ABC[sub]2 [/sub]für x = 7.[/b][br][b]c) Berechne den Flächeninhalt A[sub]1[/sub] und A[sub]2[/sub] der beiden Dreiecke. [/b][br][b]d) Für welche Werte von x entstehen Dreiecke ABC[sub]n[/sub]?[/b][br][b]e) Bestimme den Flächeninhalt A(x) der Dreiecke ABC[sub]n[/sub] in Abhängigkeit der Abszisse x der Punkte C[sub]n[/sub].[/b][br][b]f) Behauptung: [i]„Unter den Dreiecken ABC[/i][sub][i]n [/i][/sub][i]gibt es drei rechtwinklige.“[/i][/b][br]
[b]Bestimme[/b][b] den Flächeninhalt A(x) der Dreiecke ABC[sub]n[/sub] in Abhängigkeit[/b][b] der Abszisse x der Punkte C[sub]n[/sub].[/b][br]
Lernvideo zur Musteraufgabe
Lösung der Übungsaufgabe Arbeitsblatt
Wiederholung Determinante
Link zum Buch aus Jahrgangsstufe 7 "Parallelverschiebung"
https://www.geogebra.org/m/f9ua6ejw#material/czdvxmnu
Funktionale Abhängigkeiten ohne Koordinatensystem
Aufgabe ähnlich AP 2016 A2
Die Zeichnung zeigt das Trapez ABCD mit [math]\left[AB\right]\parallel\left[CD\right][/math] .[br]Es gilt: [math]\overline{AB}=9cm[/math]; [math]\overline{CD}=4,5cm[/math]; [math]\overline{AL}=3cm[/math]; [math]\overline{DL}=4cm[/math] .[br][br][b]Verlängert [/b]man die Seite [AB] über B hinaus um x cm und [br][b]verkürzt [/b]gleichzeitig die Strecke [DL] von D aus um x cm, [br]so entstehen für [math]x\in\mathbb{R};x\in\sqsupset0;4\sqsubset[/math] Trapeze AB[sub]n[/sub]C[sub]n[/sub]D[sub]n[/sub] mit [AB[sub]n[/sub]] || [C[sub]n[/sub]D[sub]n[/sub]] und [math]\overline{C_nD_n}=4,5cm[/math] .[br][br]Du kannst dir das Trapez AB[sub]n[/sub]C[sub]n[/sub]D[sub]n[/sub] anzeigen lassen und mit dem Schieberegler den Wert für x verändern.
A1
Für welchen Wert für x entsteht ein gleichschenkliges Trapez?
A2
Welcher Term beschreibt den Flächeninhalt der Trapeze AB[sub]n[/sub]C[sub]n[/sub]D[sub]n[/sub] in Abhängigkeit von x?[br]Rechne zuerst und entscheide dann.
A3
Kennst du den Satz des Pythagoras schon?[br]Wie lang ist die Strecke [AD]? Berechne im Kopf!