Honors Algebra 2
This book contains sketches created for my Honors Algebra 2 class at Stuyvesant High School
Tabla de Contenidos
- Trigonometry
- Unit Circle Trigonometry
- Unit Circle: Complementary Angles
- Unit Circle: Sine and Cosine Functions
- Graph of Cosine
- Graphing Sine/Cosine with Translations
- Graphing the Tangent Function
- Lighthouse Function p.553 #69
- Cosine of the Difference of Two Angles
- The Ambiguous Case of SSA
- Complex Numbers
- Multiplying Complex Numbers
- Exponential and Logarithmic Functions
- Exponential graph as 2-variable function
- Conic Sections
- Drawing a Parabola
- Locus Definition of a Parabola
- Parabola Properties
- Parabola: Reflective Property and Distance
- Systems of Equations
- Intersection of a Parabola and a Line
- Intersection of Two Circles
- Intersection of a Circle and Parabola
- Intersection of Two Parabolas
- Intersections of Planes
- Statistics and Probability
- Normal Distribution - Data Collection
- Normal Distribution
- Sample Means
- Distribution of Sample Means
- Sample Means 1
- Sample Means 2
- Tossing a fair coin n times
- Comparing Normal and Binomial Distributions
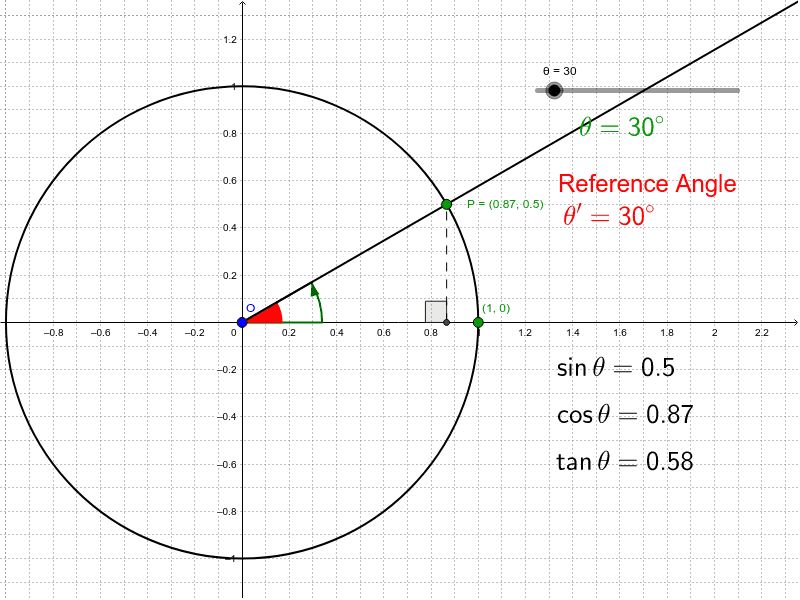
Unit Circle Trigonometry
Drag the slider for [math]\theta[/math] to adjust the angle. Notice the coordinates of point [math]P[/math] on the unit circle.
Unit Circle Definition of Trig Functions
We can extend the definitions of sine, cosine and tangent (and their reciprocals) to angles of [i]any[/i] measure, by using the unit circle.[br][br]On the unit circle, if the point [math]P[/math] has coordinates [math]\left(x,y\right)[/math], then from the right triangle we can see that, in Quadrant I:[br][math]x=\cos\theta[/math][br][math]y=\sin\theta[/math][br][math]\frac{y}{x}=\tan\theta[/math][br][br]Therefore, the point where the terminal side of [math]\theta[/math] intersects the the unit circle will have coordinates [math]P\left(\cos\theta,\sin\theta\right)[/math], assuming the angle is in standard position.[br][br]Since the signs of the coordinates depend on the quadrant, the signs of sine, cosine, and tangent will also depend on the quadrant.[br][br]We can determine the coordinates of the point on the unit circle by using [math]\theta'[/math], the [i]reference angle[/i] of [math]\theta[/math]. This is the acute angle formed between the terminal side of [math]\theta[/math] and the [math]x[/math]-axis. Completing the right triangle will get us the ratios for [math]\theta'[/math], which will be identical to the ratios for [math]\theta[/math], except that we may need to attach a negative sign depending on the quadrant.[br][br]You can drag the slider for the angle and see how the red reference angle changes and where the right triangle is that will allow us to find the coordinates of the point on the unit circle and, in turn, the ratios of [math]\theta[/math].
Multiplying Complex Numbers
This graph shows how we can interpret the multiplication of complex numbers geometrically.[br]Given two complex numbers:[br][math]w=a+bi[/math], [math]z=c+di[/math] where [math]a,b,c,d\in\mathbb{R}[/math][br][br]Consider their product[br][math]wz=\left(a+bi\right)z=az+biz[/math][br][table][tr][td]1[/td][td][math]az[/math]ļ»æ[/td][td]Dilate [math]z[/math]ļ»æ by a scale factor of [math]a[/math][/td][/tr][tr][td]2[/td][td][math]iz[/math]ļ»æ[/td][td]ļ»æRotate [math]z[/math] by [math]90^\circ[/math] about [math]0[/math][/td][/tr][tr][td]3ļ»æ[/td][td]ļ»æ[math]biz[/math][/td][td]ļ»æDilate [math]iz[/math] by a scale factor of [math]b[/math][/td][/tr][tr][td]ļ»æ4[/td][td]ļ»æ[math]az+biz[/math][/td][td]ļ»æTranslate [math]az[/math] by [math]biz[/math][/td][/tr][/table][br]Focus on the two right triangles in the diagram:[br][list=1][*]The right triangle formed by [math]w[/math], [math]0[/math] and the positive real axis.[/*][*]The right triangle formed by [math]az[/math], [math]biz[/math] and [math]0[/math][br][br][/*][/list]The first right triangle has sides of length: [math]a[/math], [math]b[/math], [math]\left|w\right|[/math].[br]The second right triangle has sides of length [math]a\left|z\right|[/math], [math]b\left|z\right|[/math], and [math]\left|wz\right|[/math].[br][br]Since we have the proportion: [math]\frac{a\left|z\right|}{a}=\frac{b\left|z\right|}{b}[/math], we can conclude the triangles are similar since two pairs of corresponding sides are proportional and their included angles (the right angles) are congruent.[br][br]This has two implications:[br][list=1][*]The ratio of similitude is [math]\left|z\right|[/math], which means that [math]\left|wz\right|=\left|w\right|\left|z\right|[/math] (this is an alternative to the algebraic proof you did for homework)[/*][*]The angle formed by [math]wz[/math], [math]0[/math] and [math]az[/math] is congruent to [math]Arg\left(w\right)[/math], since they are corresponding angles of similar triangles[/*][/list][br]This leads us to our other conclusion, that [math]Arg\left(wz\right)=Arg\left(z\right)+Arg\left(w\right)[/math][br][br]Key results:[br]ļ»æ[math]\left|wz\right|=\left|w\right|\left|z\right|[/math][br][math]Arg\left(wz\right)=Arg\left(w\right)+Arg\left(z\right)[/math]
Exponential graph as 2-variable function
Drawing a Parabola
Place Points on the graph that are equidistant from F and the given line.
Intersection of a Parabola and a Line
To see how many ways we can intersect a line and a parabola, try adjusting the red line above to see how many times it can meet the blue circle.[br][br]Drag points [math]A[/math] and [math]B[/math] around to change the location and slope of the red line.
What is the maximum number of points of intersection?