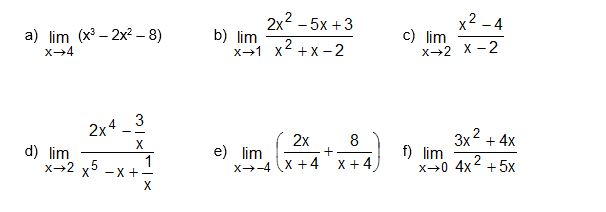[size=100]Stelle die zusammengesetzte Funktion grafisch dar. Untersuche dann die Stellen x = 1 und x = 4.[br][br][br][br][/size]
Grenzwerte für x gegen x0
Wir betrachten folgendes Beispiel:
Übung 1
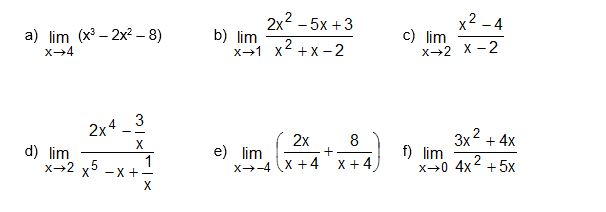
[size=50]Lösungen: a) 24 b) –1/3 c) 4 d) 1 e) 2 f) 4/5[br][br][br][br][/size]
Aufgabe zum Diskutieren
Beurteile mit schlüssiger Begründung, ob die folgenden Aussagen über den Grenzwert einer Funktion wahr oder falsch sind:[br][br][list=1][*]Wenn an einer Stelle x[sub]0 [/sub]sowohl der linksseitige als auch der rechtsseitige Grenzwert existiert, dann existiert der Grenzwert an dieser Stelle x[sub]0[/sub].[/*][*]Wenn der Grenzwert an einer Stelle x[sub]0 [/sub]existiert, dann existiert an dieser Stelle x[sub]0[/sub] sowohl der linksseitige als auch der rechtsseitige Grenzwert.[/*][*]Wenn an einer Stelle x[sub]0 [/sub]sowohl der linksseitige als auch der rechtsseitige Grenzwert existiert und beide gleich gross sind, dann existiert der Grenzwert an dieser Stelle x[sub]0[/sub].[/*][*]Wenn der Grenzwert an einer Stelle x[sub]0 [/sub]nicht existiert, dann existiert an dieser Stelle x[sub]0[/sub] entweder der linksseitige oder der rechtsseitige Grenzwert nicht.[/*][*]Wenn der Grenzwert an einer Stelle x[sub]0 [/sub]existiert, dann ist er gleich gross wie der linksseitige und der rechtsseitige Grenzwert an dieser Stelle x[sub]0[/sub].[/*][*]Wenn die Funktion an der Stelle x[sub]0 [/sub]definiert ist, dann existiert der Grenzwert an dieser Stelle x[sub]0[/sub].[/*][*]Wenn der Grenzwert an einer Stelle x[sub]0 [/sub]existiert, dann ist die Funktion an dieser Stelle x[sub]0[/sub] definiert.[/*][/list][br][size=50]Lösung: wahr: b, c, e[/size][br]