As transformações isométricas estão não apenas na matemática, mas no nosso dia a dia. Podem ser encontradas na natureza, como na simetria do nosso rosto e no rosto de animais, em cristais de gelo ou em folhas ou flores. Nas produções artísticas elas são amplamente usadas, como em mosaicos e azulejos, estampas e tecidos ou na arquitetura. [br]
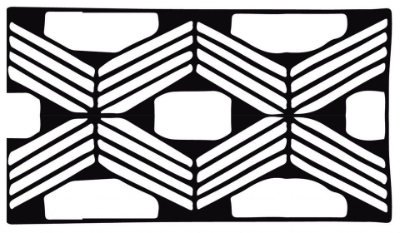
[center]Imagem: Grafismo Indígena. Disponível em: [url=https://commons.wikimedia.org/wiki/File:Grafismo_Ind%C3%ADgena.jpg]https://commons.wikimedia.org/wiki/File:Grafismo_Ind%C3%ADgena.jpg[br][/url][/center]
Vamos analisar algumas produções usando as transformações isométricas.

[center][/center]Imagem: Autor. Produzida no GeoGebra.
[br]1) Qual o único polígono que pode ser usado para criar essa obra?[br]
2) Quais as transformações isométricas usadas para criar essa obra?
3) Quantas foram, no mínimo, as rotações feitas para criar a obra a partir de um único triângulo?[br]
4) Qual o menor ângulo utilizado para rotacionar o triângulo roxo (mais escuro) e chegar no triângulo lilás (mais claro)?
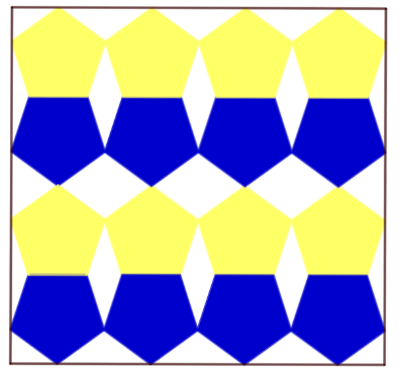
[center][/center]Imagem: Autor. Produzida no GeoGebra.
5) Qual o polígono usado para criar a arte acima?
6) Quais foram as transformações isométricas utilizadas nesse polígono para gerar a obra?[br][br][br]
7) Quantas reflexões, no mínimo, foram utilizadas para criar essa obra?
8) Em matemática, pavimentação (ou ladrilhamento) é a arte de cobrir um plano com polígonos sem deixar espaços ou sobreposições, de modo que as figuras se encaixem perfeitamente e os ângulos em cada vértice somem 360°. O polígono escolhido para essa obra é interessante para se fazer uma pavimentação somente o usando? Justifique.
Na figura, pode-se notar que há partes não preenchidas, pequenas o suficiente para não entrar outro pentágono. Ainda, no pentágono regular, seu ângulo interno é 108° e não é um divisor de 360°.



