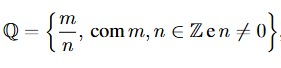
Segmentos comensuráveis
[justify] Consideremos um segmento de reta AB. Para determinar a medida desse segmento, ou seja, a distância entre os pontos A e B, devemos fixar uma unidade de medida padrão u, denominada segmento unitário ou segmento de medida 1. Dividindo o segmento AB em n segmentos justapostos, com (n − 1) pontos interiores, a medida de AB será a soma das medidas desses n segmentos. Caso estes n segmentos sejam todos congruentes a u, então AB = n, isto é, u cabe n vezes em AB.[br][br] Contudo, pode ocorrer de u não caber um número inteiro de vezes em AB. Neste caso, a medida de AB não será dada por um número inteiro positivo, o que conduz à definição de número racional ou fração. Para tanto, consideremos um segmento de reta r que caiba n vezes em u e m vezes em AB. Assim, o segmento r será uma medida comum de u e AB, estes denominados segmentos comensuráveis, isto porque existe uma unidade comum para expressar a medida de ambos. Desta forma, temos que r = [math]\frac{1}{n}[/math] e, consequentemente, AB = [math]\frac{m}{n}[/math].[br][br] Segundo Lima et al. (1997, p. 63): “Quando o segmento considerado é comensurável com a unidade escolhida, sua medida é um número racional (inteiro ou fracionário)”. A figura a seguir ilustra segmentos comensuráveis.[/justify]
[justify] Segmentos não comensuráveis são denominados incomensuráveis. Neste caso, os segmentos não podem ser medidos com base em outra unidade de medida, como ilustra a figura abaixo.[/justify]
A partir da comensurabilidade, pode-se estabelecer o conceito de número racional:[br][br] "Número racional é todo número que pode ser representado por meio de uma fração d= [math]\frac{m}{n}[/math], onde m e n pertencem a [math]\mathbb{Z}[/math], com n[math]\pm[/math]0".[br][br] Por conseguinte, o conjunto dos números racionais [math]\mathbb{Q}[/math] é representado como:
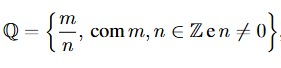
[justify]abrangendo os números naturais ([math]\mathbb{N}[/math]) e os números inteiros ([math]\mathbb{Z}[/math]).[br][br] Nesta perspectiva, é importante destacarmos que existem diversas maneiras de definir os números racionais. De acordo com Charalambous e Pitta-Pantazi (2007 apud Quaresma; Ponte, 2012, p. 40), podemos relacionar cinco significados diferentes para os números racionais:[br][br] (i) parte-todo – caso em que existe uma comparação entre a parte de um todo contínuo ou discreto, ou seja, o número racional representa a relação entre o numerador que indica o número de partes que se tomam do todo e o denominador que é o número de partes em que o todo está dividido, a compreensão deste significado é fundamental para a compreensão dos restantes significados; [br][br] (ii) razão – designa uma comparação entre duas quantidades da mesma natureza ou de natureza distinta;[br][br] (iii) operador – transforma o cardinal de um conjunto discreto, pode ser partitivo (no caso da fração [math]\frac{1}{b}[/math]) ou multiplicativo partitivo (no caso da fração [math]\frac{a}{b}[/math], com a[math]\pm[/math]0);[br][br] (iv) quociente – um número racional visto como resultado de uma divisão entre dois números naturais, onde o numerador e o denominador representam o todo;[br][br] (v) medida – situação que se traduz na comparação entre duas grandezas, em que uma delas é considerada a unidade.[br][br] Assim, um número racional é representado por uma fração, a qual corresponde a um número inteiro ou a um decimal finito ou a uma dízima periódica. Ainda, podemos representar um número racional por meio de recursos gráficos, como ilustrações e retas numéricas. O número racional cinco décimos (que significa a metade de 1 inteiro), por exemplo, pode ser representado pela fração irredutível [math]\frac{1}{2}[/math] e pelo número decimal 0, 5, conforme as figuras abaixo.[/justify]
A origem do Tangram
[justify] O Tangram é um quebra-cabeça muito antigo, de origem chinesa, e cercado por várias lendas sobre seu surgimento. A mais conhecida relata a história de um rei que tinha uma grande paixão por colecionar azulejos. Em determinado momento, ele pediu a um de seus servos que levasse um azulejo como presente para um amigo. No caminho, o servo tropeçou e deixou o azulejo cair, quebrando-o em sete peças: dois triângulos retângulos isósceles grandes, um triângulo retângulo isósceles médio, dois triângulos retângulos isósceles pequenos, um quadrado e um paralelogramo, como ilustra a figura a a seguir. Ao tentar montar novamente o azulejo, o servo percebeu que era possível criar diversas formas utilizando as sete peças (chamadas de "tans"), como animais, objetos, figuras geométricas, entre outras. Por essa razão, o quebra-cabeça passou a ser considerado mágico.[/justify]
O vídeo a seguir, uma animação de Sandra Gobert, ilustra a lenda do Tangram.
A origem do Stomachion
[justify][/justify][justify] O [i]Stomachion[/i], também conhecido como[i] loculus Archimedius[/i] (caixa de Arquimedes), é um dos quebra-cabeças geométricos mais antigos conhecidos, sendo sua invenção atribuída a Arquimedes, o renomado estudioso grego de Siracusa, que viveu no século III a.C. A tradução do termo [i]Stomachion[/i] não é totalmente precisa, mas muitos acreditam que esteja relacionada à palavra "estômago".[/justify]
[justify] Este quebra-cabeça é composto por 14 peças poligonais que se ajustam para formar um quadrado, podendo ser reorganizadas para criar diversas figuras e formas, como ilustra a figura abaixo.[/justify]
[justify] O vídeo de Nayeli (2021), disponível a seguir, traz exemplos de 10 figuras que podem ser formadas utilizando todas as 14 peças do [i]Stomachion[/i].[/justify]
10 figuras con Stomachion cuadrado de Arquimedes - Nayeli
A origem do Disorientation
[justify] Em 2018, a professora de matemática Catriona Shearer, de Cambridge, no Reino Unido, passou a compartilhar no X (antigo Twitter) quebra-cabeças geométricos que ela criava como passatempo. Esses desafios foram solucionados de forma criativa e engenhosa por diversas pessoas.[/justify]
Um desses quebra-cabeças é o[i] Disorientation[/i], ilustrado na figura acima, composto por um triângulo isósceles (verde), um triângulo retângulo (azul) e dois triângulos escalenos ([i]rosê e amarelo[/i]), que juntos compõem um quadrado.
Segmentos incomensuráveis
[justify] Dois segmentos AB e CD são comensuráveis se existir um número x > 0, x ∈ R, tal que: o comprimento de AB é um múltiplo de x, ou seja, |AB| = nx, n ∈ [math]\mathbb{N}[/math]; o comprimento de CD é também um múltiplo de x, isto é, |CD| = mx, m ∈ [math]\mathbb{N}[/math] (Lima, 2013). Contudo, nem sempre o comprimento de um segmento será um múltiplo de x.[br][br] O problema mais sério é que por muito tempo se pensava que dois segmentos quaisquer eram sempre comensuráveis: sejam quais fossem AB e CD, aceitava-se tacitamente que haveria sempre um segmento EF que caberia um número exato n de vezes em AB e um número exato m de vezes em CD. Esta crença talvez adviesse da Aritmética, onde dois números naturais quaisquer têm sempre um divisor comum (na pior hipótese, igual a 1). A ilusão da comensurabilidade durou até o quarto século antes de Cristo (Lima et. al., 1997, p. 53).[br][br] Assim, percebeu-se que “os números naturais mais as frações são insuficientes para medir todos os segmentos de reta” (Lima, 1997, p. 54). Nesse contexto, ficou evidente a necessidade de um outro tipo de número.[br][br] A solução que se impunha, e que foi finalmente adotada, era a de ampliar o conceito de número, introduzindo os chamados números irracionais, de tal modo que, fixando uma unidade de comprimento arbitrária, qualquer segmento de reta pudesse ter uma medida numérica. Quando o segmento considerado é comensurável com a unidade escolhida, sua medida é um número racional (inteiro ou fracionário). Os números irracionais representam medidas de segmentos que são incomensuráveis com a unidade (Lima et. al., 1997, p.54).[br][br] O advento dos números irracionais foi um marco importante na história da matemática, ocorrendo principalmente na Grécia Antiga. Durante esse período, matemáticos como os pitagóricos acreditavam que todos os números podiam ser expressos como razões de dois números inteiros, ou seja, como frações. No entanto, a descoberta de que certas diagonais, como a do quadrado unitário, não podiam ser representadas por frações, revelou a existência de números que não poderiam ser expressos dessa forma. Essa descoberta, atribuída a uma lenda envolvendo o matemático Hipaso de Metaponto, levou ao reconhecimento dos números irracionais. Essa revelação desafiou as 58 concepções tradicionais da época e expandiu significativamente a compreensão dos números, abrindo caminho para o desenvolvimento de uma matemática mais abrangente e sofisticada.[br][br][b] Definição:[/b] Número irracional é todo número que não pode ser escrito/representado como o quociente/razão de dois números inteiros.[br] [br] Os números irracionais, cujo conjunto é simbolizado por I, são representados por meio de expressões decimais infinitas e não periódicas. Esses números também podem ser representados por meio de raízes quadradas ou outras raízes que resultam em valores não racionais, como √2 ou √3. Além disso, alguns números irracionais, como π e o número de Euler e, podem ser expressos por meio de frações contínuas ou usando notação matemática específica. Essas representações ajudam a compreender e trabalhar com esses números em diferentes contextos, especialmente na Geometria e na Análise Matemática, onde aparecem frequentemente em medidas e proporções que não podem ser expressas exatamente por números racionais.[br][br] A existência de segmentos incomensuráveis aponta para a insuficiência dos números naturais e das frações para medir qualquer segmento de reta. Como definir então o comprimento da diagonal do quadrado de lado 1? A solução encontrada pelos matemáticos foi ampliar o conceito de número e introduzir os chamados números irracionais (Broetto, 2016, p. 48-49).[br][br][b] Teorema: [/b]A medida da diagonal de um quadrado é um número irracional.[/justify]
A origem do Trinity Quartet
[justify] Em seu blog MathWithBadDrawings, [url=https://mathhombre.tumblr.com/post/615493545429696512/shearers-geometry-puzzles]https://mathhombre.tumblr.com/post/615493545429696512/shearers-geometry-puzzles[/url], Ben Orlin republicou alguns quebra-cabeças geométricos semelhantes a sangaku, dentre eles o Trinity Quartet, ilustrado na figura abaixo. Este [i]puzzle[/i] é composto por quatro triângulos equiláteros e dois pares de triângulos escalenos congruentes. Os oito triângulos formam um quadrado de dimensões [math]2a[/math] x [math]\frac{4\sqrt{3}}{3}a[/math].[/justify]
[justify] O termo sangaku, ou "tábua matemática" ou "tábua de cálculo", refere-se aos quebra-cabeças geométricos japoneses, tipicamente esculpidos em tábuas de madeira e exibidos em templos ou santuários, especialmente durante o período Edo (ou Tokugawa, período da história japonesa que vai de 1603 a 1868). Essas "tábuas matemáticas" frequentemente apresentavam formas e relações geométricas intrincadas, criando desafios para os espectadores resolverem. [/justify]
Composição de imagens
[justify] No aplicativo abaixo estão as 33 peças dos quatro quebra-cabeças explorados neste livro digital: Tangram, [i]Stomachion[/i] de Arquimedes, [i]Disorientation[/i] e[i] Trinity Quartet[/i]. Use sua criatividade para compor uma obra de arte com todas essas peças.[/justify]
Sua arte
Referências
[justify][/justify]AMBROZI, L. [b]Jogos em uma sequência didática para o ensino de análise combinatória[/b]. 162 f. Dissertação (Mestrado Profissional em Ensino de Ciências e Matemática) – Programa de Pós‑Graduação em Ensino de Ciências e Matemática, Universidade de Caxias do Sul, Caxias do Sul, 13 nov. 2017. Disponível em: <[url=https://repositorio.ucs.br/xmlui/bitstream/handle/11338/3450/Dissertacao%20Luiz%20Ambrozi.pdf?sequence=1&isAllowed=y]https://repositorio.ucs.br/xmlui/bitstream/handle/11338/3450/Dissertacao%20Luiz%20Ambrozi.pdf?sequence=1&isAllowed=y[/url]>. Acesso em: 22 jul. 2025.[br][br]BELOZERSKY. [b]Concepto de educación moderna. Iconos científicos y portátil con los libros voladores en el fondo. Libros electrónicos, cursos en Internet y proceso de graduación. [/b]Rússia: Shutterstock, 2018. Disponível em: <[url=https://www.shutterstock.com/es/image-vector/modern-education-concept-science-icons-laptop-1113998933]https://www.shutterstock.com/es/image-vector/modern-education-concept-science-icons-laptop-1113998933[/url]>. Acesso em: 12 jun. 2025.[br][br]BO, A. [b]Espiral pitagórica[/b]. 2021. Disponível em: <[url=https://commons.wikimedia.org/wiki/File:Espiral_pitag%C3%B3rica.png]https://commons.wikimedia.org/wiki/File:Espiral_pitag%C3%B3rica.png[/url]>. Acesso em: 16 jul. 2025.[br][br]BRACHI, L. [b]Stomachion. [/b][S. l.]: Instagram, 2022. Disponível em: <[url=https://www.instagram.com/linobrachi/]https://www.instagram.com/linobrachi/[/url]>. Acesso em: 01 mar. 2025.[br][br]BRASIL. [b]Base Nacional Comum Curricular.[/b] Brasília: MEC/SEB/CNE, 2018. Disponível em: <[url=https://www.gov.br/mec/pt-br/escola-em-tempointegral/BNCC_EI_EF_110518_versaofinal.pdf]https://www.gov.br/mec/pt-br/escola-em-tempointegral/BNCC_EI_EF_110518_versaofinal.pdf[/url]>. Acesso em: 22 out. 2024.[br][br]BROETTO, G. C. [b]O ensino de números irracionais para alunos ingressantes na Licenciatura em[br]Matemática.[/b] 588 f. Tese (Doutorado) — Universidade Federal do Espírito Santo, Espírito Santo,[br]2016. Disponível em: <[url=https://repositorio.ufes.br/items/95872f04-6c3b-4e51-a1bf-cd9fa2529113]https://repositorio.ufes.br/items/95872f04-6c3b-4e51-a1bf-cd9fa2529113[/url]>. Acesso em: 13 jan. 2025.[br][br]CAMPUZANO, J. C. P. [b]Script: Pythagoras tree[/b] [arquivo GeoGebra]. GeoGebra, 2025. Disponível em: <[url=https://www.geogebra.org/m/verprw5j]https://www.geogebra.org/m/verprw5j[/url]>. Acesso em: 17 jul. 2025.[br][br]CAVALCANTE, R. [b]A classificação dos números relacionada ao cotidiano.[/b] [S. l.]: Tic na Matemática, 2014. Disponível em: <[url=https://www.ticsnamatematica.com/2014/08/classificacao-numeros-cotidiano.html]https://www.ticsnamatematica.com/2014/08/classificacao-numeros-cotidiano.html[/url]>.[br]Acesso em: 15 jun. 2025.[br][br]FAURE, S. [b]Pythagoras tree[/b] [arquivo GeoGebra]. GeoGebra, [s. d.]. Disponível em <[url=https://www.geogebra.org/m/UpR5U8fM]https://www.geogebra.org/m/UpR5U8fM[/url]>. Acesso em: 17 jul. 2025.[br][br]FERREIRA, T. [b]Metodologia da matemática lúdica: o uso do Tangram como recurso de atividade.[/b] São Paulo: Linkedin, 2016. Disponível em: <[url=https://pt.linkedin.com/pulse/metodologia-da-matem%C3%A1tica-l%C3%BAdica-o-uso-do-tangram-como-ton-ferreira]https://pt.linkedin.com/pulse/metodologia-da-matem%C3%A1tica-l%C3%BAdica-o-uso-do-tangram-como-ton-ferreira[/url]>. Acesso em: 7 fev. 2025.[br][br]FIGUEIREDO, E. B. de. [b]FAB3D – Laboratório Fábrica Matemática.[/b] Joinville: UDESC, 2025. Disponível em: [br]<[url=https://www.printables.com/@Fab3DUdesc_403051]https://www.printables.com/@Fab3DUdesc_403051[/url]>. Acesso em: 10 jul. 2025.[br][br]GAROFALO, D. [b]5 motivos para usar games na aula de Matemática[/b]. [S. l.]: Nova Escola, 2017. Disponível em: <[url=https://novaescola.org.br/conteudo/6776/5-motivos-para-usar-games-na-aula-de-matematica]https://novaescola.org.br/conteudo/6776/5-motivos-para-usar-games-na-aula-de-matematica[/url]>. Acesso em: 20 fev. 2025. [br][br]GAUCI, J. B. [b]The mathematics of Euclid, Archimedes and Apollonius. [/b][S. l.]: Times of Malta, 2018. Disponível em: <[url=https://timesofmalta.com/article/The-mathematics-of-Euclid-Archimedes-and-Apollonius.669144]https://timesofmalta.com/article/The-mathematics-of-Euclid-Archimedes-and-Apollonius.669144[/url]>. Acesso em: 16 fev. 2025.[br][br]GIOVANNI JÚNIOR, J. [b]A conquista matemática: 6º ano.[/b] 1a. ed. São Paulo: FTD, 2022.[br][br]GOBERT, S. [b]A lenda do Tangram e as sete peças mágicas.[/b] [S. l.]: Youtube, 2022. Disponível em: <[url=https://www.youtube.com/watch?v=I-RxCw_QdV0]https://www.youtube.com/watch?v=I-RxCw_QdV0[/url]>. Acesso em: 07 fev. 2025. [br][br]GONÇALVES, W. V. [b]Espiral Pitagórica[/b]. GeoGebra, 2020. Disponível em: < [url=https://www.geogebra.org/m/rduacrtg]https://www.geogebra.org/m/rduacrtg[/url] >. Acesso em: 16 jul. 2025.[br][br]GOUVEIA, R. [b]Números Irracionais.[/b] [S. l.]: Toda Matéria, [s. d.]. Disponível em: <[url=https://www.todamateria.com.br/numeros-irracionais/]https://www.todamateria.com.br/numeros-irracionais/[/url]>. Acesso em: 7 fev. 2025.[br][br]GUERBER, C. W. [b]Usando puzzles, origami e tecnologias digitais do estudo de frações, números irracionais e áreas na educação básica. [/b]144 f. Dissertação (Mestrado) — Universidade Tecnológica Federal do Paraná, Curitiba, Paraná, 2025. Disponível em: <https://repositorio.utfpr.edu.br/jspui/handle/1/38300>. Acesso em: 17 set. 2025.[br][br]LIMA, E. [b]Números racionais.[/b] [S. l.]: Matematicando, 2015. Disponível em:<[url=https://matematicando.net.br/numeros-racionais/]https://matematicando.net.br/numeros-racionais/[/url]>. Acesso em: 09 jul. 2025.[br][br]LIMA, E. L. [b]Números e funções reais.[/b] Rio de Janeiro: SBM, 2013.[br][br]LIMA, E. L. et al. [b]A matemática do Ensino Médio. [/b]v. 1. Rio de Janeiro: SBM, 1997.[br][br]MMA. [b]Números Racionais x Números Irracionais[/b]. MMA das Exatas, 2025. Disponível em: <[url=https://mmadasexatas.com.br/numeros-racionais-x-numeros-irracionais/]https://mmadasexatas.com.br/numeros-racionais-x-numeros-irracionais/[/url]>. Acesso em: 16 jul. 2025.[br][br]NAYELI. [b]10 figuras con Stomachion cuadrado de Arquimedes - Nayeli[/b]. [S. l.]: Youtube, 2020. Disponível em: <[url=https://www.youtube.com/watch?v=J3M2UVAJKTY]https://www.youtube.com/watch?v=J3M2UVAJKTY[/url]>. Acesso em: 07 fev. 2025.[br][br]NCTM. [b]Archimedes’ puzzle.[/b] [S. l.]: National Council of Teachers of Mathematics, 2008. Disponível em: [br]<[url=https://illuminations.nctm.org/uploadedFiles/Content/Lessons/Resources/3-5/Stomachion-AS-ArchPuzzle.pdf]https://illuminations.nctm.org/uploadedFiles/Content/Lessons/Resources/3-5/Stomachion-AS-ArchPuzzle.pdf[/url]>. Acesso em: 03 mar. 2025.[br][br]OPENAI. [i]Imagem (ilustração digital) gerada pelo ChatGPT com a mensagem “De 17.152 maneiras diferentes!”[/i]. Disponível em: <[url=https://chatgpt.com/s/m_688417990c2c81919761d045a24a3a59]https://chatgpt.com/s/m_688417990c2c81919761d045a24a3a59[/url]>. Acesso em: 25 jul. 2025.[br][br]ORLIN, B. [b]11 geometry puzzles that drive mathematicians to madness. [/b][S. l.]: Math with bad drawings, 2020. Disponível em: <[url=https://mathwithbaddrawings.com/2020/04/15/11-geometry-puzzles-that-drive-mathematicians-to-madness/]https://mathwithbaddrawings.com/2020/04/15/11-geometry-puzzles-that-drive-mathematicians-to-madness/[/url]>. Acesso em: 07 fev. 2025. [br][br]PACHECO, A. [b]Incomensurabilidade.[/b] Atractores, 2021. Disponível em: <[url=https://www.atractor.pt/mat/incomensurabilidade/]https://www.atractor.pt/mat/incomensurabilidade/[/url]>. Acesso em: 25 jul. 2025.[br][br]QUARESMA, M.; PONTE, J. P. da. Compreensão dos números racionais, comparação e ordenação: o caso de Leonor.[b] Revista Interações[/b], v. 8, n. 20, p. 37–69, 2012. Disponível em: <[url=https://revistas.rcaap.pt/interaccoes/article/view/485]https://revistas.rcaap.pt/interaccoes/article/view/485[/url]>. Acesso em: 14 jan. 2025.[br][br]SAITO, O. H. [b]Construção de puzzles geométricos com origami[/b]. [S. l.: s. n.], 2025.[br][br]SANTOS, T. E. [b]Você já ouviu falar sobre o Tangram? [/b][S. l.]: Escola Web, [s. d.]. Disponível em: <[url=https://escolaweb.educacao.al.gov.br/roteiro-de-estudo/voce-ja-ouviu-falar-sobre-o-tangram-56115]https://escolaweb.educacao.al.gov.br/roteiro-de-estudo/voce-ja-ouviu-falar-sobre-o-tangram-56115[/url]>. Acesso em: 07 fev. 2025.[br][br]SHEARER, C. [b]Catriona Agg.[/b] [S. l.]: X, 2025. Disponível em: <[url=https://x.com/cshearer41]https://x.com/cshearer41[/url]>. Acesso em: 08 fev. 2025.[br][br]SHEARER, C. [b]Geometry puzzles in felt tip: a compilation of puzzles from 2018.[/b] [S. l.]: Amazon, 2019. Disponível em: <[url=https://www.amazon.com/Geometry-Puzzles-Felt-Tip-compilation-ebook/dp/B07RRJNVYR]https://www.amazon.com/Geometry-Puzzles-Felt-Tip-compilation-ebook/dp/B07RRJNVYR[/url]>. Acesso em: 16 fev. 2025.[br][br]SHUTTERSTOCK. [b]Ilustraciones de fichas bibliográficas[/b]. [S. l.]: Shutterstock, 2025. Disponível em: <[url=https://www.shutterstock.com/es/search/fichas-bibliogr%C3%A1ficas?image_type=illustration]FichasBibliográficas: Maisde 178 Ilustrações e DesenhosLicenciados Royalty-Free |Shutterstock[/url]>. Acesso em: 15 jun. 2025.[br][br]SILVA, F. [b]Stomachion de Arquimedes - curiosidades#02. [/b][S. l.]: Youtube, 2022. Disponível em < [url=https://www.youtube.com/watch?v=ohBetshibEA]https://www.youtube.com/watch?v=ohBetshibEA[/url]>. Acesso em: 07 fev. 2025. [br][br]SILVA, J. S. [b]Você sabe resolver porcentagem? [/b][S. l.]: Quizur, 2024. Disponível em: <[url=https://pt.quizur.com/trivia/voce-sabe-resolver-porcentagem-1nZ11#google_vignette]VocêSabe Resolver[br]Porcentagem| JOCILDA DOS SANTOS SILVA | Quizur[/url]>. Acesso em: 15 jun. 2025.[br][br]SODRÉ, U. [b]Números racionais. [/b]Londrina: Matemática essencial: Ensino Fundamental, Médio e Superior no Brasil, 2020. Disponível em: <[url=https://www.uel.br/projetos/matessencial/basico/fundamental/racionais.html]https://www.uel.br/projetos/matessencial/basico/fundamental/racionais.html[/url]>. Acesso em: 14 jan. 2025.[br][br]SÓESCOLA. [b]Cards de números com Tangram[/b]. [S. l.: s. n.], 2017. Disponível em:<[url=https://soescola.com/2017/03/cards-de-numeros-com-tangra.html#google_vignette]https://soescola.com/2017/03/cards-de-numeros-com-tangra.html#google_vignette[/url]>. Acesso em: 01 mar. 2025.[br][br]TYMOFIEIEVA, N. [b]Volta às aulas. Feche frações de madeira coloridas sobre a mesa. Matemática na pré-escola e na escola[/b]. [S. l]: Istockphoto, 2023. Disponível em: <[url=https://www.istockphoto.com/br/foto/volta-%C3%A0s-aulas-feche-fra%C3%A7%C3%B5es-de-madeira-coloridas-sobre-a-mesa-matem%C3%A1tica-na-pr%C3%A9-gm1846143157-551642789]FotodeVolta ÀsAulas Feche Frações De Madeira Coloridas Sobre A Mesa Matemática NaPréescolaENa Escola e mais fotos de stock de Sinal de fração - iStock[/url]>. Acesso em: 15 jun. 2025.[br][br]WIKIPÉDIA. [b]Árvore de Pitágoras.[/b] Disponível em: <[url=https://pt.wikipedia.org/wiki/%C3%81rvore_de_Pit%C3%A1goras]https://pt.wikipedia.org/wiki/%C3%81rvore_de_Pit%C3%A1goras[/url]>. Acesso em: 16 jul. 2025.[br]
