[size=150][size=100][b]A particle starts from a fixed point O and moves along a straight line. After t seconds, its displacement,s is given by s=t[sup]3[/sup]-3t[sup]2[/sup]-4t. Calculate[/b][b][br]a) the initial acceleration, in ms[/b][sup]-2[/sup][b], of the particle,[/b][b][br]b) instantaneous acceleration of the particle, in ms[/b][sup]-2[/sup][b] , after 5 seconds,[/b][b][br]c) the acceleration of the particle,in ms[/b][sup]-2[/sup][b], when it passes through the fixed point O again,[/b][b][br]d) the range of values of t, in seconds,when the acceleration of the particle is positive[/b][/size][/size]

[size=150][size=100][color=#ff0000][b]Solution[/b][br][/color][/size][/size]

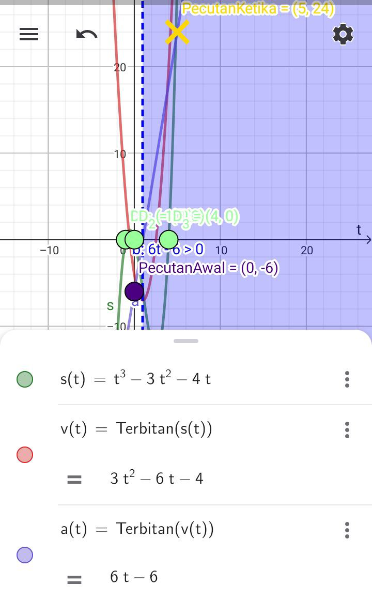
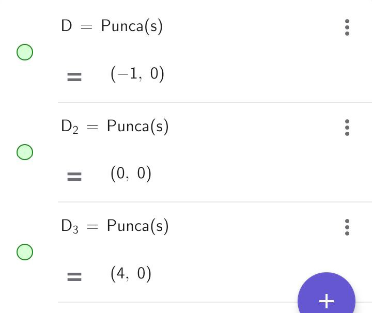
[size=150][size=100]Given the displacement function, s=t[sup]3[/sup]-3t[sup]2[/sup]-4t.[br]Then, the velocity function v=[math]\frac{ds}{dt}[/math]=3t[sup]2[/sup]-6t- 4 and acceleration function, a=[math]\frac{dv}{dt}[/math]=6t-6.[br][br]a) When t=0,a=6(0)-6=-6ms[sup]-2[/sup][br] Hence, the initial acceleration is -6ms[sup]-2[/sup] .[br][/size][br][size=100]b) When t=5,a=6(5)-6=24ms[sup]-2[/sup][br] Hence, the instantaneous acceleration at 5 seconds is 24 ms[sup]-2[/sup] .[br][/size][br][size=100]c) When the particle passes through the fixed point O again,[br] s=0[br] t[sup]3[/sup]-3t[sup]2[/sup]-4t=0[br] t(t[sup]2[/sup]-3t-4)=0[br] t(t-4)(t+1)=0[br] t=0,t=4,t=-1(rejected)[br] When t=4,a=6(4)-6=18ms[sup]-2 [/sup][br] Hence, when the particle passes through fixed point O again, the acceleration is 18 ms[sup]-2 [/sup]when t=4s[i].[br][/i][/size][br][/size][size=50][size=150][size=100]d)[/size][/size][size=150][size=100]For the acceleration to be positive, [br] a>0[br] 6t-6>0[br] 6t>6[br] t>1 [br] Hence, the acceleration would be positive when t>1.[/size][/size][/size][br]