รวบรวมบทเรียน การใช้โปรแกรม GeoGebra
บทเรียนการใช้โปรแกรม GeoGebra
Table of Contents
- การใช้เครื่องมือเรขาคณิตพลวัต
- 1. การใช้เครื่องมือเรขาคณิตพลวัต (1) (Version 2)
- 2. การใช้เครื่องมือเรขาคณิตพลวัต (2) (Version 2)
- 3. การใช้เครื่องมือเรขาคณิตพลวัต (3) (Version 2)
- 4. การใช้เครื่องมือเรขาคณิตพลวัต (4) (Version 2)
- 5. การใช้เครื่องมือเรขาคณิตพลวัต (5) (Version 2)
- 6. การใช้เครื่องมือเรขาคณิตพลวัต (6) (Version 2)
- 7. การใช้เครื่องมือเรขาคณิตพลวัต (7) (Version 2)
- 8. การใช้เครื่องมือเรขาคณิตพลวัต (8) (Version 2)
- 9. การใช้เครื่องมือเรขาคณิตพลวัต (9) (Version 2)
- การใช้ระบบพีชคณิตคอมพิวเตอร์
- 10. ระบบพีชคณิตคอมพิวเตอร์ (1) (Version 2)
- 11. ระบบพีชคณิตคอมพิวเตอร์ (2) (Version 2)
- 12. ระบบพีชคณิตคอมพิวเตอร์ (3) (Version 2)
- การเชื่อมโยงระหว่าง DGS และ CAS
- 13. การเชื่อมโยงระหว่าง DGS และ CAS (1) (Version 2)
- 14. การเชื่อมโยงระหว่าง DGS และ CAS (2) (Version 2)
- คุณสมบัติอื่น ๆ ของโปรแกรม GeoGebra
- 15. คุณสมบัติอื่น ๆ ของโปรแกรม GeoGebra (1) (Version 2)
- 16. คุณสมบัติอื่น ๆ ของโปรแกรม GeoGebra (2) (Version 2)
- 17. คุณสมบัติอื่น ๆ ของโปรแกรม GeoGebra (3) (Version 2)
- 18. คุณสมบัติอื่น ๆ ของโปรแกรม GeoGebra (4) (Version 2)
1. การใช้เครื่องมือเรขาคณิตพลวัต (1) (Version 2)
ชื่อ - สกุล รหัสประจำตัวนิสิต (4 ตัวท้าย) กลุ่มผู้เรียน
เช่น นายวีริศ กิตติวรากูล 0500 SC4ED1
จุดประสงค์การเรียนรู้
เพื่อให้นิสิตครูสามารถใช้เครื่องมือเรขาคณิตพลวัตในการสร้างเกี่ยวกับจุด ส่วนของเส้นตรง เส้นตรง และรังสีได้
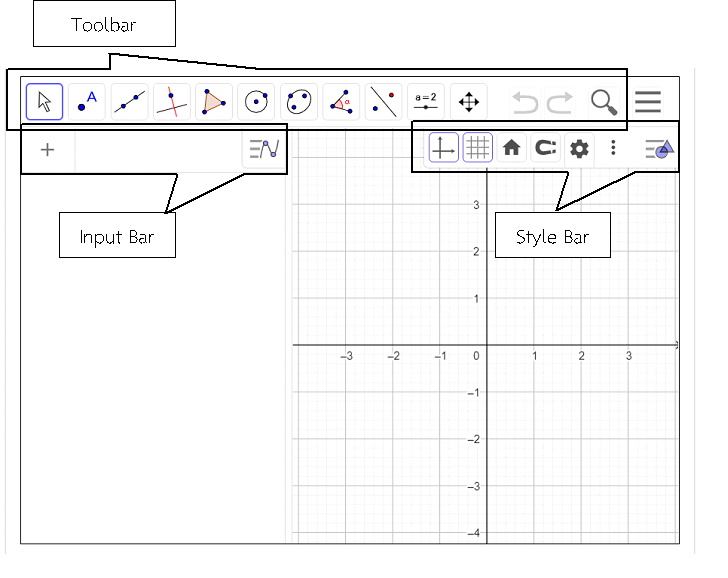
แนะนำหน้าต่างของโปรแกรม GeoGebra
เมื่อเปิดโปรแกรม GeoGebra จะพบหน้าต่างและมีส่วนประกอบดังต่อไปนี้
1. การใช้เครื่องมือในการสร้างจุด
[b]ความรู้ทางคณิตศาสตร์ที่เกี่ยวข้อง[br][/b]- จุด (Point) ในทางเรขาคณิต เป็นคำอนิยาม (Undefined Terms)[br][b][br]วิธีการใช้เครื่องมือในการสร้างจุด[/b][br]1) คลิกปุ่ม [img]https://wiki.geogebra.org/uploads/thumb/a/a9/Mode_point.svg/24px-Mode_point.svg.png[/img] เลือก Point [img]https://wiki.geogebra.org/uploads/thumb/a/a9/Mode_point.svg/24px-Mode_point.svg.png[/img][br]2) คลิกตำแหน่งใด ๆ ในชิ้นงานเพื่อกำหนดตำแหน่งของจุด A[br]3) จะได้ จุด A ซึ่งเป็น[b]อ็อบเจกต์อิสระ[/b] (ไม่มีตัวแม่ และตัวลูก เพราะการสร้างจุดเราสามารถสร้างลงไปในชิ้นงานได้ โดยที่ไม่ต้องขึ้นอยู่กับวัตถุอื่นใดในชิ้นงาน)[br][b]หมายเหตุ[/b] : การสร้างจุดบนแผ่นงาน สามารถ Input ด้วยคำสั่งในรูป[br] <ชื่อจุด>(<พิกัด X>,<พิกัด Y>)
ให้นิสิตสร้างจุดสองจุด (ชื่ออะไรก็ได้ ตำแหน่งใดก็ได้) ใน Applet ด้านล่างนี้
2. การแสดงชื่อของอ็อบเจกต์
1) คลิกปุ่ม [img]https://wiki.geogebra.org/uploads/thumb/8/83/Mode_move.svg/22px-Mode_move.svg.png[/img] เพื่อออกจากการการทำงานการสร้างใด ๆ ทั้งหมด[br]ในกรณีเปลี่ยนชื่อ[br]2) คลิกขวาที่อ็อบเจกต์ที่ต้องการเปลี่ยนชื่อ แล้วคลิก Rename[br]3) พิมพ์ชื่อของอ็อบเจกต์ที่ต้องการแล้วกด OK[br]ในกรณีต้องการซ่อน/แสดง ชื่อของอ็อบเจกต์[br]4) คลิกขวาที่อ็อบเจกต์ที่ต้องการซ่อน/แสดง ชื่อของอ็อบเจกต์ เลือก Show Label[br][br][b][u]เทคนิคเพิ่มเติม[/u][/b][br]กรณีต้องการให้ชื่อเป็นตัวห้อย เช่น [math]A_1[/math] ให้พิมพ์ชื่อเป็น A_{1} ในตอนที่ Rename
3. การใช้เครื่องมือในการสร้างส่วนของเส้นตรง
[b]ความรู้ทางคณิตศาสตร์ที่เกี่ยวข้อง[br][/b]- [b]ส่วนของเส้นตรง[/b] (Segment) คือ[u]ส่วนหนึ่ง[/u]ของเส้นตรงที่มี[b][i][u]จุดปลายสองจุด[/u][/i][/b]
จากบทนิยามของส่วนของเส้นตรง ท่านคิดว่าในการสร้างส่วนของเส้นตรงต้องมีการกำหนดการสร้างให้[b][u]ขึ้นอยู่กับอ็อบเจกต์ใด[/u][/b] (ตัวแม่)
[b]วิธีการใช้เครื่องมือในการสร้างส่วนของเส้นตรง[/b][br]1) คลิกปุ่ม [img]https://wiki.geogebra.org/uploads/thumb/e/e3/Mode_join.svg/24px-Mode_join.svg.png[/img] ตามด้วย segment [icon]https://www.geogebra.org/images/ggb/toolbar/mode_segment.png[/icon][br]2) คลิกตำแหน่งใด ๆ ในชิ้นงาน เพื่อกำหนดตำแหน่งของจุด A ซึ่งเป็นจุดปลายจุดหนึ่งของส่วนของเส้นตรงที่ต้องการสร้าง[br]3) คลิกตำแหน่งใด ๆ ในชิ้นงานอีกครั้ง เพื่อกำหนดตำแหน่งของจุด B ซึ่งเป็นจุดปลายอีกจุดหนึ่งของส่วนของเส้นตรงที่ต้องการสร้าง[br]4) จะได้ส่วนของเส้นตรง f ซึ่งมีจุด A และจุด B เป็นจุดปลายของส่วนของเส้นตรง[br][b]หมายเหตุ[/b] : การสร้างส่วนของเส้นตรง สามารถ Input ด้วยคำสั่งในรูป[br] Segment(<จุดปลาย>,<จุดปลาย>)[br][br][b]เทคนิคเพิ่มเติม:[/b][br]หากต้องการให้โปรแกรม GeoGebra แสดงชื่อเฉพาะในส่วนของจุดเวลาสร้างส่วนของเส้นตรง หรืออ็อบเจกต์อื่น ๆ ในครั้งถัดไป ให้ทำตามขั้นตอนต่อไปนี้[br]1) เลือก Menu (รูปสามขีดมุมบนขวาของ Applet)[br]2) เลือก Settings[br]3) ในส่วนของ Labelling ให้ปรับเป็น New Points Only
ให้นิสิตสร้างส่วนของเส้นตรงที่มี P และ Q เป็นจุดปลาย โดยซ่อนชื่อที่ปรากฏบนตัวเส้นใน Applet ด้านล่างนี้
จาก Applet ข้างต้น ให้นิสิตเลื่อนจุด P แล้วสำรวจว่า เมื่อเลื่อนจุด P แล้ว มีวัตถุใดที่เปลี่ยนแปลงตำแหน่งนอกจากจุด P หรือไม่
จากผลการตอบคำถามข้างต้น เราจะเรียกจุด P และจุด Q ว่า "ตัวแม่"[br]และเรียกส่วนของเส้นตรง f ว่า "ตัวลูก"[br]สังเกตว่า ตัวแม่ เป็นสิ่งที่จำเป็น ในการสร้างอ็อบเจกต์ที่เป็นตัวลูก[br]กล่าวคือ ถ้าไม่มีจุดปลายสองจุด จะไม่สามารถสร้างส่วนของเส้นตรงได้ ซึ่งสอดคล้่องกับบทนิยามของส่วนของเส้นตรงนั่นเอง
4. การใช้เครื่องมือสร้างเส้นตรง
[b]ความรู้ทางคณิตศาสตร์ที่เกี่ยวข้องกับเส้นตรง[/b][br]- [b]เส้นตรง[/b] (Line) เป็นคำอนิยาม[br]- [b]สัจพจน์ที่เกี่ยวข้องกับเส้นตรง[/b] มีเส้นตรง[u]เพียงเส้นเดียวเท่านั้น[/u]ที่ผ่านจุดที่ลากผ่าน[u]จุดที่กำหนดให้ 2 จุด[/u]ได้
จากแนวคิดเกี่ยวกับเส้นตรงข้างต้น ท่านคิดว่าในการสร้างเส้นตรงต้องมีการกำหนดการสร้างให้[b][u]ขึ้นอยู่กับอ็อบเจกต์ใด[/u][/b] (ตัวแม่)
[b]วิธีการสร้างเส้นตรง[/b][br]1. คลิกปุ่ม [img]https://wiki.geogebra.org/uploads/thumb/e/e3/Mode_join.svg/24px-Mode_join.svg.png[/img] ตามด้วย Line [icon]https://www.geogebra.org/images/ggb/toolbar/mode_join.png[/icon][br]2. คลิกตำแหน่งใด ๆ ในชิ้นงาน เพื่อกำหนดตำแหน่งของจุด A ซึ่งเป็นจุดหนึ่งที่เส้นตรงผ่าน[br]3. คลิกตำแหน่งใด ๆ ในชิ้นงานอีกครั้ง เพื่อกำหนดตำแหน่งของจุด B ซึ่งเป็นอีกจุดหนึ่งที่เส้นตรงผ่าน[br]4. จะได้เส้นตรง f ซึ่งมีจุด A และจุด B เป็นจุดที่เส้นตรงผ่าน[br][b]หมายเหตุ[/b] : การสร้างเส้นตรง สามารถ Input ด้วยคำสั่งในรูป[br] Line(<จุดที่ผ่าน>,<จุดที่ผ่าน>)[br][br][b]เทคนิคเพิ่มเติม[br][/b]สามารถเปลี่ยนสีและลักษณะการแสดงผลของอ็อบเจกต์ โดยการเลือกอ็อบเจกต์ที่ต้องการ แล้วใช้เครื่องมือต่าง ๆ บน Style Bar ซึ่งปรากฏด้านบนขวาของ Applet
ให้เลื่อนอ็อบเจกต์ต่าง ๆ ใน Applet ข้างต้น ได้แก่ จุด A จุด B และเส้นตรง f แล้วตอบคำถาม
ข้อใดต่อไปนี้เป็นตัวแม่บ้าง
5. การใช้เครื่องมือสร้างรังสี
[b]ความรู้ทางคณิตศาสตร์ที่เกี่ยวข้องกับรังสี[/b][br]- [b]รังสี[/b] (Ray) คือ ส่วนหนึ่ง[u]ของเส้นตรง[/u]ที่มี[u]จุดปลายเพียงจุดเดียว[br][br][/u][u][b]หมายเหตุ[/b][/u] รังสีเป็นส่วนหนึ่งของเส้นตรง และจากสัจพจน์เกี่ยวกับเส้นตรง (มีเส้นตรงเพียงเส้นเดียวเท่านั้นที่ลากผ่านจุดสองจุดที่กำหนดให้) ทำให้ได้ว่า การกำหนดรังสีนั้นจะต้องมีจุดปลาย และจุดที่รังสีผ่าน เพื่อให้สามารถลากเป็นเส้นตรงได้
จากแนวคิดเกี่ยวกับรังสีข้างต้น ท่านคิดว่าในการสร้างรังสีต้องมีการกำหนดการสร้างให้[b][u]ขึ้นอยู่กับอ็อบเจกต์ใด[/u][/b] (ตัวแม่)
[b]วิธีการสร้างรังสี[/b][br]1. คลิกปุ่ม [img]https://wiki.geogebra.org/uploads/thumb/e/e3/Mode_join.svg/24px-Mode_join.svg.png[/img] ตามด้วย Ray [icon]https://www.geogebra.org/images/ggb/toolbar/mode_ray.png[/icon][br]2. คลิกตำแหน่งใด ๆ ในชิ้นงาน เพื่อกำหนดตำแหน่งของจุด A ซึ่งเป็นจุดปลายของรังสี[br]3. คลิกตำแหน่งใด ๆ ในชิ้นงานอีกครั้ง เพื่อกำหนดตำแหน่งของจุด B ซึ่งเป็นจุดที่รังสีผ่าน[br]4. จะได้รังสี f ซึ่งมีจุด A เป็นจุดปลายและจุด B เป็นจุดที่รังสีผ่าน[br][b]หมายเหตุ[/b] : การสร้างรังสี สามารถ Input ด้วยคำสั่งในรูป[br] Ray(<จุดปลาย>,<จุดที่ผ่าน>)
ให้เลื่อนอ็อบเจกต์ต่าง ๆ ใน Applet ข้างต้น ได้แก่ จุด P จุด Q และรังสี f แล้วตอบคำถาม
ข้อใดต่อไปนี้เป็นตัวแม่บ้าง
10. ระบบพีชคณิตคอมพิวเตอร์ (1) (Version 2)
ชื่อ - สกุล รหัสนิสิต 3 ตัวท้าย
เช่น นายวีริศ กิตติวรากูล 500
จุดประสงค์การเรียนรู้
เพื่อให้นิสิตครูสามารถใช้ระบบพีชคณิตคอมพิวเตอร์ในการแก้ปัญหาทางคณิตศาสตร์ได้
1. การคำนวณหาผลลัพธ์พื้นฐานของระบบพีชคณิตคอมพิวเตอร์
[b]การดำเนินการและฟังก์ชันในการคำนวณที่ควรทราบ มีดังนี้[/b][br]1) การดำเนินการบวก ลบ คูณ และหาร ให้ใช้แป้นพิมพ์ +, -, * และ / ในการ input ตามลำดับ[br]2) การหา ห.ร.ม. ของจำนวน n จำนวน สามารถ input ด้วยคำสั่ง GCD(<จำนวนที่ 1>,<จำนวนที่ 2>, ...,<จำนวนที่ n>)[br]3) การหา ค.ร.น. ของจำนวน n จำนวน สามารถ input ด้วยคำสั่ง LCM(<จำนวนที่ 1>,<จำนวนที่ 2>, ...,<จำนวนที่ n>)[br]4) การตรวจสอบจำนวนเฉพาะ สามารถ input ด้วยคำสั่ง isprime(<จำนวน>)[br]5) การดำเนินการยกกำลัง ให้ใช้แป้นพิมพ์ ^ ในการ input[br]6) การหากรณฑ์ที่สอง สามารถ input ด้วยคำสั่งในรูป sqrt(<จำนวน>)[br]7) การหารากที่ n สามารถ input ด้วยคำสั่งในรูป nroot(<จำนวน>,<รากที่ n>)[br]8) การหาค่าสัมบูรณ์ สามารถ input ด้วยคำสั่งในรูป abs(<จำนวน>)[br]9) การหาค่าของฟังก์ชันลอการิทึม สามารถ input ด้วยคำสั่งดังต่อไปนี้[br] - [math]log_bx[/math] input ด้วยคำสั่ง log(<ฐานของลอการิทึม>,<จำนวน>)[br] - [math]ln\left(x\right)[/math] input ด้วยคำสั่ง ln(<จำนวน>)[br] หมายเหตุ : ค่าคงตัว e ใน CAS ให้กดแป้นพิมพ์ Alt + e เนื่องจากกรณีที่ผู้ใช้พิมพ์ e โปรแกรมจะมองเป็นตัวแปรตัวแปรหนึ่ง[br]10) การหาค่าของฟังก์ชันตรีโกณมิติ สามารถ input ด้วยคำสั่งดังต่อไปนี้[br] - [math]sin\left(x\right)[/math] input ด้วยคำสั่ง sin()[br] - [math]cos\left(x\right)[/math] input ด้วยคำสั่ง cos()[br] - [math]tan\left(x\right)[/math] input ด้วยคำสั่ง tan()[br] - [math]cosec\left(x\right)[/math] input ด้วยคำสั่ง cosec() (ใช้ csc แทน cosec ได้)[br] - [math]sec\left(x\right)[/math] input ด้วยคำสั่ง sec()[br] - [math]cot\left(x\right)[/math] input ด้วยคำสั่ง cot()[br] หมายเหตุ : - ค่าคงตัว [math]\pi[/math] ให้พิมพ์ว่า pi[br] - หากต้องการคำนวณหน่วยองศา ให้ใช้ Virtual Keyboard ในการใส่สัญลักษณ์ [math]^{\circ}[/math] ประกอบ เช่น sin(30[math]^\circ[/math])[br]11) การหาค่าของตัวผกผันของฟังก์ชันตรีโกณมิติ สามารถ input ด้วยคำสั่งต่อไปนี้[br] - [math]arcsin\left(x\right)[/math] input ด้วยคำสั่ง arcsin(<จำนวน>) (ใช้ asin แทน arcsin ได้)[br] - [math]arccos\left(x\right)[/math] input ด้วยคำสั่ง arccos(<จำนวน>) (ใช้ acos แทน arccos ได้)[br] - [math]arctan\left(x\right)[/math] input ด้วยคำสั่ง arctan(<จำนวน>) (ใช้ atan แทน arctan ได้)[br]12) การกำหนดเวกเตอร์ [math]xi+yj[/math] หรือ [math]xi+yj+zk[/math] สามารถ input ด้วยคำสั่ง vector(<ค่า x>,<ค่า y>) หรือ vector(<ค่า x>,<ค่า y>,<ค่า z>)[br]13) การกำหนดจำนวนเชิงซ้อน สัญลักษณ์ของส่วนจินตภาพ i ให้กดแป้นพิมพ์ Alt + i[br]14) การหาค่าของแฟคทอเรียล สามารถพิมพ์สัญลักษณ์ "!" หลังจำนวนได้เลย เช่น 5!
จงใช้ Applet ระบบพีชคณิตคอมพิวเตอร์ หรือ Algebra แสดงการคำนวณในแต่ละแถวดังต่อไปนี้
Row 1. [math]1+2-3.5\times4\div\left(2.17+4.93\right)[/math][br]Row 2. [math]\sqrt{78996544}-\sqrt[3]{470366406433}+99^2[/math] [br]Row 3. [math]log\left(200\right)+log\left(5\right)-log_{sqrt\left(2\right)}4+e^{ln\left(2021\right)}-9![/math][br]Row 4. [math]sin^2\left(\frac{2564\pi}{3}\right)+arccos\left(-\frac{\sqrt{3}}{2}\right)[/math][br]Row 5. [math]\left|9i-12j\right|+\left|-24i+10j\right|[/math]
ให้พิมพ์แสดงการคำนวณในแต่ละแถวให้ถูกต้อง
2. Symbolic Evaluation และ Numeric Evaluation
[u][b]Symbolic Evaluation[/b][br][/u]- เป็นการคำนวณผลลัพธ์ให้แสดงออกมาอยู่ในรูปสัญลักษณ์ (คำตอบเป็นเศษส่วน หรืออยู่ในเครื่องหมายกรณฑ์)[br]- สามารถปรับคำตอบให้แสดงผลแบบ Symbolic Evaluation โดยการคลิกปุ่ม [icon]/images/ggb/toolbar/mode_evaluate.png[/icon] ใน Row ที่ต้องการให้เปลี่ยนการแสดงผล[br][br][u][b]Numeric Evaluation[/b][br][/u]- เป็นการคำนวณผลลัพธ์ให้แสดงออกมาอยู่ในรูปตัวเลขเท่านั้น (คำตอบเป็นทศนิยม ไม่มีสัญลักษณ์เศษส่วน หรือเครื่องหมายกรณฑ์)[br]- สามารถปรับคำตอบให้แสดงผลแบบ Numeric Evaluation โดยการคลิกปุ่ม [icon]/images/ggb/toolbar/mode_numeric.png[/icon] ใน Row ที่ต้องการให้เปลี่ยนการแสดงผล[br][br][b][u]การปรับการแสดงผลจำนวนตำแหน่งของทศนิยม[br][/u][/b]1) เปิดหน้าต่าง Settings[br]2) ปรับ Rounding ให้เป็นจำนวนตำแหน่งของทศนิยมตามที่ต้องการ
จงใช้ระบบพีชคณิตคอมพิวเตอร์[br]1) แสดงค่าประมาณของ [math]\sqrt{2}[/math] ถึงทศนิยมตำแหน่งที่ 15 ใน Row 1[br]2) แสดง 0.5 ในรูปของเศษส่วน (แสดงผลลัพธ์เป็น [math]\frac{1}{2}[/math]) ใน Row 2
3. การกำหนดค่าของตัวแปร
[b][u]การกำหนดค่าของตัวแปร[/u][/b][br]ถ้าต้องการกำหนดตัวแปร a ให้มีค่าเป็น 1 ให้ป้อน input เป็น a := 1 แล้วกด Enter จะทำให้ระบบจำว่า a มีค่าเท่ากับ 1[br][br][u][b]การยกเลิกการกำหนดค่าของตัวแปร[/b][br][/u]ให้ลบ Row ที่มีการกำหนดค่า a ออก จะทำให้ a กลับไปเป็นตัวแปรเหมือนเดิม
4. ระบบพีชคณิตคอมพิวเตอร์กับตัวแปรชนิดจำนวนและบูลีน
[b][u]1) การแก้สมการ[/u][/b] โดยใช้ฟังก์ชัน solve[br] เช่น Input: solve(x+2=5)[br] ผลลัพธ์: {x=3}[br] Input: solve(a^2+3a+2=0,a)[br] ผลลัพธ์: {a=-2, a=-1}[br][br][b][u]2) การจัดนิพจน์ให้อยู่ในรูปอย่างง่าย[/u][/b] โดยใช้ฟังก์ชัน simplify หรือ expand[br] เช่น Input: simplify((x+1)^2))[br] ผลลัพธ์: [math]x^2+2x+1[/math][br] Input: expand(1/sqrt(2))[br] ผลลัพธ์: [math]\frac{\sqrt{2}}{2}[/math][br][br][b][u]3) การแยกตัวประกอบของจำนวนเต็ม หรือพหุนาม [/u][/b]สามารถ input โดยใช้ฟังก์ชัน factor[br] เช่น Input: factor(10}[br] ผลลัพธ์: [math]2\cdot5[/math][br] Input: factor(x^2-5x+6}[br] ผลลัพธ์: (x-3)(x-2)[br][br][b][u]4) ตัวดำเนินการทางตรรกศาสตร์ [/u][/b]ให้ใช้ Virtual Keyboard ดังนี้[br] [math]\wedge[/math] หมายถึง "และ"[br] [math]\vee[/math] หมายถึง "หรือ"[br] [math]\longrightarrow[/math] หมายถึง "ถ้า ... แล้ว"[br] เช่น Input: true [math]\longrightarrow[/math]false[br] ผลลัพธ์: false[br][br][b][u]5) การกำหนดฟังก์ชัน[br][/u][/b] เช่น Input: f(x):=2x+1[br] ผลลัพธ์: กำหนดฟังก์ชัน f เป็น f(x)=2x+1[br] Input: f(x):=if(x<0,-1,1)[br] ผลลัพธ์: กำหนดฟังก์ชัน f โดยนิยามดังนี้[br] [math]f\left(x\right)=\begin{matrix}-1\quad;x<0\\1\quad;x\ge0\end{matrix}[/math][br][br][b][u]6) การหาลิมิตของฟังก์ชัน[/u][br][/b] 1) limit(<ฟังก์ชัน>,<ค่าที่เข้าใกล้>) /* สำหรับการหาลิมิต */[br] 2) limitbelow(<ฟังก์ชัน>,<ค่าที่เข้าใกล้>) /* สำหรับการหาลิมิตซ้าย */[br] 3) limitabove(<ฟังก์ชัน>,<ค่าที่เข้าใกล้>) /* สำหรับการหาลิมิตขวา */ [br][br][b][u]*7) การหาอนุพันธ์ของฟังก์ชัน [/u][/b]โดยใช้ฟังก์ชัน derivative ซึ่ง input ในรูป[br] - derivative(<ฟังก์ชัน>,<ตัวแปร>) หรือ กรณีที่หาอนุพันธ์อันดับสูง ให้แทนค่า input เป็น[br] - derivative(<ฟังก์ชัน>,<ตัวแปร>,<อันดับของอนุพันธ์>)[br] เช่น[br] Input: derivative(3x^4-2/3x^3+5x-1)[br] ผลลัพธ์: [math]12x^3-2x^2+5[/math][br] Input: derivative(x^2-1,x,2)[br] ผลลัพธ์: 2[br][br] ตัวอย่างการหาอนนุพันธ์เมื่อมีการแทนค่าตัวแปร x[br] Input: g(x)=derivative(x^2,x)[br] g(1)[br] ผลลัพธ์: 2 [br] [br][b][u]*8) การหาปริพันธ์ของฟังก์ชัน [/u][/b]โดยใช้ฟังก์ชัน integral ซึ่ง input ในรูป[br] - integral(<ฟังก์ชัน>,<ตัวแปร>) /* กรณีหาปริพันธ์ไม่จำกัดเขต */[br] - integral(<ฟังก์ชัน>,<ตัวแปร>,<ขอบล่าง>,<ขอบบน>) /* กรณีหาปริพันธ์จำกัดเขต */[br] เช่น Input: integral(sqrt(x),x)[br] ผลลัพธ์: [math]\frac{2}{3}\sqrt{x}\cdot x+c_1[/math][br] Input: integral(x,x,x=0,x=1)[br] ผลลัพธ์: [math]\frac{1}{2}[/math][br][br][b]* [u]หมายเหตุ[/u][/b] การใส่ฟังก์ชันในการหาอนุพันธ์ให้เขียนเฉพาะส่วนของตัวแปร x เท่านั้น เช่น ต้องการหาอนุพันธ์ของ [math]y=x^2-5x+4[/math] ให้ input ฟังก์ชันเป็น [math]x^2-5x+4[/math] เท่านั้น
จงใช้ระบบพีชคณิตคอมพิวเตอร์หาคำตอบในแต่ละต่อไปนี้
Row 1. แก้สมการ [math]arcsin\left(tan\left(x\right)\right)=\frac{\pi}{2}[/math][br]Row 2. แยกตัวประกอบของพหุนาม [math]x^4+2x^3+x^2-1[/math][br]Row 3. หาค่าความจริงของประพจน์ [math]T\longrightarrow F[/math][br] (เมื่อ T แทนประพจน์ที่มีค่าความจริงเป็นจริง และ F แทนประพจน์ที่มีค่าความจริงเป็นเท็จ)[br]Row 4. หาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง [math]y=x^2[/math] กับแกน X จาก x = 1 ถึง x = 2[br]Row 5. หาอนุพันธ์[u]อันดับสอง[/u]ของ [math]y=\sqrt{x^2+1}[/math] เมื่อ x = 0
13. การเชื่อมโยงระหว่าง DGS และ CAS (1) (Version 2)
ชื่อ - สกุล รหัสประจำตัวนิสิต 3 ตัวท้าย
เช่น นายวีริศ กิตติวรากูล 500
จุดประสงค์การเรียนรู้
เพื่อให้นิสิตครูสามารถใช้การเชื่อมโยงระหว่างเครื่องมือเรขาคณิตพลวัต และระบบพีชคณิตคอมพิวเตอร์ในการเขียนกราฟของความสัมพันธ์ได้
1. หน้าต่างของโปรแกรม GeoGebra
หน้าต่างของโปรแกรม GeoGebra มีดังนี้[br] 1) Algebra - ใช้ในการแสดงผลว่าในชิ้นงานมีอ็อบเจกต์หรือตัวแปรอะไรบ้าง และสามารถ input ในลักษณะของ CAS ในหน้าต่างนี้ได้เช่นเดียวกัน[br] 2) CAS - ระบบพีชคณิตคอมพิวเตอร์[br] 3) Graphics - ใช้สำหรับการแสดงผลอ็อบเจกต์[br] 4) Graphics 2 - ใช้สำหรับการแสดงผลอ็อบเจกต์[br] 5) 3D Graphics - ใช้สำหรับการแสดงผลเชิงอ็อบเจกต์แบบสามมิติ[br] 6) Spreadsheet - ตารางการทำงาน[br] 7) Probability Calculator - ใช้ในการคำนวณเกี่ยวกับการแจกแจงความน่าจะเป็นแบบต่าง ๆ และการทดสอบสมมติฐานทางสถิติ[br] 8) Construction Protocol - ใช้ตรวจสอบขั้นตอนการสร้าง และสมบัติของแต่ละอ็อบเจกต์ในชิ้นงาน[br] ซึ่งสามารถเลือกเปิดหรือปิดแต่ละหน้าต่างตามการใช้งานได้ โดยคลิกปุ่ม ที่มีไอคอนเป็นรูปจุดสามจุด ซึ่งอยู่ใน Style bar ด้านขวาของปุ่ม Settings
2. การตั้งค่าการแสดงพิกัด และตาราง
คลิกขวาในพื้นที่ว่างชองหน้าต่าง Graphics จะพบเมนูที่น่าสนใจดังนี้[br]- Show Axes เปิด / ปิด แกน X และแกน Y[br]- Show Grid ตั้งค่าการแสดงตารางในระบบพิกัด[br]- x Axis : y Axis ปรับอัตราส่วนของพิกัด X ต่อพิกัด Y[br][br]คลิกขวาในพื้นที่ว่างของหน้าต่าง Graphics เลือก Settings จะพบเมนูดังนี้[br]- เมนู Basic สามารถตั้งค่าต่ำสุด / สูงสุด ของ X และ Y ที่จะแสดงผลใน Graphics ได้ ปรับลักษณะของแกน ขนาดตัวอักษร และสีพื้นหลังได้ เป็นต้น[br]- เมนู xAxis และ yAxis ใช้สำหรับตั้งค่าลักษณะของแกน X และแกน Y ตามลำดับ[br]- เมนู Grid ใช้สำหรับตั้งค่าลักษณะของเส้นตารางในหน้าต่าง Graphics[br] ในเมนู Grid สามารถตั้งค่าการ snap จุดที่ลงได้ โดยให้ตั้งค่า Point Capturing เป็น Snap to Grid หรือ Fixed to Grid
3. การเขียนกราฟของความสัมพันธ์
สามารถทำได้โดยการใส่สมการที่ต้องการเขียนกราฟ (ในรูปของตัวแปร x และตัวแปร y) ในช่อง input ของหน้าต่าง Algebra แล้วกด Enter จะปรากฏกราฟของสมการในหน้าต่าง Graphics
Task 1:
1. ในหน้าต่าง Algebra ให้ input y = x^2 สังเกตผลที่เกิดขึ้นในหน้าต่าง Graphics[br]2. ในหน้าต่าง Algebra ให้ input function(y = -x^2+8, -2, 2) สังเกตผลที่เกิดขึ้นในหน้าต่าง Graphics[br]3. ในหน้าต่าง Algebra ให้ input A:=sequence((a, 2*a), a, -5, 5) สังเกตผลที่เกิดขึ้นในหน้าต่าง Graphics
Task 2:
จงเขียนกราฟ และตั้งชื่อกราฟดังต่อไปนี้ในหน้าต่าง Graphics[br] 1) [math]f_1:y=sin\left(x\right)[/math] โดยที่ [math]x\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right][/math][br] 2) [math]f_2:y=arcsin\left(x\right)[/math][br] 3) [math]r_1:\left(x-5\right)^2+\left(y-5\right)^2=9[/math][br] 4) [math]r_2:y=-4[/math] โดยที่ [math]x\in\left[-5,5\right][/math][br] 5) [math]P:y=-2x[/math] โดยที่ [math]x\in\left\{-5,-4,-3,...,3,4,5\right\}[/math]
Task 3: การเขียนกราฟแบบพลวัต
1. ในหน้าต่าง Graphics สร้างสไลเดอร์แทนตัวแปรชนิดจำนวน ดังต่อไปนี้[br] 1) a มีค่าระหว่าง -5 ถึง 5[br] 2) h มีค่าระหว่าง -10 ถึง 10[br] 3) k มีค่าระหว่าง -10 ถึง 10[br]2. ในหน้าต่าง Algebra ให้ input y=a(x-h)^2+k[br]3. ปรับค่าในสไลเดอร์ a, h และ k แล้วสังเกตการเปลี่ยนแปลงของลักษณะกราฟที่เกิดขึ้น
Task 4:
ให้เขียนกราฟแบบพลวัตของสมการวงรี ซึ่งมีรูปมาตรฐานดังนี้[br] [math]\frac{\left(x-h\right)^2}{a^2}+\frac{\left(y-k\right)^2}{b^2}=1[/math]
15. คุณสมบัติอื่น ๆ ของโปรแกรม GeoGebra (1) (Version 2)
ชื่อ - สกุล รหัสประจำตัวนิสิต 3 ตัวท้าย
เช่น นายวีริศ กิตติวรากูล 500
จุดประสงค์การเรียนรู้
เพื่อให้นิสิตครูสามารถใช้กล่องข้อความในการพิมพ์ด้วย LaTeX formula และสร้างข้อความแบบพลวัตได้
1. การพิมพ์ข้อความด้วย LaTeX formula
LaTeX formula เป็นรูปแบบการพิมพ์ข้อความที่รองรับสัญลักษณ์ทางคณิตศาสตร์ต่าง ๆ ซึ่งสามารถทำได้ดังนี้[br]1) คลิกปุ่ม [icon]/images/ggb/toolbar/mode_slider.png[/icon] เลือก Text[br]2) คลิกที่ว่างในชิ้นงานจะปรากฏกล่องข้อความขึ้น[br]3) คลิก Advanced เลือก LaTeX formula[br]4) ฟังก์ชันพื้นฐานในการพิมพ์โดยใช้ LaTeX formula ที่ควรทราบมีดังนี้[br] \ หมายถึง เคาะวรรค[br] \quad หมายถึง tab[br] \\ หมายถึง เว้นบรรทัด[br] \<สี>{<ข้อความ>} หมายถึง ใส่สีสำหรับข้อความ[br] เช่น \blue{ABC} จะแสดงคำว่า "ABC" เป็นสีน้ำเงิน[br] \underline{<ข้อความ>} หมายถึง ขีดเส้นใต้ข้อความ[br] \bold{<ข้อความ>} หมายถึง ทำให้ข้อความเป็นตัวหนา[br]5) การพิมพ์สัญลักษณ์ทางคณิตศาสตร์อื่น ๆ สามารถคลิกดูได้ที่ปุ่ม [math]\alpha\beta\gamma[/math] และปุ่ม LaTeX formula ที่อยู่ใต้คำว่า Advanced
2. ข้อความแบบพลวัต (Dynamic Text)
[b][u]2.1 การทำให้ข้อความมีการแสดงผลตามตัวแปร[/u][/b] สามารถทำได้ดังตัวอย่างต่อไปนี้[br][br][size=100][size=150]Task 2:[/size][/size][b][br]สถานการณ์:[/b] มีตัวแปรจำนวนจริง a และ b อยู่ในช่วง 0 ถึง 5 ต้องการแสดงข้อความในรูปแบบ[br] <ค่าของ a> บวกด้วย <ค่าของ b> เท่ากับ <ค่าของ a+b>[br] ตัวอย่างเช่น กรณีที่ a = 2 และ b = 3 จะแสดงผลลัพธ์เป็น "2 บวกด้วย 3 เท่ากับ 5"[br][br][b][u]ขั้นตอนการสร้าง[/u][/b][br]1) กำหนดตัวแปร a และ b (ในกรณีนี้สมมติให้เป็นจำนวนจริงบนสไลเดอร์)[br]2) ในหน้าต่าง Algebra ให้ input c:=a+b[br]3) คลิกปุ่ม [icon]https://www.geogebra.org/images/ggb/toolbar/mode_slider.png[/icon] เลือก Text[br]4) คลิกที่ว่างในชิ้นงานจะปรากฏกล่องข้อความขึ้น[br]5) คลิก Advanced แล้วคลิกปุ่ม [icon]/images/ggb/toolbar/mode_conic5.png[/icon] แล้วเลือกตัวแปร a[br]6) พิมพ์คำว่า "บวกด้วย"[br]7) เลือกตัวแปร b[br]8) พิมพ์คำว่า "เท่ากับ"[br]9) เลือกตัวแปร c[br]10) คลิก Preview เพื่อตรวจสอบการแสดงผลของข้อความ แล้วคลิก OK[br]11) จะได้ข้อความตามต้องการ สำรวจการเปลี่ยนแปลงของข้อความโดยปรับสไลเดอร์ค่า a และ b
Task 3:
ให้สร้างสไลเดอร์เพื่อรับตัวแปรสองตัวแปรได้แก่ a และ b ซึ่งเป็นจำนวนจริงในช่วง [0, 10][br]และสร้างกล่องข้อความเพื่อแสดงผลดังนี้[br][quote]พื้นที่ของรูปสี่เหลี่ยมมุมฉาก = <ค่าของ a> [math]\times[/math] <ค่าของ b> = <ค่าของ a [math]\times[/math] b>[/quote]ตัวอย่างเช่น ถ้า a = 2 และ b = 3 จะแสดงผลเป็น[br][quote]พื้นที่ของรูปสี่เหลี่ยมมุมฉาก = 2 [math]\times[/math] 3 = 6[/quote]
2.2 การตรึงข้อความกับจุด
การตรึงข้อความกับจุดสามารถทำได้ดังตัวอย่างกิจกรรมใน Task 3 ดังนี้
Task 4:
[b]สถานการณ์ :[/b] จาก Applet ด้านล่างนี้ ต้องการให้แสดงข้อความที่จุด A ว่า[br][quote]ระยะห่างระหว่างจุด O และจุด A เท่ากับ <ค่าของระยะห่าง> [/quote][b][u]ขั้นตอนการสร้าง[/u][/b][br]1. สร้างข้อความ text1 ซึ่งเป็นข้อความแบบพลวัตให้แสดงผลดังนี้[br][quote]ระยะห่างระหว่างจุด O และจุด A เท่ากับ <ค่าของระยะห่าง>[/quote]2. คลิกเลือกข้อความ text1 แล้วคลิกที่ Settings[br]3. เลือกเมนู Position ปรับตรง Starting Point ให้เป็น A[br]4. จะได้ว่าข้อความ text1 จะเปลี่ยนตำแหน่งตามจุด A สามารถปรับตำแหน่งของข้อความรอบ ๆ จุด A ได้ตามความเหมาะสม
3. การตรึงตำแหน่งของอ็อบเจกต์ในหน้าจอ และการล็อกอ็อบเจกต์
[u][b]การตรึงตำแหน่งของอ็อบเจกต์ในหน้าจอ[/b][br][/u]- ช่วยไม่ให้อ็อบเจกต์เคลื่อนที่ เมื่อผู้ใช้ทำการเลื่อนตำแหน่ง หรือซูมเข้าหรือซูมออกในชิ้นงาน[br]- ใช้ได้เฉพาะกับอ็อบเจกต์ที่ไม่เกี่ยวข้องกับตำแหน่งของพิกัดในชิ้นงาน เช่น ข้อความ ปุ่ม และสไลเดอร์เป็นต้น[br]- สามารถทำได้โดยคลิกเลือกอ็อบเจกต์ที่ต้องการตรึงตำแหน่งในหน้าจอ แล้วคลิกปุ่ม Pin to Screen ใน Style bar หรือคลิกขวา แล้วเลือก Pin to Screen[br][br][u][b]การล็อกอ็อบเจกต์[/b][br][/u]- ช่วยไม่ให้อ็อบเจกต์เคลื่อนที่ ถึงแม้ผู้ใช้จะคลิกเลือกอ็อบเจกต์นั้นแล้วก็ตาม[br]- สามารถทำได้โดยการคลิกที่อ็อบเจกต์ที่ต้องการล็อก แล้วคลิกปุ่ม Lock Object ใน Style bar หรือ คลิกขวา แล้วเลือก Lock Object
4. การเลือกแสดงผล Graphics แบบ 2 หน้าต่าง
ในกรณีที่ชิ้นงานที่มีความจำเป็นต้องแสดงผลมากกว่า 1 หน้าต่าง ผู้ใช้สามารถกำหนดอ็อบเจกต์ให้แสดงในหน้าต่างใดหน้าต่างหนึ่ง หรือทั้ง 2 หน้าต่างพร้อมกันก็ได้ดังนี้
Task 5:
สถานการณ์ [b]:[br] [/b]พิจารณา Applet ด้านล่างนี้ จะเห็นว่าประกอบด้วยอ็อบเจกต์ 3 อย่าง ได้แก่ 1) ข้อความ "Graphics 1" 2) ข้อความ Graphics 2 และ 3) ข้อความ Graphics 1 & Graphics 2[br] ต้องการปรับการแสดงผลดังนี้[br] 1) ข้อความ "Graphics 1" แสดงในหน้าต่าง Graphics 1 เท่านั้น[br] 2) ข้อความ "Graphics 2" แสดงในหน้าต่าง Graphics 2 เท่านั้น[br] 3) ข้อความ "Graphics 1 & 2" แสดงทั้งในหน้าต่าง Graphics 1 และ Graphics 2[br][br][b][u]ขั้นตอน[br][/u][/b]1) Graphics 1 แสดงผลในหน้าต่าง Graphics 1 ถูกต้องแล้ว จึงไม่ต้องดำเนินการใด ๆ[br]2) คลิกเลือกข้อความ Graphics 2 คลิก Settings ไปที่เมนู Advanced แล้วเลือก Graphics 2 อย่างเดียวเท่านั้น[br]3) คลิกเลือกข้อความ Graphics 1 & 2 คลิก Settings ไปที่เมนู Advanced แล้วเลือก Graphics 1 และ Graphics 2