Matematik Öğretim Teknolojileri Final Ödevi
a[math]\ne[/math]0 ve a, b [math]\epsilon[/math][math]\mathbb{R}[/math] olmak üzere f : [math]\mathbb{R}\longrightarrow\mathbb{R},f\left(x\right)[/math][math]=ax^2+bx+c[/math] şeklindeki fonksiyona[b] [i][color=#ff0000]ikinci dereceden [br]bir değişkenli fonksiyon [/color][/i][/b]denir.[br][math]f[/math] =[math][/math]{[math]\left(x,y\right)[/math]|[math]y=ax^2+bx+c[/math], [math][/math][math]a\ne0[/math]ve [math]a,b,c[/math] [math]\epsilon\mathbb{R}[/math]} kümesinin elemanları olan ( x, y) ikililerine analitik düzlemde karşılık gelen noktaların oluşturduğu grafiğe [b][i][color=#ff0000]parabol [/color][/i][/b]denir.[br]a>0 ise grafiğin kolları şekildeki gibi yukarı doğrudur. a<0 ise grafiğin kolları şekildeki gibi aşağı doğrudur.[br][br]• a[math]\ne[/math]0, a, b, c [math]\epsilon\mathbb{R}[/math] olmak üzere [math]f:[/math][math]\mathbb{R}\longrightarrow\mathbb{R}[/math],[math]f[/math]([math]x[/math])=[math]ax^2+bx+c[/math] olsun.[br]Bir parabolün artanlıktan azalanlığa ya da azalanlıktan artanlığa geçtiği noktasına [b][i][color=#ff0000]tepe noktası[/color][/i][/b][br]denir. Tepe noktası T(r,k) olduğuna göre, r=-[math]\frac{b}{2a}[/math] ve k=[math]f[/math](r)=[math]f[/math]=(-[math]\frac{b}{2a}[/math])=[math]\frac{4ac-b^2}{4a}[/math] olur. [br]• Tepe noktası T(r,k) ise grafiğin şekline göre[b] [color=#ff0000]en büyük ya da en küçük[/color][/b] değeri k’dir. [br]• Grafiğin tepe noktasından geçen x=-[math]\frac{b}{2a}[/math] doğrusuna parabolün[i][color=#ff0000] [b]simetri ekseni [/b][/color][/i]denir.[br][br]r [math]\epsilon[/math][m,n], f: [m,n][math]\longrightarrow\mathbb{R}[/math], f(x)=[math]ax^2+bx+c[/math] fonksiyonunun tepe noktası T(r,k) olmak üzere ;[br]•r [math]\notin[/math][m,n] ise f(m) ve f(n) değerlerinden büyük olan fonksiyonun[i][color=#ff0000] [b]en büyük değeri, küçük [br]olan fonksiyonun en küçük değeridir[/b].[/color][/i][br]•r[math]\epsilon[/math] [m,n] ise f(r), f(m) ve f(n) değerlerinden[i][color=#ff0000][b] küçük olan en küçük değer, büyük olan en [br]büyük değerdir[/b].[/color][/i][br][br] a[math]\ne[/math]0 ve a, b, c [math]\epsilon[/math][math]\mathbb{R}[/math] olmak üzere f(x)=[math]ax^2+bx+c[/math] parabolünün tepe noktası [br]T(r,k) iken f(x)=[math]a.\left(x-r\right)^2+k[/math] şeklinde de yazılabilir.[br] a[math]\ne[/math] a, b, c [math]\epsilon\mathbb{R}[/math] için f(x)=[math]ax^2+bx+c[/math] parabolünün x eksenini kestiği noktaların [br]apsisleri [math]x_1[/math]ve [math]x_2[/math] olmak üzere f(x)=[math]a.\left(x-x_1_{ }\right).\left(x-x_2\right)[/math] şeklinde de yazılabilir.[br][br]y=[math]ax^2+bx+c[/math] parabolü ile y=[math]mx+n[/math] doğrusu verilmiş olsun. (x,y) parabol ile doğrunun [br]ortak bir noktasıysa her iki denklemi de sağlamalıdır. Her iki denklemi sağlayan x değerini bulmak [br]için denklemler [math]ax^2+bx+c=mx+n[/math] biçiminde eşitlenir. Elde edilen[br][math]ax^2+\left(b-m\right)x+c-n=0[/math]ikinci derece denklemin diskriminantı [math]\Delta[/math] olsun.[br][color=#0000ff][b]1.)[/b] [/color][math]\Delta[/math]<0 ise parabol ile [br]doğru[b] [color=#ff0000][i]kesişmez[/i][/color][/b][color=#ff0000][i].[/i][/color][br][color=#0000ff][b]2.)[/b][/color] [math]\Delta[/math]=0 ise parabol ile [br]doğru [b][color=#ff0000]yalnız bir noktada[/color][/b] [br]kesişir.[br][b][color=#0000ff]3.)[/color] [/b][math]\Delta[/math]>0 ise parabol ile doğru [br]farklı [color=#ff0000][b]iki noktada[/b] [/color]kesişir.
[size=150][color=#ff0000][center][b]ETKİNLİK YAPALIM![/b][/center][br][br][/color][/size][justify][size=100][math]\Longrightarrow[/math] Yırtıcı kuş Woody gökyüzünde süzülürken Minik kuşu av olarak gözüne kestirmiştir. Yırtıcı kuş minik kuşun kaçışı sebebiyle parabolik bir yol izleyecektir. Minik kuş parabolik yolun en büyük yada en küçük değer aldığı noktadadır. .Bunu fark eden belgesel çekim ekibinden John olayı kameraya almak amacıyla drone'nu şekilde gösterilen noktaya yerleştirmiştir. John olayı görüntüleyebilmek için drone'nu y ekseni boyunca hareket ettirecektir. Sizce John olayı hangi nokta veya noktalarda olayı gözlemleyebilir?[br][br][br][/size][/justify]
[center][color=#ff0000][b][size=200][size=150]SORULARLA PEKİŞTİRELİM![/size][/size][/b][/color][/center]
SORU-1

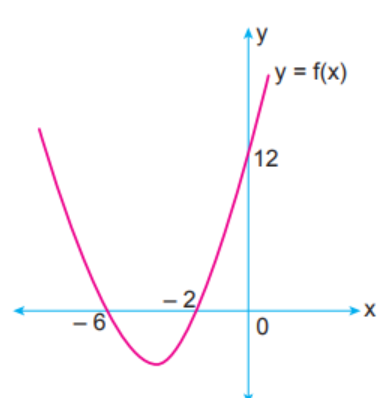
Şekilde gerçek sayılar kümesi üzerinde tanımlı [math]f\left(x\right)=ax^2+bx+c[/math][math][/math] fonksiyonunun grafiği verilmiştir.[br][b]Buna göre,[br][/b]I. a+b=10[br]II. a.c=12[br]III. f(a)=21[br][b]ifadelerinden hangileri doğrudur?[/b]
SORU-2
[size=150][math]y=-x^2+3x+k[/math] parabolü ile [math]y=x-2[/math] doğrusu birbirine teğet olduğuna göre k değeri kaçtır ?[/size]
SORU-3
[size=150]Gerçek sayılar kümesi üzerinde bir f fonksiyonu [br][math]f\left(x\right)=x^2-2x-24[/math] biçiminde tanımlanıyor.[br][br][b]Buna göre,[/b][br]I. f fonksiyonunun grafiğinin x eksenini kestiği noktalar arasındaki uzaklık 10 birimdir.[br]II. f fonksiyonunun en küçük değeri -25'tir.[br]III. f fonksiyonunun grafiğinin simetri ekseni x=5 doğrusudur.[br][b]ifadelerinden hangileri doğrudur?[/b][/size]
SORU-4
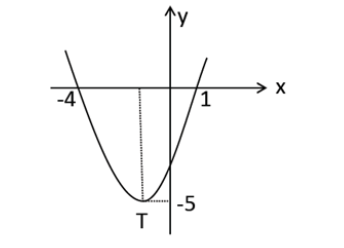
[size=150]Dik koordinat düzleminde tepe noktası T olan bir parabol verilmiştir.[br][br][b]Buna göre fonksiyonun alabileceği [u]en küçük [/u]değer kaçtır?[/b][/size]
SORU-5
[size=150]m ve n sıfırdan farklı birer gerçek sayı olmak üzere, gerçek sayılar kümesi üzerinde bir f fonksiyonu [br][math]f\left(x\right)=mx^2+nx-2m[/math] biçiminde tanımlanıyor.[br][br][b]Buna göre f fonksiyonunun grafiği için aşağıdakilerden hangisi[u] kesinlikle [/u]doğrudur?[/b][/size]
[size=150][b][center][color=#ff0000]1-ALIŞTIRMA YAPALIM![/color][/center][/b][br]Aşağıda y=f(x) parabolünün grafiği verilmiştir. Grafikten yola çıkarak verilen kutucuklara cevaplarınızı yazınız. [br]Cevaplarınızı kontrol etmek için cevap kutucuklarını kullanınız.[/size]
[center][color=#ff0000][b][/b][/color][/center][color=#ff0000][b][center][size=150]2-ALIŞTIRMA YAPALIM![/size][/center][/b][/color]