Tutoriel - Étape 03 - Patron pyramide régulière à base carrée

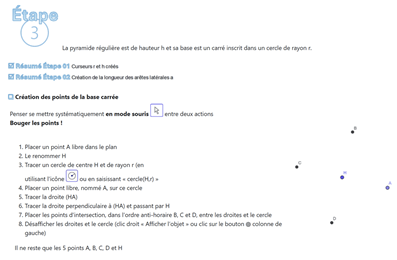
[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJEAAACCCAYAAABGmioWAAAgAElEQVR4Xu1dB3ic1ZU905t6lyxb7nLH3djYYNNDLwZCTUjbkEZ6vmST3WwKISQbCAkJSQgBwoZqAzbNFIMbBhvcm1xk9a6RNJKmamb23H80liyPrJmRRh458/IlVqS/3nf++2459z6VnwOJkZDAICSgSoBoENJLnKpIIAGiBBAGLYEEiAYtwsQFEiBKYGDQEkiAaNAiTFwgAaIEBgYtgQSIBi3CxAWGBURbK1vR4AT8Xe6AxCUypQI0egMKzWrMyU9OzMQIlkDMQfRJjQ2/3doMtc4In9cTiCuoVPD5/NCZM1CkacQvLhk3gkWYePSYgshLjfPTt4/Bk5yLNK0bXV4f1GoV1FRDJXXtaO1w4vPzMnBVcXZiJkawBGIKoj9srcAemwkT0jXQqAkdLmFq/s/BWhsaW+y4c3YqbpyRN4LFl3j0mEasy60O/M+mWkwdmw91lwuSoRMQHaIGamjpxOfmZ+HaKVmJWTgLJBATTeTs8uKra44gMzsXeWYFqwqA9tM+Eg1019x03Dg99ywQX+IVYqaJXj1Qj7XlXZhXlAGXx60Y0fsUADnw+QWZuLo4oYHOJvgNuSZ677gVj+5yQadVw6gNePN+aiKrtQV3zU7DDQkNdDbhJ+BtDzUVZE99OzZWU/s4OyHemQyN3oTpmRpcND7jrBNg4oWiBFGLvQvtHj/8vq5TZGjQamDWqxU7qGf44e7ywe72Kpop1FCpNMgyy7maxLyMMAlErImONtvx2w8bUN/qhNfNMPRQDFrdeqMZ312ag3MLU4fiiolrDKMEIgbR6gONWHXMh4npKug0avgGya7VMPgoGqqkrhPfXpyBJaPThvH1E7caCglEDKI1hxrxzAEHLpiYOiQg0hJENmcXNh5uwnfOy06AaChmdZivER2IDjqwdFwy9CE0UW9LKJx3EU0kINpy1IpvhwDRO8eseO24C/aOtpMup9bokWnS4JtLCmhL6cK5VeKYGEkgahCdPz75FE2koW0jQcVIRhBEG0qaQ4Lo6V21eKvGgAxjl3Lt4OopObhmOxkAaQ4CqTCSWyaOHWIJRA2iC8annKSJZFn6uKwZVqcPRrMl7McUzDEWCZdXg3tmabGsKP2kc/+1uxZvlPtwyaQUJf8mNpicI+BbX9qByRYnvresKOz7JQ4ceglEDaLlBJGBAUVvt2qQpe3dw83wODqwYEz4HpZCLRLvTK/Dp3jNcemmU0D0epkPy8cnKcDpDaKN5XZMTXbTqxsz9JJJXDFsCUQNohXdIAp6Z+Kpba50YIzejh8tHxv2Awx04Or99XjpmBfLx1kUEAVrLUXzbSh34Jw0N76+ePRAlxnw7530EOvsfqZoujApwzjg8UN1QJvLiya3GqOYYzRqIrQFwnyI40yGy8c+MVNJZA75iBpEF00IaKIeEGmwsbwTeVo7fnrR4EhmbxxpQoPDD4/bjf31dtQ4VLh8Sja0FLLk4ZTljKBdRzvK4HNi0egAM1I0mk6nxcVj01CQou9XWDYCZtW+hoAW7dake+vsqGj3M/blwtLxqcig0S4BU7nPdWQbpJuYwxlgvHywEa1uP7o8AfJdcOiNJszK0mJ2Xoryq/oON1470kKSnhc7ajrQ4DKgKMmDqTkW6PhyK2fkwqIEbKMbz++rZzCYr+btUkyFNw42o4vB3kunZsEkN1CpYaAsbz0nD9ohwG3UILp44qkg2lA2NCD64suH4DbmQeV1wO1yQg8XVhTnn7ScqWkfbTxcjzYybo0MVAqyRGAerxrfmm/GwlGBCes7DjfZ8Zfttah1W2CgU+f3+RSyXH6qDmNStKCscajJzdiVD1pG3x1OD/TqLlw4xojPzs0/7aze8uw+GFPymUviQ/WKn/l1KViebcPdcwvwl49r8VGNG36tER5PF8ak62DReHGgwQW9wYhOuwtmnR+XjzPg07NOf7/eD9PY4cL9W2phtbvRxhhwWmoq3ATzuNwUajkmwKtb0OLW0BnSEENqOJlxKE524Y5ZOZiYNTgNFTWILg0BoveGCERfWVMCY3I6Y0ZJZAEEUiuhWgaI5gkOLTVGc6cb71Ab/OfyfMwrOBVE/9xVhxf3tkBDcJw7NhVFmRYFQDKELCcenwwv0Sj3k2tWWe0obetCLf+9uthCIPQ/sXc8vx9j8nJ4bwsnSbzJwPK77kg7rhirUUD+wgHacaOSMSvXqNxHPga5q5dglvtVWDtR2upFbXM7bp2Vjltm5gyojmqImv/eUAMHjCjgx2BWeTAlJ1nRtHJ9ea3gO8nFdPxdSWMHdlbaFG34uQVZuGYQ7NKIQfQKg43PMU50+eRU6DkZweVMz6Xt3eOdGK0bvE0kIDKlpGPpmGSCyKsIMVRkXCa+B0R0+QmidfsbTgGRg5ngF/bUYfWBDkzINWNajhkpJj21jk+YTnyPAOuyd/Bdcn1yT/mb3OcDshOOstrgmmKzsgyY+Pu+Q0BURBDNLxQQebsnD3h5VxW8XR44nV7MGs+/F6URvALUAMshwHMIOA3Ks/A3m4614HhjJ0GUiptm5nHiQ2Op2ubGf68vQ4fPiKVFJozJTGae0kuNHHg3sSPlv/J+fF3l94GPBmhzeLCHmYIK3uezc9Nw/bToOF6DApEkW3uD6PWDTfAwe39eUeilpK8YRIBarQ7JXFZunJHD9TkAinsIIgtBtKwoGU7aL/2BSL70IIy0XNybaWu8GQJEZeQx3ftqGSZTO53LCZTJCwg5ECo41OxEB5cviXPJ12vmjE3NYmEBfw4yMoXa8mFZKw7XtOPBK4owPvNkL1Ke8SQQ8bmDdODNRxvQ4vRjSm4SZhQkKwASDajS0M5i4tkvzE+BUnd2WjSi2Nhbymw4XNGIR2+cjNFpp95P7nnf+2U40G7CkgIN8tLM3eANnC/XOdrYjmaX2ItqJGt8yjOIRpR7BWxMHzaWtqGs3oYvLqJGmjKw5us7j1GD6MrikzWRlkLeUFKPRjvjRKbw4kRK1Qe0aGuuwTO3zTzhnYhN5DHRBvJ120S0MS6ZSpptL+9MJv893q+F67/RbFaWDvnIXFz9+tpEWyrbcP87Fbj8nAIUcDJEu4k32e7g8lfSSBsmsGQGtZGofq3RghXjUpBiNiiAExC1M7L+2t46fIXCXjEu8xTVcDs10bj8HCwQTdTNWBBgdinLow/JJh1qWx2wuvwoafbB1dlMzpUGHo0FM7I0mJqfAju9NaWciueJUf9BhQ0pcOK/Vow95X6HqUF+9UEDFo3NQF6ylvfkhyCFEATHZjonLV062GnTabrald87fAYkJyfB7HfgvPHpfCfaR/wPVzfFs+5sb8X9F49DhnlgJ6L3wwwKRAYdNZHAunsEFEn45r7JoMXO6nbsKavDP2+ZcQJEazmxdQ5qC5cLhxrsqHeqcf3MXAqVNkb3/eTnNfsbKSAnFoym5uuuZZN40+Xj0jAqtcc7+8JLB+HXJ+GSiWkK1UQ0jHyFHxxrxl5O0n2Xj8HMvJ7at8YOD37y7nGkp6UpS5NX0MnrGw0afFjRgaqGRjy1cnpoEBXk0KgPgEiGom15Lz015YYjzTjW6IJB7cLyyTkYk6RCKq37t2kGVNuBiyelsRLGx3cMXFreUWUyYfv+Cvzq0lM93l+9dxzepEzMzdWjg0uTyF8+ps18ryNVVqyYmo10oxq3z85XZCvR/xZqpXX76rBkaoGiFR0ErSgAj8eHVw624tapRmqjyKpvogbR1VNS6d30AVGEXqmR7viO6o5TQNR7dlYxTvRKqRdXTU7uAZF8qfyy3jjaiRkpbnxjgDjR3asOIDMzGzOz9fS6aPDK18drbK5yo8jkxI8uGE0b52Qe0xOf1OC9WhWLCZIJBOFOASYCcMsAIBpPEC3q1kTKJ9Utkw/L2nCE4YobZqRhRVEqlyfDSSD8/dYqVDi0uHBCGie2uz5PCa7SRS9pxY2T9LiyuGepKW3qxC+31OGyGQXQ+r2B0IfiGND+222lN6nFlxaMOgXo8ovrntyNaWNzsYg2pyyrsrTpCLLdtQ6UVDfg4asmIzOCfGTUILp2ahr0tB16G7wSAAwsOSGf/ZRfmgmibVXt2Flae5Im6n3g/zHtsY5pj2umMO0ha3gw7cGfXyvpwKQkN743QMRabKwGh47R9M4TilKt1iAtxYgfLslDcfapLu5ftlXjoyY1PbJuEPGdTHzezeXtqG5swpM3TgupiSYQROfSq3R0e5ViKFcy2Pfm3gbcPDsDd9Ao72984eUSLJxUwOIGagap0ZMlmv+uOWzHJYV+llj1eIY/f68MtV0WXDnJwiU8QPaTJbqkzobtZJbeOcOMq0NoFGGb/m5LBT6qcuGq6ZlIs+gVz83I5zza5MA7e6rw2M3TkJvUf5yt7/MPAkTpMPYCkajSFnpHTno14laGMyRYWUKr72hNI/558/SQEdsgiK6dmnpyxJogWquAyDUgiMpoOImpoVH5kKQPrPdVNMKt9JbG0pZw8JnlG67n8z+1s0H5ezvjLgYuJbfNL5QFJrCcdYOoqrGxXxBNVEBEh0Bx8QPLmbj4kyxufOc0OT7ROLc+uxfFhblYQsfEQY0pQzTE/noHdnDJf/BTk+jCBzTYL2hQV7lMioYOelwmvttqeoIVVW1IoqtvDMESFS0sYQdrmwezx2diyYRMePj+AqJ91JQb91fiuTvO6WanhjOLUdBjFRf/kBM3TEvjctajicTdf3FHJWpp7Gm5zIU7tAywGRnMe3zl1P5BVOGj+9kDokDEmjbRwQ5MtBBEy8LLnYmr/yxdfTFxDtR3oLyNEequnjiUgfbJtMJAAriLLrlZ7ceMUUKSkwUtoIk2lrWjkjZRf5po0qgcLOEyIZpIARHvteqADZeOVuOO2f1rIdEQtz+3DzOK8rCwsFuT8XdiMpQxRvXqjmr84bqJGJcR0Jq/3liOY3YjrpuawiUpoIlkJTja0IFaxo30RgOXt9Dz4BcBeN20iVKVJVq0uxjyNn5U60qacNVEC25i1DzcEZ0mEhBNT1PQ2+PiaziprTD5OvGl+QXh3l+JnmpVfozNMNGoPHUomogguqEXiOQoMVZfiQBEj31cjfXldKXVDMYZdRiVrEFxuha0J094ZfLVF6ZZlGvLrIhX1eakJdo9BEQbwgDReb1BxOusJojO50r0uXn9y6U3iBYFQcT7ysdZSkryGzsr8cfri1HEBHWLowu/3lQJr96CC8nr8hBEMgRIEnaRYGIA9qcfsgwG509MkGR+RG8cs6OjtQF/uqZ4oNNP/D0qED1PEN3YDaJgFl8efs3hDuSoO/BfF57qSYT9RH0ODIJoZTeIgjaRTPTLhxg8NA+sif72cQ1eP2LHuGwLpmXrUJTBSDXjI/LMIjyJ28h6JvHDI00uHGcuRcXmE2aNH/PGpAcMax5i5nIhICqvoyZaGdomKi7MgYBIDHixc2WZWn3QhmVUQuGAaCY1UW8QyTMeI4he7wWiTeWtePgjK1bOzGTQVFI1fT3k6KRt1GoJog54OlpoXE8K+yJRg2glvQzRRL1B9EpJOzJVnfifQSZgez99EEQ3TQ8sZz0gUuOlg+0Dguj1w434+y47o9T0fCZlKgKXL1C+cLHhdlXblMSrnlpGw8BnR0sDLFymWzqZy2Li9DMLCxUQyTwJiN4/PjCIljJI2htEspxFAqLFY5KU82UoIGK+77VeIGpn+ODXGyvh0Jhx2YSAJgout+sZOzvS5IQlKfJ2PbIquJl7nJ/hItEvfGZE1CC6eeapy9nLh9qRAYKIAauhGgKit7ic3Tyjr2Gtpq1xehA1ECQ/eec4CrKzcH6RWUkHiNIxip1BF/m1A1Y47eSLT05TKLZqvZHZdh3msl/SX7ZVYVuzFjdPSz5hWMty9h5BVNafJnpuP6aMzlEi7SdsIt7vmb02XEab6PYBbKLbaBPNHpuHxSd5dwEQraW9GVzORLZiEx13GLFyWsqJ5Uyeb82BZtQ0WXHp5FODob3nxMC4lU4JCfSK6xFEejof10WY/ogaRJ+eRRDxoSVsHvxiVlFtDzWIHv+kGpsbdLhtuiQU5U6B+0my8oX9ttNqohIK/wfrKnHznBx6NSZ6jkxF8FxhSL560KoUWN7L8MCEEPwhcfG3N2twCzVgYDmTdIiW+UEbjtf2s5wRRFPH5OIC0UTdCVh51rUlNuTrHORZnf7juuVfezCDDTCWj2Xkmucr2oWaqIwhglU7avHQ1WMxvtuw/oW4+F4zVjL04e62iQRErxxuh6qzBb+98vTLkYPajGGhnsZjCpwYayJ33efzUCah0yyhlEPUILr1nCCIAuuxMBtXUxPlqDvx4xVjh0oRYS8rah/6sAlzSZudnm2kwIIgUuH5/e2YQhe/P9V7hLbEt185jJULixSDVM6VWEoNUw/Pc1IevHIcJyW0sP70YSW2NWlJlUiDj4a/zKhM0rvMMw0IIoJANJEAT5ajSjaxeHFXI65gzOk/FoQ2rt8rbcY/9tjwqeJMpjAY01J4U4pDjnfLmP4hMH68fOwJXtN9G+jiu024iaEPT/eHLAb1YeYBt1e04ZuLMjEjJynkPFS2uvBTZv1tbsahPD2OgzKPpmSMMTvwwGUTwp7DqEF0O0EkQpVAlXJz2kfP77NC4+rE7XPDdw/lXCVRSQGMTzWGJH99hbm05PQMXFucdsJWEMP6qZ3NyNF5cP9lob/wIIhuWRQAkYvxECX4x0l97pM63LM4F5+indR3iOH64OZa5POclbNyu8lrtIn4vm8fJ4gY13oilGFNTTSNmmhFtyY58W58v43HW0m9sOOyyUm4iH+f3IvDs7+hE3/bXgdTajqunkB7qDtQqQQbee6/djbhMzMt1FA9ZehVbS5849WjuGhaPsluPcHNJLrs261q2Buq8QOCLtT4x/Zq1KjSMSvdq8T1ZEjMTmypDYdq8esrJmAqnZBwR+QgIl/n+RInYx4ng8jAL/z/Pq5EJR9Ebzo5pD/QwyhLDO2Rexem4LwQxYtffqUEuVmZuIK1bu1ujxIKEBB9WNaCzUfbyJ3RI9tCKgCFbqSbet2kdCWtIAS0771RjpVzcpX4iqs7CiyG6Kp9LCpoteGByycyIdqFpk4PDjHGJSmvjcxxFeZnKWEMIXEFPxQB0VtHW3GoqgH3XzqRRDYDNXCPTXE7QTS96GQQyScmxxh4nTcPNWB3DcMMXZ1YQvalDNFWGw5bMXE0+zVNywxQNgKKT3HVYdBj3Y4y3Hfp+FPE+BsGHFWpWVg+yoC27lSJyEWKQZ9l2mY8ZZBsUJEvNIpBVjX+yiW6lYzRnbVtuGPhWGSbSYdhykQWMlk2d9d1YO3OCjx58wykKczO8EbUILprzskgktt18EXcNFx6k8UGegwJkLUy7rGWRu43F2eFBNHnVh1CKjXRyqkBu6j3pG4qbcIhKyOuFLaHf7SRchHM4svX+v03jyLZYsFtBNIJV51g2FXdig1HmxXmorj4UseWk82CTArT4GUcjIw/C49r5d+DtCUB0av767CrjJOek8aJURGcBqZNTChMMeCHbx3DDGqii8g/761NxKDvIlgyjHpUtdmxiXaVU2VQvE25d7LajSunZSnBwqC7rmTjKbzXSh1I8bbjhxcUnSJKcf3v21KveJ0TadcpdpQEKKlVbPww1vFciXy3tjYr56akpDEuxxiZ2UM+WDY6yWaQdxMFICyDJ/Z0YFFWFz7LeFYktNmoQfSZECASIQQANHCgKygRHaOqTaSEPr6tDt9anM0Yy6ll1MJdfnxbI4pJeb2OX6tcXWyGgEYKhCgNvE5NhwNPfFRLAzYf87uZjU/vrME71Sp8gaQr+bId3Xkm0Q6OLr+SABaKrAhxDhmHWWYh6fvxcVULI79urJgsvZQCcSIB1asHG7Cn0or5ozJQx2y/nrQXjc4AZ3szPb52LGAa4XImSju7I9ayJK2mhyn01c8uHM3lmsdKlLwXoU4kJuBR+EuKBgrwpNYywey2WfFLastQJDh57wc2VWB3C5OzE3TUyAHwysckGkn4WQLeHbSg5fpzC8wwCVD5uyBYRQNVtnZie4Of/aPa8JNl+fwwwjeq5RmiBpE07DQxruJV1GH0Iwiif9Am6A9EcvXV1ABP7mjD5HwLiew5SiDPyWUpSEvTE0S1bCT65LYa/OLiUYwLJXF5suOZ3Y3Y29iFiQwyLmH2PC/J1K3Clf5ttOuEUxOAvSwjzZ1OLnVNnHQ/38+Dby0bB7cvEIex6HR4jcvZYS5njzCi28Y0QQlDBUcbnagmM35HhRWLJmXhiim56OBkKsFGmhyPbD5G7rQKuSSy3TYnGylsvezuNoaD2lHAJj8buezJc7zIQoIjzJl9d2k2GYv99ydoYA7wv9eXo9VrZBhDtKKF9BKyFQjUgGEumoZLE39wSTyp1/edTNpMqbUdL+xr5YN6cdE4Ixuxhs78n26GIwbRi2QOCjXjrlkWTgBB1CtaGg2UJNUg9shTn9SfFkRy7Veokf5OjTQ6Lx1zcjSYzuqJoLcm3mFtuwtPbq1UJop8M+wieHQ6PZONLexiYofk6a6cnkHuUIpiH4kal39lSO7ITiPzRaZSrM0NpGxkYx0Bs3xynsJylONEE71ZamPCuAFP9MniN9s9uIcOwNxxebiMvKWgJpJJ+9v2eowyeVFBr8iSmkmPKoVg4bIs3hufQUO+iEy6vMN+ZuF3NnhRWdeCzy/MxrXkBA00mknO/xm9reMEc05mEikvWvKgUk9oG3luGXbRwsK75ruKJv+I9tkhnqNmQcTPLhh1Cj1loPsG/x4xiLZUMOS+zQoTq1ylJCWSpSv0Q8kXSHXu1+Ge2XosC7Gc9T7v5YP1eL3UyfyRH0nkSUucSohqHredxCqyCBxeBhdTkZnGEiNXK2bnG7CMRqx4Zn9mALHMYeFkyfJFumqWni6xW/kQNAz5d7a3IY+lRl+am40ZpJHe8fwBumSk7bLaJFAowM9ZQ4J9Zz2evilE2oOG9SwBERmRAqJg2uOv2xsxmxMrPKOXDrWinAlVof+66CTMIGFfiGMfVDgUclgHAZFuUuGKCZJcDd/Llbq5T5iFf35vM6rIPEtPT2Fy2avYXUvHmBTjfgOLPV2s8hDGpJdzZ1K5kUyD+1vn5jNnGNkS1ntOIgaRnCxAqu7kGt4nxhAucvseJ3aUllptMZeqINXhdNeSNf9l2iZiZEsZlcRJtrLmrdWj5URokarpwgpWzC4oTGHMpYcX4+QJa3ieKE+prthcbmPGPSUQudXokKr30+Xv6Sf5FhmCUpLk7VVHpuFzpvGSl9D26TvEOzuHIJJKXlnOgsvk7zeUklaSiqlM+F48wcIeAi50dFEb8LobyaNuYorlhunUOCIHmnhCmO/l9EUs1lfZYaWDYCFSFBmt2tvIe3lxPZ0F4Y8LU07D2FckmfohXc4ifqNhOOGFvU34mLVcsjzMlBzZODIH0weuYpUcVPIQdmYTEM0REE1I5SQGQhGyWD5M41eWrxTWx6kI1vNHa+kgBMDawWewc4JzSA6L1ZBlnkop6uVqoOeKShMNdNHh+vue2na8dKAVTkMmdE4rrpjMag5qljM1BERzx3eDSOJZUohAYD/6iRXL8tVKTu5Z1r35TRlI9bbQQcjApEEWDp6pdx30chYPD76VBPuXDrJnkSEFRQY7udBpKOzTDGK4nzMAony629REvaggf95hxfl5fnyGFbAS21m9vwXNqjRoHFbWlKXRbos84z7c73bWLWfr2fjq9aMOhWC2KFeFq6ZkxEXDUAHRPILoKkbWBUTBEqRHqInOy/Wf4BO1Mbi6aj+DpB1kH9IhuKY4ibV64XdSiScAybOMuOXsHUaZ1x52KLm2C4v0uJpNCuJlCIjmT8jHtZNSlYhx0Dv7I0G0JKcHRPK8Yiut3teID+v4s0foxsmnjQfFyzuGeo4RBaJNzJW9XBJok3L5eCND96fnzAy34AVEiycXMA6UBptDqjUCAcwH2G13cR8QBZ/tVXbsWF/hBkOMuHm6eJQjTyONGBDt5LYOz+xtZ1Zbx5oqFa6MsMBuOAB1G0E0riAX8xmbcirLWaCy4q0yD5bldvVLj5U2Nx826qBn0O9OsiOmhChhGo7nj/YeIwJENQzW/HFrLTz6ZCzO9QZiKnE4vrLmMBqY3nA7Wc7aa0hg8dqJeraKCV3tIbmsZ1mqtLedWQBPC766OC/AShghI+5BJLSGP39YiyZVBiYY2vCFheH37BnuOZDUh8K+7Fu9ybyehZkHy2liUhIIffSDGtST51OkbcXdC/KVRlQjYcQ9iF5k5eh2qwkpPhvuYS4pI4ZBuTM9YZUssvzrjmbSRMy4aJSPbID4svn6k09cg2gfCwwf+7hZoXt8fl4m2XaD6+h1pkESzv0/YgeT5w50QocufG1hHiPvsYtkh/M84RwTtyCS0uY/bKlBM1KxOMuJ6+LUDgpHyJEe8wRb8h2yM4jKZe2eJZFTMyK932CPj1sQvcMO++sq2XqFJUhfOzePdM3IeuYMVjBn8vx6cpMeon3kUhlx63QTFvTTf/JMPmPve8cliKzcCuu3G6vYg1DPui8zFg9ADxlqYQrXRgxkoU+E15piqJ8AeJsf0dtVaqWi+GvcekIKReN1xCWIXjvUhA11WmT5bfjO8tEKYSyWQ0ArJP2Gzi5YSZBrZlpCuqtmcP+1LLramfx3EimjRRHSRgfzzLKc/++GKli97CLLD2lhYfzm1+IORDb2gPkdtZDNb8Tt7LEzj928YjUqW90kg7XhILuXdcKs0FOl5yTYEF3hPVMbmZMzAk0nXDZGk824lHmx4drYbxN7RK4p9SNLZcO9y0bHrTaKOxBtKW8j/daHXA1tofMKGSuJFYRY3iz8685UeG21mJVnQi6LBnOoefLZ4ElaujS0sxk7a8J21Dhg17AQkKAab7LjcwsLhiWG084P6uEPatHM/tN3zUzC7Bh+UIORclyBSHJij35Yg0qkoTMAAA0dSURBVHKXhf18/GQBnrxZzGBeNNS5b7Dey+1TYUG++bSMyjqCSYoPN5FeKk0ezstjl/0ZWQpfKNbjFWb7t1rNmG5px50RFoXG+tmC148rENWwTuw3rDzVsHzn+8sLkRNBy7doBCbLVST1VU/vYM1ZC4sTnB24m3GrWaw8jfUoszrxEEMdohm/f35BRL0UY/1scQmiN7hXx7tVwJRkD9Mb/XcVGy7h9L1Prc2Fh7fWwWckkSzVhVtnR97zOdJnF8rI72hg17r1rOzVseggtto50ueT4+NKEz38QTWqPclYOZFLDAsJ423IhD72UQ1KXaxfU7fiy6ySGA7Xex23AFtfq8Nksx2fXxB/H1fcgEiJDW2oYHEOt+RcnE9SeXyG+1860ITtLclI72rEPecWIMkQ+/jNYXZ1fWRbEzJ0PnyX7ZIHswNRLD7MuAHRztoOPLWbfXyMXnx96ah+y4ZjIYRIrvkyQbStjTv3oAlfpJc2hMUi/T5GG2vpHtpcpWyD9eWFOSFbJkfyDkN9bNyASDylzc2s3jS34tPnxN7WiFaQz+5uwD5nGibrWnDXMHpLj7PM/AiX0U8VunB+d0eRaN9hqM+LGxA9vbOejQl0uKxIFXPXPlohSseTP9Jua/CnYVmOi+zK4aNqrOXmOx80W7A4sxPXxBGvPG4Ma5kcIZ4da/Fwy6QMdq+IP6NahHWQPaIf22mD1udmowd2vo9xCKI32LewWnfVITvYSgB3z88dlhhVuB9bXGgiqUT9zftMdTBC+52lBWFVr4b7gkN1nESPBeiNviRckNeFq4ZZG0iHkz8xvFDIjW++fl7+KXuRDNV7RnOduABRs92L+96rUOrP/3PFaKTGGe2jkUnZZ/c0o9yuwwI2gbqe3eaHw6DuPaHV7Cjyv5uqYWEe6LvLRsWVjOICRI3ssfPz9VVKs4GfXza2310Go/lKoj3HxSW2nHRVadkn21Pp2A5w6RgDu6D13yso2nuFc57wt++ntpZGYt+nm58eQTu8cK4/mGPiAkSSm/rl+zXIMqnx44vGDKojRjTC2MhseVmLm9whZvEJnjaXT2mIKRoyk5N13lgLpnOn6Az2ODxTw8YN+375XpWyGcyPqK2FohIvIy5AVNrswENbG5HDvjw/vLAw5vyhvsJ/ZGsNqn1Z3KSPpT5KJ9sAdUD+/8wMPxtGJWE86/xlKTlTQ0hyP3mrXAH3j5hXTICoz0xUcb1/YHMdaRga/HD5qGEHUQWXLWUfebYOlPJnB3eNkS3Na/jL40yACkHNwq60xdx07xI2a8hnk8/hHp18np+vr6AmgiKjBIj6zEBjpxc/e7cCGVw6fnLx6BMbCg/3RIW6n3Qg280dmzez42uTP1nZRenS8WYuccNrG0la6FfvVyr7n31vWSHSI9ynNZayjIvlTHo2/pKGNbeExS8uHxcRPSOWwul9bSkufIM9IzfVyFaeXvbUNnJP2Z7m5LF+jno6Hw9sqGbbY3pn5xeyP3Xsc3bhvlNcgEi+sgdIiZXeiT9eMYbu65mzPQYSnBJZb6WB7bTh6+fmYkwYHdkGumY4fz9Ou/FB8ooKuJR+g8R9M3stxsuICxDJV/57xkCqbdwUmHuyTozj7mESM3pwcw37ArArW3YXbmSX2eEYH3Ov3H/ubkVxpgb/sahg2D3Y071jXIBIOmf8nQnGfeyMfyt3E1okW5TH8XiS7ZL32fTcUakd32M1ijQdj/VYxwT1+lqNshfZTTPjK0EdFyCSCVjNPe63kUt8PhObVxQPn60RzeS/fcSKN8u8MPnt+BbTNJFs/x3N/eSc51hUsMeeiotyOrnteXyxG+MGRFIe81qFBpNNndzQJP7Ye70nfzMrUl467ILR78C9tE9ykmIb+JPo+SNbqlFpV+Mz56Swx2Psud2RgD1uQCSEdOEvm7V+fJs1Vhlx5ML2FaiUeL9Zxk1p6O7/4ALxlGLrCEi3kIcoG7Z+x3eY8oinGJHIJm5AJF/b7zZUorHLgC/NSY7rbmFP7wh4aDmsjfsOQRRrP2lblQ0vHvFhrNGOrywOf6fvSLTJYI6NGxAp6/6eBnxi1WMpW9PFG/EqKGShhDzAoJ9Tn0pKiHdYKCFPiCHfosGlRWpcOin+7MW4ApHSj4g7CWXquvADxot6b0g3mC9lKM99gUBnH0/ouCfaVxflxqxLffCZW8iv/vX7FXD61Pj2knzGpc5cErg/OcYViOzMWf2WSxo3b8QX58tuQLFhOEpcSnpJ50ZoEEv/bGl/rNWbcFEhO9gOQyezzdxK9OUjHhQaXUpZeSTFlkP58cR9nKj3A64hl3grucQzLW3ccio2XpqkWf7xSQMKWHu/mNs4jM88/T4gUm2xsbwF7x5jBzNu9DIjxYlPs3BRdjiM5ZDM/aNkGFR2peCyQg83vYkv1z747nGlieShSrmb8p+4pxmrhvENphXyuXXUUA+h4T7ECLk7JQ+OphqMTtFhAoEk98o06ZS2wa3M5jcTbNI5pJRbP3m4f4jH3oIlhUZcw81dhmOpDXK6TfBw6/WCuO0oG3cgEsA8vr0Ghx0pmJdmx03cXmmohzQo38NNc/fU2bGfuxt6tdy7jfX/yp5m3Z1fVdzOSdqAqMgtctlt7MhhYSTdouyDNlzjT6wsKWdF8IIMJ1bGWZS6twziEkTHrQ78/oN6NjFQ41622isgOT1Wo56synI2kqjjdk4dZDSK9xXcCFmaXI1JM2JUsgGjYvgMod5tf307HvukRWlu8V02cui9b1usZBHtdeMSRPIy/9heiyNubuWktyo9nf+dhrAX/8aNlWu8adTGndRCw5PkjVbGcQsi0UZ/YfthN13bu+ekYmauJdp3HHHnSS+kNaVdSGJa5Wvsrh9vEeq+Ao1bEMmDvnKgER80Mlvub+dWBflsnhDb9EI8oK2R26RLdzS7yoQbJuu4hdXwMiijkUFcg0i8qD9SoG3qVJyT0hkzlz8awcXiHOkU91d2iqvoSscYbQvuWRz/PaxFDnENInlAcXOf3GWD26/CdcXc+z0OmzwNFaBeJf1WuuYaPdS8JOcNZ5n2YN4h7kEkL/d+qRVrjriZxe7C3azVLz4Lt2f4iF1sn9tvo2eoxp2zSPeI034EocA2IkAkDy7c5r02C7/SVnxhfnbMc1aD+TIjPVe07dN7qG01JlyQz6TulPjZTTKcdxkxIJLm4E+RglHmTkWyl1s5zck8I/Vf4Qg1kmNkY+End7bApUvBjKRO3D4vL+bUkkieL5xjRwyI5GXE0JZmT/VkN1vczbhzduawdrkPR6CRHHOQrIXn9rfBoU3FRGOgxfBw9ICM5BnDOXZEgUheSFzgZ/Y2opaBOKO7BTfPSMXUnOFLRYQj1HCO+biqjTtSt7MTbSomWaiBmNA1xTihG85zRXPMiAORvGSL3c1WL00oc6VA42rDlSNoS3Af3fh3jrXiraN2qEgpOSfdg+unZ512V8ZoJnY4zxmRIBIBSXe1F6mRPmnkVhzeLizM0ygsw1jznQczOdIeZu0hK/aTWutmQ/UVRWQEcB+32BJKBvPE4Z07YkEUfL33S1vw5lFu6sIG5en+Vm5zzsBkfmzIbOGJNPRRWyts1EA22HWZ0LmsuHJyElkBI2/78lBvN+JBJC8ljajWHmpBgzcZzvZWNlI3YvnYFBQOU4nz6cAlbXPWl7Zhv9UPrc6AsSYXrpmSxpaCpsFgMq7OPStAJBKV7h3vl7ZiQ1kH1BZmve1N3J/eqFTTjj4DYBLwbK1ox45aO3RJ2Yr2uXBCEpYwFzZSdpkOF6lnDYiCLyyND97ll7+vwQ1TajY8bXWYxyZVs/K56V2qKaZJXGlMUd7mwK4aO/bUOmBMzYWXYJ6TZyC1NS2uOUHhAuasXc5CvZhUjmyr4l5l1Z2wpLILmtOOPLOPOyhyj4xsC8amGYbEIxL+9bEWO45y64TDzW60+kxQazTwdrZg3iiyIQngCXHcoGIw4Amee9Zpor5COUbNtL2qgxPtVjaf05uS0dnSQC9OhbHpBozjf7PZjzqZpO4Udq1lX03oGa+RJqQqZf9FBjnZL7GLnFrZ2qqdP7e7PKjt7qJW2eaBw6tCUnoeOlrqkM9ub9O5Ad9cljoXEqj/DuOsB1FwEsVmKqEBfrTZhZIGO/d79UJnNLP8x6gkPe22ZqQQWNIG2aBR92zCQuBICz5WMxFINLV8GhgtaQwreOD1OBUNN5pgmZhtwqRMA4qzLMNC4o8ncP7bgKi30KX/obXTjRKyJ+tsHrSyBq2dv5NaNEXjCJNfa1DA5WMfRw0BIxpKWt2lGrVIMarZCUSrcL8nZli43bpmxEabhwKM/5YgCiU4CV5KiZC0+JWObe3ssClYolLiUtezzGVx6YvHAsKhAEO010iAKFrJJc47IYEEiBJgGLQEEiAatAgTF0iAKIGBQUsgAaJBizBxgQSIEhgYtAQSIBq0CBMXSIAogYFBSyABokGLMHGBBIgSGBi0BP4f/YrzpyASUGQAAAAASUVORK5CYII=[/img]La pyramide régulière est de hauteur h et sa base est un carré inscrit dans un cercle de rayon r.[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAASkAAAAYCAYAAACmyAs+AAAgAElEQVR4Xu1cB1yXZde+2HtPAVkylaEgIq7U3CO3uVep5cjU0kx9NXOUuTVXZTlzo6VWbkVxQYoIyN5L9l5/4LvuB0GG9vWN932zl9uf+vs9POM8577PdV/nOudBrpoDzeMv44Hs4nIoKSpAS1nhL2NTsyHNHvh3ekCuGaT+ne5v+Owlv0UjIqME1fwz0tUIw9oYQ01R/q9jYLMlzR74N3jg/wRS/ol5aNdCqzmQ/h8m7mZcNnbez4SKihLM1aoxvX0LWOqpQUHu/+Hmzbdo9sBr7AG5SlKpS1FZuJ+QD1UlsWu/OirET3g+qvhXJIl3YnIx2sMUY91NoCjXHE3/23WQX1aJhRcikVEgQ29HPcz2Nv/f3qr5umYP/O08IJdfKqueeioMWhrqqJBVoaKy6qUvKTBIgf8oKylAW1UJSVkFqK6SYbSbCYa0NmrAptIKy3HoURpKyishL18DXuLe7maacDbSgIWOKjT/QHPJKCrHD7+noqyiCnaG6uhmpQszHZXXwvl/1vb6PorLLUVSWiGU6JOOrfQgRz+rKMhjQltTmGopvxbvXd/IIs57Yl4pxNQrycvDRl/tD98hJqtYWifWZI7No9kDjT0gl0eQmvVzJEx1NJGaWwCNl4CHgBkBUGn5pTDU1oCNsRZiMgrR1kgRszu2bOLV3feTcCEsF9Ym2gw4cjP+I8+/+cVlyC4ogbmuCpZ3t4Kx5ssDcPPtBPgnlqC0tBxOpmqYQrbWxljztZi9Lf6J8E8oRsl/Y3t9HykrykGdfq8iOy0WwC4nj6jUPAxw0sEMrxpWFZtdgpIKGVrqqkNL5a8rqp8Ne4afn+agoKxKAp4KWSXGuBlipIvJS+fvVEg6fgzKhIyb2PudzNDXzuC1mOdmI/91HpBAau65KDDjQBdLdbzvXQs6L4p+AqB+iXiGYyF50FZTRlJmATTVVeBjoYb3O1g0sXb7nUQEZ1agTxszPE7KRmxGEZQpANsR3Mx11RCSlo/CgiJsGmhPxtAwTTz+JA1nn+bBRFsNVlrymOfT9P7/Ovf8z56UnFeGBb9EwYBA7qyvhLkdX522NfZRXGZRHetUIEilZxXCw1ILq3rZ4GpsNrb5JUOBvjIno9w2yP5/Zti/6Oz4nBJ8yLXkbm3E+VNFfkk59DRUcCc6E31tNQhWppIleVxskZmF+Ck0C2kl1fBuZYRbkRlwMVTCwi6W/yJrmx/zunhAAqkPuLAqquUJUi8HndT8MqzzS0RxpQLU5SpQJKtGeZW8BFKzvJuCyNd3E/E4Q4YONvr45XEiRrQxkEDqeHAGLPS10d7KAOeDkzGyjS6GOhvX+epyTBY2/BoLRiusTNWxro8d9NUVm/gy9FkByiurJXYmI/2wIvAZqCvVnZdTIkNcdhGs9DWgr/bi+nCCZVG5DNb1jtceczDSlNS4cAEWIk0hILQhqNaOED6zlOmntZ56g2fV/jytoAxLLsYghWmblZkWvuxrB72X2F57fmMfDaePalms2B7ExiDYlUcLbXx1Mw7PSuXhbUu/PYzH/K7mcDXVqXu37GK+b24xFGl4FSuDSvy/vu3imdn0STx9YmuoCR0yMfE+wofKjd6zvrOziisQn1si3Vf42VZPA7pqL2dxMoqUG27GE3TkCK76OPsoAUV5JfB0MoW1oRYuhSRjXW9rMkE1zD9P/a24Erb0r4uZnmTDpbA0uBkR2H2aMvP6NlVV5OOX02dw2Pc8cvKLYOLshXcmTELXdjavS8z9E+2sRkDAHeSWa6NXJ5cmz7l6bCcuRihhxfLp+Gcl1unhfpj16S7MWPoF+no03nCq8e0XixBQ7IBNK6dD/U8WruVyCVIfno+CjCDVjUzKq6WWVAYf7VpDzxO5O67zS4K5oTai0vMwua0hwSYLBRV4JUjtIEiFZBKkrPVxKTQZR0a3lu4VSQD4+EI0hre3wr24HLTUkMMnb1hJPzvyOA2/ReYy5alJDcXQUOLPu1pIVa7acSgolTtwjqSNidOE1qVLIFr+hqXEMoQI/QlL+cnZpTDTVyVYtII2g/JcRAa+vZsGRYKlkaYSdr3lgF8jM7H7Tqp0Lx0Gn2gZK+J7CZAq533fZprSyUIHO+4lI4kvXEFwViHm9bHTxTj3GlYgxo+0/SJtJw7UFB+IMuovsb3+qnmVjxqvrFk/ReAZn+3SUhd2Rlq4+jQdhWUVBEpF7BjsgIzCMnx2LR7ZDHoVPlsAXBUBxUJbMDkL6n81PhHtDSk5ZdDXUkIL6lxJFOkreF55RSWGtdZv8D7ChkOPUnEtJh/M2qT5KON5lCIJNLYw026qD+aXyTDDNxxvthbsmb4oK0Ufe30cC3qG4Z7WuE7/e7VQZvpqgSEHHktsq5QbRg4lgB4OJrgZlYk2Bop/CFKFmSGYNmY0Hqfr4d2ZE7gJqCAu7A6+OfoL5q3dj8UTe+JPrvt/IlD8+25djVIM6uQM61G78fX8vk0M2T1/ENZdVkFI8Cn8s8STLR8OwsnINjh5dDX11BfEQRiTHX0VPXvNxPydpzGxv+ufnqs6kFJVUkImUzB5+RptpHbhvuv7FG3MDRgEjF5ZKVa8aYPpvhHcsbmzm7+cSYkADM2SoTN3fl/u/O95t6COokQmIsP+R6T+bcxxLfwZWqjLSfc7H56BQ0FZ8LYxRFJOMdILSiWAS6X4mpZbiJU9rCSgOsjAOR+ei8Fu5ghPz0ccBdcejsbIJZMITsrEKt5Lh4D17ulw+NgZ407UM2wfbAdjDWVsos4VkV2JrvZG3OXjcXxMG4iUS9j5Bo8d9o+GLlNMJ1NtmGipwEBTBReCU8iuqqCmokJGp0QWokEmVokbDDjBAke0MUFUZjEW/RqNLg6mUCUA3onNosivBjMyhqcpOVjUxeKlwnGtj7oy1Tn+IIbvpyqxTTEEGHay1kbvVgaYeiIU7W2N4WSiJYGo0KUiyQifJGZj7zBHLL8SS+DRQGtTLfwWli5dL97nVnQ2bHXl8Y8eNhBi/tyfo9DZ3hiXnySzSKIGY76jiZYq7HnfUw+TMLK1Due8ZmP64fcU3Eos5j11kESG9ozz4WGph4j0QhSWlOJzpqCNxXDf0HRciCqAD+fwUmgK9gx1lDaHz67GQiavjEouKi3FSizobImll2I4ZxVkpSoITi/GYHcLVopz4KSv8EqQEgG4ZFQXfB+ijwD/c2RkL/TMM7vnY/jcE7gfG4aWVWlIyQNcXe1Rw6GrEP7kMarUTeFsa4r4SK5dVR2UZsVyA65Ghzd8QDch4JYfsopKYWLnhLatGrK5zKRY/B4SBWU1PXTp1l66b2VZPh4/DoexrTPMDWpCviArBWHRGXBu5w41WTbCWDU3NVHHw4ehMLJzQbtWLZCVHIfAJ5GQU1WDV+cu0G2UKJQXZiGc6b247hGvM7Rrw+vMGgFONR7cuoVs2mvr1A72VobSez4JuIx3xo2BUY+PsHzWSHi5OzQAgn1LxnDD1cPVc2vwyC8QlRrMany8ofMKiTMzKRyBIQkwsnCER5sXrCiOPqx+7sMk+tCjY0cYqMkhMzEcu77ZB6dOozCqX/smNl/4cTcCEiswZfJUWHLdvRhkgLdvI6uwhP53pP8bMrA6kFJXUUZCei7sSL9rAjkJToYqyC5l6mCmDb/oZ1jSpSUDUBWzKbRXUzfxMlNjubxpuicCMIzB39PRCL+F1lTpxA4v/rZvqYcUVrPiMvOwkOyng7kOpp8Jh4OprgQ8clWVcDPVQFAaUxNjHbD6CC2FSmnxTj0ZhjFeVgjmKozPyEOPVrq4GVdIrUYB8Ym56NzaEB/RxvfIPjowWO7FZGLzgFYwIkgJm55my9CllSF+CkqU2N0eCvxBGeUYQtA7/yQFedzVVTlhAqg72hoSECpx5ekzSeCXyWRkj9WY6GODC9TNbLXlMZ8BN/NsONpaGqCQdt6KSMeMjma4HkPtTlONzEMJEWk52DrQjsyq4UqoYVIV6N+GgUP9SbAdMQRrKSQriUjLxdYB9th+NxlRWUVwtdCHi7kuTj9MhIp8NXRIa4SeF5NTjs52hrgbmwkL7lwmZIm/p5ZgsKsZTvLcSe2M0d/BEFPou/4uZghIyEVmfgncWqjjSXoRwVST6Rj9nZAtAapoMVl+JR4DXFpw7tLQ1VJTAt9fw7PhzjQ9JLVA2pzmNCqYiE0gJq8KXSl8n32UKL2z8Lvw8cP0cq4FY25YCdjC4ybPCyaiSDCD/hvoagH/mGzY6yngg1eke5lRN9DOtScWHn6ED4e7NgiAqopc+N16CKf2PriwZgK+vKKCB/cPQ4uMmNwYYzp5oMJrKU5vnYSNs8dh76UQGJqqQl7PG/t2fYr9qz6Ar38UNOjTvPw8dB0xH1tWzYQmp+z6ye2YvXw3VLQ0oSQrgbJJJ3x3aBtsFMLQ1rorZh30x+zBNanV4992otOInbid8BgOhX7o2GEmtNz0UZAjw9RFW9BVLw3TP/oMcipqqC4vQTGMsOXbfejn+SIosyLJNrrOqrkuuxyj567H0sk96963JCcai96fxfQ5g/qwIqpKSzFiwSYsmdILmz4dj1XbTkDdsBVGTFuILf94F/VX3aFV72LFDw/h4WyNtIxkpKVGQdd1KI7s3w57o4YJ4G+Hv8T8Nd9AXdMABZm5eHv5V1g59S0J9DbOGY+9F5/AgD6ElgeOn9yJuF93YibTPP0WZpArykC1QQfs+X4LWpuooZg2L6bN1yILYayjjPzMLIz4cAOWTOuD8oJ0LJs3C+cDYiX/5xfkocuwD7F55Xv86qLmtQlSFdXzz0dDjoHZzUqdu64MJdWK1CGAiGeFmOxtgx8D4tHTRhNvu5pKu/Li34RupABPGjmbKUXjIRiKAISh7mZkZyXUh0qgyV3VgdW+owEJqKyowPr+9lJ5/XhwGi7HFqGPkzGOPIhDKwN1qZ0hiizJ0kAL3RyMcfhuDNMMG6z1S0A7AoKWsiIXdRZZTjXBqhDe1rro7aAn6TgtKNR+cjmGO7oRbsdkYFO/VhLICJsicyvJMgxx6vcEHCJI7WUACaDoQwZxKjCRoNMC7mRS4tww2t+vtTH2+8dgZS9ruBL5V5K1yCnRyczr7HQVWGSwwNhjoVJAX3iSiqKSCrhbaLMIUYWYrBK83d6S4JeK+axauZPp1B/1feRPO6PJjhSYZ4pKqGgDyWUldU1/WwK2FnYKQCPo93AwwsnAeDIoJ4mlnA59huvReYjhPInhbqlLxlLFdL0YUzrb4PLTTLTiNjmvU0tMOBGGXk4muEwG29pQFZ92t0YE0+/Fv8RI517iuR4mSpIPAwkqPQhsB+/EwIEtIyqcD3GurZEOXM10mLqlcj5aQa+e3reDPougf7sRME8LMBpABku/i+PhOZXozvudpt93DHKo0+oyuZY+oNQwrG1LMr8stKJPXwVS/qfWotvYDbgUnED2/Opk5bvFo7HFTx3+t3+oA6mJb3RERfvFOLZxArbNG4SFh5JwP/Qm2nE93jm+Gp0n7UFgSjza6csj9MpRzFl/ATsP/wDD3Bvo2n0U5n97BTP6uUuAt3RcPwRqvoWTXw1Dd6dOmP7tdbw3sEbOCL60Bz3G7GEwBsC+5A7sW3ZBr1WH8M2y8ZCXZWGwpwPQ80uc3/wu71WBxVPHQtlzElbPeatuaeTE3ISb3Rt4k9d9K67jRin/fIMT12z4YDB+DLPEpYt7YUAQjntwCm+OWoQtp29jkIcuhnR0hO34b7Blbp8mcXlkzUyMX3YQ209cw5yR3sgKvwJPt94Yu+MK1k3vUXd+Zuwt+LR7E2M2n8fnU3vh9rHV6DJmO649jUB3Rx1s/XAwPjqUiPsh3DhMdJAedhk9+47BB7uvYOaAGj8tG9cfd5V74eL3y7Ft/gAcDGmJi7TZ8LnNvWjzzgsPYRH/DVyGbcGD5Hh4Gsgj7OoxzP7yPLb9sBsu3EjrQGoBdSLIKaCHtYakVxx+nI1x1A5kDJZ4AsyvZBn7RraWFqUAqU8uEqR4fjuC1JxXgFQUF+wApkMH78dBR1keQswmspGlGZBml3JBKuIdTzNsupWA+IIqDHNrgXvxWQTGYklrEs2h1gZqFLDlcZeM6LsRzlK1aCl3eTcyChHMQrlS572Dkshc+P+HnS2k/qv3yaS62RlR56gBKaPnICVsetPRUALKWpB6yuAXAXSMQLz7LUcpXRQAIs7tyeMnngeW0L123UuSjiuSwYjKoygajGc6NpgglUCBOT6rVAIoMXS5KziaaMA/NgfOhspY1LVGe6sd4hnR4hm058DdWEzzNIWWai33F7ocYMaUU6RVtfbU2r6VACDeSYzvmZr9ypK/EVNM6uBIZ3pWQa1nbEdLBCYWSIEv7JxIJtWFqaUfU+BtAx2kgoTQkYTmNbJdS9xgauJuoswZkkNAWinnwwz3OR/hz0QhQU6aDyvOh2CENyOfSXpYi3ralJjHxMJqgpsBfnzwwpc77yYR8CskwN93OxbLelryKwVtyXYBUvMIUqM8+fzILFgLQH0FkxIg1XMihd+gp+hm/wcg9cnb2EqQun3r+zqQmtTdRwKpoxvGY8PM3jiR0hb3fv5KsiHC/0d495gM7zFz8O7QgejUsxuzhRotxXfrLMzd+RCbN/wDChWlXPNKSH50AvM3PcGde3swb8AwTPr6t3ogtRe9xu3hRvAA9oW34dZ+BNb99BgjOpoycEuwaFRXfHO3HB8vWIBuXXzQ1cuxCZBkRV6DT+e3sfbsY4z0eaF7ihNlBTHo4ekFm2GfYRQ3nnKuNRUVSiazx8Ju7EEcXTcUQzrYwmrsbmwnMDQe+5eNwzLfUjx5cho6EsuswOTubVHeYQmOrp9Qd/qNI8sw+h9++D30OsyVSQWqi3HPLwDmrb3Q0lAN69/rg1NJbrh3boN0zdntczB7RyA20U+K9f20MZhp8jF8PKgrjPsvxWhmHrU2rySjdZ5yHF+Mkkdbz6HwfHs2/T+ogf9rDZKjNlC9gJqKYFKdLNQZLGaYdy4S7kzLRFUvg6nBO+1NJCYhRhkjQSxseaZY7savBqmYvBpAOHQvHgdGtUYuWcZBNmjGFVRiLBflXv9YjCOlTc4rZyWwHIPYR7Of57YkSKoRcETl6WF8Hsp5nQl7pOZ2NocZWdL+wBREEOQM1EgNmS5YsOLUi2xrt38cOjD9FGmhCEjBOq6SNewZ4ihVzXYSYCJJu3vRpsMPCFK0ac+DJOpUL47V7v4CFIT9tefWP57MQBToaPkcpARDEWB86WkGTDQUJcYoToghuCenFUCJWlx/FyP6tUWDhtfaZwgfHZHsca4rGDReXPXtEefuI2CLVO8YWegvkfnU/vRY1ChkBa4mVf6FqdlbBP2HSQWwYeDXgpTwySXqVt8MdZLsrKCPJxJkx3tZ4jpBwqOFCkV3IOhZ+fMNJh4tmD6KjaD+fJiaaEobgvgkqnacfJLOVolCDGLB5WhgEhazAikqjO+cfspNwEjq86oig57czrROz6oFqTHtW5KdZcFSu4b1vWwkBpyGc7dpOHwzAkPav6gI154bFvYQKoZWuLl1LjZfVyFI7ZPEYQEOU3p2RJnHojqQ8k1zx42zG55rVqzoPjiJJau34d6NcBSoqWPwsHewaf3HuLZpDqZvv4L2rtZSMUIMRSVWkk29sXJFf0zrORzTdl/CjAHO0s9CrnxDkNqNi2E1IOXeYSTW+P5OsKlpRamSZWLHphU4cPgGgiiDOLl7YNGqtRg/wKtOOxIg1anrGKw5zes6NWxhKc34HV1b90CZjduLyjFlFw0NTQyesAjvvd0OQ7ydYDlmF3YsGNjEjd9/OpYsUw23/Wp9Q8bdwwfF7vNxYsuUuvN9t8zEgsPpCLhzBqxlNBkCpM6muOH6Txsg4PzAimmYtfMavFxtXuqnGW/0R745SU5ttfu5zQPHLcDscW8gMuAkPqH/716v8f/AoVOxfvVHaMmsSgwJpBay8qNAkFKl1tHHXhe34vLxMDoXJswn37TVpUipKukz4lOYQgLD2bBsdp0rw+UPQCouv5IpnBEOEHg2P6f+JZWVFIKfYkpHKzxKZuWorAwT+EnN59cTMZRBdS4kDYMcdam3KOD3lCLcSyiAIYGpsrqSi74l1t1MpPguPr+twmqKt0IrmXrkCfq0NaPoKZOAQzQ/jjkagqk+VhSSMyA2RU8LTRz4PZ3ami7TQH3svxuHg89BKorA1dhOAQovs18cTy2qllicuaacFPwi3ZvkTfpNkDKmeOjN3qYyCt/HHmeQcSkglWnrm04GeJ+MU7VeT1jtM/o7m2CXH0V7MjXR1CktZvpZic+YxcXdmunWVjaIphRVoS9T4p08d5SLIZyMNbDNP1lKqW9E5aC6shwbqWFdZJXMl9XPcQz8M8HpFM8VJN1w/PFQvO1pQd2vkMEiQ2tjNakIcInp4jsdbeD7OBXaSlVSihZATWukewvsvR2DyR4mZHgKeCTmI7GQTFOJDLtSAilXglXtyCVTfo/60judbBDGPjhRQHAg8wonu1zYwx7HH6ZAjdriql62ddcIVi4qyxM7WOJKeBbMOX8fvgKkZAWJ6O3hDt23NsB347QGgVOW9gBOjp3x8ckAGN7fhBU/ySHo3vcQXLMa+Sy0MD3utxFH1o+VmNTpVDfc+GmjFGBxBJS4Ak107+CMjOREBAZcxXtjp2Eig65T2UlM2xCDuMhzaFzPLHsWiHaOvTHv6B3M7FvDiO6dWYc3xx/G3aTHsCuoAanVpwPJeixQLcvD9RsP4OzzJkzUKxEc+AgnqId99XMRgp/elPQ4MWpBavUpXkcf1x/lOWHwsm+P0TtuY+mYtk3Ao0qWjkE+7eEw8Vts+aBpdU+A1OYbKrh16wdoP9frJpNllnosxPFNk+vud/PoCoz49Coeht2EBZladXUaZgyfAp+ZmzGtn7PEpM4ku+L6zxslHx9fOxlzvs9EQuR5UKVqMGS5T+Fh5ynZvOwlNsfT/7HP/Z9J/wcEXMP746ZiwMoz+PrjwTUglSOYFBsQPVjijqSWIb7LU2aKVRNP7I+pFp/KvGjsFEAlOsYFKFhpi5JxU01qK4M5ncH8lospdvhFYXP/mvRElLzXs5cGCkroSyF1y41IfD/cGRuZKhTK5NCboHaaLQaiJ0foMp1t9KSy+hkee9fLFPsC0zGVacxTBloYBVwlOdZ8aM8YDwtcoJAoD5nUciDEbAFGNqy6nA7i5znsehY7oWg96M3n7rsbj4MjnbGLmlQSU83Gdr7KfnE8t1zoRkznlKol/WTdjXiks/zfm4zoInUdYbuoZLUmozFltfBMUAp6sWVhQtsWUj9Q7RD3SimswiSyyujsAgkwaocaU6qfQ54xTVRhIcAS23jug5RizO5szW8sswnwBSxGyCQNaxCFdxnpj39sLhdTFfvXRKqpSJAxx08EfTNNeQmkJpAxjWxrjlL6IoxFiVRqXuI5Q6gzJjJFvMOK0jRPE6bmiviEzHoQj5exDSM4pVBqMhXPGkKWFMiPykPZDb+UrSP2/GSpdoi53eAXj/g8GaZzE/Jjii560EYQ7PLIhk8+TMbg1gZSRbS2gVeA1PwLUZjVxRbnqa8ZEeRfBVLiOX6nNqL3yEVYuPUg3p84nCxaFbGRgVgyfSLu5bbGnbsnEHFiOXpM/xHn7txCv3ZGuPLjFvQf9zEmLT+O71aNwlfTe+FUqiv8zm2WQOremfXoOGwVjt8WYOLIql8YOrbzwoDlv2HxAEW4OvhgyJIDWLtkAjRkOfh65Tz8kmyDQ9tmYrQPBfNOK3Bq9zzI0sMxZ8JwHLvFEn92AGxyb8HNYxjWnA2SwKaKmtRwLyckmL2Lq2fXSVW9o19Oxay90QgIvCZtJjUgdRU+PqOw+kwQRrOQ0XBUYf28/mRnebhy+TTaO5gh+uGvmDF7GSavPIyJvS0x0NMW+oO34NBnbzcBsX1MhTcRpPz9D9SB1MRu3gSpj3CyHpPKTbyHTm27od9nJ7CeetmdY2vwxoRvcOVxIHo4G+DLGb3gS5C6eX6zBFKp1La8PXvjrcUHsO7T5376bB7OJ1jA99Dn2LNwEFacyMHlS6fh5Vhr83JMX3sSbSp+hlufT+i3QKaDwv9P4ePhhR4LTmDTvH41ICWY1JSToVIDngHTFRFg/90QQurVCFZ7KGwt5mJt3JsiPmu5m1hE7Ugb9ylwf82Uy4LAJoYIuJuxBdSM9CQdYpCzPtmTIf5xJY6ApCQtfNEYKCMwPknJF32d8LbQIkNitYqfUPiGZsODvUt5JZVIY2ncks2VOfwdTOVkBxPbmbBaqC2xiZ3+KazQGZDxKTKlLCOo5aGEZW83GwNWzvJxZGwbfBeQAr+4giZ2vsp+cfxBMr8zI9a0IRMR706QZ+UwCaHPSiQBX3SLi4BO4TODyCbcLXWwtu8L9lDrW3GvOwmFBFM9qepZfwj/ihYCNza0imck54peqFjkcGNwopCuw3aIgPgcDHJi0yS7tr0JyKLYcItlfDkCdy5TK0crPUnz8TBTl6qQ4vvMt6idHbqfCG1e704/qfL3VgnAyikuRWcrHRYCatKLIKape++nsvVCmY2vQuuqmY/HnA8h2Iv0v22jQoC4LvV5Q2shm6u8rfWkNDuWBYSI1HyMY5WxF/XI+k23AqRmMB30sNIn8BVI62lRt6brqb5vLp/6DsvWbkYONwtVeUWmoXJw6dILX3z+GVqxQlWWl4BFsyfi0NVEWFqZw52AE3PnAqz7rsSBL8bgKwbYKaYqfuc2SSBVXV2KvWsWYfuBC1BQY5tHWTXa9R6GDWs/hRGrpX5ndmHOku0oV1Tm+qRWKN8Syzesw7DubeB/fg+mzv0ccuqGMGvlxO9SgTO/xuO34NtkUgQpz+FYc+ZRHSNKDL6GadPncd3yPoqK1FtV8cnabRjZz7PuFSWQ6jQaq30fvQSk2J6SH48lc96D7614aLKNRGrC7jsRq5fPhjF74/LEatYAAANpSURBVL7/YjY+WncaPuPm4OjXS8E9qm7sW0KQuq5KkNpfB1KTCFIlngSpzVMarMGbZ3Zi9gqh2+minM2Ds9btwjxqamJ8STbqmyRAapMEUmL4nd2FufRTmYLwk6iQW2LZV2swvIcrZLT5k7m0mZtYrc2d+0zE2hUfwFBLRv9/hO37X/jfvddQbFq3VPK/GHKl3PpF6pHNABCA8GeGCCrBCSyZBoqPYNWl357wYlzjrnwxIkfagZV50wEEIi+2MYhR+zMRyEKQNaEG9V4Hc6nV4AL7pR6nFUtBLgK1n70eHFger19FEgHkG5IpgakSzxFd4M5cnAPZ7lC/O/0JO6pPBmdK38KJdE9UyX5+mkVtTCZ9vDvS1VD6POPn0Mwmdr7K/vq21393cc8IdnOLMj17YyXb3FtosCtcA2bsRaofmLVeqv+Mhh8G1bRqNPavaFGIyS5GGNmJSL2EgD3MxYAplAIOB6VLrEeP4NPNRofpeh6BRyYxPls2tA6gmC264QeTHZ1h4+kUT2P4E5yL6TvBWAdzd+xGUKk/RIf6Lw3mQ47zoQ97A3bx/0EnvbDzHFPfoNQi6XbuZvQDCwjmZJX1u//Fz4R0sPt+Mll5hTTnr1pPjddkVVkWgkKi2TBaBU09c7g5NdSxqlGGkKBgFMiU4OnpjpzEGBTLa8PG3BBp7HkqqFBGKxvzBptrUmQIEvi5l7oWAdilYfd6YVYankTGoZp6lLOLG3SZAtWOrIxYREanw8DKHnYE2bCwJFjZ2UOtqgARMckwtiCzqfeReGUJmXBQJMpYQbd3doHR88279n4VpfmIjk1pcl1jH4QHB0l9RTqmNmhj8+K7SLbnIvThExQqaMLDxYFfH7y4MoMVzOxiOdjZWT5vTWBhLCYaVSp6km8aj9zMWIRFprOtoBUc2XxbO17lwyL6KbjWT63pJzLj+kP0q2UVFDexWZzzR/7/P/0+qSZv1XzgL+mBZ2QsouF0nKc5jgQmS5W5P/otFH/Jl2g26j/WA80g9R8w9SKtmslPVmz43V40GebWwfawav61KP8BM//3eMVmkPp7zOMfvkURK7Pi93NlMqUXFVEh5Hs+T7//A16/+RVfcw80g9RrPoHN5jd74O/ugWaQ+rvPcPP7NXvgNfdAM0i95hPYbH6zB/7uHvgvNfLGmmHr2DIAAAAASUVORK5CYII=[/img][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAb4AAAAYCAYAAACFv5iuAAAgAElEQVR4Xu19BVhW67b1oLu7QVpCSkAUxO7u2HZ3t2633bnt2gZ2NyoIqIB0CNIljXT3P9/1CaLoOeee899zvefyPo/7eL7vW2u9a6613jHHmGMu+RppoG38MhEoKK+BqLAgxIX4f5k5tU2kLQJtEWiLwH9SBPjagO/XuJxlNfVY/TwROaU1AB8wxVYFA42Vfo3Jtc2iLQJtEWiLwH9QBP4l4PNNK4athjREBGilbhv/UgTuRufgZlQJBAX4YaYoiMkdVKEuI/Iv7bNt47YItEWgLQJtEWgdAb56onwv4vMR+KkEopy89nMQY9/Q79FAf+obAP+kIoy3U8VoS1UItmHfP31/ZRbXYPmzeNTU82G4uQImdFD5p/fVtmFbBNoi0BaBtgj87QjwFVfVNk69HQNpSXHU1jWgliHaDwYfAZsA/UdESACSokJI/1wKvsZ6jLFSxhBT5W9YX2ZJNdzCs1FV2wB+fh4isn3baErCSEEC2rKiVMMS+OnMskjuuxiShbr6Rhgri8NZRxaqUsL/K65lWmElroTnUHIAmKmIozPNXVmi9dyTCypxPTKHEohGxORVII/+iIgLoYu+HKopVnL099+s1SAj8vM4/aoB+Ux1ys8VtVwKJUn1So2fMNd/9He/6nm2zastAm0R+N8ZAb6iitrG+U8SoCojiayiUkgIt15o2QLGQC+7pAqKMhJopySFhNwydFQVwmx7zVZnfsTvEzziS6CjLAUGmHz0H376U1xRjcLSSmjLi2Kjqw4UaHH/0djpnYrQ7GpUlFejg6YEJlmrwlhJ/JePMEsZ/vBIRmx+LUpLq2CvJ4WJJFnqK4i1mvu21ykIzqyAloIkx7TZH5ZzVFCtjyUL8RmFmGavgqGUVLARm1fOGV60ZFvv61cKzPngTHglFxN4s+tOMyN1YEEndXShBKDlOBeUAe+UkubfkcILB0qMZnXUgKhgm7HnV7qmbXNpi8B/WgQ44Fv0NBHV9YCLjjgBmdaXc/xq9mSg9yQ2F7c/lkBCRBBZBWUQFxVBV/r9DDuNVjE58DYNccUN6GGigvD0AqR+JjYjKAADFUmoy4ojIr0IdVWVODDAgAPEluNyWBZeJJZCUUoURrICmGvfev+/6kX4kFuKza/SoCYvCRtlYUy1UfvpVP/wSEJBnSA66yshJC0fmUWVzeyYxTsrrxT9zBSwsJMWbnzIgVtQDoQI+Db10EEHValfMgQM9NwTSuBkqIwaYq3MMMwUgtCUfEyzUYCLrjxJ5cCBt6kIocTGyUARlaQKMHCUEhXE8/AMTLRRwijzNqn3l7zAbZNqi8B/SAT4Cgn4FhPw1TXyE5CJUcbdmsFlFFdj55tPqGoQgDhfLcopm69p4IOztjiXoX8/Dr4j4CtqgK2WLJ5/SMcYS0XuJ7ciP0NXSQbWWvJ4HJmOCZby6G/01bn4ODYPR1+lgo/SfwN1Sezqq09SWWsGGplTytUa+UlMqyOpUF9BnCRBweZpfC6vxaeiCrRTlPxGKowm1lRVWw8Dklulv0iI0cRcq2iRNlORQiWxraTCCm4/hvQbqRYyIzsmk4ENiaG1/LzpoIn5FdjwMhkF+ZUw05XBnv4GVPf8eeFzi2cyCmsFoK8kCZ/YDIzroNycBLCUg4GfrJgQScPi+P1VEiQlJJFLLNJcQRAjzZXRjj5vGlml1WB/BIkpsrhICgnCUPFbhsybfyOs1KVRQPFJK67kGJmMiBDayf+YRYZnl9Ah+LiarhTt0+C7fba87uz4y+g+cjFW40AvLC0PJZW1cDVVR2lVPSLScnFmuCnCskpw6F0W+lloIDa7GHklFfR9Lez0SC4nkPzw6TP29TOAvNjX69nyOBUFWbhz8yZuPfNELV1L4059MXfaGBhr/H0HbOCzi9h7ORTbDu6AEcnQf2/U11XA08sXijqmsDbUQKTXLey56Itthw5AR+a/t6j96tYJvIgWw5bfp0D07030y/eRXrdx7kks1m5ZBxWxf3x+YR438Zd7ItZvWQMl0X98u39wWr/kz+6e24OIonbYtHwkrSP/cyPg+UXsO++O4dNWY2zfDtxEKsoK4eETCDMbe7RT/VYp+WdnWlOYhM2b98N10hr0tm0iNz/fW0REILKKhdDH2arVj64e3gDPDGXs27oQsiL/9fulIi8OW7YcRt9ZG+FqofrPntK/tB0HfEueJdKCScCnKw5bdSnEf67EaAte1p1Ktahdb9OhpSiN+JxiTLZSwI3IApTWNBJDlPgp8CUQ47PWlIVXbCaujGrP7YstvhvdkzHaXg9e8Z/RnhbxJU68i3ApNAuvEovRSAstY4Fs8ZcV5ceGrtpQlvxaIzsTlIkX8UXU68YDxBpiDCqSgtjUTReKEkJgoLfmRRLyCKzbUX1wVx99rv54g+ppV0NyIUgymracCA4SMN0iJnUlOBfCtC8FcQGS3Ro55suOLUa7H2mhCDMlCRwLyEJWWS3qaEEXIxfPEGJiQ0y+LrRnSbbzSSFgIfIiQvtnQKEoLoj1XbVovz+uTf5BwFdSJwBdAlgGEueGmbS6kKU0mQWP4wiQG0g2VURhZQ2SCKhr6uqx3EUTTpRYRBHL3PMmg4wxIEco7yZk85xorYgBX5IKxsQefMin8+SHEsWonACjjhIXJkGXkpw810kdfQ15yUnTdTodkI0CAqymGi3b52RiYy1/13LCR3w/UbJTD0sNGbxLyMGu3noIzy6lOmYhepqq4G5wGlZQPJ7FFiC3EpCjecSk5+M0gWFQRjHO0XUYT/fFndBPGGshh8EmPIm35Uj+8BxjRs6GiFZHjB83AMJ0pYK97+Lh22QcuXAPw12MWm3T9EEjCjC5a1eIdF2Lw5vHQfxL7fmnG7B7KzcEJrb9sPNGGMY4qSE7ORLvP2TBpXcvyP0TD/zfOtb33x1dNhB7nssjOuoSpP7BtcX97CqMXPccYQnh0Jf+BzeiAz85vhTjtnojIj4YupL/+Hb/lfP51X67fqwjHmS5IMJ7z/8Y8KWGuWPUtE0YNGYQbp99gK1utzDYXhfJ76/BbtRWvAqMhLXK/58af1VmAMwMHbHoSjgWD7P4u5djUt/2qHPYjKt/jP7mt2VZ79HdeQKm7L2KOcPs/6nYlaT4wNzEFZvux2JGX8O/O5f/jh9wwLeUgE9UmECjpJwWOgHOmDHcXB7jCI2n342BpbYisY1qCDXUYK2rNuY8SOCAsstPGN8BYnwpJQ2w05bDw/A0zKcajzgxhtLqWlyNKEA/cw24R2ehnYwg1rnq4k5ULu5EF8JBVwEp+eXIp8XYUU8B8bTI55aU4UB/QwI3YZwKzEB4bg26GykjgOQzxvY6tVOEf3I+CkrLOabAWNniJ4lw1FdGYHIuTg815lgjA5rCGn6qGcrAPSoD18eYgdXZCmr4iIHK4rpvMpSJzRkqS0KT6mjlNXXkWv1MLApo4BOEviLVNukPm1/4p3zs62tA9TYRBGaUYOfrNPQ2V0ccAXs+GTscSNIrJLaTSzXTDVTLVPqBuYXNp7xBECZ0vIdhacT8JAjweZe4hgB4gIk8DOTEsfhhHHrQvrXkxDjGxq6DJ7U+jLNWwCACh2l3omGtowRJYrxvE/IgTv/biWIXkFKAQUbS9BslrHZPAL+QKHcOd/2Toa0my7E9VRlRMg2JwiMmGyucNWBPoFVDx1j+NJ5QVBj2OnLwS8rn5EindgoISs3HYGMZDPhBf+HypwmQIoMUY6lRBGhnCMhZXXKjRyrGdtQh9pKDHnoSqCQA9aIEh4E0Y85rXHRQRbFe9jwZo2y18TAinRIwKcz8TkKvK01Df8cOKDGZBc87u/GVrzVi07TOOOori7iwuyhKSoGkggLSYiNRIaqMTvbmHGOKCfDAlUde6DtyJrp00P7mWSrJy8D7sI9ooGRA07ADzOieaqgtgdeDC5g0eyN+23AK00b1IlOWANKIpWrq6XKJERv1FUXweReImkYh2HVygYJUE39oQGxEOESU9SArWID3wYmQVNFCJyuTny4W8R9CkZRBqoipPQLclmLXAxH4+53ggK+2pABv/INRS3DPO05rgPK49DtmbveEZ5APdL98X5CViqDIOFKT+aHb3gbGWnKt1pEX5zZg7r43tJ0XdCR4+60p/ow370NRxy8CRydnyIjzPi/KTUNSZjksrPQQ5ueHwnJ+WNg7QE36W176MSwQaZQoG1o6Qhp5yCioo/WjHMJyGjDQ5CWNtRUFCP+QAk0jU6h+qV1XFuTgXWAEGgRE4dC5C2S+MNfCnFQkpJegvaUFKGfiRmpCNIpqJGDZXgXRESlQUpPDx/BICKvooaOFPr7XDD4Ev0fG5zIYd3DC3V2jcSveBu+e/NF8PT4EBSAjvxhqOiawNPnKisrzs+AX9IHmJAhLx85QbZGItwxmY2M13vsFoph8DOKyWnByMAG7TTJTEulZFwN/TQ4SP5XC3N6RWpWEkR0XgIt3A2HnaIqk6GQ4DhgCE7kG3Di7HQt23cf2wycxsHsX6JAaxUZJbgb8Q6PpWZZEp66dINECE4vpu/f0HXturel6KYl9y2OrsoPRqWM/zDnhhdkDeUSEjfTkWETFpQF0ndtbOxDBEUFs5FvMmTgKfObTsW3ZeNjbtm+OpcfdC3hDyetvU6ZBn+LNXcfKQsTS2qNMpayI0CjI6Jqgo7EWPUOl8PMPQVlFDaQU9eBka8A7jzRfdO40FKsu+uG3nvrNcwn2fYfPpRXQNbKEsd635Y4Q+i6PvlNqZwQbQ52WYW/+e0NVCXwDQlFOBEFaSR+dbNr98Hfsw2bgExcRphu1CIbqcuhMtZeHVG8xoSAUVvPDVE0K7xJzsc5ZG0p00ReRGYYJjZ20qCb4A6mzCfi6Eot4HpXNMZSmiiEDwzRikRmFpVjVVQfmtPDPfhALMw05RGUWQ4i/ARYqEgjJKIOBqgxS86vQXkmIZFEVzLoXh8md2xEg5ZNJppxjgvH51ZCg+lBqahH62apiMhlhFtMi7KCrSAv1ZxwbZMQB307vFOTTuVhqSOHlx2xcHmmK3T6pHPvoQYzkEZ1vVS0tK3S/CNAN3tVIBZkkB/oR+GnLChOg1YL4DyY66OJG8Cf00JXEcDNlSgLi4NhOiWSBSi5xaE8s059ubns9JZTRgp5dWMYBstB3DIOZYMpIOu6sr0DnWE5JQT0HRkzizC2r4YB8V299mncqMslU5ELzySa3bFJuMVcPc9GVRQk5SHxSymBLxpHCkkr0NZKBd1IxUkrrYUVs+31SLse2N5FUWscvxIHXg/BMWuDr6TiNdCPVoL+lBu94xeXYTyz4KBmTkoitdzGQx0ViUv1N5TmwSiqqhbW2PBe7pZ3VOZBsOdaQVCYiJkoJighCKO5nCfgiiPHt8E4n4NNGMtV5I9M/4zwxvJaD7XsPnSO/iAjFng/JeSVY0Vmrlawa8vQYHIf9QXXAJHQ3kfx2HwWf4BeZCodORljQaxhC6HyEhRqg7TAJVw/OxfX967HjLw9oqCqiqigL2k5TcerAMkgL1eHZ2b1Yf/Q2BImZ89WXIie7HjM2HMTa3ywxe+xQXHkeBm0Dc6zfew4WdW/Qd/YZeEeGo70iP9KjPDB92jKkV5FLmb8CVVDF3rPn0ZekpEZUYK6rA/yhDAOSs9NSs5GRFg/XKdtweuu85sWbnUhjXRlO7ViPA5c9IUvJjpCgGsSE01Ek0BV+HvuRE/Yck2etRE6dOMQFq1Ffr4Q/jp/BQLoXW45m4Av2gY5kFe4e2YEt557RdSEIqCtBbh4f5m89hOWTen0Dvt8DX2LQY0ybsQb5fBIQJbCqF9PHwfOn4UoA43fnAIbNOwSnPq4oziZlJYkSOMn2OH/1Mrq2VyWArcKRDcvx500fyMlJQJjOha8iEfzajhDPfoN2w7fj2Jrh3LQLEzxg0WEi9jz1xfiueojxvYdp8zegTFASYgQi9YJa2HPmDLpTAv6aQH38mmfwifaHoSxvUd82vRvuZ7gi8PlM9G3fF/mknjSQbO4wdCmOrJ+AJutcfWUe9qxfjguPwyErS+ckQvJaXQKEtMbB4+Za2uYzdq5egkuvPkBGQgSNVeXoPG4dDq0djzj/l5i2cBXKCBiE6mpQVC6IzYfOYMIXWbIp/qlhL7Fk3jqkEcAJNpKrOTsXhs7j4XZ+C14fXY3VR55Dw1ACFdXaOHntIqwVyrBr/Rrc94+DAD2PYlS/7/nbOiwcrIYRg0bDKzIDxqYdsP1PNwyhNS/4xSXMXLYb9eIUm4YqNEi0x9ELx+HQTg7hXo8xZ9kGVFJyK1hbjeIqcew8dhYju3191r4HvvrKApzcshqn3CPITEYlo6pCFFfKYtex06j6cBHLthwHpLQxeMI8/LlrCQRK07Fx8QI8Ds2FCpVGSvNy6VnYhq3zh6A8wxeujjMgZCSLCmrNGrFoDyaYVWP+nPXIFZCieFQhLysPVv1m4syfayGW6w8H+8HNwFddnIp1C+fjSWgmpClxrq+swOAFu/D77AGoL8/DxuXz8cA3gdZ5IZSUFsNx0AIc3rYAlDs0j48k8y9cvgOFwnS8hko6Xj7sBs3DiYNLocAW9e8GB3zLiPGBmJ4rSZc5tGjU8AmR4NiIRFqspjjo4VJACvroS1FtiRZf+n7di2Q08vHDUfMnwEfmlpTSBgy2UEMOLcjM4s8YiSG5PN0CUylnraf6nQHHhJiZxTe9Eq4EttcDU6h9gR4WqvHFfS6HCTETOx153AxOxbbuutj8OhVdyDjBFkhvkkoZUJUQw3KmFgBX+sPVxQjkNtLvnAiM3icz4DNsBj4e45MmMM5qBr78aj5il4yZZmKTqxZXO9v+OhlFVH+z1ZbFE6pFXv4i1a58lkCuVkmSfyvQW1+Sa9fwzahCJwKhG4FpMCXAFuLmXkHMSwg9jJXxjI51brhJqyZ/BnwVjQLoTr/xjsvjapKsRsdk3goCzOqaWhwZZAxNagVgNb5GyuQY8PWh444w42VDrGXkXWoJkigT1lCV5NpECqiNIK+iDs4Uz0BiwudHmHDAx7Y3V5XmmPb2XrpQkxLBq4R8ar3IxwgbDdwMScciR1U8+pgPUTExekDrEByfS7VWacjRwvmBQKybsSrSi6ugK81PpqNva8GrCfgkxcWgQvsNSM5rBr6dBHwTHXWQSOw9KrMAp4Z8lXQZu2SsO6eiAUOtNHDKKx4D28tjGrG972/VsxuHYOWVfER8fAOtn9ShGlGEiZ1sEdDYGX5vL4HeAwD/ewcwavFfuOr1Gs4E/HWliRjYtTcsZh7Hnjl2mDd6KoxGrsTSMc5cTE+sGIjVt+uQlPwcUtl+sOw0HFuvBmM0ycFvb+7GuFU38Co8CIaiuRjVxQ4FBtPxwO0PSPGXY934nrgapY6AgNtQFqnGwm52OBdLph13d3Sl0kHQvX3oNHwzbtJiN8xBvflRfHd7H3pOPo5br70w0F4bCYFP0KfbIEjbr4P/08UECh2hMHALTm+cxG1z9/BirLkST/t9SPXZr7ymCfi8InygXpOMGRMWofPMLZg5yIbbbsc0FxwP0MCHyGuQbUEYm4DPO9wLanVp6NvRFqIu63HjxFKI1hViwRBXeBZ1RMi7s4h/egJWA+Zj3vab2L9uJAQK0zDYtSOqbdbA88JSeF/diT6zzuO+92tKADQR5XMTfbqPgcGghZDO84LukC04snIoD/gSPWFrNw27n/phuGU1ejk6wXrmMexfNIz7/uKWKdj7qho+ntcQc2cbB3yvQt/A4Avw7ZzdBw8yneH3aBapBPpocFoO96ubIU6JNh+Z6ZrGw+MrMH7zK7zweQEnUknCPC6jV69JsBi1G543VuEOJUerLiTD/e0TGEgLoDjND916jceSI3eRcGE6Hpb1RtjjXdzuDq2ehShBBxzfPr0ZWNnnNw6vw90oSbidXsexo/QAN+g7zMH9iCTw+e1G/0W38TzEF73b8667265p2HL7M9y9H0CXWHZBog9c+0zCmktv0VPEB7ajduDBu3DYqAmgJDMUvbr2waDfb2LDRFfaugGHlg7DtUQdeN09hCX9DBGhMBV+1zfwrvPiKchS6olDGyZyjJON74EvP9kP02bvxJzdJ9DPWoNW+ypMdrZArMIkvL+/EdP7mKChyzZc2DiStm6ke28MDnsK4IXnVWiQzJ8V9QzdCFi2uPlgmEkRzDWtYD7/GK7tmUPrewPObluKd0WGuLBvAXf8KPc/Ydl3C17EpsBZNhq21v2x6tJ7/NZDD3+uGYYz/lJ44XEJTNlND3+E7kMXY/+9AJjm34DRgO3wTfkER1UBxPvcwext93Dg3ElYafES4EbSQY5vXITwOmuc3jmL+yz00X7YDD4Aj48fKFFurXJwwLecXpVFjhKSoiSJRQniGtVlxttpoYykyYjMEqpBFeDCyPacIYQB4zoycYCAz16duUBbm1v2E/Blljeip4kiLr9PgzzV6j7TYixI4OpsqIAkAgYzRWFqU1DjGA2ROgwwV4UfAVUCfccWf8aQ9FgbAP09OLUA18aa4fHHPJJK8wjUFFFBdSrmGpSlRTk8vRhKVFNbTkyBGVVW0Pm4GCoRS/2M4wR8rEWDMb7iWn7YaMngUWRmM/CxzyyorvmUAOoigQQ79g6vFJTVC6ADvZXmyYdMTi5lFns217J6fmJndehJsl1sXhXJp3x0nrxjsd483tz5uXmJ0XFjSBpjwCf2nUV/MwFfPb8ggaUkPRwZmOeozgE3G6z2xv6mIyPGAR8DLiFiRFlUt3QlJ+3oLwXhFDrezag8qslWcYYgfromzHHL3J9MKo7NKcEZmnvT9poEjG/i84h18cAnnpKLDWQmmtlZD1eD0jHSTBbhWeWopcSHxT6Y3szDZE5mmGHJiCG1lDBmGkcS1kW6H1q+sIcBn4wkAR8xPr8kHvBFMsbnk46pnXSJ1ZaRpJqDgwOMCHSFueu3w4uSIDovNtd7YRlQIEAbaaEEqx+4Vs9uGor1V8sRHPUCmj+przWiGGMdbCAzeDdOr2cPLLB5YifczzbC9iWjSVKtgYCgCF7+tREP4ozxMfIqJyOmfoxEcHQEklITcPuyGzErC7yPuAPpT29g6TwSmy8FEPjo4N2tPRzw+cQFQSL6HkxdFuKafyx6mfIewPJUb1jajcWOe8EY04XKBF3MkW4xH+4n5nPf1xZEwMqkF+aefoUFQ7/WWdaNc8BboZHwubTyyzIF7JrmiptpnXFlvyP69Z6NRbtPQl+mnq6FAPhK4zBuylqcfBGDqb2+SkVNwOcR6AO9LzW+hIgQhMVFITE5HtcvXEG1TFe88b0AhR8An2+0Nyrenof14O14HkFKhhZv2cyLegQblwW4EhINpY8X0HH0CbyNj2iuPx1e2h/ng9sj3Gcf1oyxQ5jiDDw/Nqf5XDaM7gzPUlMolQVywHd4xRDuOwZ8dg4zcMgjGBblj+Aw/HdsOnAU6qK1VF4QQF1eKMbN3gf3eLo3PpzGiGX38TLEpxn4ds3pywGf78MZcCWJut+Wh1gzzr75uLxFsQJTe9ihrOM63N41sfm7pf07IEBoDN4+WIXJXYyR1W48Fo+0pzo/SbLCYjizdTbKDRdgrFkUluzwxOI1q9HDpQt6OvMMKD8adcV5cPd6QypPGrxfuePWnXDcJ7m4xmsLVl3OgT8lRMwTxerNI+2tUWU5A3MHW/GOKSKKP9dPA5/jbpycQ475YVtwyysYDjqilHBtx4iVV7H7wF7avporvZSmeGHqshsISItBwNFxWHU2GstWrUI3l87o7mTeano/kzrD/N4i7lMComKiuPtDs/NieFxZQ/eVMeo6b8HlzWPQUJOFAZQMiTkvoc9NqBxST8+tEPYsnwSZ3kfwYE9H2Bh0wdIL7zGl11d5sfxzJjzf+iIrPxWvnjzGw+dpeBIcCWcFHvCtoYRyfFcRKhNZQqHXKkxwNfiyb37sWDIJmsPP4fA0GdhbD4Lp8FmYNXwwnLp1gYbcj+1epbmf8NrXH5l5qXjx+CGevsrB00A/dKdk+vvBRwyhkQEFH4FSZ5Iup9qoY9HjeEJTeXpvZBXKqfdugrUKTKkGxQaTphY8iud+b6cmhjk/Ab6cikYCKGJrIWm4OtoM2awpnUwWWZWNGGWliVO+SWRxV8LH3Aokl9SjJ9WNLgWkQo/qZswgwowmoSRf1lbVEZuRwtIumuRWFMCl4Cyk0b4YsKQWUq8c1dOcyPjxp08iOURlMby9MuY+iqMHQYlYYR4ukaTJBpM1GcjZaUvjHrE7JnXuos/K6vjJhCONBxGZODHYiAPJ7QR8lSRDWtHnD+nzk0OMuR46xk4YWDFW1V1XAomE2IW1PMZ4NfATDKg/UYhDAz5E5ZQhn2pculRTXNJZk+RaXvyaBgM+CAhxwOf+MauVBNjytwy4RKh9JKOommOarLfvE/196dM47jpp040QnFpI4AS6TuJ4mVBETJnqHeSgPDuMB3wMYHRJonD/mMOdOxssyVj/KgXzXNrhMs1/CNXvIrMrICAsjHICuCySPxn4MhRmYB+RUoRGMvAYakljmZMm9Fq4QVcQG1YmGYnJzwxcGdjHUlP+Jg+2f30u5hqSApjjwGNzLJbSBJSOdP3uEuj1M5T+xuH7/Y3qcYlMACsfIORjKEzkv+WDTF4LjYyCho4GlvV3gVT/7Ti5fhQtMNVY3rcLbidWQ19TgatdsyEiSi9S6DAIB7dPwIXd87HzrC80tLXIyOIMibIQPH4vAL+wewR8PgR8o/D7xff0UOp+Ab6blOQEofL1afSY8Cceh4eiwxcDQk1uGGxtB2DuMU/MG2yMGc5mqHFdg0tbf+OOW5MTQt8Pw7wTTzB3EG9xakQNZne3Qr79CtwhFtA0Lu2Ygj/fqOLIaksM6zsf7RztiEmQnZrdXfzCkJJQxdKt29GdnqWm0QR8r8N8oC1UggMbZpDkGAktOjczh65oyPDBmwQ1vPG7+OrjzEcAABa/SURBVEPge0/Al3pvD4YtuYtXEb7UTsSLc1naW1jbj8PeZ6EwyL6BAbMvwT3UDyYKvO8PLRuKyxFmCH61FROdjCA0aCcurB3VPK9ja8fCLUycgC8Y7YZuxcHlg7nvipO8YEvAd/h1ADRTr6LLqM3o4GAFAXoxBhv8AiKkImhhy8lDqPE/RknHIwI+b0oAeMfdM78/7n3qzAFfNyMr9PvjHlaPc2w+Li++nzHExg7ak47izyWDmr/bu2gA7qd2IeBbgBHmFvjArwJ1efHmkoyYuBSc+8/G+gUDcOPMOhw89RQhVIvXNTbEnHVbMX9Cb7R8oWDwq3OYNm8n+GSUoK5tDhcHVRzd54YzL31R570V69xy4eN/C/L0LDXUpaC/WRekiGlBhZJR3uCDOB2z58glGGCWgV5jd5ICEETPhxienFqH0Ssvws6OEtYG3gtGBARFISFhhB2n9pKS04iLf27A8fMvEBr+Cfrt22Phpq2YNapbMyv9HviqSF5cv3AKHvjnQUNdEw49ehKbuo4ihRF4fX0tAZgx6p3+wOU/xqKuLBY9zVyQp6APRemms+aDhKQUeo9ainlDFOBg0ROLz7+l7XhmFZ/7hzB72VGIKatBU7cDHMzFcOjwI1zzCYGLwkcO+NZeC8M450q4aDugUMUECpJN4jQ/7VsSvUcuwpIpPZAUeg9rSKL3ex1DUqYYBgydjD3bV0KHXPtNw/POXsxbeRISKuSHaGcFOyNBHD7xAtc9fNCDzIjfDw74VlK2LkBAJibQiF6GsniTXILQxELoaTBZTYkzIrAMnd0VLON/GFNAdSYqoqr+GPj2EeMjYyhcqE50NSgNRyjLlydGVlRZx9XzZjrpwY/MF4J0gw9vr4hdb9I5WfQxOeaGt5eDOK3g79PKEErsQ45qL6wetbyzBraQhMkMCEzF2ENuzXiSHLdQPW8IsVPWTmCjKkpuQCXMJLfQZAcdYnbZ0CLpwpTk04tBWeikr0hSqiRuhWZwgLiLGFwFAZwNLeRs8W0Cvm0EfLWNghwg3qXaX0vga6T6HwM+J00xmFPRmTkqh3VQw0NikSMpwCKklxdX1sMjqYRjS2JCfNjdp12rN9X8TsAnICQEK2KV598lQ4WYXVNPIzPtSNEbT5aS45UZaDa8TIKclBg+EdBLCDRggKki5KjOt5VMNSu6G+GAVwLFjYG+Cq5FZCMkq4pjq55xuRy720jbC1MNtweZgp5FZ1Phm48kMlF4JhZBkupyfUj+Oe2bgp760oihoqe8tBhkaP9BxLRHk7OVEVHPxBKkEuMsp0REVpTMQj3bcWy0aTwn6fnmhwKSxrUJRNMoKRJHQkEVt/9uVOv9630qAZscjBTFcCUsF8rStBCSS+HRB6oBkyW1HQF2NRmTWMIziOqKw7407jftP4+kIFuzbph97h3WT/h2cYt9fQ6WgzfC/b0Pri0kNtHtd5zaMJqTQFYOsIOvxFj4Ui3n+5Eeeh8WDuNw8EkoPbA8Fnx9xwQsu1iI8JinkEzzIuAbg21Xg4jBaTUzPu/YIEjFPYCJ0xxcfhdLrRm8emdRnDuMHcbjhPtHDLOXx0xiB5XOq+C2YzL3fTUZDOwY8J182gx87PNNEzrhaUkvBD3a0jzFbZOccS/bGee3WcPZZTleJifDgWSvvzWagO9dzBsCCjeYdl2Ayz5hGEFSMxsnVw7AXg9pBAZf4xbgptEkdTLGV+V7CR36b8KT8Hh01uUtRJnBt9C+x1I8iU6BTMhx9J97mWS795TM8QDo4NLBuBLJgG8nlg2xRqTKDLw8zWO5bKwZ5gifKjPIFvhDf/QuHF3OA6Dcj49gYT0V54MSYZh7DR0GHaR79yNMSUr/fry+vBnj173A+/h30P4ida8ZYQPv2pEEfNM54Ou7+S7WjO/0zaaNqMTMnrZIN1yI5yfmNn+3sLc5QsQn4O39xRhibgDZ0cdwaRNPYv06qJTh5Qml9s5UphFBDJmVXt46iMW738I7OpDKCTwJrbGRygW2Vqh0XIlnxxdxn5UlukO3wziqk39Evc8WrHXLIeC7zSUcjfXZ6G1qAf2Zl+ia9Gt1rpHuJD/OPY77BBJ2mkLwvLgBQ1a/QFxWANS+8zSx83v7+h20OnSnxJYf0WFheOK2A2tPRMHv43t0/CIHfg98Xld+R7+Ft+AT7oeO2rz7d8kgSwQKj8a7OxswqachBLruIKlzFNXc0uBiYoVOa+9i3xzXVvMt++RPZpXBWELAN7W3EeqryANhaQWNMYfhtpXHsjODrsOo61Lco2vdtYnxXQvBeGciDlrm6LX1KbZN/fbase0+xQUjoVAM3Rza43NmOkKCvDF/4mS4rr6JM+t5teLa0iR0tbSB6YxTOLd+DPdZytuLMO+7kRh3GIH2Txjf8ucJXM9dHLEvZsVnshYjLixBZotRy3+4iGXNWpSlMEOEoZww5lIG//1gwFdKTKg3sbgT75JwlIBPjoCvmmo6TEaUEhehh0oex8g8cZEAaBs5HCEoRDUYedyjhZvNgbkzuxJwsmN7Ug1sbAclXKAm7rnOeniTWIDorGKOXdA6jHG2VKOiWqGqBD9m2alTC0A85pB8x/bxOCqHcyrWUabE3nrC6nFXg9NJ1jTlpDbqb4AjsSO2MJ8kxsdAlwGfAM3Hnow4jIWeJLmQSZVbiKWIE+DnldbCghrUJ1qpYSXFjo+MI670EDyN/kwx4x2rJ7USFFGh3SMmFxu680w8LQcDPlECowGmqkgsKOXqhU1DjJjtTWrvGGAsS+/tVMV6as8oreMjAJHD67h8Ys9V6EN/fxFfiEn0woF0an7/QJI0G6Qoo4ueLLnhhLlEogn4xIgxdjMgZya9PCAis5TrMWQmmWEkm3on5iOaJNnt5LBKp30f8cvERDtNhFLtMIP2zaRX5sDsbqyI+1RXlKeFZxGBMnPaNo1P9Lt1xB6HWqpRkiOMlzF53L0zgv6/PwFo6KciasbXwB4feigoOelGNdgEkj9ZPZPVRZlEze672Nxy+lPCXZ/vx9nNEzD3gA+O/HUZ4wZ2pXouH0L9H2P2+HGQct6I5xeWYbKTMSQG7MAZqkmw4f/gMFyGbsCJe+6YPtSJnHFJWDd/NoQcqa4zQBrmVsOw+1EgZhDwRfs/xfCRw5Ap3JGcbm+gnOcHY7NeVHcJxBxywrEa39iV1+ERHgxDyQJM6uaABNkheHBtPxQFPmPN1OG4Ha8F37dXoCpWjemdbQj4VuParincXKqzg2DTYSjmn3lOjPCrHBX67Aychq3H0dtPMWOgHSK9b6J/37FQ6LQOQS8WEYhaokB9NG5c2gtNeRG8cNuOTafe44TbFXIkSzeH6dVFqs1s84R/3DvUEfAZuS7CX94kuzrqIszrLoYMG4UGrX4IDHwE1RZysfu5dZi95w3eRPpAozETQx07osxsNm6d3QTpmmzMHzsIb8s74v3rE4i5vw/DFlyDezj1mX0BvgOLB+JShAnCXu+D/+396D3jJK48fY7BTvoIeH4BAwdOQ4fhG2Eq7IGXiaYke52GkkA2dq6cgs1ngvAwOBb9TcrR1coC4h2X4vKJPygxqsPDU79jz60kXL5zFQLR12HgNBuH7vth/hBzqtPdxKAhY6HXdy+8b0+ktcKcGN8DrJ3g1Oq+8bi8DQPm/oXrz55gqLMx3j0+ib6D5sJ25G543aIa36H5GLPGHY88nqFfZ0PkJAdh/uzFcJm5FZ8frsWFcF34+/wFDVo/3tzYit5zr5ADNoAc5TzAaGwswgg7U5Q7rcb9o0tQl52IJfMn4/zdd7j3/hP4/XZh9ZVMvA2428y0r+yehmnb/PDU4wl62rdDZqI/5s5cit4LT2GIVhRMeq7GQ99wkunkUJoZhs4dO8J0xF6c2LWYau5VcNu3AmffNuCm227sGO2Ax/lOeOd5EiqUTL44vwZD1z/FuyA/WGvwlKYquvccbHtj7ilybNK97OX2O/ouugnPUF840Tr34vYxDB61ANbDVsHv7m5M6aaPfMs1eHR4Jrf9qd/HYPGfMXjp8QjOVtpIiyZ36JzVGLbqPKY41cHWvDtJnVQ37MOALx09LU2hMv4YSaWTUPIpBrOnj8Odl5F4FPoZvTUSYW3RG6vdgjCJ1fjWDsfqv9Lw8tV9OJlpIiXSA7PmrcWETVfRUcgTZt0W4wqx3wmupKAUJsDJzg6d5l7C0RU85aC2LAWulu1hOPM8zpG6UJAShelTx+KRVyIeB6dggE3r1iiuxjf1Nmmu1EogRx7thiY9qNXt8/UDJkW+ogXYnl4xtayLdisjApMQI7IrORkvhOqDJ6ne07RI7nlD9uoMck2RPOhNL8dmvXLdCfA2ERAwFsnMJYzx1BJ4hFOrgDzNqaklgPX6vSArvKWaNDLIZMEWSx2y+eew5m2+BqoZqpDcKE6tEblUFyiCpboMmWoEkE5MKYaAkjELM5IGEz+XwG2sOfbRPGPJFapHx4zKKMJZWmyZkYPJkImFNSTl0edZRThH9SxZ2g8Dq1RyN1bUUo1PX4brYUwgarv+VSK1QLB2B3rfKS32glTji6MFvJJqSl0JhCZatW7SXEdg9qmklmOb3/+LiCy+ntTMz1oaptmqgzXeM2mQsV0LclOGUU1zIBVs2aV6QuybMeus4loUkI2XNYMz+7AhOWLTi8pxiYw5LLGQlRTlWidOeCVBi1yGJqoSFDPKELPLqO+PpFsC7jFkwGD7fBr3Geeod7GDphwUqebLPmPsNSitkObQgGMk/f7I0s36NPcSe2exUCPLFatURlOdL5fs3fMI9FgydYDMLl0pIarh4sQz8zQNJhOnEkvMLK7ABboW3/+rH0y6vPTnPhw4fYnqkOR+pP3Xkk2//5jJ2LhiAdWgSzHG3goyJLU1AR8zArgdXIutxx5CREIUlD9AWd0Z+45vhg05c0+sm4s9559ARoUAW9cQHcmZ6HbpBdy83tNiWovFY4bjqm8mFm0/gQHysRi68DxeBgdxMl9uoi/mzVhG/alVEKXai4Rye+w+fhzO5BJmtaUZnW1R6bIaV3c2AV8wbKwI+E4/+wb4WIp548QObDp0DaLkXJNWMoSseBrd4454730IuR9eYcb0laRw1NKLDMj11iCKaSs2Ys6E/s1tFSyGry5uwoxtHvAOewst4ULsWz4Px8ldKaOiCkUDU9i0k8C1W4G46/OWkrqv0rv7ufWYs8cHXlQ/Y+0M6VGemDVzFZJK6iBMDkJ5bXvsPXEYHemZ9b29F6MXX8cLaldoYnwHlhDwhZki0GsvJ63dPbkd6/Zfo3fPCkNOzRSSggmoUxhLC5wNpo2ehtRKMmIZaMJaXwOP73hj903qZ3PWRTwB8szZG0DLAySofaKhQQpz1/+BGaO7Q5Actwc3zCF37mtoqqrDwMYJtSl+KJIbBa/bk+laWXwBvtasgcnJp3ZswP4LT0hOFIWCpgkEq6NQKzMKr++sJwZWhH2rF+EUtRZIUHtPHd1XxlaDcejgashXJ2LmlOmISKVkUUQc/PQszF67CzPH9Ww2jnAJ1tO/MGfhBlRLKkFGVhodnbvB/+ZZDNl4GZbFJNVdTMebFsDXUJePXXTPnn8Y1nxMM/sR2L9nJVQbUjG4X39E5Qth7f6LmDu0I8LIVDJnyQ7ubU/ijPE2yGPZtm2YNLAT8hMDMHPGXMSS0iNItUIBqo8u2rgPk0a4NK/NjPE52BHwnXzDAV9VcQrWTpuCuwTMcuR21jK3JXk8Gy+DauDn9wjvLlMStfw0OgyZjuvndkC+MQd/LJkHN/cYmq8IFyMb57HYvX0p5CvD0NGmHwGfLwd8bLy+fQQLVpAhSEYF0vLysHemOu/FM/ht71Ms7cUHK7OeWH3Jn5ilAbUEZWDDwrkk7ZJzk/Zd28gH++4TsHPLYqhKN+L87tU4dP4h+EWl0FjdCHPXgdi/exO3xjSNl9f3YdHqAxCUVYGUvALsXTpRAkDy8/77WDH627ov24aPanaNf1LzcQHJkP9ATy8vw2Eb0h9dkssY6xH97p8lekkMwpPqTGxRE6ZFfLCpAqypJYKNpu8Evix6GjR51hKRT/LhI2IJH0lqY9+xmlofThr79u0rrG/ucUw+d3zWXM3ettJBTQL9aTFtehsLOw773aOPzPnZgE460tybTB6SY5HVrphRZaylMtKoTeAVsSa2H1FiG8PMFTlmxhb+N/S+STZ/9tvh9LkZff7ky+eMLRkri2E8SZzs1Nnc7xPYxpHJhC3erN+uIyUF/YghSfzkZdyPYj7DN7WYO9efDVNqjWCMjw3WmJ9ODtkgavNIJLC1IhmaAZU/geDD6Hzu2imTRm6nKcXFntVimUX6N9r+L3rhtwwt+ka0vxtkGZ5hpwb3uAJunp20pdCXYvf9NWSvX+McowRETHhijL2vkTxZiAW5ZONnI5Pk0PtkQmKyKBvOetJUJxSFMV3HIuptPB6QQS8sp9cU/Py0OdY9zkL5mxpiy+NVFKTjQ0I6vcScD8qaBjDQ4mn4xLWpt4us87T4aKt+K29kpyUhOSMXApIKsLMw/CZZS4oMI7cyuVVNremVekKI/vCRFkc9qr+Ik8xTiNCoBIgradF58Pr4dPQN6P7kzaixvgrBQWG8Pj5HW3K0NY0GpCVS24+4PHTUeC8HaKgtR3wCLTRq9FIG2vf3I/NTElLSc6Glbw15Aq5PebUwMNTiXIKN9BaZkJBIVJMwoGVgTf1WrV+MUPw5C5lUt9Uz1Kfrydt7fFgI8iju+pa29LL0ekR9SISqdstaDUm0ZELIonp1O8N2EPmiMjZUlyEolHrX+EVhT8lEk/hYWpCNT+TQ1W0Rg+yMZLLQC8OQgCzA8xH1TxrCTFsYqVmF1MdngyPzOsObbxQ8zy5FZVk2IqNSIKKogQ76WoiLiYWChi71JfJk84bKEgRHRNOVFICOkS3U5b6VPeNjQ5FXWIf2dh3BX5hO100AhlTjT4ylRVNRC2rUi/uzkZoYiwxqB9I3JddqXRY5zvlh1O6ruzY57iPFoRhi8uqwNv7a68mSmMjAD+QHoNjrGUHrJ29TKc5KwceUbIgra8CSzi0zNR6VAjL0sgNyWhfVQZ/6z77vLUyKjUZ2QQnEFTRgZfS1d7AsPxMfEz9BXlMf+uq8+6eGejlDo+PomgjDgO5VpRa9nI2UGIQHRXOlG119E6h/pzCxey8hMQ2yqrp07/GeX+bkjKIm+VK6umZ2tpCkBCAqJovqmKb0pqYGxISHoahBHB0syZz35X5KIJdkblEZJJW16Rx5sauvLkVCUjrk1fWgRM9608hPS0Ac9aVKq2vDTEednocY1IkpQY/emhQXl0LXvV2LmiHdq1GR9Canckip6MKi3bdkISMxGqmkBIlJKhNb/HF/Xl5KHBKyCiCrqQtTLVVaC6g3V5yO9yV+Le+Lf+nf4/vpHdb2xS8VgbXuSVRDkyDGJ4W/AtI440nbaIvAf0cETq7uj3l7I+AdEwJnqilHv3FD5z6zsPXaG2qL4LVVtI22CPxPR6AN+P6nr8C/4fgrybWbX1FPPXbCJM2WcTLij96B+m+YStsh/sMjUJGfjP2rluKa3wd6EYQ4vRFKDANnrsDaOaNasOH/8CC0nd4vH4E24PvlL9G/PkEm3QbS22SYpMvkz8HUX2n0N144/a8fsW0P/9cjkJ4ag6KyBsgrakJd5asB5/96XNrO/9eIQBvw/RrXoW0WbRFoi0BbBNoi8G+KQBvw/ZsC3XaYtgi0RaAtAm0R+DUi0AZ8v8Z1aJtFWwTaItAWgbYI/Jsi8P8ANHrSAxlV+AAAAAAASUVORK5CYII=[/img][br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAA8AAAAQCAYAAADJViUEAAACB0lEQVQoU42Tu09TURzHv+eeey/pw0EC0tLBVgSDjyguRhk0aHwMPhInBwZXB1f/ABfiY2EkGMIABhIXAhJFBh8JmlK0iUkjYB/YWkUwbW9LoaX3+Du9TOa28J1O8vt9zu/NBAmkTHEbisLks6YEBDRFgVNTqj4s/CsnhkO/kTJKaFA5me0lv902BbZKZdw760PPoUawoVBKTC8X4G92IbZqgDH76DLBg03u6uffVv7gwUU/2PNwWkwuGRCigtMeBxwatw29Wa7g4488LhzzIfl3A1/jqxY8sZiDxgSGbndAQa26Be6MRXDmcAtcuorJhQTYKMFTiwY4M/HkagDNLt028lqhhPtTy+hu90DjCqbDKxb8ktLmMPF4D/D5Ix7oBE98JnjkS1q8+m5QuiYeXdk98qVOL3RVwYv5Hfh1lLos9gZfO+6lWXOMBalmGXkmmie4gr7LARxw16/5+olWqplj5FPcgmdjeYDggRsd4Ny+2yZNuHc8glsnfdWGDc/twG8TBWQ2NtHldcOpW6v3v4plE3PxLO52+6HSig5+iIE9m0+J4M8ijnpow9aLdaYM7HdqOBdoRKliYuA9wcFUVjycieHmqVb0tDWRodZ2U2VkkvbsVhlPZ5eoT6Q30XX0v0uirWWfdRzWodlK7r6MHElkLFh6LaRzCCUNqNSweocpnWVXHDrHP4lr/vzDui9UAAAAAElFTkSuQmCC[/img] [b]Création des points de la base carrée[/b][br][table][tr][td]Penser se mettre systématiquement [b]en mode souris[/b] [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAACIAAAAjCAYAAADxG9hnAAAD70lEQVRYR9WYbUyVZRjHfw8vHQTxMMQiETJzlsw2B1Robc0vidO+xMhMmqU7QBhM6HB4OXAAEYwyCVkIRxtJIajxLhPrgy9rxScUEsbLJOTNDVDezjTgwNPz0FhaIw8PL9q1Pd/u57p+9/++7mvXdQuiOCn+dmOMqspxWpsFzGYQBBbURBFsbGDtOpG3tlrj7W2HUFMzKhqPj7HiaStWugmMji48iLU12NtD202RO/0imhBbhI+DTeJzqwV27Vbh4S6tWETr6JygsGCUW+0igmavSQwNe4qNG20XEeHvUNevj5OdNfYXSHyiHR4ei6vGNEpHxwSHkv9A2PehSdRLIM+vfjwgv7dPkPq/Bbl3/z72S5bMay4pUuSXX2soLi4hJSV53oAUgVy6dIWQkGDe3LKF5KREnnV1nbM6ikCqq3+krr4eNzc3KioqSEtLZe0La+YEowjkfNUFamtrMSToKS+v5FR+PjpdFL6vvaoYRhFIZWUVtdeukWiInwos50x6ejoaTRA7tm9TBKMIRFZBPhpZkWm70dCIXq/nHX9/9nwQOGsYRSClpeU0NDYSr499KGDP7dtotTp8fX0JD9s/KxhFIMUlpTQ1NaOPi/lXsDt375KQkIiLiwtJSQasLOwlFIGc+6GE1tZW4mKjZ9z1F0eO0tvbKyWxlhUS1KNMGci5Ym62tRETHfWQ//ZbHXRI38DAAANDg2Qc+ZIX16/HaMzBSa3+TxZFIEVnztLV1Y3204gp59Ml/+vsHHKOZxPw7k6cnZ1xdX0Gx6WOePt44bJ8+fyDfF9QSF9fHxEHwrl69Wep1Kdw5mwRQ0PDUl4kc/KkEVu5B5yFKVLk2/zvpkJ4e3lhMBhQq53YtMmX4CANB1NSpYq7kn17P5oFBigCKThdyOXLVxgcHCQyMoKXN2xAExRMZmYGQ8PD0m2KtygvHiRVBJJ3Kp8orZaysjLeeH3zlL+Mr45hLXXDcv2I0yfg6elJ4O5dFquiCOTixZ+kccPM9gfKeVd3N1FR0WRlZdLX30/KwUOcMObi4CC16RaYIpCZ/B7NyESlUrE/NARddCyv+PgQEOBvAYbCHJnJs6yKTheDMTeH5pYWUlPTyMv7BvWyZY+EmVdF5GhyLamrr5MKmJN0LA5ERhzA0XHp4oN09/SQm3sCP7+tbJautKU274pYGvif6548kCdm0vsk1CTqYu1wX/V4Jr3Orgk+PyyNnHsCTeJ779vgt02l9Jjn9F/1hVGKTpsRPjtsErs6YcfbNqx7yYbJyYV/H5GbN2sraGwwU3XezCp3KebIyKSYdeweLU1I1RHGxxcWRH4tkh9qVHZgGkHaPISF2/MnnrY52PsGU0wAAAAASUVORK5CYII=[/img] entre deux actions [br][b]Bouger les points ![/b][br][br][list=1][*]Placer un point A libre dans le plan [/*][*]Le renommer H[br][/*][*]Tracer un cercle de centre H et de rayon r (en[br]utilisant l’icône [img width=32,height=32]data:image/png;base64,/9j/4AAQSkZJRgABAQEAkACQAAD/2wBDAAoHBwkHBgoJCAkLCwoMDxkQDw4ODx4WFxIZJCAmJSMgIyIoLTkwKCo2KyIjMkQyNjs9QEBAJjBGS0U+Sjk/QD3/2wBDAQsLCw8NDx0QEB09KSMpPT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT3/wAARCAAwADADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDvNM01PE8Uuo6lJK8byMsMKSFVRQcdu/FXP+EM0f8A54zf9/3/AMaPBf8AyLUH+/J/6GavatqyaZHGqxPcXU7bILeP70jf0A6kngV2169SnVlCEmknbQlJNFH/AIQzR/8AnjN/3/f/ABo/4QzR/wDnjN/3/f8Axp0emaxeAvqOqm3Lf8sLJAAntvYEn68USaXrFmA+nas05X/ljeoGV/beoBH15rL61X/nf3j5UN/4QzR/+eM3/f8Af/GqeqaYnhm3TUtMklRInUTQtIWWRCcHr35rZ0nV01NZY3ia3vLchbi3cgtGSMjnup6g96p+M/8AkVrr6p/6GK1oV6tSrGE5NptLUTSSE8F/8i1B/vyf+hmjRx9u8QatqEnJglFlAD/AqqGbH1Zv/HRR4L/5FqD/AH5P/QzS6Owsdf1bT5OGmlF7Dn+NWUK2Poy/qKxxX8efq/zHHZFjxH4jsfC+lNf6iziLcEVUXLOx6AD8D+VZGmeKZfGVpu8OK1vCDsnu7hBmJupVV/ibBHJ4Ge/StfxH4csfFGktYair+XuDqyHDIw6Efmfzpvhrw1Y+FdL+w6cH2FzI7yHLOxwMn8h+VR+79n15r/K353uGtzMuNKg8O6ppV7aGRpJ7j7LdySNuecODgse5DAY9MkCrvjP/AJFa6+qf+hijWmF7rmk6dHy8c322XH8CICFz9WIH4H0o8Z/8itdfVP8A0MVeF/jw9V+YS2E8F/8AItQf78n/AKGau6tpK6mkTpK1veW7F7e4QZaM9Dx3U9CO9Y2l6lD4ZSTTdV3QRpIzQzlSUdSSeo781of8JhoX/QSh/I/4VriKNSdWU4RbTd1ZCTSQ0avqlkBHqOkTTMOPOsSHRvfaSGH05+tB1jU7wGPTtHniY/8ALa9IjRffaCWP0/Wnf8JhoX/QSh/I/wCFH/CYaF/0EofyP+FZfVq38j+5j5kWdJ0hdNWWWWVrm9uCGnuHGC5HQAdlHYdqp+M/+RWuvqn/AKGKf/wmGhf9BKH8j/hWfq2qQ+JYV0zSd06yupmnCkJGgIJ5PfitaFCpCrGcotJNNtoTaaP/2Q==[/img] ou en saisissant « cercle(H,r) »[br][/*][*]Placer un point libre, nommé A, sur ce cercle [br][/*][*]Tracer la droite (HA)[br][/*][*]Tracer la droite perpendiculaire à (HA) et passant par H[br][/*][*]Placer les points d’intersection, dans l’ordre anti-horaire B, C et D, entre les droites et le cercle[br][/*][*]Désafficher les droites et le cercle (clic droit « Afficher l’objet » ou clic sur le bouton [img width=13,height=13]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAA0AAAANCAYAAABy6+R8AAABx0lEQVQoU3VSMUtbYRQ9X96LoBliFoVky4MEVGwgHSxoFF3iEqgkGBwsgnUq7ZAq3SodxVEJbtF/oCiIg0nqs3YywWTQyUegUSFu5oW895Kv3302HVpzxu+755x77r2MC+APLgtF5HJ5lMtlNI0m+nr7EAqFMDkZwcjwUKcMjEhPT3VkdvdQKBTg9/sxODgA2emE0WyiWr1DpVJBRBAXkkn09DjBLMviW9tpaJqG0VejcDgcaLdaoAYYY5BkGaZhCMEiwq/DWHq3CKae/+CZzC7GJ8bRsiy7+F+QEL2r6jlSn1NgX9e/cZfLhQHRkmWa/xE6D9SudqvB4/GAzScXeHQ2+relbixyE1FwcfET7O1cnCcScei63tWFPigfuR0dHoHFE/M8FovBNI0X83SU7AG128jnv4Otrn3hPp8P7n63PYhuIJfqr6rtyI6PT/j+wQHG3ozZo30JVOiQJKhnKlZW3oPVdZ1vbGzaIQPBAFpiR7SnTg4qJlLpqgSv14tPHz88X8T9wwPS6R3UajUEg0F7rLIswRRCj7VHXN9cQ/ErwmUZ/W73M4lU9UYD2dMcTrNZ+2wotCyuQVEUzExPY2oqAkm4En4DazjMXbPlGhwAAAAASUVORK5CYII=[/img] colonne de gauche)[br][/*][/list] Il ne reste que les 5 points A, B, C, D et H[/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARMAAAERCAYAAABYYUOzAAAWEUlEQVR4Xu3deXSUVZ7G8ScbARKSAGGTHZEoizIKqOwogs4ojggKoyienlFQgbiwuDTSIoTFBQXFXaBFXFBbUVob7eNyzoB4xi2ANILI0qwJEDD7NreKgdZpkCK5Re5Nfd9z/ENTdd/f/fzueax637feN6rcbGJDAAEEKikQRZhUUpC3h0UgNzdPW7dv08+Hflbg/3exsbFq3bqV6qakhGV/DFp5AcKk8oaMEAaBtd+v17SHpqlhw4ZKSkrSwYMHlZCQoJtuGqm2p7cJwx4ZsrIChEllBXl/WAS+/S5TCxcu0qRJE9SwQYPgPqZNn6HmLZrrhuuvC8s+GbRyAoRJ5fx4d5gE1qxdp6effkZXDhqkevXraf++/frvlSs1aNAV6nzO2WHaK8NWRoAwqYwe7w2bwLr16zVr5mzVq1cv+DUnOzs7eOzklltuVqeOHcK2XwauuABhUnE73hlGge8y12jBgoVKTx+rFs2bq7ikRItfWaItP23RpIkTFB9fI4x7Z+iKCBAmFVHjPWEXCITJokV/1D33TFR98+kksC1f/oE++/xzTZ58v2rXqhX2GtjByQkQJifnxatPkUAgTGbMmKl+/fqqfv36ysvL10pzzKR3714aOnSIoqOiTlEl7CZUAcIkVCled0oFdu3erQ8+/IsO7D+gmJiY4L7T2rVTr949VatmzVNaCzsLTYAwCc2JVyGAwAkECBOWSJULHDJXuebm5apOYh1zYVrtKq+HAiomQJhUzI13WRDYt3+/OWOzSEuXvqF95tRvw0aNNGLECF1vLkrjq4wF4FM8BGFyisHZ3WGBwG9vJk66R4sXL1bLFi2UkJigQ+aS+a3btuvuu+/W+Lvv4vSvZ4uFMPGsYdWl3D/96V3ddecdamquIUlISFR5WZmiY2O0LytLWXv3asHCherZs0d1mW5EzIMwiYg2uzfJ++6frKWvv6ZWrdsEr2z95fbjpo1Kv/Mu3X7baPcKp6LjChAmLI4qETgSJq3bnK4y86nkl9vmHzdpbPodGnP7rVVSGzutmABhUjE33lVJgTeWvqWJ48ebrznNlGjO4pSVliomLtZcV7Jfe801Ji+8+JK5QK1nJffC20+lAGFyKrXZ11GBHHOwdcLESXrtVfNVp2VLJdZJNAdgD2nL1q3mx3y3aMqUyZzR8Wy9ECaeNaw6lXsgJ0fPPPOc3n77LeWbszt1kpN0zTXX6qaRN6qOCRc2vwQIE7/6VS2rDVy0tsecwWnSpDE/4PO4w4SJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAoSJx82jdARcEiBMXOoGtSDgsQBh4nHzKB0BlwQIE5e6QS0IeCxAmHjcPEpHwCUBwsSlblALAh4LECYeN4/SEXBJgDBxqRvUgoDHAtbDpKioWFnZWYqOjlbjRo08pqF0BBA4GQGrYfLV19/ogw8+VFRUlAoKClS7dm0NH36tWjRvfjI18VoEEPBQwFqYZK5Zq/nzn9aQq6/W+ed3U0FhgV58cYFycnJ0z6SJSkio7SEPJSOAQKgC1sLkqfnPqLCwUHekjz2673379+uHHzaqQ/v2SkxMCLUmXocAAh4KWAmTsvJyTZuWofbtz9LVg6/ykIGSEUCgsgLWwmT69BlKS0vT0CGDj9YUCJlt27YptX4qX3Mq2ynej4DjAlbCJDDHxa8s0aZNP2ry7+87OuVvv8vUCy+8qPHj71LzZs0cp6A8BBCojIC1MNmxc6cefXSOOp3dSd27X6icAzl6xQTMOZ3P0Yjrr1O0OcPDhgAC1VfAWpgEiLZt36733luu/ebAa0lJic45+2xdfvm/KiYmpvoKMjMEEAgKWA0TTBFAIHIFCJPI7T0zR8CqQIXCJHvfPiUlJSkuNtZqMQyGAAL+CpxUmPz1r5/oueefN6d7t6pOnSQNGDBAI0feoLopKf4KUDkCCFgRCDlMXnv9DaWPG6ea8fFKbdAgeLXr5i1bddmll+rZZ59WSnKylYIYBAEE/BQIKUw2/bjZXIw21JyhKVazFi1UVlKqqOgoFZtfCP/PV19pzuNzdOOI6/0UoGoEELAiEFKYBE733nbraJ3RLi14mrfcXNka2GLMMZNNP2xQn34X6amn5nEMxUpLGAQBPwVCCpM333pbd5ivOGlnnhW8T8kvw+SnzT/qvK5d9aI5llKjRpyfClSNAAKVFggpTNZ+v15DBg9WsjkuUrdefZWVmq855orWQKh8sXq1pkyZYo6njKl0MQyAAAL+CoQUJoHpzZg5W9OmT1fbNm2UUjdFxcXFWr9+vTp06KBXX12iJo0b+6tA5QggUGmBkMOk1Hwamf/0s1rw0kvauWOHuYtaLXXv2Uv33nuP0tqdUelCGAABBPwWCDlMjkxzz9692r17T/CWjKe3ae337KkeAQSsCZx0mFjbMwMhgEC1EiBMqlU7mQwCVSdAmFSdPXtGoFoJECbVqp1MBoGqEyBMqs6ePSNQrQQIk2rVTiaDQNUJECZVZ+/VnouKpGXvFqhtu1hzO87D97E5eLBcf15eaH5OEae2p3NrTq8aGoZiCZMwoFbHIfMLzLORHsxXz14xuvSy+OAU9+4t08yMAg25Jk4XXMDvsqpj309mToTJyWhF8GsDYfLI7Hz17h2r3n1qBCV+/rlcs2fl64pBcerShTCJ4OURnDphEukrIMT5B77mzMjI06GDUtNmhx9bUlhYro0bynXb2Brq3JkwCZGy2r6MMKm2rbU7MXNjPc2amad69aLUvkPgnjZSXm65PlpRohtG1tC55xImdsX9G40w8a9nVVLxsb7m5JowmTWTrzlV0hAHd0qYONgUF0sKhMlsExzdu8eq/yWHj5lkZZVpzqMFuvKqOHU1Z3TYIluAMIns/oc8+yOfTC68MFYX9/9HmDwxp0CD/p0DsCFDVuMXEibVuLk2p1ZmjpEETgXXrhVlHnNy+ABscYmUnV2mOolRSkjgWdI2vX0cizDxsWvUjICDAoSJg02hJAR8FCBMfOxamGves3entm/fah4Bm2wuk29n9hYd5j0yfHUQIEyqQxctzWHX7h2aO3euPv7oax3YL8XVKNXpbZN1R/po9elzsaW9MEx1FSBMqmtnT3JeW7f9pN/9bpw2rGutNq1vMI81aWGucC0wn1BW6FDuAmXMGqXhw4af5Ki8PJIECJNI6vZx5lpkrpWfdM99WvZ2nPlF8H0yD2pUWZn5rYU5QWMe4KjNm1equPxRvbQgQ506noMYAscUIExYGPp+faZuGPEHJSc8qNTUljJPNfnVFgiVb76dqvTxTXXrKB62xpI5tgBhwsrQ+++/o/vvW66WzTLMI17jg7+7+eUW+HTyw8al6tEnU489mmE+rXC1K8vmnwUIE1aFPvlkhe68c4maNpqhWrUSjhkm6/+2SP925Q5NnfoHRUdxdodlQ5iwBo4hsHPXdg0bNlZFuaPUqlUPlZgrW49s5jn15kBsvr5bk66ZD1+uoUOGYYgAx0xYA8cXeHnxIt076XWd0SZDjRq1OfrCoqJSffXVY+rWY7PmzZut1PoNYESAMGENHF+guKRYc+Y8pvnz3ldczEClpJypgoKD2rP3PXXrHmUeWv+AOrbvCCECxxXgmAmL41cCK1d9rhUrPtCaNRtVPzVZvXr20JWDBpsf8tVBCoHfFCBMWCAIIGBFgDCxwsggCCBAmLAGEEDAigBhYoWRQRBAgDBhDSCAgBUBwsQKI4MgUH0E8vLLg48xSU6JVtzhJ8GGtBEmITHxIgQiR+CzT4u0alWJeepADaWZZ0uHuhEmoUrxOgQiQODQoXItf78w+OjX006L1oCB8cHbUISyESahKPEaBCJEYO26Eq3NLFG7tBhlZpYGH2tyWpPQfthJmETIImGaCJxIIPA4kz+bTyVJSVHq1buG3n2n0NxxL0p9+h5+TtKJNsLkREL8HYEIEdhjnov0ztuF5oee0WreIlrr1pUGf0F+9dXxSjTPRjrRRpicSIi/IxAhAl9+WaxVK0vUtGl08JadxSXl2rWzXJcMjNNZZ574QCxhEiELhWki8FsCgYfQL11aqJYto9X3/77WBL72LHu3UAXmVPFVg2uau/D9tiFhwhpDAAFzq4kyZX5Xog4dY9XYfM05sv20pVQbN5Tq3PNiVa/ebx+IJUxYSAggYEWAMLHCyCAIIECYsAYQQMCKAGFihZFBEPBHIHtflrmv75f624b1apDaQJ07dzGXzZ9Z6QkQJpUmZAAE/BH46OMVysh4XDv/Hmfu83uWCosOKD9/jYb/R3+NHTtWyUkpFZ4MYVJhOt6IgF8Cn3/+mW677X61ajla3bpdofj46ODTG3ft2mzu+zvN/LCvlR6YPNn895oVmhhhUiE23oSAXwJ79uzWbbePV+6hPurXb7iKi//xPOnA9SO7d+/Rxx+na8bM0Ro4cGCFJkeYVIiNNyHgl8AXq1dpwvh56tZ1muqbZx/98kFrgatdA/98/PGT6j+gTBMnTjBPbTzx5fP/X4Aw8WtNUC0CFRL48MMP9cADS9X/4odUu3YdlZX9ephYc7X86tXvqFmLLzV71vQKfdUhTCrUGt6EgF8Cq79cpbvvnqtuXaYpNbXhP30yCTwGdsWKJzXg0nJNmjjeTI5PJn51mGoROEUC+/Zna8zYCTqQ3dMcMxmmoqLyo59O4uOlnTt36NNPJ2jGrFG6pP+AClXFJ5MKsfEmBPwT+OyzTzVu7FQ1b/6f6tLlCtWsGaVy82O+bVs3acVHD+ja4Z3M2ZzfmzurnfgXwseaPWHi35qgYgQqLLDio79o1swntHNHjOLimplPJwdVrq267vrLNGrUaHOdSXKFxyZMKkzHGxHwU+BAzj59uXq1Nm/ZasKjjjp26qgOZ3Wq9GQIk0oTMgACCAQECBPWAQIIWBEgTKwwMggCCBAmrAEEELAiQJhYYWQQBBAgTFgDCCBgRYAwscLIIAggQJiwBhBAwIoAYWKFkUEQQIAwYQ0ggIAVAcLECiODIIAAYcIaQAABKwKEiRVGBkEAAcKENYAAAlYECBMrjAyCAAKECWsAAQSsCBAmVhgZBAEECBPWAAIIWBEgTKwwMggCCBAmrAEEELAiQJhYYWQQBBAgTFgDCCBgRYAwscLIIAggQJiwBhBAwIoAYWKFkUEQQIAwYQ0ggIAVAcLECiODIIAAYcIaQAABKwKEiRVGBkEAAcKENYAAAlYECBMrjAyCAAKECWsAAQSsCBAmVhgZBAEECBPWAAIIWBEgTKwwMggCCBAmrAEEELAiQJhYYWQQBBAgTFgDCCBgRYAwscLIIAggQJiwBhBAwIoAYWKFkUEQQIAwYQ0ggIAVAcLECiODIIAAYcIaQAABKwKEiRVGBkEAAcKENYAAAlYECBMrjAyCAAKECWsAAQSsCBAmVhgZBAEECBPWAAIIWBEgTKwwMggCCBAmrAEEELAiQJhYYWQQBBAgTFgDCCBgRYAwscLIIAggQJiwBhBAwIoAYWKFkUEQQIAwYQ0ggIAVAcLECiODIIAAYcIaQAABKwKEiRVGBkEAAcKENYAAAlYECBMrjAyCAAKECWsAAQSsCBAmVhgZBAEECBPWAAIIWBEgTKwwMggCCBAmrAEEELAiQJhYYWQQBBAgTFgDCCBgRYAwscLIIAggQJiwBhBAwIoAYWKF8dQPUlxSos8+/Vw/bNyoqCipvFxq3KiR+vbro5Tk5FNfEHuMeAHCxNMlkJefr4yMmYqPj1fbtqeroLBQ69auU7IJkltvHaW6KSmezoyyfRUgTDztXG5unubOe1IDBw7Qv3Q+JziLAzk5euih6erRvbuuuupKT2dG2b4KECaedu5ImPTt20cXnN/t6Cyefe555eXlK33cGE9nRtm+ChAmnnbueGHy0oKFysk5SJh42lefyyZMPO3ekTC56KJ+6ta1y9FZPPnU04qOjtboUTd7OjPK9lWAMPG0c4EweWLuPAXC5PxuXYOzWPv9es1/ar6GDbtWPXt093RmlO2rAGHiaefyCwo0a9bD2r17txo3bqwC8+9Z2Vnq26ePhg4dorjYWE9nRtm+ChAmnnauzFxYsnnzT8EwKSsrM9eaRKlBwwZq17atpzOibN8FCBPfO0j9CDgiQJg40gjKQMB3AcLEgw5+8+13+vrrrxVlztJ0Oe88dezQ3oOqKTHSBAgThzseuKI1cJD15UULf1XlmHHpGjvmdnMpfQ2Hq6e0SBMgTBzu+JzH55rL46cqLS1NSUlJwUr3ZWdrww8b9cgjD2vkyBsVHfiVHxsCDggQJg404Vgl7M3KMqd4r1HOgRw1btJEpeZXwoEttkactm3ZoqZNm+mPLy9Sg9RUR2dAWZEmQJg42vGvvv5GN//XzYqvGa/EhERziwFzjwGzBa5uPXBgvwoLi/TmW2+qTetWjs6AsiJNgDBxtON/37FDQ4YMVXFRcfD6kdKS0mClMeZitJ3mb3Xr1dWSJa8E72HChoALAoSJC104Tg0PTHnQXB7/pNp36KDaCQnBV+Xl5iozM1MTJ07SXXemKyYmxuEZUFokCRAmDnc7yxxsHT9+ot5/b5lq1awZ/Kpz8OdcDR8+TFOnPqjU+vUdrp7SIk2AMHG840Xma867y5bpiy9WBy+Z79Wzpy69bCC/vXG8b5FYHmESiV1nzgiEQYAwCQMqQyIQiQKESSR2nTkjEAYBwiQMqAyJQCQKECaR2HXmjEAYBAiTMKAyJAKRKECYRGLXmTMCYRAgTMKAypAIRKIAYRKJXWfOCIRBgDAJAypDIhCJAoRJJHadOSMQBoH/Bc4rpEZIFQTZAAAAAElFTkSuQmCC[/img][/td][/tr][/table]