9. Klasse Mathematik
9. Klasse Mathematik
Table of Contents
- Quadratwurzeln
- M9 - Quadratwurzeln bestimmen
- M9 - Quadratwurzeln geometrisch darstellen
- M9 - Heron-Algorithmus
- Quadratische Funktionen
- M9 - Quadratische Funktionen entdecken
- M9 - Parameter des allgemeinen quadratischen Funktionsterms erkennen
- M9 - Quadratische Gleichungen grafisch lösen (Stufe 1)
- M9 - Quadratische Ergänzung - Einführung
- M9 - Quadratische Ergänzung - Übung
- M9 - Scheitelpunkt mithilfe des Funktionsterms angeben
- M9 - Funktionsterm zur verschobenen Normalparabel angeben
- M9 - Quadratische Gleichungen grafisch lösen (Stufe 2)
- M9 - Funktionsterm zu beliebiger Parabel angeben
- M9 - Zuordnung einer Parabel zum Term in Scheitelpunktform
- Ähnlichkeit und Strahlensatz
- M9 - Strahlensatz bei der V-Figur - Einführung
- Potenzfunktionen
- M9 - Eigenschaften von Potenzfunktionen untersuchen
- Satz des Pythagoras
- M9 - Satz des Pythagoras beweisen - Arbeitsauftrag
- Trigonometrie
- M9 - Sinus und Kosinus am Einheitskreis
- M9 - Sinussatz - Herleitung
M9 - Quadratwurzeln bestimmen
M9 - Quadratische Funktionen entdecken
Vervollständige zum gegebenen Funktionsterm die Wertetabelle.[br]Hast du einen Funktionswert richtig in die Tabelle eingetragen, so wird der zugehörige Punkt des Funktionsgraphen im unteren Fenster eingeblendet.[br][br]Hast du alle Funktionswerte richtig eingetragen, wird der komplette Funktionsgraph eingeblendet und du kannst eine neue Aufgabe generieren lassen.[br][br][color=#0000ff][b]Sammle mindestens 5 Punkte![/b][/color]
Untersuche, welche Struktur alle Funktionsterme in der ersten Aufgabe hatten, und beschreibe diese.[br]Kannst du einen allgemeinen Funktionsterm mit Parametern angeben?
[b]Bonusaufgabe:[/b][br]Vielleicht hast du erkannt, dass die zweite Hälfte der Wertetabelle leicht auszufüllen war.[br]Das war nur möglich, weil die vorgegebenen x-Koordinaten in der Wertetabelle geschickt gewählt wurden.[br][br]Versuche zu erklären, aufgrund welcher Eigenschaft der betrachteten Funktionen der zweite Teil der Wertetabelle leicht auszufüllen war und wie dafür die vorgegebenen x-Koordinaten gewählt wurden.
Die oben betrachteten Funktionen werden [color=#6aa84f][b]quadratische Funktionen[/b] [/color]genannt.[br][br]Gib in den unteren Fenstern drei verschiedene Terme quadratischer Funktionen an und vergleiche deren Funktionsgraphen miteinander.
M9 - Strahlensatz bei der V-Figur - Einführung
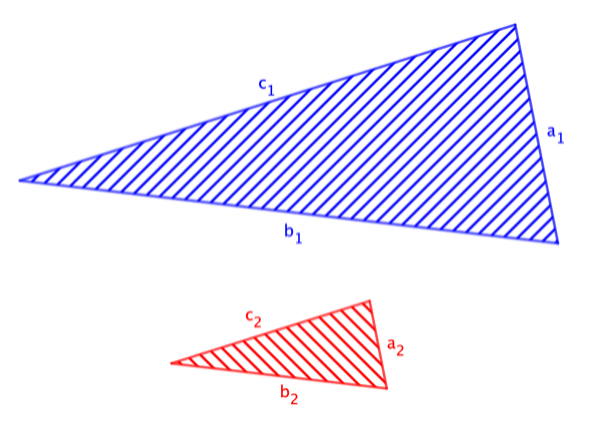
Die beiden unten dargestellten Dreiecke sind [b]ähnlich[/b] zueinander. Ihren Ähnlichkeitsfaktor kannst du mit dem Schieberegler anpassen.[br][br][b][size=150]Gib die Zahlenwerte zu den gesuchten Längenverhältnissen in die Eingabefelder ein.[/size][/b][br][br]Hast du das richtig gemacht, kannst du eine Animation starten, welche die beiden Dreiecke verschiebt.[br][br]Die Darstellung, die du dann erhältst, hilft dir dabei, die nächsten Aufgaben zu bearbeiten.
Die beiden im folgenden dargestellten Dreiecke sind ähnlich zueinander.
Kreuze an, welche Gleichungen richtig sind.
Gib weitere gültige Gleichungen an, die sich auf die Seitenverhältnisse in den oben dargestellten Dreiecken beziehen.
Kreuze an, welche Gleichungen richtig sind.
Gib weitere gültige Gleichungen an, die sich auf die Seitenverhältnisse in den oben dargestellten Dreiecken beziehen.
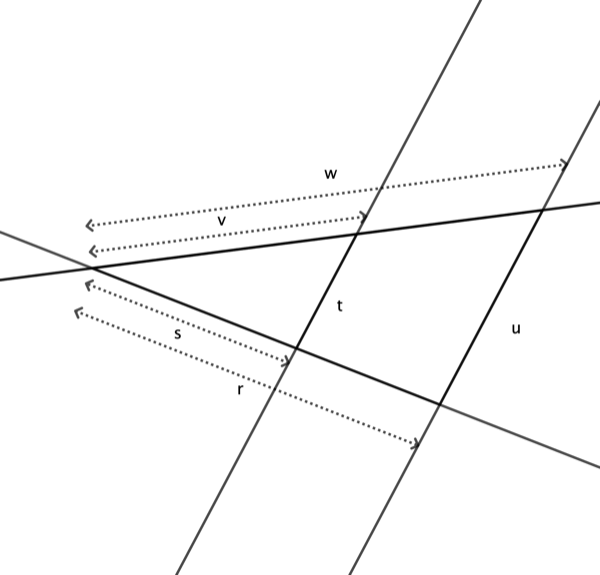
Gib gültige Gleichungen an, die sich auf die Seitenverhältnisse in der oben dargestellten Figur beziehen.
M9 - Eigenschaften von Potenzfunktionen untersuchen
Auftrag 1
Untersuche Funktionen des Typs [math]f:x\mapsto x^n[/math] mit [math]n\in\text{ℕ}[/math].[br]Dazu kannst du mit dem Schieberegler in der linken Grafik die Zahl [math]n[/math] verändern.[br][br]Beobachte dabei den Graphen der Funktion [math]f[/math] und ziehe dann die Kärtchen auf der rechten Seite[br]mithilfe der Punkte an die richtigen Positionen.[br][br]Wenn du alle Kärtchen an die richtige Position gezogen hast, erscheint die nächste Aufgabe.
Auftrag 2
Nun sollst du Funktionen mit dem Funktionsterm [math]f\left(x\right)=a\cdot x^n[/math] mithilfe der Schieberegler untersuchen.[br][br]Fasse dann deine Beobachtungen ähnlich wie in Auftrag 1 auf einem Schmierzettel zusammen.
M9 - Satz des Pythagoras beweisen - Arbeitsauftrag
Erarbeitet mithilfe des unten dargestellten Applets eine Präsentation für den Beweis des Satzes des Pythagoras, die auch für ein Lernvideo abgefilmt werden könnte.[br][br]Zum Satz des Pythagoras gibt es unzählige Beweise. Ein paar davon werden im unten dargestellten Video gezeigt.[br][br]Derjenige Beweis, den ihr mithilfe des Applets demonstrieren sollt, ist im Video bis zum Zeitstempel 3:47 gezeigt.[br][br]Hier könnt ihr euch also Hilfestellung holen.
[b][size=150][u][size=200]Für Interessierte[/size][/u][/size][/b]