DISTÂNCIA ENTRE DOIS PONTOS
Mude os valores de x[sub]1 [/sub]e x[sub]2 [/sub] para 3 e 8, respectivamente, e observe o que acontece com a solução. Por que isso ocorre?
Se mudarmos os valores de Y[sub]A [/sub]e Y[sub]B[/sub] para -3 e 5 respectivamente. Qual será o novo valor da solução? Mostre algebricamente como você chegou neste resultado.
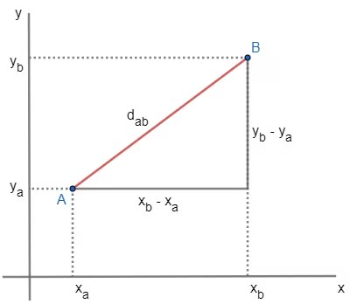
[justify]A distância entre dois pontos depende do lugar geométrico em que esses pontos estão localizados. Por exemplo, se dois pontos estão em uma reta, a distância é dada pelo módulo da diferença entre eles.[br][br]Para determinar a distância entre dois pontos no plano cartesiano, é necessário realizar a análise tanto no sentido do eixo das abscissas (x) quanto no do eixo das ordenadas (y). Confira:[/justify]

Note que na distância entre o ponto A e B existe uma variação tanto no eixo x quanto no eixo y, logo, a distância entre os pontos deve ser dada em função dessas variações.
A distância entre os pontos A(x[sub]a[/sub], y[sub]a[/sub]) e B(x[sub]b[/sub], y[sub]b[/sub]) é definida pelo comprimento do segmento representado por d[sub]ab[/sub]. Mostre de forma generalizada como encontrar esta medida.
AGORA É SUA VEZ
[justify]No software Geogebra, disponibilizado acima, plote seis pontos (A - B - C - D - E e F respectivamente) na janela de visualização utilizando o segundo item da barra de ferramentas à esquerda no canto superior. [br][br]Em seguida ligue os pontos A e B - C e D - E e F formando os segmentos AB - CD e EF. Para isso clique no terceiro item da barra de ferramentas e selecione a opção segmento.[/justify] [br][br]
Qual a distância entre os pontos A e B? Entre C e D? E a distância entre E e F? Mostre como você chegou nesses resultados.