IM Geo.3.4 Lesson: Dilating Lines and Angles
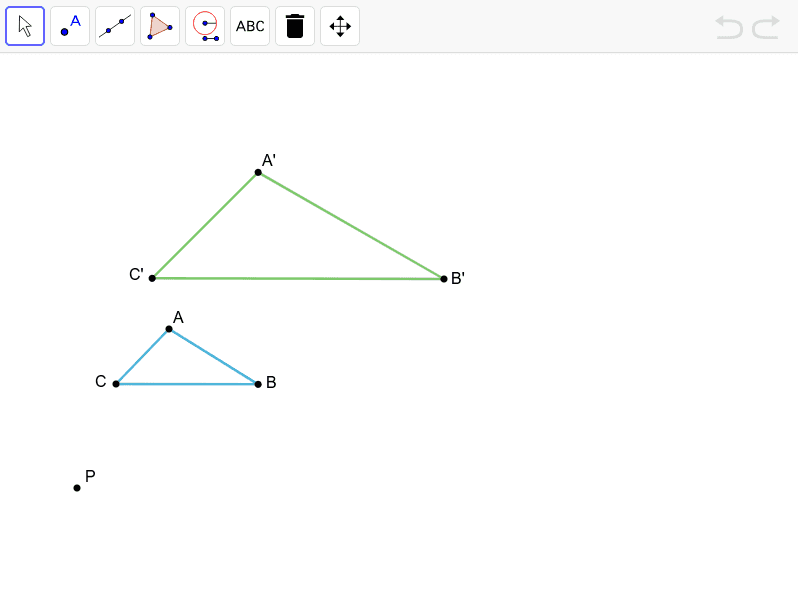
Triangle A'B'C' is a dilation of triangle ABC using center P and scale factor 2.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUYAAAEhCAYAAAADJgkSAAAgAElEQVR4Ae2dCXRURbrHg8tTFCf4HuN7Z8ZneGfe8JxFg+M2uEyiKAIiQVQ20aC4IwYUcEFMRAVUIMi+aQDZBQIhEMLWSSBAEshCFpKwhEDYISEkhLB+73yVvqG7s93uvmvff53znb5L3Vp+VfffdW/dqvIjOBAAARAAAScCfk572AEBEAABECAIIyoBCIAACLgQgDC6AMEuCIAACEAYUQdAAARAwIUAhNEFCHZBAARAAMKIOgACIAACLgQgjC5AsAsCIAACEEbUARAAARBwIQBhdAGCXRAAARCAMKIOgAAIgIALAQijCxDsggAIgACEEXUABEAABFwIQBhdgGAXBEAABCCMqAMgAAIg4EIAwugCBLsgAAIgAGFEHQABEAABFwIQRhcg2AUBEAABCCPqgCkJhISEkM1mM2XakWjjE4AwGr+MLJ3CsLAwCg4OdmJQVFREfn5+xL9wIKAGAQijGlQRpiIEuEXo7+8vRNAxwMjISOIWIxwIqEUAwqgWWYTrNYGgoCAKDw8Xwuj42MzHHfe9jggBgIALAQijCxDsGoNAVFSUaC2WlZU5CSPvBwQEGCORSIXPEoAw+mzRmjtjLH7cWmTnuB0dHU0smnAgoCYBCKOadBG2RwT4HSK/W+TWITvpkZq3pWMeBYyLQEAmAQijTFDwpg0BFr6WLVvWthY5Vu5oYXGEAwGtCEAYtSKNeGQRkDpb+HMcR4MwysIHTwoRgDAqBBLBeE+Av0uUWovc6yxZaGhonU92vI8NIYBAwwQgjA2zwRmNCbAA1tfjzALJrUc4ENCKAGqbVqQRT6MEpNEs9fU4S8LIv3AgoAUBCKMWlBFHkwT4HWJ9rUXpQm4xQhglGvhVmwCEUW3CCB8EQMB0BCCMpisyJBgEQEBtAhBGtQkjfBAAAdMRgDCarsjMm+Ann3ySbrzxRmrWrBkFBgaaNyNIuc8TgDD6fBEbI4OdOnVy+mCbO1MgjsYoG6SiLgEIY10mOKICgdtvv72OMHLLEQ4EjEgAwmjEUvHBNN1xxx11hPHmFjdRafUpH8wtsmR2AhBGs5egSdIfFPpoHWFs/Uor6r72cVq2b65JcoFkWoUAhNEqJa1jPn/Om0DtV/6VHuv3ALVo0YKaN29OHTp0oKzTafTF9vfFuQGJvSj52GYdU4moQeA6AQjjdRbYUoHA7LxIIXwTMr9uMPT1h1bSm5u6Cn/fpg2hovLCBv3iBAhoQQDCqAVli8YxK3d8jShmjWySwMUr1TQvfwp1Xv0PcQ23MquvXGjyOngAATUIQBjVoIowaWbuWCFwP8kQRUdcxef20w/pX4hr+254juKKlzuexjYIaEIAwqgJZmtFMiPnR7sofuNxxlOOJ9HHW0NFOEOT+1PmqRSPw8KFIOAuAQiju8Tgv1EC07J/EGI2MctzUXSMYNWBRdRn/TMizPGZ4XSi6qjjaWyDgCoEIIyqYLVmoFOzx9hF8VtFAZRfLKMZOTWP5l1iH6LFhbMVDR+BgYArAQijKxHse0RgSvZoIYqTdn/n0fVyLiooy6GRqYNFPO/YulPikXVyLoMfEHCbAITRbWS4wJXA5N2jVBdFxzgTj8TTBwk9RJwRKWFUWJbreBrbIOA1AQij1witHcCk3d8KgWJx1Not2fsLvbj2MRE/d/hUXCrXOgmIz0cJQBh9tGC1yBZ3sPCIFj1EUcrf8fNH6Cd7OnqsC6aYokXSKfyCgMcEIIweo7P2hROyRgpRnLJ7tCFAZJ1Kpc+3vyfSNHjL65R2Yqsh0oVEmJMAhNGc5aZrqiMzI2pEMdsYougII744mt7Y1EWkjz8UL6k86Hga2yAgiwCEURYmeJIIjM8IF6LDn+YY1fFQwrl7JlPHmEB6dtXf6df8qXT12lWjJhfpMiABCKMBC8WoSRqX8ZXhRdGR3cFz++j7XZ+LNL+x8XnaeHi142lsg0CDBCCMDaLBCUcCYzO+FAIzLft7x8Om2N5xPJH4vSN3FA3f/j7lnskwRbqRSP0IQBj1Y2+amH9IH25aUXSEvPLAQuoV/7TIC/ekl1afdjyNbRCoJQBhrEWBjfoIfG+f6WZ6zg/1nTbdsbMXS0ma5CJkzT9p+f55pssDEqw+AQij+oxNG8OYXZ+J1tX0nB9Nm4eGEp5flk1fpw4S+RuQ2JO2YfbwhlBZ8jiE0ZLF3nSmR+/6VIgGt6582SUcWUfvJbws8vrdzqFUdG6vL2cXeZNJAMIoE5SVvI3aOdQuimMtk+3Fe3+mkDWPinz/kvcTZg+3TMnXn1EIY/1cLHuU11zh3tuZOdYRRamwj58vIWlET+/49hRXvEI6hV+LEYAwWqzAG8vuN2mf1Ihi7rjGvPn8OZ4t/LNt7wgWNbOHp/p8npFBZwIQRmcelt0bmVYzz+Esi4uiYwVYV7yCQjd2EgLJwyAxe7gjHd/ehjD6dvnKyp3UO8ur+sE5E7hwpYrm7JkkhhbyEMPFhT87e8CeTxKAMPpkscrPVERqmGgRzYYoNgqNe6ulz5f6bw4hniwXzncJQBh9t2ybzNlXKQPtohjZpF94qCGw/XgChSX1FdzCUz6iwrOYPdwX6waE0RdLVUaeRqR8KG5uXtgezn0CKw8soFfWBQmGvFBXxaVz7geCKwxLAMJo2KJRL2Ff7hgAUVQAb1n1GeKhkvx5U/e1j1NM0WIFQkUQRiAAYTRCKWiYBp5dhm9k/ogZThkCe0p3Ez9WM9ePkvpQ2olkZQJGKLoRgDDqhl77iL+wT/0PUVSHva0kjt7e/KIQSJ58o6SyWJ2IEKrqBCCMqiM2RgSfb3/X3lKcaIwE+WwqrtGiwtnUJfYhwfvX/Gl0DbOHm660IYymKzL3E/zptrfFTRq1B6LoPj3Prjh2/jBJa+P03dCBNh6O9SwgXKULAQijLti1i3RY8lt2UZykXaSIqZZAxqkdNCy5vygDHmaYV5pZew4bxiUAYTRu2XidMh7nyx0CPHIDTl8CccXLiVuOXB6Td39HZZg9XN8CaSJ2CGMTgMx6ekjyG3ZRnGzWLPhcuqsunyd+ncHi+PzqB2n5/l99Lo++kiEIo6+UpEM+PtnaT9x8vIQonPEIHCgvpFE7h4kyesfWnbYfsxkvkRZPEYTRxyrA4C2hNaKYP8XHcuZ72WFB/DCxtygvnt2Il3uFMwYBCKMxykGRVAza8pq4yeblT1UkPASiDYHo/fPppbgnRNnxN6YXr1RrEzFiaZAAhLFBNOY6EbalZmID/m4OznwEeCnXqdljhDi+Evcv4rkg4fQjAGHUj71iMX+U9Kq4oeYXTFcsTASkD4G80iySxrIP3vI6ZZ1O0ychFo8VwmjyCjDQ/o4KomjygnRJ/uaStdR/U1fxhzc2YwSdrDrm4gO7ahKAMKpJV+WwByT2EjfOgoIZKseE4PUgwEMJFxbOpE6rHxDljNnDtSsFCKN2rBWN6YOEHuJm4RsHzrcJHK08ROMyRojyDt3YmZKOrPftDBsgdxBGAxSCu0l4P+EVcZMsKpzl7qXwb2IC6Se3k/SNKk8ft/dsnolzY+ykQxiNXT51Uvee7WX7Y9XsOudwwBoE1h5cRrzuNY+gmZb9PVVeqrBGxjXMJYRRQ9jeRvWurbu4GZbsxUp13rI0+/XnL1cSL0vB4vhC7COYPVzhAoUwKgxUreDesdVMgLpk7y9qRYFwTUjgQHkBfZP2iRBIfsWy8yRmD1eiGCGMSlBUOYy3NncTFX/p3iiVY0LwZiWw7dhmkjrkvts5lI5UHjJrVgyRbgijIYqh4URI37L9tm9Ow55wBgTsBJbvm0fd1rQTf6Q8icg1ugY2HhCAMHoATatL3tz0gqjgy/bN1SpKxOMDBM5Un6JJu78TdadX/FO0CbOHu12qEEa3kWlzwRsbu4iKzS0AOBDwhEDumUySFkD7ZOsbxMMN4eQRgDDK46Spr34bO9eI4n6IoqbgfTQybjH22/i8qFO8Dg2vhw3XOAEIY+N8ND/7+sZOogKvwOzOmrP35QivXrtKvxZMo+di7qcOq+4jvLNuvLQhjI3z0fTsaxs6ClHk+fngQEANAkcqi+mH9C9EPeN32Jg9vH7KEMb6uWh+VFooaeWBBZrHjQitR2DXyW0kTWz8VcqHmD3cpQpAGF2A6LH76vpnxT/4qgML9YgecVqYQGzRUuq5LljUvxk5Y+ni1YsWpnE96xDG6yx02eoT/4xdFBfpEj8iBYHzlytoZu44UQ+7rW1Haw7+ZnkoEMZ6qkBkZCSFhITUc0bZQ73inxaVMaZosbIBIzQQ8IDA/vJ8ikgdJOokL9LlC7OHR0V5NlrMksJYVFRE/fr1Iz8/v1pr3bo1RUdHi+oUGBhI4eHhHlQt+Zf0XPeUqICri5bIvwg+QUADAluPbqR3bS+J+jlm12d0suq4BrG6HwU3YCIiIoTNmTOHEhISnALh+5nvcU+cZ1d5EpNBrmFYLVu2pKCgICGELJI2m40YMm+XlZUJmPyrluthf6fD73fgQMCoBHhsPs/cwzP4zC8w3iJrLHrciOF7mX95nxs40r0bGhpKbJ44SwkjCx/DawwWN70bO+8JZMdreAU4rmh4j+NIBdtGJXD6wkn6KWukqLN91j9LtpI4QySVGzN8L2dkZNSmh7f9/f1rn/YCAgJEY6fWgxsblhJG/mdhWI05frfIAqqGeznuSbsoLlMjeIQJAqoRyDmTTp9ue1vU32Hb3tJ99nB+wmMRdHV8j/M9zCLJ2546ywij1Fps6mWsWp0u3e0Lqq89uNzTssJ1IKA7gfWHVtHr9oEIE7O+Je7R1sPxfeoqfPwIza/JWDTZpD4DT9JnGWFkUNz0lt4/eALL02teXPuY+KeNK4YoesoQ1xmHwJVrV4inNHtm5d+oU8wDpMfwVX7y4w5U7nBh404Yfr8ovQZrqgHUFE3LCCP3MtfX9G4KkLfnpbnx1hWv8DYoXA8ChiJQUnmQRu/6VPzpv725G6We2KJJ+rhxw40cqeOF72veHzRokGLxW0YY+Z/EtemtGMUGAgpZ86ioNPHFNZ8BNeANh0HA1ARYED9K6iPqOn8Hqfbs4VLHi+PTH78qY4EMCwtThKVlhJFbjPyvopXruqbmM4f4Qyu1ihLxgICuBFYdWERSB+PsvEjV0sL3cn2dqCyK/I5RCaedUiiRWi/CkD729Pbdg5wkvBD7sPj35BfVcCBgJQKVl87RtOwfRP1/Ke4JWqfC05LU8+zKtb4OGVc/cvctI4wMhIHyP8qECRNqX9ryNjfNlXLPr35QVIoNh2KUChLhgIDpCOw9m0dfpQwU90JYUl/iz32UcvzI7DoyTXq8dj3uaZyWEkZ+J8HNbW6G82M1G297063vCL7z6n+IirDx8GrHw9gGAcsSSDwST9Iqlz+mD6ezF0u9YiF9dte2bVsKDg4Wxtt8Lyv1fpETaClh9KpEmriYP1vgES1YeKgJUDhtSQKLC2eT9DS1qHCWxwxYGLlV6GjcWuTjSjoIowI0O8YE2kVxjQKhIQgQ8E0Cpy4cp/GZ4eJe4dnqk46sN2xGIYxeFs1zq+4XBb25ZK2XIeFyELAGAZ7ObEjym+K++Xz7u3SgvNBwGYcwulEkmzZtonvuuYduuOEGuvPOO+mBr1qLwjXKwHo3sgKvIKA7AR70IM1eP2X3aLp09aLoCO3cuTO1b9+eFi/Wb55SCKMb1aN58+a1nTZS5824ZaPcCAFeQQAEHAlcvnqJfsn7STQwHh31Z2p2w/U5UpXuUHGMt6ltCGNThOznJ0+eXEcUueDu7/0n4sXMh7Alv0lDhfWnocn9aVjyW8QzkfCsJGyfbXtHGD8+1Nh7YkH0L7a/T8PZdnxAXwobQCN2sH1II1I+FJ898KcP4SkfCYtIDSO2r1MH2W0wjUwdTCPTPqZvhH1C36axDaHvdrINpVHChtGoncPEMC4eysWTkLJ9v+tzYbx6XI0NJ+5B/DH9SxqbwTaCxgn7isZnfCXeE/G7Il6jmG1C5tc0IXOkmJ7qp6xvaKKwb4knGZi0+zthk3ePIjZuGUzJHk1Ts8fY7Xuals32A03PYfuRZggbSzNzxoop92fljqNZueOFzc6NJP54+Oe8CcL4pmKLyptIUXvYJtEcYZPFeN65+VNonrCp9Gs+2zSxjOj8gunEtqBghrCFBTNpYeFM4o6BGptN3GGweO/PtETYL7R0L1uUMF5+lG3ZvrnClu+bR8v3zxPjhnns8Ir984lXe4w+sIB4gbOVBxYSr+nDH0HHsBUtFsYTFbPx3JyxB5eK6eh4Sro1B5fRWmHLicfYxxWvIG5h8XeBPJKKBw6w8beybPx52IbDMcRfRLBxJ2CNraHNJWxrySYsjhJK4ijhyDph3GvMxu/72LYc3SCMJ6utsU2UfIxtM20TZhMrC24/nkA7hCXSjuOJlHI8SRiPgmFLO7FV2M4TybTzJNs24gW4dp3cTunCdlDGKbYUYZmnUuk/77uzzj122223ybxDlfUGYZTJc+LEiXUKjYXxvt5/osFbXncyXn3N0cK29CVhSX2Jv+kKS3qVPnKyPjQwydF608DE3sTTy9dYL/owscYGJPaiAYk9a+2DxJ70QUIPJ3s/4RVytPcSXqZas71M79leEjM08yzNNdad3rV1p3ec7EV6e7OjdSMeD8ufXtRYCL21OYT6S7apK/W325ubuhIvzelob2zqQrW2sYtYAJ4Xgb9unSl0o6N1Il5j+/UNknUUs7rwS/sae45e21BjfTc8R7zKYt/1Nfbq+g7iEY0f0yTrs/4ZcrTe8e3J2Z4mXmriuj1FveKfop5s69iChfEkw9ctiHqsC6JXau1fxPNtvlxrT4qRIDwa5CVhTxB/9CxZ97WPk6PxZCPO1o54DRZha9pRtzX/pBAne5R42GnXWnuEeMRV19hHxASzPNBAsi6xD1OX2IecjHuJHY0/N3O2B6jTarvFPECdYtpSRycLJO54fM7J7id+796h1u4T61g/u+o+qrG/07OrauyZVX8XE1HwZBRst/3x3+q9x2Teoop6gzC6gfPWW2+tU3CxsbFuhACvIAACDRG4995769xfrVq1asi7qschjG7gjYuLo7vvvlt0vtT39b0bQcErCICAC4GsrCxq0aJFrTjefPPNunXAQBhdCge7IAAC+hKYPn26GLarZyogjHrSR9wgAAKGJABhNGSxIFEgAAJ6EoAw6kkfcYMACBiSAITRkMWCRIEACOhJAMKoJ33EDQIgYEgCEEZDFgsSBQIgoCcBCKOe9BE3CICAIQlAGA1ZLEgUCICAngQgjHrSR9wgAAKGJABhNGSxIFEgAAJ6EoAw6kkfcYMACBiSAITRkMWCRIEACOhJAMKoJ33EDQIgYEgCEEZDFgsSBQIgoCcBCKOe9BE3CICAIQlAGA1ZLEgUCICAngQgjHrSR9wgAAKGJABhNGSxIFEgAAJ6EoAw6knfJW6bzUbBwcFi0XGXU9gFARDQkACEUUPYTUUVEBAgFgIKDw9vyivOgwAIqEgAwqgiXHeCjoqKIhbGoKAgCgsLc+dS+AUBEFCYAIRRYaCeBFdWVkatW7cmbimyKLI4woEACOhHAMKoH/vamFkQubXIjrfbtm1bew4bIAAC2hOAMGrP3ClGbi22bNmS+FGaHf/6+aFYnCBhBwQ0JoA7UGPgrtHxo7PUWuRz3DPNwsiCCQcCIKAPAQijPtxFrEVFRUIEWQhdjQUSDgRAQB8CEEZ9uItYQ0NDRUcLi6CjsUhGR0frmDJEDQLWJgBh1Kn8pUfm+lqG/v7+ohNGp6QhWhCwPAEIo05VgD/JaeizHHzLqFOhIFoQsBOAMOpQFRprLXJyQkJCGhRNHZKLKEHAcgQgjJYrcmQYBECgKQIQxqYI4TwIgIDlCEAYVS7yq1evqhwDggcBEFCaAIRRaaL28IYPH0633367+D7xd7/7HY0dO1almBAsCICA0gQgjEoTJaLk5OQ6H2w3a9aMjh49qkJsCBIEQEBpAhBGpYkSUZ8+feoII3+0PWTIEBViQ5AgAAJKE4AwKk2UiPr371+vMPb/PEKF2BAkCICA0gQgjEoTJaL4nH3k1+JOZ3G86x7ym7KDBm89SKcuXFYhVgQJAiCgFAEIo1Ik7eHsOllJf56fSX/4egH98X//j2655RZq06YNbbIl0LBtxUIc/ytqF03afVzhmBEcCICAUgQgjEqRJKK0E5X0p/mZ9JeFWZRbWlVvyHtKq+jFuEIhkI8vz6U1BzG9WL2gcBAEdCQAYVQIfsrxCvqfXzPob4uyiMWvKbe6qIzuW7xbCORrG/fRnrKmr2kqTJwHARBQhgCEUQGO245VUMC8DCF0+WUX3ApxfOYxunV6KjWbsoPCUw/TpavX3LoenkEABJQnAGH0kunWY+fo7rnp1HbJbipwUxSlqEurL9P7iUWi9dhmQSbNzT8lncIvCICADgQgjF5ATzp6jv4wJ53+sTSbCs+611KsL9rUE5X0bMweIZCdVufT1qPn6vOGYyAAAioTgDB6CDjhSDlx7/JDS7NprwKi6JiMhYWnqfW8DCGQA5KK6Oj5S46nsQ0CIKAyAQijB4BtJeV01y+76OHfsml/ebUHIci75Ou0EiGOv5uVRvwuEg4EQEAbAhBGNzmzKLb6eSc98lsOHVBRFKVkHTxXTa9t2CcE8sGl2bTyQKl0Cr8gAAIqEYAwugGWRfHfZ++kR5flUNE59VqK9SVpc0k5/XNZjhDIXvF7affp8/V5wzEQAAEFCEAYZUJkUfSflSbEiVtxerkZuSfoP37eKQTyix2HqPIy5nvUqywQr+8SgDDKKFsWxTtmpVG75TlUXHFRxhXqeqm6fJWGJNcML/zjnHSanXdS3QgROghYjACEsYkCZ1G8fWYqPbY8lw4bQBQdk5t95jx1W1sgWo9PrcwjftyGAwEQ8J4AhLERhiyKzWek0uMrcqmkUv+WYkNJ5Q4ZHorIs/e8YztAxTo+6jeURhwHATMRgDA2UFosirdMT6EnVuTSEQOLomPyx2YcFWm+cWoKjUk/4ngK2yAAAm4QgDDWA4tF8eZpKfRkdK7pPq4+fv4SvZdwQLQe712YRb/tO1NPDnEIBECgMQIQRhc6LIo3TE2hoOhcOmbiESfJxyqo/ao8IZBd1xQQzxMJBwIgII8AhNGBE4siv6cLjs6jE1W+MQxvXv4pusc+vPCT5GIqq77ikGNsggAI1EcAwminIoki9+6e9BFRlAqcZzKLSD0sRL/l7DSalnNCOoVfEACBeggYUhiLioooIiKC+vXrJ2zChAnEx9Rykig+vTLPp9dj4RmAXrUPL+Rx3vGHzqqF1OtwbTYbJSQkCCsrwyznXgNFAG4RMJwwhoWFiUWkAgICKDQ0VBhvh4eHu5UxuZ4lUeT3cactskjVuuKz9Ih9eCELpdKzA8ll35A/FkJebtbRWrZsKf4sG7oGx0FASQKGEkZJFCMjI5XMY4NhSaL4zKo9dKbaeiv3Tck+LsZ+83vViNQSMsrk4dxaZFGUnhL4l+sEH4uKimqwPHECBJQiYBhhlG4GrSq+JIo8MWyZBUVRqkBnL16hj7fWDC/877nptKDwtHRKt19+OvD3968Tv5pPDnUiwwFLEzCMMIaEhFBQUJAmhSGJYoeYPcTCAEficx7+rIdbj0+vyqPtxyt0w8J1gc3RSY/XWj1NOMaNbesRMIQwalnpJVF8bvUeKoco1qnxS/edob8urBleyB+K69FDz61Fx3fK0dHR1LZtWwoMDCR0xNQpMhxQgYAhhFF6jOZfNZ0kih1X59O5S2gpNsZ69K4jYvTPTdNSaFzm0ca8KnqO3yc6drpI245CqWiECAwE6iFgCGGUXqzXkz7FDkmi2Dk2nyogirK4Hqq4SG/ZaoYXciuS18JW23HrkMVQahlmZGSI1iMf43NwIKAFAUMII3e4cMWXeiGVzrgkis/H5tN5TOzqNl7mxx++8/vHkLUFlFda5XYYci/gLxP4kdnV8ftnrd5Bu8aNfesRMIQwSo/SavRIS6LYJTafeIJXOM8J8IS43HPNAjl0WzFVX7nmeWANXMnix9+vujoIoysR7KtJwBDCyBnkit+6dWviRyelnCSKL6wpoAtXIIpKcGWOvKQCi+Ods3fSzFxlhxfyk4NrzzPXCf7A2/W4EvlBGCBQHwHDCCNXfn6E4huDeyCDg4PFzeDpS3dJFPkTFDVaNvXBtNKxnDNV1DN+rxBIXhyM19n21nEd4PLnoaA8JJRt0KBBoh7gMdpburjeHQKGEUYp0fxYzWLIxi/bpZfw0nk5v5Io8vuwi0YZziEn4Sb0E1NUSg/9li0Esu+GfV7NdM5lLz0yS79cD9T+WsGE2JFklQkYThi9za8kirwWymWIorc4ZV8fmXmMeOYefsQemVYi+zp4BAEjEvApYZRE8cW4QrpyTfmOASMWoJHSxB+Df5hUJMQxYF4GLdqr//BCI/FBWsxDwNTCuGDBAjF0bODAgSSJYve4QsNMhmCeaqBsSnk4YafV+UIgeYIOx9nDp02bRrNnz1Y2QoQGAgoTMK0wvvDCC+JFPb+sFxbwF+q6IoPQTlS4hngR3PyCU9RmQaYQyOcnL6dbmzevLbMWLVpQenq6F6HjUhBQj4AphbGioqL2BqsVRj8/erhTiOgdTTxyjtiSjp6jLXbbevQcJR9jq6BtduOWzQ67pZyooFRhlZR2opLSTlbSzpOVorXDLZ70U5WUceq8sMxT5ynz9HnKOn2edtst+0wVcU8tWy5baZX4EHpPaRXtKaui/LILVGA3njCW50Bk28dWXk37y6vpgN2KzlXTQbvxUqjFFReJR6HwutZsvJQrr1zIdvT8JWG8Pg0vhHW86pJYloEfa09WXRYT7/I8k2xn2KovU2n1ZTGjEC9zwJNo8JhxNh4mycYjgyovXaXKy1fFB/H8/Scbf6rDxr38F9muXqNLV6+Jd7n8PpdfX7Dxq11+k03vYzMAAAW4SURBVCH9SX2dVkJ+gf+qU2Zt2rRRr2YjZBDwgoAphXHp0qV1bjIhkA8+K1on3AEAMxiD5i3qlNlNN93kRdXFpSCgHgFTCiPjaNasWZ0b7fFuPcW7Rn7fCDMWg+Z3tqpTXr///e/Vq9kIGQS8IGBaYeSPgB0fo1u1auUFBlyqNoGPP/7Yqby47MaMGaN2tAgfBDwiYFph5NympKTQgAEDaPz48R5lHhdpS4C/IuAPt9u3b08xMTHaRo7YQMANAqYWRjfyCa8gAAIgIJsAhFE2KngEARCwCgEIo1VKGvkEARCQTQDCKBsVPIIACFiFAITRKiWNfIIACMgmAGGUjQoeQQAErEIAwmiVkkY+QQAEZBOAMMpGBY8gAAJWIQBhtEpJI58gAAKyCUAYZaOCRxAAAasQgDBapaSRTxAAAdkEIIyyUcEjCICAVQhAGK1S0sgnCICAbAIQRtmo4BEEQMAqBCCMVilp5BMEQEA2AQijbFTwCAIgYBUCEEarlDTyCQIgIJsAhFE2KngEARCwCgEIo1VKGvkEARCQTQDCKBsVPIIACFiFAITRKiWNfIIACMgmAGGUjQoeQQAErEIAwmiVkkY+QQAEZBOAMMpGBY8gAAJWIQBhtEpJI58gAAKyCUAYZaOCRxAAAasQgDBapaSRTxAAAdkEIIyyUcEjCICAVQhAGK1S0sgnCICAbAIQRtmo4BEEQMAqBCCMVilp5BMEQEA2AQijbFTwCAIgYBUCEEarlDTyCQIgIJsAhFE2KngEARCwCgEIo1VKGvkEARCQTQDCKBsVPIIACFiFAITRKiWNfIIACMgmAGGUjQoeQQAErEIAwmiVkkY+QQAEZBOAMMpGBY8gAAJWIQBhtEpJI58gAAKyCUAYZaOCRxAAAasQgDBapaSRTxAAAdkEIIyyUcEjCICAVQhAGK1S0sgnCICAbAIQRtmo4BEEQMAqBCCMVilp5BMEQEA2AQijbFTwCAIgYBUCEEarlDTyCQIgIJsAhFE2KngEARCwCgEIo1VKGvkEARCQTQDCKBsVPIIACFiFAITRKiWNfIIACMgmAGGUjQoeQQAErEIAwmiVkkY+QQAEZBOAMMpGBY8gAAJWIQBhtEpJI58gAAKyCUAYZaOCRxAAAasQ0FwYi4qKKDg42MkiIiKorKzMKsyRTxAAAYMT0FwYo6Ojyc/Pj2w2m7CwsDDy9/enbt26GRwVkgcCIGAVApoLY3h4OAUEBDjxjYqKEmLpdBA7IAACIKATAc2FMSgoiEJDQ52yK7Ui+TEbDgRAAAT0JqC5MPJjdGRkpFO+pcdpp4PYAQEQAAGdCGgqjBkZGbXvFzm/3OHCHS8slvyIDQcCIAACRiCgqTBK7xK5V7ply5ZCELnjBaJohKqANIAACEgENBVGfmQODAys7ZHmFiQcCIAACBiNgKbCyKLI4ggHAiAAAkYmoKkw8rtEfpyGAwEQAAEjE9BMGPmDbhZGPD4buTogbSAAAkxAM2HkT3S4owUOBEAABIxOQDNhNDoIpA8EQAAEJAIQRokEfkEABEDATgDCiKoAAiAAAi4EFBHG8vJy6t27N914441011130YgRI1yiwS4IgAAImIeAIsLYo0cP0ePMvc6STZkyxTwUkFIQAAEQcCDgtTBWV1fXiqEkivzboUMHh2iwCQIgAALmIeC1MHJWb7vttjriiIlnzVMJkFIQAAFnAooI46BBg+oI4/Lly51jwh4IgAAImISAIsLIeR09ejS1a9eOOnbsSEuWLDFJ9pFMEAABEKhLQDFhrBs0joAACICAOQlAGM1Zbkg1CICAigQgjCrCRdAgAALmJABhNGe5IdUgAAIqEoAwqggXQYMACJiTAITRnOWGVIMACKhIAMKoIlwEDQIgYE4CEEZzlhtSDQIgoCIBCKOKcBE0CICAOQlAGM1Zbkg1CICAigQgjCrCRdAgAALmJPD/LBggS3F5ACIAAAAASUVORK5CYII=[/img][br][br]What do you think is true about the angles in [math]A'B'C'[/math] compared to the angles in [math]ABC[/math]?
Use the tools available to figure out if what you thought was true is definitely true for these triangles.
Do you think it would be true for angles in any dilation?
[size=150]Dilate point [math]A[/math] using center [math]C[/math] and scale factor [math]\frac{3}{4}[/math].[/size]
[size=150]Dilate point [math]B[/math] using center [math]C[/math] and scale factor [math]\frac{1}{3}[/math].[/size]
[size=150]Dilate point [math]D[/math] using center [math]C[/math] and scale factor [math]\frac{3}{2}[/math].[/size]
[size=150]Dilate point [math]CE[/math] using center [math]C[/math] and scale factor [math]2[/math].[/size]
What happens when the center of dilation is on a line and then you dilate the line?
Here is a figure.
[table][tr][td][list][*] [math]X[/math] is the midpoint of [math]AB[/math].[/*][/list][list][*][math]B'[/math] is the image of [math]B[/math] after being dilated by a scale factor of 0.5 using center [math]C[/math].[/*][*][math]A'[/math] is the image of [math]A[/math] after being dilated by a scale factor of 0.5 using center [math]C[/math].[/*][/list][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAPEAAACwCAYAAADez4jAAAAZp0lEQVR4Ae2dCfxVw/vHhVLaZE+LVlS2VpVC9l2W7JJESMgeRdnaUJElJFvKWpaiRSQVoVWRFpUWW6lQSM3/9Z5/8/2dzvcu597vOfeeOed5Xq/7uveeM2fmeT7PfM7MmTPzzA5KRBAQBKxGYAertRflBQFBQAmJpRIIApYjICS23IGiviAgJJY6IAhYjoCQ2HIHivqCgJBY6oAgYDkCQmLLHSjqCwJCYqkDgoDlCAiJLXegqC8ICImlDggCPiEwadIkVbZsWdWwYUO1evVqn3JNn42QOD1GkkIQSIsABC5TpoyqX7++WrVqVdr0fiYQEvuJpuQVSwQ+/fRT3QIffvjhauXKlTnHQEicc8ilwCghMHnyZFWuXDkFgVesWJEX04TEeYFdCo0CAp999pkqX768Ouyww9SPP/6YN5OExHmDXgq2GYEpU6ao3XbbTR166KFq+fLleTVFSJxX+KVwGxGYOnWqJvAhhxyili1blncThMR5d4EoYBMCELhChQrq4IMPDgWBwU5IbFMNEl3zisC0adPU7rvvrurVq6eWLl2aV12chQuJnWjIb0EgCQKff/652mOPPTSBf/jhhySp8nNYSJwf3KVUixD44osv1J577qnq1q2rlixZEjrNhcShc4koFCYEpk+frvbaay9Vp04dtXjx4jCpVqCLkLgACvkhCGyPwJdffqkJfNBBB6lFixZtfzJE/4TEIXKGqBIeBCDw3nvvrQ488MBQExjEhMThqTeiSUgQ+Oqrr9Q+++yjDjjgALVw4cKQaJVcDSFxcmzkTAwR+Prrr9W+++6rCfz9999bgYCQ2Ao3iZK5QGDGjBmqYsWKqnbt2mrBggW5KNKXMoTEvsAomdiOwMyZM9V+++2natWqpb777jurzBESW+UuUTYIBGbNmqUqVaqkatasqb799tsgigg0TyFxoPBK5mFHYPbs2ZrANWrUsJLA4CskDnstE/0CQwACV65cWVWvXl3Nnz8/sHKCzlhIHDTCkn8oEZgzZ46qUqWKJvC8efNCqaNXpYTEXpGSdJFBYO7cuapq1aqqWrVq6ptvvrHeLiGx9S4UAzJBANLuv//++gOZoyBC4ih40UIbeKXzySefFHz4H7TQbab1pRWmOx0VERJHxZOW2XH00UerHXbYYbsPBAuKzAxckT/PwVEiMG4XEltW+aOiLgTu379/gTkstKebe9ZZZxUc8+sHBGYEmpFoRqSjJkLiqHnUAntobSGxu9W99957NZH9NIHJG7wDhsBM6oiiCImj6NWQ20QLDIndQvxmP1tipk8yC4vZWO4bhrtsm/8XRtJma0R3KxC4/PLL9Y4JzoGt1q1b61bYr/hVLGBgHjTzoVnYEGUREkfZuyG1jRbXPagFif0SlhCyEokVSSwtjLoIiaPu4RDaB4FHjhxZoBmtL8T2g8gs4ofArAmOA4EBUUhcUJXkRy4Q+Pjjj3Ur7O42Dx06VB///fffs1YDAhONg6gcROeIiwiJ4+LpkNjJCDSbkLkl2WCXO12y/wSyIx4WBCY+VpxESBwnb4fAVkafmejhFFpftgZ1H3emSfWbULJEpCSwHSFm4yZC4rh5PM/2MqHjmGOOUT169NAffrO7IMfdXWwvqhLMnZjQxIYmyHscRUgcR6/n0Wa60+4Pz8PZCKRnVwZ2Z2CblbiKkDiunrfcbjY0g8DsjxRnAuNGIbHllTmO6kNgdiZkh0J2Koy7CInjXgMssH/r1q1q1KhR6o033tCRKNkbGAKzV7CItMRSB0KOAAsYmP9sZnjtvPPOqmzZsmrKlCkh1zx36klLnDuspaQsELjkkksKCGyI3Lhx4yxyiu4lQuLo+jYSlrGM0JDXfO+6666RsM0vI4TEfiEp+QSCwGmnnVaIxC1btgykLFszFRLb6rkY6L1y5Uo9F7pYsWIFRN5pp53UBx98EAPrvZsoJPaOlaTMIQKrVq1S9evX14NY7777rp4gQnd68ODBOdTCjqKExHb4KVZarl69WjVo0ECVKVNGR8PEeF4z0Qr37NkzVlh4MVZI7AUlSZMzBH766SfVsGFDVbp0acWyRaew5rhNmzbOQ/JbZmxJHQgTAj///LNq1KiRYvR54sSJhVS79NJL9WqlQidifkBa4phXgLCY/8svv2gClypVKiGB0bNPnz56gGvjxo1hUTsUegiJQ+GGeCsBgZnAUbJkSfXRRx8lBWPMmDGaxHFcM5wUFOlOp4JGzuUCgV9//VU1adJE7bLLLmrChAkpi1y+fLkm8ZAhQ1Kmi9tJaYnj5vEQ2fvbb7+pI444QhN4/PjxnjRj6WGXLl08pY1LIiFxXDwdMjvXrFmjmjZtqkqUKKHGjRvnWTsigRx//PGe08choZA4Dl4OmY1r165VzZo1U8WLF1djx47NSLvOnTvrYHgZXRTxxELiiDs4bOYRFA8Cs6QwUwJjCzO2mLnFjC6R/0dASCw1IWcIQODmzZvrmVcffvhhVuUSCAASZ3MDyKpACy4SElvgpCiouG7dOnXkkUeqHXfcsUgLGP744w9N4kceeSQKsPhig5DYFxglk1QIrF+/XrVo0UITmHe9RRU2SmvXrl1Rs4nM9ULiyLgynIZs2LBBsf6X5YSjR4/2Rcmzzz5bz6/2JbMIZCIkjoATw2oCXd+jjjpKd3/ff/9939Ts3r27frfsW4aWZyQkttyBYVX/zz//DITA2Pv666/rG8O8efPCan5O9RIS5xTueBQGgdlXiVHk9957z3ejiYBJ3q+99prveduYoZDYRq+FWOe//vpL77UEyYjIEZSwWKJbt25BZW9VvkJiq9wVbmVZItiqVSvdSr7zzjuBKsu6Y3ZYFJHg8VIHfEJg06ZN6thjj9UEZreGoOWKK67QQeWDLseG/KUltsFLIdfx77//Vscdd5wm8MiRI3Oi7aOPPqrL4x103EVIHPcaUET7//nnn5wTGJVZushzt2znIt3pIlbh8F4+c+ZMxVzlIAUCsywQMr399ttBFlUobyJiUu7TTz9d6FzcDkhLbKHH2Vz7k08+2e7jJuz++++v+vfvH5h1//77rzrhhBM0kd56663AykmV8b777qs6deqUKknBOfABMzdOJOCGx8dWERJb6LnLL79clS9fXr+Lhay0SLvttpsyz6NUSM4nqrB+mLt582Z14okn6nLffPNNP7LMKg9uIryP9iqJbmyExQU/d3hcr3mGIZ2QOAxeyFAH4i/feOONBVdBViozREbuvfdeBdGDkP/++0+ddNJJuuKzX3A+5eabb9b7FHvVAVyqVatWkBzcwCzIHktBYQH+EBIHCG4QWVPxaDlMq2vKoCJyHIHkdLn9li1btqiTTz5Zl8PUx3zL0KFDtS7Lli3zpAqYgJHpOoNTUDc7Twr5lEhI7BOQucrGdP/cJGXiA91FSB7EJAi2UQkTgcH7yy+/1KTMZHEFPRZ6MZAXEoOX7SIktsyDdAlpTZwDW6yt5RmYFgZy+/18B4FPOeUUXW6Y5ivzfhosevXq5dmLtN50ocHLfSP0nEnIEgqJQ+aQdOrQylJxnZ/DDz880Bbl1FNP1eWNGDEinXo5P1+nTh11ySWXeC6XxxCw42YYFRESW+ZJuszOCmi6zxA5CDGbfA8fPjyI7Iuc5/nnn68OPfRQT/nQ8tIK06V2DnB5ujjEiYTEIXaOWzUqIa2Iu7tsnpPdx93XZ/r/9NNP1+W9+uqrmV6as/T33XefjhrCoFs6MQNZBkczwJXuurCfFxKH3UMO/UxX0D0YY0jsZ6U844wzNIGHDRvm0CB8Pw0ms2bNSqkcg1nOgSx+O1/Tpbw45CeFxCF3kFM9utF0p50CodkVwX3cmSbT37YQGLsWLVqkbzavvPJKUjMhuhn4M4l4JWfeq5tjtn4LiS3ynHmW69Gjh+IDeamIENivVvjMM89MS4qwQVa2bFl1xx13JFQLXMCIUWmnmC41BLddhMQWeZDWg9bY+fGzEpqR75dfftkiVJQOSM8IeiIBn2Qzsjju9zhCIh2CPiYkDhphS/Jv3bq1boFfeuklSzT+n5pXX321qlKlyv8OxOyXkDhmDk9kLnGcGfV+8cUXE50O/bHHH39c689WqXEUIXEMvU4EyieffFLNnj1bnXPOOZoAL7zwgrVIfPDBB9qGrl27KjYtj5sIiWPmcRNGxznjy2YCf/3112rvvffWJMamcuXK6SmpcXKrkDhG3h40aFBBZTckZoMzdmqwVc4777xCNsVtE3Ihsa21Nwu927dvX6jCQ+Zp06ZlkVs4LiG6h7khmW9eOcVJhMQx8vYTTzxRqMKz2beNLTGruNq0aVPIHogcy5Y41WyXGNXxyJvKYgHTWplv2/b5JSCfea6vVKmSuv7665WzNaYVnjRpUuR96TRQWmInGhH+fcEFF2gCP/vss4pF9ExDvPjii62x+LnnnlP169fXNhxyyCHbRblk76eHHnpIn7PxPXdRnSAkLiqCFlzvJLBRN9Mgc+a6dN9EzPBrFhT7OvXt21dPK6XnwLTTZGGBWMXEIB2rmuImQuKIe/zCCy/ULdQzzzyznaUEmdtjjz22O5bqDyt+Ek1f5LhZDWTmI/NdFPnxxx/VnXfeqegaQ14mo0yYMCFtlqwr5pEhbiIkjrDHL7roIk2CwYMHF7Ly+eef1+e8BpmDwO5VPywqcK4OIk1R4nsx+YQplOZ5/corr1QzZswopHuyA0T4INJH3ERIHFGP87wLGZLtkJBpkDmWPJKfWXDB6iDnf2CEwNl0pbnGvO/ddddd1W233aaWLl2asWd69+6tdSL2VpxESBxBb9MiQbCnnnoqqXUmyBwV36tAUp55ITThbdxhgjJd08zOEWYnxcqVK+uAdxs2bPCqTqF0DNhhNzeoOImQOGLevvTSS3VFZm50OskmyBxdatYxu7vNtNDuNbvJymeEnJhgEI7n2ETd/WTXpjrOowF58qgQJxESR8jbmRAYsxkEIkxNJsIzMC2uO0SQ+787TyaU9OnTR1WtWlUTjRtBEDtI7L777opBuziJkDgi3r7ssss0OZiV5VV4HcNrGS9B5siTgStaOvcAV6ryaB2JulGmTBl9LaumPvroo1SXFOkcr6F4fRYnERJHwNtt27bVBGGBQyZCFxhSpgsyR57OgSyuMQNcycoj/VVXXaXzJ32HDh18CyGUrEyOmxlcqdJE7ZyQ2HKPMtAESVgYn6l4CTJHnu6BLDPAlag8Wtlzzz1X61S6dGl1++23K6+vsRLll+kxRuPBg/2L4yJCYos9zfYtVNjHHnssaytSBZkzmUJauqlGGMCiXOdzMM+3rVq10scJlcOodz4WVkyZMkXrMG7cOKNu5L+FxJa6+IorrtCVdeDAgUWyoHnz5opdHpIJr5EYzHISlt+QGDIzE4zBMf7z7Z4ZlizfoI7zigpdHn300aCKCF2+QuLQuSS9QmZdcFEJTEnMkGLEOJEwCQNCuCdwQJS6deuqUqVK6fO0wPncbNyte82aNRU3ubiIkNgyTxsCDxgwwBfNMwkyxywqnnF51oXcPPtOnDjRFz38zITInY0aNfIzy1DnJSQOtXu2V465xJAn0UKE7VN6/2daWxbZJxPmLzO6TNl8GHX2MqKdLL+gj3fr1k2VLFky6GJCk7+QODSuSK2IIZHfz3qEeYWYiUa3WTlkomGaAbDly5enVjQEZ9lDGZvmz58fAm2CV0FIHDzGRS7BvG8NIgoHsaZLlCihdtllF8W6Y0jKml1mVEEEnpeZacXCe1sE8qJ7srXHttjhVU8hsVek8pTOLM17+OGHfdeALjSV3fkxz7vMbWaOs63CTal79+62qp+R3kLijODKbeKOHTtqggVBYCzp0qXLdgQ2ZC7Ke+fcIpS8NAa2GOCKgwiJQ+plQ+B+/foFoiHRNxo3bpyQxAsWLAikzFxmykSYWrVq5bLIvJUlJM4b9MkLvuaaazS5iC/lt7BjgnlNZVpe53dUwr0yfoBd+Zg15rfP0uUnJE6HUI7PX3vttbryMZjkp4wfP153L6nYbHVCDCtiWbEw/6ijjtJlNmzYUK1Zs8bPYvOW19ixY7VNU6dOzZsOuSpYSJwrpD2Uc9111+mKl0m0jXTZ8rrFkJRoHLTuRJF0SxBB5ljJVNSgeW49vf5ftWqVxtKvgANey81HOiFxEtSZBNGjRw/9qoUBEmZIBVkhO3XqpCtdr169kmiU2WFC8xx88ME6zwYNGijiNqeSogSZAxdGup3zqymLudTOED6pyg/iHEHlWZqYjXADSjUBJps8g7pGSOxClopo3pGycodKSEhWoll4DT/jyjLtXyoa3dyiEnjdunXqwQcfVOyMQH4837JjghehbK7JJsgcOHGtc441xOZYkDe+dHZhP77MVKgDBD5AfxvEDi1ziCSthzMMa9BFGwKzg0G2smTJEnXLLbcULEhgj6JMW5Fsg8wRHMCE7HEGCuCG547Dla192V7HK7RMYmubclijjU2Q2N27MGnC9C0kdnjDhJ+hK5UL6dy5s64otJ7ZyFdffaVX61DZ+PBaas6cOdlkpUPEkkemQeboodBbMb0WUzgEdrbM5nguv4cMGaJxyWSqqOlBmDnl+bbBC15CYgdK3H25C+dCbrjhBl3BHnjggYyLY8E7JIF06Ny1a1e1YsWKjPNxX0CrlUmQOVpbyqe1gsRmJwjy5X++Zfr06Rqj0aNHe1YF/xvdwdfZu/CcSY4TCom3AY6zcFouWmEqO2Xdf//9Gbl7xIgRqmXLlvra6tWrKyaCbNy4MaM8UiWm8noNMmeeG83AFTaZyk9rFobKv2nTJo2V19d17tbX9DJSYRaGc0LibV6gMkKsoOWmm27S5WSy8RcxpOvVq6ev410u3cQghBHyihUresoavEwrzAX8Z7512OSggw5ShPL1ItyEnM/x/Hf2LrzkkY80wdfafFiVRZmmUmZxqedLzFxlLwSmpaOrDam4udBCBt26eQ0yZ1phRn55DWdexeXiJugZ7G0JGeRjsDKdmFaY6ZrGJt6rm95FuuvzeV5IvA39oFtiQ+CePXum9PfixYv1cymrcCAFywNztWn2Z599pstMF2SO1olWmApuPhAFfSF4mAS8ia29devWlGrRdeZj7OGb/2HsXbgNERJvQ4RBGiphEM/EDBaRN3f4ZML+QSZ6JWmZfjl37txkyQM5vn79eq1nqsADZvTW/c7cHA/baC7vycGTHReTifE9NjjFvK1wHgvjbyHxNq/QgtC6cOd1tyZu52biSN7fUolo6RMJc3zPPPNMnYYJBnfffbdauXJloqQ5OZYuyByjt7RQiQQ7g+7yJyo31bGFCxdqbIcNG5YwGb6m25zo2dd0sd31IWFGeTwoJHaAj9MgMpWR5z0zcysZAR2XJvx566236rzuueeeQueHDx+uWrRooc/XqFFDseqG0dR8C1NMWaKYSEylTtbagl22WCUqz69jbCHDgo9Egr7onYio9MqoC8nsTZRfPo4JiV2o40y6VziXT7YOZI9dKoA7ugR7JRHulXMsXHd3S13q5PxvqiBztLKpgvRhS7Z4BWlos2bNksbWxp5UvQfqQFF6YkHaZfIWEhskfPwmrCskhRDI2rVr9TthJuRz/MQTT1TvvPOOjyX6lxXvotExSkHmiFGWLLa2f8jlLychsc/YOwnMXkeMShOIDmJceOGFavLkyT6X6G928+bN07pGKcgc4YbAPyprpd0eFxK7EcnwP69jWLxAy8oWnlQWdh9gAIjffFgnDDlskeLFi+sVUNOmTbNF5ZR6sjsFfuCGmsk86pSZhuikkLgIzjBhdAxZ+a5du7auMBUqVNDdaZt259u8ebNq2rRpwc0He7JdnFEEWH29lJ6PieCJPfSKiHISJcmKxGPGjFFx/5jtT5wE5jc71fMMRstsG0YmvrXTpmLFiukQPrbZYvRt0qTJdjclbOM1ojlvy3eqm05WJHY6WX5vH7dZ8BA8gqgDvpOYfXji/jEzgdwOI6aTrdjcddddhVotdj5kNpmtNjHn3O0jYo7ZZo/vJE6VYVzOMbPKXTnYrcF2Ya9ip13E6rJZmLrKsk1jE6GLuClFSbLqTkcJgGxs4f0vlYLXSUTSIBoGC9CjIkzYePnll0M/ycEr3lu2bFGjRo3S8cb++ecfr5dZk05InKGrmIEFgZmRJSIIhAEBIXEGXmAONARmTrSIIBAWBITEHj3BHFoIzKokEUEgTAgIiT14g3XAEDiTIHIespUkgoAvCAiJ08AoBE4DkJzOOwJC4hQuILQLLTBzbkUEgbAiICRO4hmC2UFgolOKCAJhRkBInMA7xIOGwIlCtiRILocEgbwiICR2wU+YWAjMDg0igoANCAiJHV5i2R0EZo8kEUHAFgSExNs8JQS2pcqKnm4EhMRK6cgctMDZbkjtBlX+CwK5RCD2JDaba7MPkYggYCMCsSZx79699TMwMbBEBAFbEYgtidnuki4026WICAI2IxBLEvft21cTmEB3IoKA7QjEjsRCYNurrOjvRiBWJO7Xr59ugTt27OjGQf4LAtYiEBsSP/zww5rAUYiDZW1tE8UDQSAWJGbHQQaxiKssIghEDYHIk5gNsyFwhw4douY7sUcQ0AhEmsRmp/crr7xS3C0IRBaByJJYCBzZOiuGuRCIJIkHDBigu9Dt27d3mSt/BYHoIRA5Eg8cOFATmO1FRQSBOCAQKRKbzaTbtWsXB9+JjYKARiAyJDZbjbK5t4ggECcEIkHiQYMG6S5027Zt4+Q7sVUQ0AhEgsTiS0EgzggIiePsfbE9Egj8Hy9ELQUpseGuAAAAAElFTkSuQmCC[/img][/td][/tr][/table][br][br]Call the intersection of [math]CX[/math] and [math]A'B'[/math] point [math]X'[/math]. Is point [math]X'[/math] a dilation of point [math]X[/math]? Explain or show your reasoning.[br]
Jada dilated triangle ABC using center P and scale factor 2.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUMAAAEXCAYAAAA3LCbmAAAgAElEQVR4Ae2dCXhVVZqu4WqXQ7UNt9Sq29V1gbq3vWXbllCWaKGloUuZVAiDA4gYUAoQ1OBsgRhKC+0SkXJkEAyIDIIYhoQhkIEhkISQAAmEJJCEBBICCYEkQEgg/32+dbLjIRPnZA9nn32+9Tz/c4a9xnft85211177X+2EgQRIgARIQNqRAQmQAAmQgFAMeRKQAAmQAAhwZMjzgARIgAQohjwHSIAESMBFgCNDngkkQAIkwJEhzwESIAEScBHgyJBnAgmQAAlwZMhzgARIgARcBDgy5JnglwS6du0qcXFxfll3VtqeBCiG9uwX1qqeQFBQkLRrd/lpmpaWpr7Ly8sjJxIwjMDlZ5lh2TIjEtBPICIiQjp37qyEr7y8vCHDsLAwCQkJafjMNyRgBAGKoREUmYcpBCCEED6MDN0viXGJjNEhAwkYSYBiaCRN5mUYgfDwcOnQoYNgRAgxxCgRAZ9x6cxAAkYToBgaTZT56SYAwevYsaMaFSIzbYSI9xBJGAMJGE2AYmg0UeanmwAujSGAWsBIMDQ0VPvIVxIwhQDF0BSszLStBLRR4cSJEyU+Pl5Zz549eWncVqBM5zEBiqHHqBjRCgK4S4w5wsbWrVs3K4pnGQFMgGIYwJ1vt6Zj3SBEsPGc4MyZM9X3dqsv6+MsAhRDZ/WnX7cmODi42cthLKuBSOISmoEEzCJAMTSLLPP1ioAmeO7rCbUMtCdOmjumxeErCeglQDHUS5DpDSFwpadKcEeZC60NQc1MWiBAMWwBDL8mARIILAIUw8Dqb7aWBEigBQIUwxbA8GtzCGRmZkpKSoo5mTNXEtBBgGKoAx6TekegU6dODesHb7rpJklPT/cuA8YmARMJUAxNhMusfyTQvXv3BiHUFlRDHBlIwC4EKIZ26QmH1+Oaa65pIobt27d3eKvZPH8iQDH0p97y47reeOONTcTw2p/9RErPl/hxq1h1JxGgGDqpN23altq6Wun1Vo8mYvgfY34lg9b1kOU5dMll064LqGpRDAOqu61vbM2lGpmS+IL0Wn27vDx9vNx2221yyy23yOTJk+V87Tn5Yt/78uCq22Rc/GOy9Vi09RVkiSRQT4BiyFPBNAIXLlXL5MTx0nv1b2VrUctCd+j0QZm083klilOTJ0p2+X7T6sSMSaAlAhTDlsjwe10Eqi+el0k7x0nv1XfItqJNHuWFkeHIzY8oUZydMV0qLpz2KB0jkYARBCiGRlBkHpcROH/xnLy1Y4z0WdNVthdtvuyYJx+WZc9TIvrkhp6yKneJJ0kYhwR0E6AY6kbIDNwJnKutkjd3jJa+a7pJQnGM+yGv3p++cEo+TntHjRJDtw6XxONbvErPyCTgLQGKobfEGL9FAlW1lfJ6wnPSb83vZEdxbIvxvDmwv2yPvLp9lBLFD1LelPyKQ94kZ1wS8JgAxdBjVIzYGoHKmgolWg+vvVN2Fse1FrVNxzYVrJFhGx9Uohh+4FPBnCQDCRhJgGJoJM0Azaui5rS8sj1ElBAejzeVwsLMz5UgjtjUR9YdWWlqWcw8sAhQDAOrvw1v7ZkL5TJx2wh5ZO3vLZvXKzlXJO+nvKFE8fWEZyX1ZKLh7WKGgUeAYhh4fW5Yi3GTAzc3Ho28S5KObzUsX08zggi+sGWYEsUZae9I0dlCT5MyHgk0IUAxbIKEX3hC4FR1qby49SnpH9ldkku2eZLEtDiRectlyPo/qjvYi7PmSJ3UmVYWM3YuAYqhc/vWtJaVVZ+UCVuGyoDIu2VXyXbTyvEm44t1tTI34yM1SnwuZoDEFEZ6k5xxSUAohjwJvCJQev6EjI9/QoKj7pGUkgSv0loRuaAyV8KSXlKiiEcB95elWVEsy3AAAYqhAzrRqiacPH9cOVQIjvqDpJzYYVWxbSpn5/F4+XPsICWKn+2bJmXnT7QpHyYKHAIUw8Dpa10tPXGuWMbGDZaB63rI7hM7deVlZeKVh7+RRyO7y4Coe2TFoQVWFs2y/IwAxdDPOswX1cVSFoyyBq27V1L9SAg1VmdrK+WzvX9To8Tn4x/32HGElp6vgUGAYhgY/dzmVhafPSqjY4Nl8Lr7JM3P1/Nlnz6gHEjAf+Jfk1+WnNMH2syFCZ1HgGLovD41rEVYt/dsTH+1bGXPySTD8vV1RvHHNkjI5ofVSHFOxkdSWXPG11Vi+TYgQDG0QSfYsQrHqgqUb8Eh6++XPSeT7VhF3XVakj1XuQp7bP39sjp3qe78mIF/E6AY+nf/mVL7o1X5ErK5n0Ak9pbuMqUMu2R6qvqkfJT2thol4mkaXzxJYxcWgV4PimGgnwGN2l9YmScjNvWVxzc8IPtKUxodde7H9LJU5WwC84kf7H5LjlQcdm5j2bJmCVAMm8USmF8eqcyVp6N7yxMbgiS9dHdAQthYsOpHV2GZn8mFi9UBySEQG00xDMReb6bNcJr6VPRDAlf7GWWpzcQIrK/CMz9Vl85gsv7ID4HV+ABtLcUwQDvevdl5FTkydOOf5MmN/8XH19zAFJ8tlGkprylRfC3hWUlz0B11t2bybT0BimGAnwq5Z7LUaBBiCBf7DE0J4NFDOKbAfOLHaWGCtZcMziNAMXRen3rcosNnDsrjG4LUHNmBU3s9TheoEdfkLVNrLnutvl2WZM0NVAyObTfF0LFd23rDDp3OVEtnMCeWeWpf65F5tIFAzaULMjvjQzVKHLn5YYktjGo4xjf+TYBi6N/916baZ5/erx6vGx7dSw6Wp7cpj0BPlF+RI+8kvahEcdLOcbL/FKcY/P2coBj6ew96Wf+s8gzleWZ4dG/BewZ9BBKKYxtchX2+732B41sG/yRAMfTPfmtTrTEKhFPWpzf1oRC2iWDLieAeDK7CsDHW94cWthyRR2xLgGJo264xtmKZp/ZK/8i7BVts4jKZwXgCcPjwyd531aUzXJ5tL9psfCHM0TQCFEPT0Non4wOn9qgd7J7Z1Jduqyzolqzy9AZXYVOTQwU3qxjsT4BiaP8+0lXDjLI0tbk7HC/wR6kLpdeJY4+ua3AVNnf/DKmqqfA6DyawjgDF0DrWlpeUXrZb+q3ppn6QWFPI4BsC32bNVq7CsGUC1ioy2JMAxdCe/aK7VvA402fNHconIZ4yYfAtgdLzJTI9dbKaT5yw5Umf7zXtWxr2LJ1iaM9+0VUr+CDstfq3MirmUck9k60rLyY2lgD65pXtIUoU3095Q7C1KYM9CFAM7dEPhtUC7vkfWvWfyl0/HDAw2JMAPOEM2/igEsUFmZ8Lnmxh8C0BiqFv+RtaOjZsgjOB52IGCFxyMdifwPwD/1B99sSGnrLhSIT9K+zgGlIMHdK52MtYCWFsML00+1mfHqs6In/b5XIV9vK2Zxy754zdu4ViaPce8qB+KScSlBCOjh3IOSgPeNk1SnLJtgZXYdNT35bjZ4/ZtaqOrBfF0M+7dVfJdiWEeOKhoDLPz1vD6oPAqtwlylUYRvrYwY/BGgIUQ2s4m1IKRhL4wYyJGyyFlfmmlMFMfUOg+uJ5mZX+d9W/T2/qLVjAzWAuAYqhuXxNyz3p+Bb1QxkbN1iOVh0xrRxm7FsCWCOquQp7c8dooRNe8/qDYmgeW9Ny3nk8XgnhuLghgsl3BucT2Fa0qcFV2Cd735NT1aXOb7TFLaQYWgxcb3E7iuNcQhj/mBRVFejNjun9jMDynK+Vq7A+a7rSVZjBfUcxNBiomdklFMcoIXw+/nHBzm0MgUngzIXyBldhz8b0l4SimMAEYXCrKYYGAzUrO/jGw82S8fFPcHc2syD7Wb7wUfnWjjHqvHg7cYIcOk1nHHq6kGKoh55FaTFfBCHEA/5ce2YRdD8qZnPh2gZXYbgDXVVb6Ue1t09VKYb26Ytma7L12EYlhC9sGSol54qajcMvSQAEFh2cpVyF9Y/sLmtylxKKlwQohl4CszJ6/LEN9UI4TE6cK7ayaJblpwRwnmiuwrDaAIvyGTwjQDH0jJPlseKOrldC+OLWp+TkueOWl88C/ZsAvBdprsLe3fWKFPLppCt2KMXwioisjxB7NEoJ4UtbhwucgjKQQFsJrMv/vsFVGDzk1F6qaWtWjk9HMbRZF8cURiohDN36tJSeP2Gz2rE6/kjgUt0l0VyFDVn/R4EvRYamBCiGTZn47BvcFcRd44nbRkjZeW5G7rOOcGjBuFTWXIVh+gVetxl+JEAx/JGFT99FF6xuEEI+auXTrnB84XiufcKWoep8++/db3GVQn2PUwxtcOpvLFilTkw49iyvLrNBjViFQCCwKndxg6uwRQe/DIQmt9pGimGreMw/CFfvuDTGnb/TF06ZXyBLIAE3Audqzza4Chu68U+COetADRTDZnq+vLxc4uLimjli7Ffrj6xUQvjq9pEUQmPRMjcvCRw6ndngKgznY+apfV7m4P/RA1YMIXirVq2SqVOnKktLS2vozZCQEAkODm74bMYbLHnAiPC17aMED94zkIAdCGwtim5wFfZxWphfT9vk5eVJz549PcYakGIYFhYmHTt2lA4dOkhQUJCydu3aSXh4uALXuXNniYgwb6eyqPwVLiFMeFYqak573FmMSAJWEdBchWHb2WU5860q1qtyMGCB2Gk2cuTIy67oZs6cKfgtexoCTgwx6oMIasKngcK/CAJGiN4A1NJ7+ro27zslhK8nPCeVNWc8TcZ4JGA5AdzM+2Tvu+p8fWZTP4HDELsE/F4xgMHvGYMbGAY2+E4byEAsIYiehoASQ0ACrNbmAwHPG4Cegka8NXnL1In1RsJoqaqp8CYp45KAzwjsL0trcBX2l51j5fCZLJ/VRStY+y1juss9dO3aVQkkvsOgp/Fx97iN3weUGGLEh3+S1gL+XbwB2Fpe7sdW5y5VQvjmjj/LWbpYckfD935CwN1V2Gf7psnZ2iqf1Rwjweau4DQxhFiGhoZ6Vb+AEUOMBq80KgQ5M0aFWM+FmyVwxOnLE8irM4ORSaAFApqrsH5rfyc/HF7UQixzv8agpfHABlNf2m8cx7SpL09rEjBiiH8SgLI6RBz+tl4IxwrWdDGQgBMIwMnwh6mT1bk9OjZY8FSLlQGXwF26dGm4edKtWze1AkSbAmvL1Z316mAlMbeyMGRubljtFsXwtysPL1InC+ZZzl88Z3j+zJAEfE0g7WRig6uwsKSXLNm/Gzc5MbBpfPME4ui+RM5bNgEjhgAHWFaF7w8tVEI4aec4wYbgDCTgZALursLmZHwktXW1pjVXuxxuXAAunfWsDw4YMdQuk9syfG4M/UqfVxxaoIRw8s7n5cLF6itF53EScASB2ku1Da7CgqP+IJF5y01pF67yIHyNA37juHxuawgYMdTWJQ0cOLCtrDxKtzwnXAnh24nj5cKlCx6lYSQScBKBI5W5Da7CsJtj6slEQ5uHO8bN3SnG982JpKeFB4wYAog2vMblMlarQxgx8Yp/FCPCdznz64VwgtTQo7ARSJmHHxNwdxUGP4pGbWiG+ULtoQkMcuLj49VvGaNCzhl6ccIAHsQPc4j4d8FSGm9vwTdX3NLseUoIpyS+ILhcYCABEnARcHcVFp75qS4s2hI5CKJmEMG2LKVpXJGAGhk2brxRn5dkf6WE8J2kF+Vi3UWjsmU+JOAYAlU1lQ2uwh7f8IBEF6yyXdsohjq7ZHHWHCWEWFZwiUKokyaTO51AjpursInbnpaMsh+9Rfm67RRDL3sgISFBXnnlFVm2bJl8mzVbCeHU5FCpq7vkZU6MTgKBS8DdVRgWb9vBwzvF0IvzsX///g3zFJiv+OVDHeWvyROlTuq8yIVRSYAENAKaqzA8roqrLNwNvvrqq6V9+/bq5qYWz4pXiqGHlLVV79qkrfY65q1Rsrc0We00tq90l+wrTVGWXrpb0st2S0ZZqjJ4/thftkcOnILtVQZvwrCD5enKssozBJZdvt9lpw9IjrJMgSfiQ6cPyuEzsCzJVZYtuWeyJa8iR1l+xSGBHak4rKygMldclqc2ES+szJejVbAjckxZgRRVFUjR2UIpVnZUis8eFTxqBcPdP9iJc8XKsJn9yfOwErWfM7YyLYNVn5RTykqlvBpWpgzbGMDgvBZWceG08t8I12Uuq1Dee6pqK5XzCjy3fU7ZWTlfe1Y9tYMF6y6rVms2sVypRlmN2gMYN6su1sEuKsO2mLC6OvxF8U/Kw9Pbp9GwARpchf17yC8uG2zgN4blMlYFiqGHpKdMmdKko9BZXYbcpC6V8c9GszcDOCqF9Vp9e739Vnqvht0hfdbAukpfZd2k35puAkcEsIfX3qnskbW/F9ijkXcp6x/ZXVx2twyIgt0jwcr+IAOjYD1k4LoeMmjdvcoGr7tPYNi7GPbY+vvr7QHBTYXHNwTJE8p6ypMbYP8lQzfC/qRs2MYH1YbwT0U/JLDh0b2UPR3dW5Rt6iMjlPWVZzbB+knIZtjDykZufkRgo2IeVfZsTH+BPRczwGWxwYLnjEfHDpQ/KxskY+Jgg2WssiEyNm6IjIt7TMbFPybPxz+uDGsJlW15UiYoGyovbIENkxe3wp6Sl5QNl5e2DhfsCR667Wm1JS62xcVGaLAbOl3X5DeGEaJVgWLoIeno6OgmHQUxHDr+MUk9kSipJ3bKbmU7JOUELEFSShJkV8l2Zckl2wSWdHxrvW2RxOOweNkJK46THcpiZUdxrCQUx0hCUYxsL9qsDI41YZhr2XoMtlG2KNsg8cc2SPzR9RKnbJ3EHV0nsUejlMUURqlNfjYXRgpcMME2FaxRhu1JYdidD4bNqVz2g9poHHu0rMuHfS9RylYIvHRH5i9XTxfAUS0MfhqV5S4VuCpbnbtEVilbLBG5iwXOKn5Qtkh5OVl5+BtZeegbwSOLMDyx47JwwaJ1XDp9p2y+8rK8LHuewJZmf6VsSfZcgeGyCoa5W5fNEnhUwU5v3yj7QhYe/EIWZn6ubEHm57Ig8zMJV/apfH0A9okybLIOm7d/prKv9n8sLpshc/fPkLkZHwkeM5uTMV1mK/tQZqXD/q7sy/T/FtgX6R/IF/s+kM/3vV9v0wTurj7b+zf5VNl78sle2LvK/rHnrwKbuWeqso/3hAnc7c9Ie6fepshHabC3ZXoqbLJykPBh6iSB/X33X5Rhy0/YB8relA9S3pT3U95QNi3ldYFhrZ/LXpX3dsFekXdhyS/LX5VNlKnJsFCZmhQquCkIwyoJ2JSkFwRLx6YkTpC3lY2XyYnjBU9aTVI2TvD4KZ7Fh8FLEwxu61w2WuDL842E5wTOjV9PeFZeUzZKXt0+Sjr8+vomv7GrrrrKw1+o/mgUQy8Y3nnnnZd11o033uhFakYlARJojcDQoUMv+31hsHHfffe1lsTQYxRDL3FOnz5devXqpe4oe5mU0UmABK5AAIJ4ww03yPXXXy99+/a9QmxjD1MMjeXJ3EiABPyUAMXQTzuO1SYBEjCWAMXQWJ7MjQRIwE8JUAz9tONYbRIgAWMJUAyN5cncSIAE/JQAxdBPO47VJgESMJYAxdBYnsyNBEjATwlQDP2041htEiABYwlQDI3lydxIgAT8lADF0E87jtUmARIwlgDF0FiezI0ESMBPCVAM/bTjWG0SIAFjCVAMjeXJ3EiABPyUAMXQTzuO1SYBEjCWAMXQWJ7MjQRIwE8JUAz9tONYbRIgAWMJUAyN5cncSIAE/JQAxdBPO47VJgESMJYAxdBYnrpyKy8vl/j4eMErAwmQgLUEKIbW8m61tNDQULUhzsyZM1uNx4MkQALGE6AYGs+0TTnm5eUpIezcubOEhYW1KQ8mIgESaDsBimHb2RmaMjg4WNzN0MyZGQmQwBUJUAyviMj8CHFxcWpUiNEhRoVBQUHmF8oSSIAELiNAMbwMh28+QPxCQkJU4RDDjh07+qYiLJUEApgAxdDHnR8REdEwKkRVtFGij6vF4kkg4AhQDH3c5bhh0qVLF5k6daqykSNHKnFMS0vzcc1YPAkEFgGKoQ/7Ozw8XDp06KDmCHGprFm7du3UCNGHVWPRJBBwBCiGPupyLKzG3GBzy2gghlxr6KOOYbEBS4Bi6KOuhwhiVNjc0yYYITYnkj6qKoslgYAgQDH0QTe3NipEdSCGWHPIQAIkYB0BiqF1rBtKwh1jjPyaGxUiEu4wYz6RgQRIwDoCFEPrWLMkEiABGxOgGNq4c1g1EiAB6whQDE1kPWbMGOnevbvAGw0DCZCAvQlQDE3qn5tvvlktnsYyGVinTp1MKonZkgAJGEGAYmgExUZ5TJo06TIh1ARx1qxZjWLyIwmQgF0IUAxN6IkBAwY0K4Zjx441oTRmSQIkYAQBiqERFBvlMWfOnGbF8MHPIyTz1LlGsfmRBEjADgQohib0wsB1WdKur8vhgnaJfGv/YfJPs5Lk6i+T5J2kQqm+eMmEkpklCZBAWwlQDNtKroV0/aOypN0XifLurqOSnJws06ZNk/T0dBW79HytjI3PVcdv+XaPhGeeaCEXfk0CJGA1AYqhgcQfiTyohG5ayrFWc00qqZSHVmequL3XZEr8sTOtxudBEiAB8wlQDA1i3G+tSwg/2N26ELoXtyS7VH69KE2JIkaM+RXV7of5ngRIwEICFEMDYPdZ4xrl/T21qE25vbfrqBLE6+ckizdi2qbCmIgESKBZAhTDZrF4/mWveiH8KK1tQqiVdKzqgoyMOaxE8Y5l+2RZTql2iK8kQAIWEKAY6oD84OoDSrw+3lOsI5fLk24tqpD7f9iv8g1elyVJxysvj8BPJEACphCgGLYRa89VLiH8x17jhNC9KrjT/MsFqUoUJ27Ll5JzNe6H+Z4ESMBgAhTDNgB9IMI1cvts3/E2pPY8SZ2IvJ1UqATxZ/NSxCzh9bxGjEkCziVAMfSyb/9Yfwn7Rbq5QuhercNnqmVYdI4Sxe4rMmR13in3w3xPAiRgAAGKoRcQ712ZoQRpVkaJF6mMi7qp8LTc872rDkOjc2Rf6VnjMmdOJBDgBCiGHp4Af6gXobn7fSOE7tWcnVEiN81PUcL8l50FUlFz0f0w35MACbSBAMXQA2h3r3CNxuYdsM/jc+cvXpI3dhxRgvi/wneLHUTaA5SMQgK2JUAxvELX/H55uhKcr236HPH+U+dkyPpsVUfMZ0YXnL5Ci3iYBEigOQIUw+ao1H/3u+9cQrjw4MlWYtnj0Nr8cun23T4lili8nXP6vD0qxlqQgJ8QoBi20FFd64VlUZb9hdC9CZ/uK5Yb5u5SogjPORfrsECHgQRI4EoEKIbNEPrtMtcIa3G2fz4SV159UUK35StB7PxNmviboDfTJfyKBEwnQDFshPg/l+5VIuKEZ4N3n6iSR6Nc3nQeXJ0p24oqGrWWH0mABDQCFEONhIj8x5K90v6LRFl+qMztW/9/+/2hMtU2OJ2Fq7CjVRf8v1FsAQkYTMC2YlheXi7x8fHK8vLyDG520+z+3+I9ctWXSbLysLOE0L2lH6YWyU9mJ6l2TtfpZcc9X74nAScQsJ0YpqWlSc+ePZtsqGTmRuz//u0etT9JRK7zH3MrPlsj4+q3HsAfAEaNdgxBQUHqPMC5AJs4caLg3GAgAbMI2EoMIyIipGPHjhIcHCzuo0H8CMz6IfyfRWlyzezkgHved0dxpWi+GB+OPCgpJ6rMOse8zhd9jY208AcYFhamDOKI78w6D7yuJBM4joBtxBCXxRDCkJAQyyB3+SZN4F06Mr/csjLtVtC3WScFfwiYT3xpW76UVdf6vIozZ85UwudeEZwfEEOIIwMJmEHANmIIEezQoYPgpLcidFqYKv88d5esO2JNeVa0SU8ZWJMIQcSfw6cmuya7Uj1xLmAk2Djg/KAYNqbCz0YRsI0Y4kQ3c17QHdivFqTKv3y1Szby0TV3LJJXUS2j6rcewFrLKB+NmLt27drkXNBGi+7TJ5dVnh9IQCcBW4hhXFycugTCq9nhXxfslo7zdknMUW7P2RLr2KNnRHNgO2h9thw4da6lqIZ/r10Od+nSpeEGCt5jHpnzhYbjZoZuBGwhhrhxgvkgsy+RfxG+W342P0XwY2e4MgF46fm3+q0HXt9xRM7VXrpyIp0xtD9G7cYJXjt37qyE0ezzQ2fVmdzPCdhCDLVLIDNZ3vz1brn56xRu2O4l5AuX6mRyYoGaT/yf81Jkjsn+HCF+mDJpHCCIVt5ca1w+PzufgC3EUBsNmHWZfOP8FPnF17sFO88xtI3AwfLzDVsP3LUi3bRpBlwOwxoHfNfcTZXG8fiZBNpKwBZiiMsfjAawuNbogNHMv4bvloRiCqERbHH3XfP6ja0HcNPFyIARYOM7xjg/MG/IkaGRpJlXYwK2EENUSps37Natm0ydOlUZnjoIDw9vXGePP3f4apea89rJvYc9ZuZpxM/Tj6tpByzHwQ5+RgTcKcbcsXaFgM+rVq1Sf5L4s+SdZCMoM4+WCNhGDFFB3C3U1pjhkgiXRtoPo6UGtPQ91hBiLWFSCTdhb4mR3u/PXLgoryb8uPXAAp1OcLU/RAiiZhBBnBMUQr29xfRXImArMbxSZT09joXDeLpkV4l9HjHztO7+GG/PybOCJTgYJd73w37ZzrlZf+zGgK+z48Tw2tnJ6vEy+PJjsJbAD4dPNWw9EBJzWI6frbG2AiyNBHQQ8Hsx3LJli5w86XLN/5NZSQIPNBipMPiOwIy0IvWED0aK76Uc9V1FWDIJeEHAb8Vw9uzZct111zXMLbV/aLjAJRU3Vvei902MeuJcjUzYmqcunbH1wNLsUunevbtcddVVcvXVV8v9999vYunMmgS8J+C3YnjNNdc0CKE22f7k2Be8J8AUphJIPF4pcBHW7qHhTfqrV69eppbNzEnAGwJ+KYZRUVFNflhKEO95WP7Hl4nKkzO8Vl89y2X/NCtJcAkNL8/XKEsWzC1eN8dluOEC++ncZPlnZbvUDnM3fLVLXe5hiQ4MzzR3nJciWLv4M9j8FMGCbthN81PUUhM86T46NgYAAAc1SURBVPLzesPjf9jgHYa1jngu+pcLUtVyHzzm9quFLvvfC1PVne9O36QJRlEw3AD69SKXwcUW7P9+u0dNA2Aq4BbY4j1qNPybxXsEduuSvcqwfcFtsKV7BXu6wG5fulfgfAF2R71hB0BsLwrDtqi/W54udy5PF+wVDcPialj3Fely94oMufv7DLmn3rDWsMdKl927MkPuXblf3TzB3s2w+2ER+9UzzkERB6Td9f/SpM+uvfZab85VxiUBUwn4pRhmZWU1+WFBDP/tgUdkSlKhMqx9ezuxUCYnFsqkxAJlf9lZILC3dhbIm7AdBfLGjiPK8Oztawkuw3IR2Cvbj8jL2/OVTdyeLxO35atd5+D3D/biVlievFBvE7bkyfh6e35Lnjwfn6e8SmPfEdiYOJf9OS5XRsNic+W52MPKno09LKNgMYcF+x7DcBPimc2HlI3YfEhgT29y2fBNh+SpTTnyVHSOejJkWHSOYBH0kxtd9sTGHHliY7Y8viFbHqu3IRuy1Ybzg9dnq7u/g9ZnycB1LgtelyWwAVFZ0r/esJnUo5EH5ZHIg2p0hxFev7Uu67v2oPRdmyl91mRK73qDs1jYQ6szBRtQPbj6gPwJtuqAtO9wU5M+++lPf2rqyc3MScAbAn4phmjg7bffftmPq3379rJ+/Xpv2s64FhLQPFVrUxp4HTRokIU1YFEk0DoBvxVDNGvEiBHSqVMnueuuuyQyMrL1lvKozwn07dtX3fTCiHDw4ME+rw8rQALuBPxaDN0bwvckQAIkoIcAxVAPPaYlARJwDAGKoWO6kg0hARLQQ4BiqIce05IACTiGAMXQMV3JhpAACeghQDHUQ49pSYAEHEOAYuiYrmRDSIAE9BCgGOqhx7QkQAKOIUAxdExXsiEkQAJ6CFAM9dBjWhIgAccQoBg6pivZEBIgAT0EKIZ66DEtCZCAYwhQDB3TlWwICZCAHgIUQz30mJYESMAxBCiGjulKNoQESEAPAYqhHnpMSwIk4BgCFEPHdCUbQgIkoIcAxVAPPaYlARJwDAGKoWO6kg0hARLQQ4BiqIce05IACTiGAMXQMV3JhpAACeghQDHUQ49pSYAEHEOAYuiYrmRDSIAE9BCgGOqhx7QkQAKOIUAxdExXsiEkQAJ6CFAM9dBjWhIgAccQoBg6pivZEBIgAT0EKIZ66DEtCZCAYwhQDB3TlWwICZCAHgIUQz30mJYESMAxBCiGjulKNoQESEAPAYqhHnpMSwIk4BgCFEPHdCUbQgIkoIcAxVAPPaYlARJwDAGKoWO6kg0hARLQQ4BiqIce05IACTiGAMXQMV3JhpAACeghQDHUQ49pSYAEHEOAYuiYrmRDSIAE9BCgGOqhx7QkQAKOIUAxdExXsiEkQAJ6CFAM9dBjWhIgAccQoBg6pivZEBIgAT0EKIZ66DEtCZCAYwhQDB3TlWwICZCAHgIUQz30mJYESMAxBCiGjulKNoQESEAPAYqhHnpMSwIk4BgCFEPHdCUbQgIkoIcAxVAPPaYlARJwDAGKoWO6kg0hARLQQ4BiqIce05IACTiGAMXQMV3JhpAACeghQDHUQ49pSYAEHEOAYuiYrmRDSIAE9BCgGOqhx7QkQAKOIUAxdExXsiEkQAJ6CFAM9dBjWhIgAccQsFwMy8vLpWfPng02cOBAWbBggWOAsiEkQAL+ScByMYyIiJB27dpJWFiYspCQEOnQoYOEhob6J0HWmgRIwBEELBdDiGDnzp0vg4fvIJAMJEACJOArApYrUFBQkAQHB1/W3ri4OCWGuIRmIAESIAFfELBcDHFJjJGge8AlMr5nIAESIAFfEbBUDPPy8tQIECNBLYSHh6vvOGeoEeErCZCALwhYKoaa8Gl3kzFPCKMQ+qLrWSYJkIA7AUvFEKKHmye4TJ45c6ZghMh5Qvfu4HsSIAFfEbBUDHHzBEtpGEiABEjAbgQsFUNcEuNSmYEESIAE7EbAMjFMS0tT84N4ZSABEiABuxGwTAwxR8iF1XbrftaHBEhAI2CZGGoF8pUESIAE7EiAYmjHXmGdSIAELCdAMbQcOQskARKwIwFDxLCurk7Gjx8vP//5z+XWW2+VGTNm2LGtrBMJkAAJtEjAEDHE2kHtaRLtdf78+S0WygMkQAIkYDcCusWwtra2iRBCEPv162e3trI+JEACJNAiAd1iiEtkbTTo/tq/f/8WC+UBEiABErAbAd1iiAaNGzeuiSAuXrzYbm1lfUiABEigRQKGiCFynzRpkvzmN7+RHj16yLx581oskAdIgARIwI4EDBNDOzaOdSIBEiABTwlQDD0lxXgkQAKOJkAxdHT3snEkQAKeEqAYekqK8UiABBxNgGLo6O5l40iABDwlQDH0lBTjkQAJOJoAxdDR3cvGkQAJeEqAYugpKcYjARJwNAGKoaO7l40jARLwlADF0FNSjEcCJOBoAhRDR3cvG0cCJOApgf8PyaAt7shVtXEAAAAASUVORK5CYII=[/img][br][br]Jada claims that all the segments in [math]ABC[/math] are parallel to the corresponding segments in [math]A'B'C'[/math]. Write Jada's claim as a conjecture.
Prove your conjecture.[br]
In Jada’s diagram the scale factor was greater than one. Would your proof have to change if the scale factor was less than one?[br]
IM Geo.3.4 Practice: Dilating Lines and Angles
[size=150]Angle [math]ABC[/math] is taken by a dilation with center [math]P[/math] and scale factor 3 to angle [math]A'B'C'[/math]. [br]The measure of angle [math]ABC[/math] is [math]21°[/math]. What is the measure of angle [math]A'B'C'[/math]?[/size]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAXUAAAEbCAYAAAAlAxTiAAAgAElEQVR4Ae1dB7gUNRcVFAvVhljoHRSpIl0UBJSOFBWVpiBVQUU6CtilWVFQ6b+CWKkqXUVBRZoFu3QUsGIBzf+daHDYN/ve7E5mJrlz833v231TkpuTzJm7mTvnHiO4MAKMACPACJBB4BgyPeGOMAKMACPACAgmdZ4EjAAjwAgQQoBJndBgclcYAUaAEWBS5zlgJQIXXXSRaNiwoZW2s9F6ERg9erQ45phjRMeOHfVWbGltTOqWDlzczc6ZM6cYPHhw3GGIff/79+8vCb1v374ksPj1119994NJ3TeEXEHYCKxfv15eyPPmzQu7aW7PIASuu+46OQ/uuOMOg6xK35Rvv/1WXHjhhelX8O+ZTOq+IeQKwkZg8uTJ8mLGRcAlfggcPHhQNG3aVM6Bhx9+mAQAcFRKliwp8uXL57s/TOq+IeQKwkage/fuolChQmE3y+0ZgMC2bdtEjRo1JKHPnj3bAIv8m/DGG2+IU045RRQvXly8//77vitkUvcNIVcQNgJVqlQRrVu3DrtZbi9iBD788ENRqlQpkTdvXrFkyZKIrdHT/HPPPSdvUBdccIH4+uuvtVTKpK4FRq4kLAR+++03eRHcfffdYTXJ7RiAwNKlS8Wpp54qihUrJtatW2eARf5NeOyxx+RcbtKkifj555/9V/hvDUzq2qDkisJAYNWqVfJCeO2118JojtswAIE5c+bIMa9WrZr48ssvDbDIvwlBhmEyqfsfH64hRATGjRsnL/ADBw6E2Co3FRUCjz/+uBzvxo0bix9//DEqM7S2q8Iw+/Xrp7VeVRmTukKCP61A4KqrrhLly5e3wlY20h8CY8aMkYSOMadSwgjDZFKnMlti0g88KMOFwYU2AgMGDJCE3qdPHxIdDTMMk0mdxJSJRyf27t0rL3QqscnxGLXUe9mpUyc5ziNHjkz9ZAPPCDsMk0ndwEnAJrkjsGDBAnmxr1mzxv0A3mo1AohsatasmRzjhx56yOq+KOOjCMNkUlfo86fxCNx5550ie/bs4vDhw8bbygamhsD27dtFzZo1JaHPmjUrtZMNPdoZhvnee++FZiWTemhQc0N+EYAXp0Mbw68dfL5eBDZs2CBKly4t8uTJIxYvXqy38ohqc4ZhfvXVV6FawaQeKtzcmB8EzjzzTNG7d28/VfC5hiGwbNkycdppp4miRYuKtWvXGmZdeuY4wzB/+umn9CrxcVbapP7LL7/4aJZPZQRSQ+CLL76QP82nTp2a2ol8tLEIzJ07V2TLlk1UrVpVYHwplLvuukvO06uvvjqy7qRN6rizsvRpZOMWu4afffZZebFs3rw5dn2n2OFJkybJ8WzUqJH44YcfSHRRhWFGre2eNqnXq1dPDkqPHj0Ee+0k5qTRnbj11lu1yJIa3cmYGKe82SuvvJJMj00Kw0yb1DEa6o0veO0vvPACmQHijpiHAKevM29M0rHolltukc4glWcjJoZh+iJ1DCoU0+rWrXvEa9eRjimdycLn0EYgV65cYtCgQbQ7Sbx3nTt3ljwxYsQIEj01NQzTN6mr0WGvXSHBn7oRwAscSCzMz3B0IxtOfb///rto3ry5HMOJEyeG02jArZgchqmN1IEhe+0Bz6SYVq/S133zzTcxRcDebu/YsUPUqlVLEvrMmTPt7YjDcmcYpona7lpJXfVbee0QtOe1doUKf6aLAB7GFyxYMN3T+byIENi4caMoU6aMyJ07t1i0aFFEVuhtFmGY+NWIMExTtd0DIXXAiBcJ1Fr7jTfeKHitXe/kilNtnL7OvtFevny5OP3000WRIkXEu+++a18HXCx2hmGarO0eGKkrTFSGD/baFSL8mQoCKn0dwuC42IHA888/LzV6cDP+/PPP7TA6CyuRPhEeug3a7oGTOrBirz2LGcO7kyKwevVqeTFx+rqkEBm144knnpDjdemllwoq2alsC8MMhdTVrHN67S+++KLazJ+MQFIEVPq6/fv3Jz2Gd5iBwD333CMJvUOHDmYYpMEKG8MwQyV1YAyvvU6dOnLwsdaOjCBcGIFkCEBDo1y5csl283ZDEMAbv1ie6NWrlyEW+TPD5jDM0EldQc1eu0KCPzNDgNPXZYaOGfu6dOkiCX348OFmGOTTCtvDMCMjdeCOp+LstfucgYRPV+nrqGTBoTZUf/zxh2jRooUk9AkTJpDoHoUwzEhJXc0C5bUXL15c8Fq7QoU/Fy5cKAmD09eZNxd27twpateuLcdnxowZ5hmYhkXOMEybtd2NIHXg7/Tae/bsyWvtaUxKaqeo9HWHDh2i1jWr+7Np0yZRtmxZAT0e5I2lUBCGCW13hGHaru1uDKmriTFq1Ch592evXSES30/ohVSvXj2+ABjY8xUrVogzzjhDFC5cWLzzzjsGWpi6Sc4wTAra7saROoYEXrv6aQevHS+gcIkfApy+zqwxh6DascceKypXriw+++wzs4xL0xoVhklJ291IUlfj4/TaX3rpJbWZP2OAgEpf98wzz8Sgt+Z38cknn5S/oBs2bCiovDNALQxTzSKjSR1Gsteuhipen88995wkEU5fF/2433vvvXIs2rdvH70xmiygFobphMV4UlfGBum1f/XVV+KOO+4QeHsMoVlUXm9W2Nn4yenrzBi12267TRI6lkEpFIphmInjYg2pw3A8mNG91o6f93gTDjkGR44cKSpWrCgqVarExJ44U0L+v379+qJBgwYht8rNORHo2rWrvDaGDRvm3Gztd4phmG6DYRWpqw4or71EiRLCz1o7PHQQunPdFl46to0fP141x58RIMDp6yIA/d8m//zzT9GyZUtS14EzDBPvP1AuVpI6BsTptUNvIp0IGXjn8MwTC5Icw2vnEg0CKn0dYoe5hIvArl27jrzlPX369HAbD6g1hGHmz59fhmHiGR31Yi2pq4HBCyrwrOG1v/zyy2qzp898+fK5kjeTuif4AjtoypQpckw5fV1gELtWjIfSEE/LmTOnmD9/vusxtm1EGGb27NllGCYVbfesxsB6UkcH4bWrPIjw2qGw5qXgZoBXgxNL4pJM4n7+P1gEOH1dsPi61b5y5UpRoEABUahQIUFFlkHltqUUhuk2donbSJC66lSqXjvIO1FrRj045QgYhWr4n8j/2KpVq/AbjmmLyCN83HHHyQCBrVu3kkBBhWFS0nb3OjCkSB2dTsVrR/5EJ3ngwenJJ5/suiTjFVA+zh8C+JWFmy2Sl3MJHgHlzV5yySVi3759wTcYQgvUwjBThYwcqSsAvHjt69evF1hXRwgjQuhA6Hh4yiU6BFT6uiVLlkRnRExavu++++QNtF27dmR6TC0MM52BIUvqAANrg1mttWOZBUswCGEEyXOJFgGMAzx1Kq+iR4tm8tYHDhwocUb2MQqFYhhmuuNCmtQVKMprL1myZMoRMqoO/gwHAU5fFzzO3bp1k4Q+dOjQ4BsLoQWKYZh+YIsFqQMgp9feu3dvzxEyfsDlc1NHoHTp0uLaa69N/UQ+I0sEoEuPZ0j4JYSE3hSKMwyTira733GJDakroKDxgkkNr/2VV15Rm/nTAAS+++47OTYTJ040wBpaJuzevVvUrVtX4jtt2jQSnUMYJrTdEYaJAAku/yAQO1JHt+G116xZU05weO0Q+eESPQKLFi2SY/L2229HbwwhC7Zs2SLKly8vTjrpJPHqq6+S6JkzDJOKtruugYklqSvw2GtXSJjxCU0fpBTj9HX6xmPVqlUCyUYKFiwoqNws1RvHEHyjEoapb8SFiDWpA0j22nVOJ391cfo6f/glno2orhw5ckh9o08//TRxt5X/qzBMStruugci9qSuAGWvXSER3edZZ50lIPPAxT8CTz31lFzKuvjii8X333/vv0IDaqAWhhkUpEzqDmTx85TX2h2AhPj1yy+/lCT09NNPh9gqzabuv/9+iWXbtm3JdJBaGGaQA8Ok7oIuZHcRIVOqVCmOkHHBJ4hNc+bMkZhD95pL+gjcfvvtEkeIolEoFMMwgx4XJvUkCDu99j59+nCETBKcdG2GXkfevHl1VRfLeq6//npJ6EOGDCHRf4phmGEMDJN6Fig7vXYq4WBZdFnrbsgw4NX/rDJJQXsHolJcUkfg8OHDonXr1pLQx44dm3oFBp7hDMOkou0eFsxM6h6Qhtdeo0YNedHAa4fOBBdvCCAtGtQvoVvvpl2vasmdO7fA0gH1An0hJeuM6JTEdIzAaOrUqUeOyQqPPXv2iHr16sm5ifOiLBhn/KGgn7BH/Z+KXQjDhLY7wjARncYlNQSY1FPAi732FMASQpK4Ur105oFNrGXDhg2SlObOnZu4i9z/eFYDMocyKDJsQSUUv1JA9NiG9IqQhIZiqCL/ZCB89NFH4txzzxUnnniiEc9+VMYwlSYSfVH9TdaHxO3OMEwq2u6JfQz6fyb1FBFmr907YLjIlfJlZqSuwu++/vpr75VbeCSwAMmBtBUuIDFsA6GrXzIgc2xT/7t1FRLFCAE955xzxFtvveV2SOjbcIPCzci51AZiVzf2rAxS8wDLcFTCMLPqcxD7mdTTRFV57RCg4rX2jCDiZzfICwXfMyMoyL+CnKgXlVXLeYMDLiBwzCdVsiJ1LNkcf/zx4vzzzxeffPKJOi3ST3XDSiRw3NgTt7kZSjEM062fYWxjUveBMjwkXmt3BxAkddNNN8mdTsJyOxrp67D2Tr0AD3WjU31V+vHOpRZF9G7r0Yjjx00ASzYQQDOlqBtWos3w3p2eu5u91MIw3foY5jYmdQ1ojxgxQl5o7LX/ByY8NCwt4GJ3EtZ/R/zzDWJqIKk4pK/DUoS60SkccDMDVs6Cm2Ai+WP/Aw88ILG64oorxN9//+08JfLv6Bf65yzKe8/sVxq1MExn/6P6zqSuCXmn1963b9/YR8iAqOGhqbXjZDC/+eabkqgWL16c7BAy24EJbnTOAvJO/CUDok/85TJo0CCJU/fu3Z2nG/Pd7YalvHc3IymGYbr1M4ptTOqaUXd67XGOr3UjMDeoJ0yYIMmKutqe25JKsrVzLFk4if6GG26QGA0ePNgNQiO2YbydzwpgFLz3xF8h2G5SGKYR4Gk2gkldM6CoDl77hRdeKC9EeO1xk5KFd+52MbtB3bFjR1G2bFm3XaS24VcLyNpZVOSLc3kKa9IgSNwE/vrrL9GmTRv5/4MPPug81ajvbjcsGOjmvTvDMDnAIJhhZFIPBldZaxy9dhA6yCqR1J3E5YQczyGuueYa5yaS3+F5J66nw7NNXGZRN8S9e/dKDEHwpoucuY03BhFzwLnchDBMaLsj0gmhwVyCQYBJPRhcj9QaV68dZKWIHOTltraOWGSQFqevOzJd5JePP/5YVKhQQZxwwglkEqWbGIZ5NOp0/mNSD2kslddepkwZEYe1dhA6lhzgqSlyT4Rapa/DjY/LPwjgwfHZZ58t//CdQlFhmNB2NykMkwK2bn1gUndDJaBtuEjjvNaeCOvo0aOlp85aOv8g8/LLL0vvHF46vHUKxeQwTAr4uvWBSd0NlYC3DR8+XJJZXLz2ZHC2aNFCXHDBBcl2x2q7Cv/DOjTW0ykU08MwKWDs1gcmdTdUQtjm9Nr79esXuwgZQAztkp49e4aAttlNILIFzxYQ6YKIFwrFhjBMCji79YFJ3Q2VELc5vfYFCxaE2HK0TanQPdMjO4JGCbHnIHSQIIViSxgmBayT9YFJPRkyIW6H1169enV5ccNrx9t21ItKX7dx40bqXU3aP7wdCkLHMgWF4gzDTHwRiUL/bOkDk7pBIxUnrx2Z4fPkyWMQ+uGZAt0W6LeA0PEgkULBg93zzjtPPuh95ZVXKHTJ2j4wqRs2dHHx2hHeFsf0dQjpg8IiCB364RQK5iyejyAUk8NTox9RJvXox8DVAuW14xV6imvtSF8Hbz1OBdrn0ECHFnpiGjtbcaAYhmnrWCi7mdQVEgZ+4rVqimvtWEeHpxqH9HVqWsGDxevx8GgxrhSKCsPELw8qYZgUxoVJ3YJRHDZsmCRBKl67SluWmFDBgqFIy0SsMSOPKPKJQtCKQqEYhklhXNAHJnVLRhLeHV7UgYcLYSib45kRm4711ziUqVOnyjGrV6+elJyl0GdqYZgUxsTZByZ1JxoWfHd67QsXLrTA4owmVqtWLYM6Ycaj7N8yduxYSeitW7cmE6ZKLQzT/lmWsQdM6hkxMX6LzV67Sl8H3RfKZciQIZLQka6NQqEYhklhXNz6wKTuhool22z02vHAEEtIlNPX9ejRQ/YRCZUpFGcYZtzfALZhPJnUbRilTGxctWqVVWvtKn0dtNQplrZt20pCv//++0l0D2GYUI1EGCbCF7mYjwCTuvlj5MlC5bWXK1dOmLzWjixHUKekVnCTwgtV+BUyZcoUEt1zhmHiBSMudiDApG7HOHmy0um133zzzUZGyIDQqaWv+/TTT2U+zhw5chyVvs3ToBl6EPKHIgwTr/5TCcM0FGrtZjGpa4c0+gqHDh0qPUZ47cguZEpR6euwBEOlINdmwYIFZe5N3FQpFBWGCW33PXv2UOhSrPrApE50uEEwCB3EcgC8dkQvRF3wcBT2UNEHgTd70kknifLly4stW7ZEDa+W9imGYWoBxqJKmNQtGqx0TDXJa1fp6xDWaHuZNm2avEHVrVtX7N692/buSPuphWGSGJQ0OsGkngZotp1iitfesmVL+evBNvwS7R03bpwk9FatWgkq+VWphWEmjlmc/mdSj9FoR+21QxrA9vR1CsNu3bqRmTnUwjDJDEyaHWFSTxM4W09buXJlJGvtKn2dzRriN954o/TQqUgGO8MwbR4XW6/FoOxmUg8KWcPrVR4nHvKFESEDmV08JLU1fV27du2k/ffdd5/hI+vNPIRhQtsdYZhUtN299Zz+UUzq9Mc4aQ+dXnv//v0DjZCxNX3dvn37ZIYm3JAmT56cFEubdlAMw7QJ/6BtZVIPGmEL6ldRD/Dag9JkQeo6vHFpU9m6dauoVKmSOO6448QLL7xgk+lJbZ0/f74Mw4S2O5UwzKSdjekOJvWYDnxit+G1V61aVS4xwGvXXZBk2qa16DVr1ohChQqJAgUKCGBDoagwTGi7UwnDpDAuzj7oeJ+ESd2JKH8XQXjtKn3dnDlzrEAYOWFz5swp8Ebu5s2brbA5KyOdYZiHDh3K6nDeHwECSg3Tb9NM6n4RJHi+bq8dcq1Yk7Yhfd306dOlrXXq1BG7du0iMbrqoTilMEwSA+PohFLDPOGEExxb0/vKpJ4ebrE4S5fXbkv6uvHjx0tCx0tSFN56xSSlFoZJ8cKDbAbe4UBSch1qmEzqFGeJxj6tWLHC91o7cqu2aNFCo1X6q1LSxV27dtVfeUQ1UgvDjAjGQJtFUnJ451DD/Pjjj7W0xaSuBUb6lahkw4iaSCVCBq/RY+nF5PR1+CUBG2+77TYSA+kMw6Si7U5iYBI68cwzz8h5BzXMvXv3JuxN/18m9fSxi92ZTq99wIABnvqv0teF8YKTJ4MSDmrfvr28sO65556EPXb+izDMihUryjDMF1980c5OGGQ1luLWr18vdfLr168v8KdDOvrBBx+U865Nmzba8x4wqRs0gWwxxem1L1myJFOzJ06cKCevaenr9u/fLxo2bChte/LJJzPtgy07KYZhRon9gQMH5Pzo1KmTgDeNm6R67rJ8+fK0TVPXzw033JB2HZmdyKSeGTq8LykC8NqrVKkiJ31mXruJ6es+++wzUblyZXHssceKefPmJe2jTTtUGCZeIKMShhk1/iBuLMuB0J2lSJEiYuTIkc5Nnr8rNcxBgwZ5PifVA5nUU0WMjz8KAeV1YK3dzWsvW7as6Nix41HnRPnPO++8IwoXLizOOOMMgRsThaLCMKHtTiUM04RxAXG7heKC5NMh9bDUMJnUTZg9ltuQzGvHAztcFDrWIHVAhITcuXLlErjRbNq0SUeVkdehlgOw9ktF2z1yUP81AJjiL7FgTqdC6mGrYTKpJ44Y/582Aoleu0pfpyP2Nm2j/j1xxowZ8gZTu3ZtsXPnTr/VGXE+xTBMI4D914h8+fJlIG88NAWpe11TV2qYxx9/fGhqmEzqJs0iArZgsqu1dhAoLoCoX+TBLwXYgVj533//nQDKQiYbQZ+ohGGaNihK/z/RI8dDU6ypeylQwzznnHNkUvLVq1d7OUXLMUzqWmDkShIRwIMgkA4SM7uttSceH9T/w4cPl3Z06dIlqCZCr1eFYd57772htx2XBhHpAk/d+ZBUxZV7CRVFUvITTzxR4FnTRx99FCpsTOqhwh2vxk4//XSBP5D7LbfcEnrne/XqJdu+9dZbQ287iAYRhtmgQQPZJyra7kHgpKNOeOgg9JtuukmcfPLJomjRopLkQexZlalTp8oxghrmnj17sjpc+34mde2QcoVA4Ouvv5YTG2nSlNeOV6Ffe+21UADq0KGDbP/uu+8Opb2gG0EYJrTdEYZJRds9aMz81K8IHXVgHR3Liohbz6qMHTtWzrvWrVuLw4cPZ3V4IPuZ1AOBlStV6es2bNggwcBFgdjwoL12XHiXXnqpbOeJJ54gMRAUwzBNHxjMUy9eubMfSgDv+uuvd24O/TuTeuiQx6PB22+/XeTOnTtDZ4P02j///HP5kDZ79uzi+eefz9C2jRtUGCa03amEYZo+DirCBZ9ei0lqmEzqXkeNj0sJgczS1wXhtb/77rsyKgFr+KifQqEYhmnDuKgHol5tNU0Nk0nd68jxcSkhkDdv3izD7XR57RALw6+CMmXKCGRZolCcYZhRh4RSwDOVPiCc0YuXbqoaJpN6KqPNx3pCAMsEWJP0kr5u2bJlvtbaZ86cKduqVauW2LFjhyf7TD+IYhim6Zinap9Sw8yRI4cU+kr1/CCPZ1IPEt2Y1q3S13355ZeeEcAaPG4EFSpU8BwhoxQgmzdvLn777TfPbZl8ILUwTJOxTtc2qGEWLFhQJiVftWpVutUEdh6TemDQxrdiEBNSc6VanF57VrHlI0aMkDeBzp07p9qMscerMEwq2u7GAu3DsPnz58sX6qCGuWXLFh81BXcqk3pw2Ma2Zr/p65xe++uvv54Bx969e0tCj+KFpgzGaNiAMExq2u4aYDGuimnTpsl5BzXM3bt3G2efMohJXSHBn1oQgFJgtmzZxKhRo3zVB68dL9tgScbptV955ZVy21133eWrflNOphiGaQq2Ou0YN26cnHetWrUShw4d0lm19rqY1LVDGu8KIWIEItaVvk557dDQqFq1qqx70qRJJEBeu3atDMPMnz8/mTBMEgOT0ImhQ4fKedetW7eEPWb+y6Ru5rhYa5V6ePndd99p6wMiXHLmzCkvLCgtUigqDBPa7lTCMCmMS2IfbExKzqSeOIr8vy8Err32WlG6dGlfdThPhjcLMaXTTjtNqKWX888/X7ittTvPM/k7xTBMk/FO1zZb1TCZ1NMdcT7PFQGd6euQZCNPnjzyJqE0ZJYuXeq61u5qjIEb1S8ZhGFS0XY3EGZfJtmuhsmk7mv4+WQnAip9HVKs+S2zZs2Syy01a9YU27Zty1DdwIED5X6bvHaKYZgZBsbyDRTUMJnULZ+EJpmPZBh4SOo3fd1DDz0k62nWrJk4ePBg0i7Ca69YsaI81vQMQNTCMJMOisU7oIZZqFAhmZR85cqV1vaESd3aoTPP8DFjxkiC9bOsgOQEuDEgbZjX4vTa33jjDa+nhXacehZARds9NOBCbGjBggXyYTzUMDdv3hxiy/qbYlLXj2lsa0QML8IO0y19+vSRhD5gwICUqzDRa//hhx/IabunPDAWnDB9+nQ57+rUqSN27dplgcWZm8iknjk+vDcFBJBkF7rS6ZSrrrpKXljw9v0UU7z2L774Qt7g8CIWEoZwMRMBPP/BL8OWLVtGniBdF0JM6rqQjHk9Kn3dlClTUkLixx9/FI0bN5YX1uOPP57SuckOxhJMlGvt69atk2GY0HbHm7FczERAqWF27drVTAPTtIpJPU3g+LSjEUCmIXg8KvTw6L3u/0HFsVq1avI8LzK97rUk36q8dhB8WGvtKgwT2u6pYJG8F7wnCAQoq2EyqQcxY2JYZ7L0dcmgeO+990SxYsXEqaeeKrAeHlRxeu0g+SCLMwxz+/btQTbFdftAgLoaJpO6j8nBp/6HQIMGDUT9+vX/25DJN4Q+IjNSqVKlxIcffpjJkfp2IeQRvyTgtQdxE3GGYVLRdteHvhk1xUUNk0ndjPlmvRVe0tehk7Nnz5bkWqNGDfHtt9+G2m947XhZCeSu02tPJwwz1I5zYwJqmJUrVxZISj5v3jzSiDCpkx7ecDqn0tc999xzmTb48MMPS0Jt2rSp+PXXXzM9NsidOr12P2GYQfaR6/4PASQlL1y4sIAa5ooVK/7bQfQbkzrRgQ2zWyr7OsL4kpU77rhDEvp1112X7JBQt+vw2lUYJhVt91AHIKTGFi5cKHLlyiWgSQTnIw6FST0OoxxwH7NKX9e3b19J6DfffHPAlqRefTpeO8IwGzVqJPtERds9deTMP2PGjBlyjGrXri127txpvsGaLGRS1wRknKupXr26gOqgW+nYsaO8sEaPHu2224htkPH1utYedBimEYAQMGLChAly3kF/349shY1QMKnbOGoG2YzUXnhr8s477zzKqp9++kk0adJEXliPPfbYUftM/Ud57Uij5xYho8Iwoe3utt/UfsXNLqWG2aVLl7h1XfaXST2Ww66v0yp9HdYuVfnqq68Ekk8jyiSrh6fqHFM+nV47Yu9VUWGYSAASVhimaps/vSPAaphCMKl7ny98pAsCKj577969cu/7778vihcvLk455ZTQ3uJ0Mcv3JiS7xk0JXrvKUYkwTDdtd9+NcQVaEGA1zH9gZFLXMp3iW4kzfd1rr70m8uXLJ0qWLCnWr19vPSjw2s8++2xJ7iVKlMhU2936zlrcAVbDPHrwmNSPxoP/SxEB6E9fffXV4n//+3WXtPUAABrtSURBVJ8kvwsvvFB88803KdZi5uEqDPPcc8894rWzQJdZY4Uw2ipVqsjnOtAf4sLLLzwHfCCAXI5Yorjiiivk5+WXXy5++eUXHzWac6oKw+zfv780Cl57hQoVZD+da+3mWBw/S5CUvEiRIgJqmMuXL48fAEl6zJ56EmB4c9YIqPR1IHYsw1Ap+OWBPrlpuzvX2tlrj27EFy1aJHLnzi2ghrlx48boDDGwZSZ1AwfFFpOQFBrkh1flKRSEYXrRdsezA/baoxvxmTNnynlXq1YtsWPHjugMMbRlJnVDB8Z0s6655hp5YeFBIoWSThim8tohFMVeezizYOLEiXLe4WU3VsN0x5xJ3R0X3poEgZ9//llcdtll8sI6+eSTRY8ePZIcac9mFYYJbfdUk2k4vfZBgwbZ02kLLVVqmJ07d7bQ+vBMZlIPD2vrW0LKOkgCYMnlkUcekZ+TJ0+2ul8qDBPa7n7CMG+55RaJB7x2fminf0qwGqZ3TJnUvWMV6yM/+OADgVhteOeIBFHp62x+u9IZhqlD2x03iPPOO0+SO3vt+i4XVsNMDUsm9dTwiuXRIHGQOUgd5I4C0oKkqa1F/dJAGKZubXf22vXMClbDTA9HJvX0cIvNWc8++6z0PLHsguUXVVJJX6fOMeUT4mNBh2Gy1+5vtKGGWbVqVTlOc+fO9VdZzM5mUo/ZgKfS3UcffVReVHgwigekzgI5AER/2Fb69esn+xSWtjt77anPkHXr1omiRYsKqGFyVFHq+DGpp45ZLM4YNWqUJD+ELiaWzZs3y33w4m0qUWm74yUtXmv3NlMWL14s8uTJI6CGuWHDBm8n8VFHIcCkfhQc/A8QuOmmmyRpw6t1K17S17mdF9U2Zxgmfn1EVQYMGCBxhVYJR8hkHIVZs2ZJfPBSG6thZsTH6xYmda9IxeQ4vO6P9ebEpBfO7kOz+swzz3RuMvY7xMVUGKYJvyycXvvgwYONxS1sw5SEc7NmzVgN0yf4TOo+AaRyOoS4EAmiYtAz6xdIEhef6UWFYULbHRE8JhWn1x6HDPeZYa/UMDt16pTZYbzPIwJM6h6BonwYvFlI5oLQEbudWUH6uuzZs2fqyWd2flj7VBgmtN1VGGZYbXttB167kvWNq9eeqIbpFTs+LjkCTOrJsYnFHrxFCeJDNAvC8LIqa9askeS/YMGCrA6NbL8zDNMGbfe4eu2ZqWFGNnkINMykTmAQ0+0CdE6wNIH0c9A/8VLU2qdKX+flnDCPcYZh2qTtHiev3asaZpjzhlJbTOqURjOFviAhNJZbkCAaCoVey3XXXSegk2JiySwM00R73Wyi7rVjrlWrVk3OvTlz5rhBwNt8IsCk7hNAG09/7LHH5EXVpEkTAa8plYL0ddDiMK2oMEx82l4Qq01xrf29994TxYoVE1DDXLp0qe3DZKz9TOrGDk0who0ePVoSOl7ESbWo9HXjxo1L9dRAj1fa7vDUKRWk0sOvKbwub3uEDJaX8ubNK3/l2SwCZ8P8YlK3YZQ02YhX40ESiDhIp+BBKs5ftWpVOqdrPyeVMEztjYdUodNrHzJkSEit6m1m9uzZct7UqFFD6FDD1GsdvdqY1OmNqWuPsBYOQkZMcLrlrrvuknWYkHEG5OA1DDPd/pp0ntNrX7lypUmmZWrLww8/LOdM06ZNtathZtpwjHcyqRMffMjK4oICoeMC81Nat24t8Ip71EWFYUIO2EsYZtT26mofXnv58uXlWNrgtSs1TDgUXMJDgEk9PKxDbwn6GfjJC0LHT2C/pWDBgqJ79+5+q/F1fjphmL4aNOzkv//+W9jgtYethmnYMEVqDpN6pPAH1zgeRiH0EA+n8JDKb8FLPLg5RJm+zhmG6dR299s3G8832WuPSg3TxnEMwmYm9SBQjbhOhIshbAzhY9Cm1lHmzZsnSd1PHk8/djjDMBO13f3Ua/O5pnntGBeEyeLmj/HiEg0CTOrR4B5Yq3ihAxcVXvBA9hhdBenrcubMqau6lOrxE4aZUkOWHrxo0aLI19rxywkvsmHu4RcVl+gQYFKPDnvtLT/++OPyomrcuLFAfkedpWHDhuKiiy7SWaWnulQYZjJtd0+VxOAgeO0KK9zQw4yQgcQEpCYgOYFnHlyiRYBJPVr8tbU+ZswYSehBve0JwS+kZguzeNF2D9MeG9qC1463fuExDx06NHCTEX2EuQFRuKiW5gLvpGUNMKlbNmBu5iq9kD59+rjt9r0t7PR1OsMwfXfewgoSvfagXhaDTDNuHnhfwAY1TAuHMi2TmdTTgs2ck5BYABfWyJEjAzNq6tSpso3PP/88sDZUxbrDMFW9cfwM0mtXaphIrGKTGmYc5gGTuqWjfPDgQZl9CIQOOdwgC9LXFShQIMgmZN0qDBM/53WEYQZusAUN/PXXX0ettevw2imoYVowdGmbyKSeNnTRnbh9+3aB5LwgdCTrDbrg53XQ6eucYZhQ8+OiFwFdXjslNUy9CJtTG5O6OWPhyZINGzaI0qVLizx58gi8gBJ0OXz4sExf50czJisbnWGYqWi7Z1Uv7z8aAb9eO1U1zKNRsv8/JnWLxnDZsmXitNNOE0WLFhVr164NxfKg09c5wzBT1XYPBQCCjSxcuPBIhMywYcOy7CHWzC+77DL5yxBr6VzMRoBJ3ezxOWLd3LlzRbZs2aS29hdffHFke9BflMrenj17tDelwjCRq5JLuAjAa1dLKXhpaPXq1a4GIKqlevXqktCR+5WL+QgwqZs/RmLSpEnyomrUqJH44YcfQrUYCnuIQdZdlChVutruuu2Ja33w2suWLSvnV6LX/sEHH4gSJUoIqGG+/vrrcYXIun4zqRs+ZErD/Morr4zEUki96n6hSYe2eyRgEG3UzWsHiYPMQepek5IThce6bjGpGzxkeIMTES4IKYyiHDhwQLY/duxYLc2HGYapxeCYVeL02jHvsOwSdzVMG6cAk7qho9a5c2dJqCNGjIjMQp3p68IOw4wMNMsbfuSRR+S8A6kjN2qytXbLu0nafCZ1w4YXqeKaN28uL6yJEydGat3dd98t7YCH7aeoMExou4cRhunH1jif61TDXLBgQdK19jhjZEPfmdQNGqUdO3aIWrVqSSKdOXNm5JYhfV3lypV92eEMw9Sl7e7LID7ZFQGl8OhUw8Q7CipCBksx7LW7QmfcRiZ1Q4Zk48aNokyZMiJ37twCb/+ZUAoVKuQrfR3CMNXPeJ3a7iZgQ8mGrNQwnV778OHDKXWdZF+Y1A0Y1uXLl4vTTz9dFClSRLz77rsGWCTEt99+Kwn5ySefTMseZximbm33tAzikzIgADVMCHLhxou19MwKvHaVdxRe+5tvvpnZ4bwvQgSY1CMEH00///zz8jX8KlWqiDBUEL1210/6OhWGqTsU0qvtfFzWCOCmDU0fEDokdL0WeO34RYnz2Gv3ilq4xzGph4v3Ua098cQT8uK49NJLBcIHTSqDBw9OK31d0NruJmFkqy1IZoEXyqCGiQinVAt77akiFu7xTOrh4n2kNRVZ0qFDhyPbTPqC9HX16tVLySQVhhmktntKBvHBGRBAujmknUP6Ob9qmOy1Z4DXiA1M6hEMw6233io99F69ekXQurcm8Tah1/R1v//+uzFhmN56F8+jkBAayybQetGlhnno0CFeazdsOjGphzwgXbp0MX49csuWLdJGL2utpoVhhjyc1jSn1DCbNGkiglDDnD9/Pq+1GzIbmNRDGgh4sy1atJBkOWHChJBaTa8Zr+nrVBgmtN1NCcNMr8e0zwpLDdPpteMhLEfIRDOvmNRDwH3nzp2idu3aktBnzJgRQov+mkAC66zS1znDMMPSdvfXq3ieHYUaptNrj1LmIp4jLgSTesAjv2nTJvm6da5cuQQeLNlQ4GU1bdo0qakIw4S2O8Iww9R2T2oQ73BFIEo1THjtkFXGGj7m01tvveVqI2/UjwCTun5Mj9S4YsUKccYZZ4jChQuLd95558h2k79AhvXYY48VydLXOcMww9Z2Nxk3k2yDVg9uyiBUJDmJssBrR/pF2MJeezgjwaQeEM54eQfkCO2Uzz77LKBW9FeLmw8uQFyMiUWFYUal7Z5oD/+fEYFt27aJGjVqyDGcPXt2xgMi2MJee7igM6kHgDderQcxItZ7//79AbQQXJXJ0tdFre0eXI/p1Pzhhx+KUqVKCahhLlmyxLiOsdcezpAwqWvG+Z577pGE3r59e801h1Ndp06dMqSvU2GY/PM5nDFIp5WlS5eKU089VRQrVkyYrIb5559/8lp7OgOcwjlM6imAldWht912myT0nj17ZnWosfuRvk4tr/zxxx/WhGEaC2gIhs2ZM0fOu2rVqglb1DBfffVVXmsPaG4wqWsCtmvXrvLCSkzeq6n6UKrBg08sGyF9nW1hmKEAZGAjSg2zcePGwjY1THjtCJ/FnMNzAI6Q0TPBmNR94oiJ2bJlSzkxx48f77O2aE9HsmFcYHj5CBnmoe2OvJVczESAihqm02tn3SD/c41J3QeGu3btEnXq1JFEOH36dB81mXGqim6BtjvCME3RdjcDHbOsoKaGmei1v/3222YBbpE1TOppDtbmzZtFuXLlpDytW/hfmtVGepoKhUMYpkna7pGCYmDjeJiNX1QUvVp47Yjgodq/MKYTk3oaKK9cuVK+Ro90b2vWrEmjBvNOUWGY55xzjnHa7uahFY1FSErerFkzSXgPPfRQNEaE0Cp77f5AZlJPEb8XXnhBHHfccaJSpUpi69atKZ5t5uEqDBPeUbrp68zsGR2rtm/fLmrWrCkJfdasWXQ6lklP2GvPBJxMdjGpZwJO4q7JkyfLi+qSSy4R+/btS9xt5f9K2x2SrCD1Dz74wMp+UDZ6w4YNMvwPapiLFy+m3NUMfUNYrTNChtfaM0CUYQOTegZI3Dfcd999kvTatWvnfoCFW51hmEhfd9JJJ1nYC9omL1u2TCYlL1q0qIizGuYrr7zCa+0epzqTugegBg4cKAn9xhtv9HC0+Ye4hWEiT2qq6evM76ndFs6dO1eqYVatWpXVMIUQ8Np79+4tr0UsRbHX7j6/mdTdcTmytVu3bnISDR069Mg2m78kC8NE+jqEyXExAwGlhtmoUSPBaphHj4nTa0+mJnr0GfH6j0k9yXhDWa5Vq1aS0MeNG5fkKLs2qzDMRG33jz76SPbTS/o6u3psp7XqfQEl12BnL4K1OtFrpxKFpgM1JnUXFHfv3i3q1q0riW7atGkuR9i3CWGY0HZHGGaitjv6iIekNkkE2zcC3ixmNUxvOKmj4LWXLFlSzl/22v9BhUldzY5/P5F0GaJWeGiIkCoKBWGY0HZHGKYbcSO6AITPJVoEOnfuLMmJ1TBTGwfk/3Wutcfda2dSd8yfVatWiTPPPFMULFiQzEMYFYbZoEGDpGGYeJM0s/R1Doj4awAIgJSaN28uCX3ixIkBtBCPKtlr/2ecmdT/ne8vvviiyJEjh6hYsaL49NNPSVwF9957rySKzLTdVfo6iq+c2zCIO3bsELVq1ZLjNHPmTBtMNtpG9to58bScoFOmTJEX1cUXXyy+//57oyetV+O8artDtAvr6VT0a7ziY8JxGzduFGXKlJFqmIsWLTLBJDI2vPzyy7Fda4+9p37//fdLUmvbti2ZCZ1KGOYjjzwi+4+Hw1zCQ2D58uUif/78okiRIqyGGRDs8Np79eol5zd+DcVlrT3WpH777bfLAe/Ro0dA0yrcatMJw4TiX4kSJcI1NOatISl59uzZRZUqVVgNM4S5AK8dcxy/SO+8884QWoy2idiS+vXXXy8HeciQIdGOgKbW0w3DPPfcc4+kr9NkCleTCQJKDRNv8B44cCCTI3mXTgQSvfbEsF6dbUVdV+xI/fDhw6J169aS0JG2jUJxhmGmsjau0tc9+OCDFGAwvg9KDbNDhw7G20rVwDh47bEi9T179kh9E/wMQ8o2CgVhmAUKFJBhmKmuGb7xxhvy5oYXk7gEi4BSw8QaL5doEYAuvXOtnZrXHhtSx6vwWGo48cQTBeJZKRSEYULbHWGY6Wi7K8/x119/pQCHsX3o0qWLvHkOHz7cWBvjaBhVrz0WpL569Wpx1llnCWT1oZKxXIVhQts93TDMNm3ayLdM43hBh9Fn6JO0aNFCEvqECRPCaJLbSBEBil47eVJ/6aWXxPHHHy/OP/988cknn6Q45GYerkvbHcmlb7jhBjM7ablVO3fuFLVr15aEPmPGDMt7Q9988ASVCBnSpP7UU0/Ji6p+/friu+++IzEzVRimX233bdu2SWwg8cpFLwKbNm0SZcuWFYlqmHpb4dp0IwCvvWfPnvK6wA0ZL+bZWMiS+gMPPCAH54orrhB///23jWOTwWadYZhYj8cD4/fffz9DO7whfQRWrFghxdHwK4jaA7j0UbHrTHjtxYsXl9fHqFGj7DJeEJUJGDRokByQ7t27WzcgbgYHEYaJ+HxOX+eGdvrblBpm5cqVXdUw06+ZzwwbAZu9dnKeOtaI4YEi5yaFElQYJl5+gWY8Fz0IKDXMhg0biv379+uplGuJHAEbvXYypA61QURzgNCpvEzjDMPUre1+yimncPo6TZThRQ1TU1NcTQQIHDx40Kq1dhKkvnfvXnHRRRdJQn/66acjGHb9TSIME9ruCMPUnWBXpa+bPXu2fsNjVqNXNcyYwUKyu3gOZcNau/Wk/vHHH4sKFSqIE044QeBlAgoFP/mg7Y4wzCC03adPny5vgOm8sEQBX1196Nq1q8Rx2LBhuqrkegxHwOm116lTx8gIGatJ/c033xRnn322/MN3CkWFYULbPagwzL59+3L6Oh+T5c8//xQtW7aUhD5+/HgfNfGptiLg9NpHjx5tVDesJXV45fDO4aXDW6dQnNruQYZhIn3d5ZdfTgGy0Puwa9cuAQ8Nz27wi4dLfBGA1473RTAXMCfWrl1rBBhWkjrWzQEk1tGxnk6hqDDMoLXdcbOAXgynr0t91mzevFmUK1dO5MyZkzNFpQ4f2TPgtRcrVkxykgleu3WkjsgWEDoiXRDxQqGEGYap0tfpjqahMA6Z9QFKllDDLFSoUGwy6GSGB+87GgGTvHarSB2x5yB0KnolUYRhPvrooxJDLCNw8YYAPDH8uqlUqVJaapjeWuGjKCBggtduDanj7VAQOpYpKBRnGOYzzzwTWpc6d+7M6etSQNuphrlv374UzuRD44oApKyjXGs3ntSxBgz9FhA69FwoFDzYPe+88+SD3rC13aEpz5l3vM0iXWqY3lrjo6ghANmIKNbajSZ1hPRBYRGEjlA/CgWhl9B2Ryhm2NruP/74I6mbY5DzYeDAgRIrv2qYQdrIdZuPgNNrhyxHGBEyxpI6tM/x8g200PEyDoWCMEz0B2GYUWi7q/R1UBLkkhyBbt26SUIfOnRo8oN4DyOQAgJOr33MmDEpnJn6oUaSOjxYvB4Pjxavy1MoKgwTvzyiCsNUGiW//PILBUi19+HQoUOiVatWktDHjRunvX6uMN4IwGtHyDJWHuC1r1u3LhBAjCN1rDEjjyjWfqFRQqE4td2jDMPEswlEcHDJiMDu3bvlhYYLbtq0aRkP4C2MgCYE4LUXLVpUknsQXrtRpI4oEFxU9erVE5CcpVBUGKYJ2u5I3IBEG1yORmDLli3SiYC+PMfvH40N/xcMAkF67caQ+tixYyWht27dWiApBIViUhjm9u3bJb6TJk2iAK22PqxatUqqYRYsWFC7GqY2I7kisggE4bUbQerIwgMPnYoXaWIYJl6KAMacvu4/flBqmBUrVgxEDfO/lvgbI5AcATzjcq61Jz/S257ISV11BgmVKRRnGKZJ2u6I5MCzCi7/IOBUw/z+++8ZFkYgcgTmzZsn19r9GhIpqbdt21Z6j1AnpFAQpohwRYQtmqbt3qhRI05f9+8kc6phUph33Ac6COiITIuE1OEZQS8cywF4DZtCQRgmXihCGKaJ2u5IX9e/f38KUPvqA34RYt4FrYbpy0g+mRHwgUDopI5MPljDRGYfrPNSKAjDhLY7Xv03MQwTsgQgslmzZlGAO+0+4JkNcMAzHC6MAFUEQiV15NpElAFybyLqgEJRYZjQdjc1DDPu6esQTYWoKhA6oqy4MAKUEQiN1BH/izjg8uXLC8QFUyhObXeTwzD79esn8ufPTwHylPuAGy3eewChT506NeXz+QRGwDYEQiF1vKGHiwqvxuLNPQpFhWHaoO1es2bNWKavw1IYlsQQ9RO2GiaFOc59sBOBwEkdGhogdGhqQFuDQrEpDFOlrxsxYgQF6D33QalhQkMobDVMz0bygYxAAAgESuqIjQahQ/WOSrEtDBNSnxiDOHmqSg0TKp9RqGFSmevcDzsRCIzUVeYP6FJTKM4wTJu03eOWvs6phokXwbgwAnFDIBBSb9eunfQOkTmGQkEYJrw+hGHapu3epUsXUbx4cQrDkGUfnGqYWHbiwgjEEQGtpI4cjpdccokk9MmTJ5PAE2GYWJdFGKaN2u54UNi+fXsSY5FZJ5C7FstMJqhhZmYn72MEgkZAG6lv3bpVanUj6zqUxygUhGEqbXcbwzDjkr4OEUggdMgcc2EE4o6AFlJfs2aNKFSokChQoIBYuXIlCUwR0wyiQIyzrWGYS5culX1Yvnw5iTFJ7AQSjrRp00b2Ee8McGEEGAEhfJP6/PnzRc6cOUW5cuXE5s2bSWCqwjDxFqLNYZiU09chJSDe4sWNF2/1cmEEGIF/EPBF6ur18zp16ohdu3aRwJRSGCbCL6GzQ61AywZqmNDbMU0NkxrW3B/7EEib1MePHy+9pJYtW4o//vjDvp67WEwtDLNIkSKk3hHAkCk1TChimqiG6TKteBMjECoCaZN6tmzZRNeuXUM1NsjGOnbsKG9SVMIwkb4OY0Qpfd2mTZukdw4vHd46F0aAEciIQNqknrEq3sIIMAKMACMQNQJM6lGPALfPCDACjIBGBJjUNYLJVTECjAAjEDUCTOpRjwC3zwgwAoyARgSY1DWCyVUxAowAIxA1AkzqUY8At88IMAKMgEYEmNQ1gslVMQKMACMQNQJM6lGPALfPCDACjIBGBJjUNYLJVTECjAAjEDUCTOpRjwC3zwgwAoyARgSY1DWCyVUxAowAIxA1AkzqUY8At88IMAKMgEYEmNQ1gslVMQKMACMQNQJM6lGPALfPCDACjIBGBJjUNYLJVTECjAAjEDUC/wf9v1WeExEXewAAAABJRU5ErkJggg==[/img][br][br]Select [b]all [/b]lines that could be the image of line [math]m[/math] by a dilation.
Dilate line [math]f[/math] with a scale factor of 2. The image is line [math]g[/math]. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAXIAAAEVCAYAAAD91W7rAAAgAElEQVR4Ae2deXgVVZr/88yP3zgzTgvjzDjTMz0Df84zG8zMrxeXbrBRRFGDTm/0FnqxndZWbNdWULDV7nYZcbrHFhRIwF2BsIOKJCBL9rAm7GHfkhC2AEnA9/ecureSm8pNbtW9tZyq+tTz3MdbVafOeevzll8q33rPrTxhgQAEIACBUBPIC3X0BA8BCEAAAoKQcxFAAAIQCDkBhDzkCSR8CEAAAgg51wAEIACBkBNAyEOeQMKHAAQggJBzDUAAAhDIgsDKg8tk9OIvSf7iL0npwWVZ9ODeIQi5eyzpCQIQiAmB17a8KMPn/aM8tOaHcujMvsDPGiEPPAUEAAEIhIXAodb98tCaHxki/uqW/9YmbIRcm1QQCAQgoDOBlQc/kNGLr5T8xV+U0gNLtQoVIdcqHQQDAQjoSMC0Uh5c80M5qIGVYmWEkFuJsA4BCEAgSeBw6355eM2PtbNSrAlCyK1EWIcABCAgIoaVskRPK8WaIITcSoR1CEAg9gSmJatSdLVSrAlCyK1EWIcABGJL4HDrgS4rZfMLoeGAkIcmVQQKAQh4ScC0Um5d/EUp0awqJdN5I+SZCLEfAhCIPIFpWyYbDzQfXPMDOXhmb+jOFyEPXcoIGAIQcIuAYaWsTVSlTA2RlWI9f4TcSoR1CEAgFgRWHfxQbltyldy6+AtScmBJqM8ZIQ91+ggeAhDIhkCnlbI6nFaK9ZwRcisR1iEAgcgSONJ6QB6JgJViTRBCbiXCOgQgEEkCUbJSrAlCyK1EWIcABCJHYFpdoirlgdU/kAMhrErJlBCEPBMh9kMAAqElcKT1oDyy9g6jtHDq5udDex6ZAkfIMxFiPwQgEEoCppVyy6IvyIqQV6VkSgBCnokQ+yEAgdARmF73knEX/sDqsXLgzJ7Qxe80YITcKTHaQwAC2hKIi5ViTQBCbiXCOgQgEEoCnxz6SG5fcrXEwUqxJgghtxJhHQIQCB2BuFkp1gQh5FYirEMAAqEhkGqlTIlwVUqmhCDkmQixHwIQ0JJAl5XyeVlxYLGWMfoVFELuF2nGgUAMCDQ0NEhRUZFMmjRJSktLOz8tLS2unr1ppdy/eqzsPx39qpRM8BDyTITYDwEI2CJQWFgoAwYMkIKCAuOTl5cnAwcONL4rgXdjOXr2kPxi7U+M0sIpm59zo8tI9IGQRyKNnAQEgiWg7riViE+ePLkzkPz8fFEftxaslN5JIuS9s2EPBCBgk0BJSYmoO/DURYm4ujt3Y5lR9z/GXfj9qwtk/2l37u7diEuXPrqT1yUq4oAABEJFQNkqSshNL9y8Q1fbc1mwUuzRQ8jtcaIVBCDQBwEl3IMHD5Zhw4YZDzoHDRqU8924aaXcvOjz8vH+eFel9IHe2IWQZyLEfghAICOB2tpaww9XHrm6C1fruSxYKc7oIeTOeNEaAhBIQ0D54ePGjUuzx9mmVCvlFapSbMNDyG2joiEEINAbgYkTJxoeufLJhwwZImPHjhWnJYerDy2X/1x6jdy86P/Jx/sX9TYU29MQQMjTQGETBCBgn4C6Ex86dKgUFxeLql5Roq78clWOaHfBSrFLKn07hDw9F7ZCAAI2CChPXIm2dTHLETN55UfPHpZH195plBa+sulZazes2ySAkNsERTMIQKAnAXU3rqwU66IEvn///tbN3daxUrrhyGkFIc8JHwdDIN4E1B23Emyz7FD9xooSdrVN3ZX3tsyo+61xF/7zTwpkHxN8esNkeztCbhsVDSEAgXQE1ENNdQeuvHH1UeWH5sQga/tjykpZh5Vi5ZLrOkKeK0GOhwAEbBFItVKWU5Vii5ndRgi5XVK0gwAEsiZQWG9aKd+Xfad3Z90PB6YngJCn58JWCEDABQJYKS5AtNEFQm4DEk0gAAHnBFYf+li+tvTLMmrhf8jy/Qudd8ARtgkg5LZR0RACELBLACvFLil32iHk7nCkFwhAQESOnT0ij677L6O08PebfgMTnwgg5D6BZhgIRJ3AmsNYKUHlGCEPijzjQiBCBLBSgk0mQh4sf0aHQKgJNJ49Io9hpQSeQ4Q88BQQAATCSQArRZ+8IeT65IJIIBAaAoX1vzMeaN73yfdk76ldoYk7qoEi5FHNLOcFAQ8INJ7DSvEAa85dIuQ5I6QDCMSDwJrDK+RrS78iNy38d/lo/4J4nHRIzhIhD0miCBMCQRIowkoJEn/GsRHyjIhoAIH4EkhYKT9lgo/mlwBCrnmCCA8CQRFYe3iFfN20UvZhpQSVBzvjIuR2KNEGAjEjgJUSroQj5OHKF9FCwFMCjeeOymPrElbKy5t+7elYdO4eAYTcPZb0BIFQEzCslGXJqhSslFDlEiEPVboIFgLeECiq/1/jgea4T74re07t9GYQevWMAELuGVo6hoD+BJrOHZXxppWyEStF/4yljxAhT8+FrRCIPIG1h0vk68uGyk0L/00+2jc/8ucb5RNEyKOcXc4NAr0QmImV0guZcG5GyMOZN6KGQFYEDCulLFmVgpWSFUMdD0LIdcwKMUHAAwKmlXLjwn+TD7FSPCAcXJcIeXDsGRkCvhHotFJWUZXiG3SHA21sapWr5mx2eFSiOUKeFTYOgkA4CDSdOybjy+4ySgv/d+OvwhF0DKMsqj8ml0wpl88V1WR19gh5Vtg4CAL6E1h3uES+sWyoYKXonat7VjVI3stlcuuSbXKktT2rYBHyrLBxEAT0JjBz68uJCT6rviN7Tu3QO9iYRrepOWGlKBF/svJAThQQ8pzwcTAE9CLQfO6YTMBK0SspaaIp2tpoWCl/W1Qji/a0pGnhbBNC7owXrSGgLYF1h0vlG8uGyY0LqErRNkkics+qPQkrZfE2OZyllWI9P4TcSoR1CISQgGml3LvqO9KAlaJlBjc1n5Wr5mwxRDxXK8V6ggi5lQjrEAgRAayUcCQrYaVUiFtWivWsEXIrEdYhEBIC646YVsoQ+WDfvJBEHb8w7/3EfSvFShEhtxJhHQIhIDArWZWClaJvsjY3n5WrTSulIreqlExniZBnIsR+CGhEoPlco0wouzs5wecZjSIjlFQCM7c2yh9NqZC/cakqJbXvdN8R8nRU2AYBDQmUHSmVby4bJiMXYKVomJ7OkEwr5RYXq1I6O+/lC0LeCxg2Q0AnArO2/t64C7931bel4eR2nUIjliQBw0qZm6hKmeSxlWKFjpBbibAOAY0INJ/vslJ+txErRaPUdAsl1UpZ2JD7BJ9undtYQchtQKIJBIIggJUSBHXnY6ZaKYdcmuDjNAqE3Ckx2kPABwKpVspurBQfiDsfIkgrxRotQm4lwjoEAiRw/HyjPJ6sSsFKCTARGYaepapSpiaqUoKwUqzhIeRWIqxDICACZUdWyjeXXSsjFwyWD/YWBxQFw2YiMC45wUdVpQRlpVhjRMitRFiHQAAETCvlnlXfFqyUABJgY8gtzWflms6qlP02jvCvCULuH2tGgkAPAsfPN8njZT8zSgt/t/HpHvvZoAcBZaX88dQK+WxhtSxoOK5HUClRIOQpMPgKAT8JGFbKB9fKDQsGyzKsFD/ROxrLtFJuXrxVDp5pc3SsX40Rcr9IMw4EUgi8vvUV4y4cKyUFimZftxzvslImVuhlpVhRIeRWIqxDwEMC3ayUDVgpHqLOqWvdrRTrySHkViKsQ8AjAuVHVsq3sFI8outet2GwUqxni5BbibAOAQ8IdFkpY2T3yW0ejECXuRJQVsqXk1Upulsp1nNFyK1EWIeAiwQMK6U8UZXyW6wUF8m629Xr2xrlT6ZWyF9rWpWS6WwR8kyE2A+BLAmUH1kl3/rgq3LDgn+VZXvnZtkLh3lN4L7kBJ9Ri/StSsnEACHPRIj9EMiCgGml/GzlGNmFlZIFQe8PqUuxUp7QvColEw2EPBOhLPdPnjxZhg0bJg0NDVn2wGFhJNByvlmeKL/HKC387YanwngKsYg51UqZr+EEH6dJQMidErPRvqWlRQYMGCB5eXlSUlJi4wiaRIFAp5UyHytF53zetzrxMmRlpRzQdIKPU34IuVNiNtoXFBTI0KFDpX///lJYWGjjCJqEncAb2xITfLBS9M1kNyulXO8JPk4pIuROiWVor6wU805cifnEiRMzHMHuMBPASglH9qJmpVipI+RWIjmu5+fnG3fjqhsl5OrunCWaBEwrZcT8f5WlVKVom+SfR9BKscJGyK1EclhXfrh5N666GTduXKeo59Ath2pI4I1tU4wHmj9b+S3ZdXKrhhESUv3xs/KV4sTLkJ+ImJVizS5CbiWSw7r1DlzZKoMGDcqhRw7NhoDiPmnSpM5PaWlpNt2kPSbVSvkfqlLSMtJh4xvbGuXSqRXyV4XVMn+3fj876zYjhNwlosXFxcbduLojt35cGoJubBAwn1EMHjzY+GtI/eOq8jFkyBBR1US5LBVHP5ExHwyXEfP/RZbunZNLVxzrIQHTSrkpQlUpmXAh5JkI2dw/cOBAUf64slfMj6olVyJCLblNiC40M/9BTRXt2tpaIw+5PHjGSnEhOR53kWqlPB5xK8WKEiG3EsliXZUYphNs8+6QWvIsoGZ5iBJr9Y+qdVF36NkI+Ym2ZplYfq/hh2OlWKn2vq5Yq7+ClLWo/nH1ejGslFcTVsq8GFgpVp4IuZWIw3Vz8k9vIqEEnlpyh1BzaG59TqG6Mu/InQoKVkp2iVD/L6g5FIq3uonx+i/SVCtl/2k93+CTHUn7RyHk9lmlbWletKl/yqc2VHeHvYl8aju+u0NA/cOpfhrBfNh53333GbNsnebAtFLuXvkt2XmCqhQn2fHrmq9v6apKiZuVYs0HQm4lwnpoCZh33uaDTvVfJexKzO0uJ9qOp1gpv7R7GO2SBPyyE99UVSnKSplRLXG0UqwXHEJuJcJ6aAmYzypST0AJi/oz384duWmlXD//X2TJHqpSUjna+a4e9qt/OM2P4u7Fcv/qvZL3cpmoqpS4WilWrgi5lYgL601NTS70QhdOCfQ2Acv87Zu++ntz21TjgebdK78pO0/U99WUfX0QUP9gqr+EvFi2tpyTocV1hohPiFlVSiaeCHkmQg72b9682ahdVnckl156qYwfP97B0TTNlYASECXm1kU9AFWfdAtWSjoq2W9L97A5+966jnxze5P86auVcsWMaimOYVVKF4n03xDy9Fyy2nrllVd2/llp/nk5a9asrPriIOcEFHNrhZBZy5+uYqXy6Gr59gfXyfXz/1mW7JntfECO6EEgXQ56NHK4wbRSbly4VfbFtColEzKEPBMhm/v37NnTQ8TVRT1mzBibPdAsFwKqzE3xVrXLqmpFfdS68mmVmFsXrBQrkdzXzYfN6r9uLFgp9iki5PZZ9dnyxIkTaYX87rvv7vM4drpDQImH8mfNj7ozV+JuLQtNtVJeWk9Vijv0E72ke9icbf9YKc7IIeTOePXZ+s477+wh5uXl5X0ew07/CBhWyodYKV4R7+1hs9Px7l+TqErBSrFPDiG3z8pWyxdffFFGjhwpY8eOldWrV9s6hkbeEzCtlLtWflN2UJXiCfDeHjbbHUxZKcPMqpSyaL3Bxy6DbNsh5NmS4zhtCUyZMkVGjRplPJ+YveA9mVQ+zigtfGn9k9rGHIXA1DOJdA+V7ZzbW9ub5DOvVspfUpViB1ePNgh5DyRsCDOBCRMm9LC3hkwYSFWKx0k1HzZn87sqDyStlJFUpWSdJYQ8a3QcqCOByy+/vIeQj7jlOh1DjVRMyh9P96uTfZ3kNmWlzEtM8BmPldIXqoz7EPKMiGgQFgJtbW09RFz9ua9KEVm8IaAqVV566SXjh8nSlXn2NmqqlTJ3V/Tf4NMbB7e2I+RukaSfwAlUHl0jn7v6ih5i/vzzzwceW1QDUOWeajan+q/dJdVK2csEH7vY+myHkPeJh51hIfDW9leNB5pj594q145MTAbq16+f3HPPPWE5hcjHiZXiXYoRcu/Y0rMPBE62tcikikRVyuSUqhQ1Qaujo8OHCBjCDgHDSnlNVaVUCVaKHWLO2iDkznjRWiMCVUfXyHc+vF6um/dPsnjP+xpFRiipBB7srEqpl72nzqfu4rtLBBByl0DSjb8ETCvlrtJvyI4Tdf4Ozmi2CGxvOSfXdlal7LN1DI2yI4CQZ8eNowIicLLthDxZcZ/hh09ePymgKBg2E4G3tzfJZa9Vyl9MV1ZKc6bm7M+RAEKeI0AO949A1TGsFP9oZz+SaaXcsLBe9mClZA/SwZEIuQNYNA2OwFvbXzPuwn9a+nXZfmJLcIEwcq8Etp/oslIeK8NK6RWUBzsQcg+g0qV7BE5hpbgH08Oe3t7RZaXMwUrxkHT6rhHy9FzYqgEBrBQNkmAjhE4rZQFWig1cnjRByD3BSqe5Eng71UppwUrJlacXx2OleEE1uz4R8uy4cZRHBE61U5XiEVpXu30HK8VVnrl2hpDnSpDjXSNQdWytfOfDEcZDzUV73nOt3zh3ZH3VnRssHlqbeIPPCKwUN3C60gdC7gpGOsmVAFZKrgS7jle/DW6+fFr9+qP6qJdSZ/Nb4V29iuw4cU6+mpzg8+g6qlJS2QT9HSEPOgMxH/9U+0l5suLnxl34i+vt/4JezLH1evrmC5ALCgqMl08r8VbC7uTXCdN1rqyU/q9Vyp9Pr5LZVKWkQxToNoQ8UPzxHrz62Fr5rmmlNGCl5Ho1qNesqbtvJeZuLqlWSgMTfNxE61pfCLlrKOnICYG3t0/rmuBDVYoTdL22VW/oyc/P73W/0x1YKU6JBdceIQ+OfSxHPt1+Un6JleJ67s278draWlf67mal7OS3UlyB6mEnCLmHcOm6OwHDSvkoWZWCldIdTo5ryhN3+s7M3obESumNjL7bEXJ9cxOpyEwr5b9KvybbWjZH6tx0OBn1ujX1yWVRVsrw+YmXIVOVkgtJ/49FyP1nHqsRu1kptVSleJX8XIX83R1NMuC1SrlcVaVgpXiVJs/6Rcg9Q0vH1cfWyXc/usF4qLmw4V2AeEggFyF/ODnB5/oF9UJViodJ8rBrhNxDuHHu+p1kVQpWij9XweTJk43SQ1UzbnfZmWKl/IIJPnaxadkOIdcyLeEN6nT7Kfll5f2JCT61T4jIp+E9mRBFrqbiq4edAwYMkKKiIiktLTU+kyZNSjuj07BSplXK5dOq5H2slBBlOn2oCHl6LmzNgkDNsXXyPayULMi5c4gSc7N6xZyarywX69T8VCtl90lehuwO/WB7QciD5R+Z0TutlBKqUnRN6s6TqiqlXvJeLhOsFF2zlF1cCHl23DgqSSDVSvnv2ifkU6wULa+Nd3c0y4BpVVgpWmYn96AQ8twZxrYHrBR9U3/q1KnO4B5Zu8+4C1dVKVgpnVgi9QUhj1Q6/TuZd3ZMNx5o3lnyn7K1ZZN/AzNSnwTGjx8vl112mVHB8pXh18vVUz/ESumTWDR2IuTRyKNvZ3Gm/ZQ8laxKwUrxDbutgaZPn24IuPmgU/233z98Xt6jKsUWvzA3QsjDnD2fY685Vibf+2hkcoLPOz6PznCZCNx+++09hFyJ+ZEjRzIdyv6QE0DIQ55Av8J/FyvFL9RZj/P17xWkFfLW1tas++TAcBBAyMORp8CiPNN+Wp6qfMC4CzeslE+Z4BNYMvoYWNknn3no1R5Cftddd/VxFLuiQgAhj0omPTiPmsYuK2VBA1aKB4hd6fKRdYmqlOvm18us+UtkzJgxMnz4cHnhhRdc6Z9O9CeAkOufo0AixEoJBLujQXedPC9KvNUEH1ViyBJfAgh5fHOf9sxTrZQXah+Xi59eTNuOjcESUL+P8mfTqoxJPlSlBJsLHUZHyHXIgiYx1DaWyfeTVSlYKZokJU0Yanq9ugtX0+3VXTkLBBByrgGDwLs7ZiQn+NwuW49vhIqGBNSsTDU7U4n4w1gpGmYouJAQ8uDYazFya8dpeTpZlYKVokVK0gahrBT1k7MDplWK+t0UFgikEkDIU2nE7HttY7l8/6MbjTvxBQ1vx+zsw3O6XVZKnezESglP4nyMFCH3EbZOQ5lWyk9Kbpd6rBSdUtMZS3crZW/ndr5AwEoAIbcSifg6Vko4EmxYKdNNK6UpHEETZWAEEPLA0Ps/cKqVMn83Vor/GbA3Yjcr5cQ5ewfRKtYEEPKYpP+9ZFUKVoq+CVdvsB/RWZWClaJvpvSLDCHXLyeuRtTacUaernzQeKD5Qu0EufjpBVf7pzN3CMze2Sx/Pr1K+r+mqlKwUtyhGp9eEPII53p9Y7kULE9UpWCl6JvoR5MTfL46v052YqXomyiNI0PINU5OLqG9t6PQuAv/ScltUn98Qy5dcaxHBFKtlIfWYqV4hDkW3SLkEUtzqpXyfM0EuYCVomWGZ+/qslLewUrRMkdhCgohD1O2MsS6vrFCCpbfZNyJY6VkgBXg7k4rZV6d7MBKCTAT0RkaIY9ILlOtlDqsFC2zipWiZVoiERRCHvI0nu04I89UJapSsFL0TeYcrBR9kxOByBDyECexu5XyVojPJNqhP1aW+NnZr2KlRDvRAZ4dQh4g/FyGNq2UO1bcJlgpuZD07tg9p87LDckJPg+uoSrFO9L0jJCH7Bo429Eqz1Q9ZDzQfL5mvFz4tCNkZxCPcJWV8hfTq+Sy1yrlbapS4pH0AM8SIQ8QvtOhU62UebuxUpzy86u9aaVcO69OtlOV4hf2WI+DkIck/e/vLDLuwu9YMVrqjq8PSdTxCtOwUhYm3uCDlRKv3Ad9tgh50BnIML7VSunASslALJjd3ayU7fxWSjBZiO+oCLnGud/QVCFjkxN8sFL0TRRWir65iUtkCLmmmcZK0TQxKWFhpaTA4GugBBDyQPH3HDzVSnmuZrx0XKQqpSel4LfMTValfEZVpWClBJ+QmEeAkGt0AWxoqpSxy0cZDzXn7X5To8gIJZXA+OQEn2GqKqWFN/iksuF7MAQQ8mC49xjVtFJ+vGK0bKEqpQcfHTbsPXVeRiarUh5ggo8OKSGGJAGEPOBL4dyFs/KrqoeNu/Dnah6TjovtAUfE8OkIzN11XP5yRpV85tVKeQsrJR0itgVIACEPED5WSoDwHQw9vmy/5L1cJspK2YaV4oAcTf0igJD7RdoyzuydM427cMNKaWaCjwWPFqt7T7fJyIVbDRHHStEiJQTRCwGEvBcwXm3GSvGKrLv9JqyUaqwUd7HSm0cEEHKPwKbrNtVKKd5FVUo6Rjps67RSirFSdMgHMWQmgJBnZuRKiy4rJV+2NNe60ieduEtg3+k2uRErxV2o9OYLAYTcY8ypVsqzNY9JO1UpHhPPrvvi3cflihnV8qdUpWQHkKMCJYCQe4h/Y1OV/GD5zcZDzeJdb3g4El3nQmBCsiplaHGdbKUqJReUHBsQAYTcI/BYKR6BdbHbVCvl/tW8wcdFtHTlMwGE3GXg5y+ck19XPWLchT9b/ai0X2xzeQS6c4NAqpXyJhN83EBKHwESQMhdhG9YKR9jpbiI1JOuJpQnJvhgpXiCl04DIICQuwTdtFJ+tCJfNlOV4hJVd7vBSnGXJ73pQwAhzzEXhpVSjZWSI0bPD5/XWZVSIW9u4w0+ngNnAF8JIOQ54E61UuZSlZIDSW8PfTxppXyleAtVKd6ipveACCDkWYKfs3OW8UDzRx/fKpuba7LshcO8JLD/dJvctCjxWyk/X73Hy6HoGwKBEkDIHeLHSnEILKDmykr5qxnVcumrFfLGtsaAomBYCPhDACF3wHlTU7X88ONbjDvxubted3AkTf0kkGql1Lec9XNoxoJAIAQQcpvY5+zCSrGJKrBmWCmBoWfggAkg5BkScP7Cefl19S+Mu/DfVD8qbUzwyUAsmN2GlVJYLZdOxUoJJgOMGiQBhLwP+lgpfcDRaFc3K+U4VopGqSEUnwgg5L2ANq2UH358q2yiKqUXSsFu3n+GqpRgM8DouhBAyC2ZaLtwXn7TaaX8QtQ6i34E5quqlMJq+ROsFP2SQ0S+E0DIU5BvaqYqJQWHtl+fSE7w+XLxFqnHStE2TwTmHwGEPMlalRMOn/ePRnmhEnQW/QgcONMmo5ITfO5jgo9+CSKiwAjEXsixUgK79hwNPL/huPx10kp5nQk+jtjROPoEYi3k6iGmepip7sTVw00WPQl0Wilzt0gdVoqeSSKqQAnEVsi7WSlNWCmBXoW9DI6V0gsYNkPAQiB2Qt52sasqRU30URN+WPQjgJWiX06ISF8CsRJy9SuF6tcKsVL0vSBVZE9UJN7g82WsFL0TRXTaEIiNkGOlaHPN9RrIwTNtcrNZlfIJPzvbKyh2QMBCIPJCrn4bRb0EWd2F/7r6EVE/Q8uiH4EFDcfls4XV8sdTK2QWVSn6JYiItCYQaSHvZqXspCpF1ytxYtJKuWbuFtlCVYquaSIujQlEVsjVq9fUXfgPPr5Z1CvZWPQjYFgpixNv8BmHlaJfgogoNAQiJ+TtWCmhuPi6WSlbeYNPKJJGkNoSiJSQb26ulR+tSFalYKVoe9FhpWibGgILKYHICHkxVor2lyBWivYpIsCQEgi9kHezUqqoStH1OlzY0CKfLUpWpWCl6Jom4gopgVALecJKyTceas7eOTOkKYh+2JMqDkjey2VytapKaeYNPtHPOGfoN4HQCjlWit+XivPxDp1pl1sWbzNE/F6qUpwD5AgI2CQQOiFvv9guz9Y8ZtyF/6rqYTl3gTs8m7n2tZmyUv6mqEb+aEqFzMRK8ZU9g8WPQKiEfEtzrfx4BVaK7pdpqpWyGStF93QRXwQIhEbIi3e9mZjgs3yUbGyqjAD66J3CoVaslOhllTMKAwHthbzjYrs8h5Wi/bW0cA9WivZJIsDIEtBayLFSwnHddVopc7YIVko4ckaU0SKgrZAX705YKWOXj5INWClaXnVYKVqmhaBiSEA7IcdKCcdVuChppVxCVUo4EkaUkSaglZBvaV4vP14x2nio+f7OokiDD/PJPZmc4HMVVkrWaSwpKZFhww1C7QwAAAVtSURBVIZ1fkaPHi1FRVzzWQON+YHaCPk8rBTtL8XDre1ya3KCzz2reINPLgmbOHGiDBw4UNR/1aegoEDy8vJkyJAh0tLSkkvXHBtDAoELecfFDnmuZnxygs9Dcq6jNYZp0P+UlZXyt0U1oqyUIib45JywoUOHSn5+frd+amtrDTEfN25ct+2sQCATgUCFvO74erkDKyVTjgLf/2Rl4rdSrpqzWTYxwceVfPTv39+4E7d2pu7MBw0aZN3MOgT6JBCYkGOl9JkXLXZ2t1IatIgpCkGYd97KJ7cuymZRFgsLBJwQ8P2KSbVSnql6SM5ipTjJl29tu6yUcimqP+bbuHEYqLCwsFexRsjjcAW4f46+CjlWivsJ9KLH7lYKzyzcZqw88MGDB6ftVu1TtgsLBJwQ8E3I5+1+y3igWbD8JlnfWOEkRtr6ROCIqkpZkvjZ2Z+twkrxCrt60Km88HSLqmSxPgRN145tEEgl4LmQX/i0Q55PVqVgpaSi1+v74j0t8rmiGvnDKeVSiJXiaXKUB67sFetSXFxsWC7qvywQcELAUyGvO75B7lhxW3KCT88L10mgtPWOwC+TVSlXztksG5uwUrwjLaIecCohVw88Uxe1PmDAAO7GU6Hw3TYBz4R8PlaK7SQE1VBZKflYKb7inzx5cueDzoaGBiktLZWxY8d2ijiTgXxNR2QGc13IL3x6QZ6vmWDchT9T9aCc7TgTGVhROhHDSplZI3/4ClaKn3k1Z3Cqu3LzozzxdFaLn3ExVrgJuCrkqVbKezuwUnS9NLBSdM0McUEgOwKuCTlWSnYJ8POoI2exUvzkzVgQ8ItAzkKeaqU8XfWgtGKl+JU7R+MsUVUpM2vk/2KlOOJGYwiEgUBOQl5/fIP8pCRRlYKVom+6n0pWpXxpNlUpOmXp4Ycflssvv1z69etn1JW3tbXpFB6xhIhA1kI+f/fbyQk+N8r6xvIQnXJ8Qj16tl1GJ6tS7maCj1aJf/bZZzsfdpoPPVX1CgsEsiGQtZAPn/dP8nQlVko20P04ZsneFvm7pJUygwk+fiB3NMaVV17ZQ8gvueQSR33QGAImgayFHCvFRKjff1OtlA1M8NEvQSJy3XXX9RDyK664QstYCUp/AlkLuf6nFr8Iu1kpK/mtFJ2vgFmzZvUQ8vHjx+scMrFpTAAh1zg5TkLDSnFCS4+2r7/+uowYMUKuueYaefHFF/UIiihCSQAhD2Xaugf9VFXiDT6qKgUrpTsb1iAQBwIIeYizfCy1KgUrJcSZJHQI5EYAIc+NX2BHL01WpfR7pVxm1PEGn8ASwcAQ0IAAQq5BEpyG8HTSSvni7M2ynqoUp/hoD4HIEUDIQ5RSZaXctjTxBp+7sFJClDlChYC3BBByb/m61ruyUv5+Zo0oK2U6VoprXOkIAlEggJCHIItYKSFIEiFCIEACCHmA8DMNfexsB1ZKJkjshwAEBCHX9CJYuveE/P2sWun3e6wUTVNEWBDQhgBCrk0qugJ5uuqg5L1cJkZVSiMvQ+4iwzcIQCAdAYQ8HZWAtjWeU1bKdkPEf0pVSkBZYFgIhI8AQq5JzpbtPSEDZ9XK//l9uUyjKkWTrBAGBMJBACHXIE/PJK2UL7y/WWqxUjTICCFAIFwEEPIA86WslNuxUgLMAENDIBoEEPKA8rhsH1ZKQOgZFgKRI4CQB5BSrJQAoDMkBCJMACH3MblYKT7CZigIxIgAQu5Tsj9IWil/QFWKT8QZBgLxIYCQxyfXnCkEIBBRAgh5RBPLaUEAAvEhgJDHJ9ecKQQgEFECCHlEE8tpQQAC8SGAkMcn15wpBCAQUQIIeUQTy2lBAALxIYCQxyfXnCkEIBBRAv8f9dZOwlBBxvsAAAAASUVORK5CYII=[/img][br][br]Which labeled point could be the center of this dilation?
Quadrilateral [math]A'B'C'E'[/math] is the image of quadrilateral [math]ABCE[/math] after a dilation centered at [math]F[/math]. What is the scale factor of this dilation?[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAO0AAADNCAYAAABU4fe5AAAgAElEQVR4Ae2dCZwVxZ3HQV03iQeua5JNTKKbLMt6RaPxiDGRXRGNbAIeEEM0eLAYjUZCjEQjSMISTYgr8UAZbhQQuUFAGGRGGHCGYWaYYe77Zu4ZZobhGIbffn4N1XS/effr9173e//6fN7ndffrrq76VX1fVf/rX9UDIEEUEAUcpcAAR6VWEisKiAIQaKUSiAIOU0CgdViBSXJFAYFW6oAo4DAFBFqHFZgkVxQQaKUOiAIOU0CgdViBSXJFAYFW6oAo4DAFBFqHFZgk17kKtLe3Izk5Wf8EmxOBNljl5DpRwE8FCOvEiRNx0UUXYcCAAfqH+/wt0CDQBqqYnC8KBKAAobzuuuswaNAgLFy4UL+Sx9euXavvB7Ih0AailpwrCgSowLhx4zRgs7KyArzS8+kCrWdt5BdRICQFCCq7w8YWNqQIT18s0FqhosQhCrhR4Nlnn9VaWTc/hXRIoA1JPrlYFPCswLXXXgt2j60OAq3Vikp8osBpBdg1fvnlly3XQ6C1XFKJUBQ4pYBAKzVBFHCYApdddhn4XGt1kJbWakUlPlHgtAJ8nqUDRUVFhaWaCLSWyimRiQJnFKADBZ0qCO60adM090V+jxo16sxJQWwJtEGIJpeIAv4qQHDZ4t5+++3amC2/Q+0yC7T+qi/niQI2UUCgtUlBSDJEAX8VEGj9Vcrh59Gljs9T6uPw7Ngi+ceOHYtKOgTaqMge2ZvymYpjhup5KhxeOpHNUXTv1tHRgdGjR2uaXnDBBXj++ecjmiCBNqJyR/5myv/Vylkmkc+Fve744IMPasDyj1B9Zs2aFbFECrQRkzryN+L4ICtVUlJS5G8eo3csbjuMgQMH6rAqaO+4446I5VigjZjUkb/R66+/HpZZJpHPSeTv2Hq0F9trOvDXzHo8uK0EQ5bux4C3U7XPWedd2A/akSNHRiyRAm3EpI78jdg15nMsV0gYOnSoNsjP72BXTIh8DsJ/xxMnTyKzuRvz8pvw1KcV+N7qXPzju3s1OPl9/YcH8FBiKV7JqMP6ijaUdBzB5MmT+0G7atWq8Cf29B0E2ohJHfkbEVh64yhw2U1m68suXTyCW9l5FGvK2jAlrQYjPirEVxZm6K3nN9/Lwn9vKsTkPdVYXNiM9MZu9PT2eSy0mTNnYtAV12Pwrf+JFStWeDwvHD8ItOFQ1SZxElY6rdMrxxiUh47xWCxttx3tRXJdJ17ffxAPby/FVcuzdTgvmrcPt63JwxPJ5fh79kEk1nSgvvt4UNkfujYf0/bWBHVtKBcJtKGoZ/NrVffYNZmqtXU97rR9dm1zWg5rLeOzuyrxw7V5OD8hXQf06uU5+OnWEvwxvRYrS1uR39ZjaRYFWkvllMioAOHkSoCugROzuaqCkwK7thsr2/Gn9FqM2lyEbyzJ0uH86qJM3LWhAL9JqcTc/EbsOdiFjmMnwp49gTbsEsffDdQsE9eFxdhltquDBbu2KQc78VZOAx7bUYbrVuTocJ77ThpuXpWLRz8pw8ysemyubAdhjlYQaKOlfIzfl8DS8PTII49oLoyXX3652+fcSMugurbLilvw3O4q3LE+H/80b58O6Lfe3497txThD6k14Dn7mw/jeN/JSCfT6/0EWq/yyI+hKECrMZ9v2bqyy+xqmAolbn+uZWu4papdGzYZ/XExCKQa8xw0Nx1D1+XjVzsrMPtAA5LrDqGpp9efaKN+jkAb9SKQBISqgOrazslt1KyzN67MxTnvpOmA0jD088RS/DmjDuvK21DccSTUW0b1eoE2qvLLzQNRQHVtV5S04IXPqnH3xgJ8acGZMc9/WZiBez4qxPN7qrCooAl7G7tx2MuYZyD3ttO5Aq2dSkPSoiugurZ/y6rH2G0l+I9lZ8Y8/+GdNNy0MhcTksoxK/sgtlV3oK47OtPV9ARHcEOgDUJsPqfRLU99uPbOunXrgohJLlFd27l5jXh6ZwVuXZ2Hz8855c7H5096DN2/pRjT9tbiw9JW5LVaO+bpxBIQaIMoNS6aRUdtjjvyQ0MLLaU0tkhwr4Cxazs1rQY/3lSESxdl6s+dF85Nx+1r8zExpRIJeY3YfbAT7UfDP+bpPrX2PirQBlg+6uVGrtPO6DRA9z0J0MYwabV9bX89xm0vxTUfnBnzZOtJ9z46w3Mmy6bKdlREcczTieUl0AZYamr80fUytrzxBq2xa0uvILaUbDHVsMqXF2bg7o2FmtFoaVEzspoP45jNxjxdy9EJ+wJtgKXE51lXVzy2upzV4uoBFGDUtj3d2LWlo/p9W4pxucGd7+zZafjuygOaYejtAw1Iqj2Exp7gnOFtK4KNEibQBlgYbE0JqDJC0ceWEMfKlDNltWXXdvyOcm1ep2o5+f2v72Vp0E5Pr8Xa8jYUtTt7zDPA4rfF6QJtgMVAgxMNT8oIRYjpoue0tZCMXdtJKVUYtr4A/zz/jDvfBQnp2uwVzmJZWNCEtMYudB33PM8zQBnj8nT20qzwChNoA6g+ygjlCiifZwmuHYNr13bM1hIMNrjzsfW8clm25jHEMdGt1R2oiaMxTyvLjGtjTZw4Ue+FcShw0aJF2i3YE+Oog0BrpeJ+xOVpPihbXbbA0Q6mrm1SuTYzhY4IqntL76G7Nhbg959Vg15FB1p7cNJevvDRljDo+ysDJXteqhfGHhlbVwZ+c9+KIC1tACpSdHcWYh7ntLNIBdeuLS20dOFTcJ41OxU3fHgA45PKQcPQrvpO8BoJ4VFA/Wl7M0Syflj1FjuBNoBypMGJBaQCu8lcOZ+trLcCU+cH+u2ua8uurIKT35ctydImZ3OVhI0V7Sg/FL15noHmLxbOJ4g0TBrrhWu+eI67P3vX8/zdF2j9VQrQ4CSgxg//Qa2wHLt2bb+/Og9fMLjznZewFz9Yk4dfnzYMcSW/oyekbxtA8YXlVHZ7fT2r8rHKijqiMiDQKiV8fNOAwPFY9Qm2q+Oua/v1xWfc+dh6XrEsW3OS5yoJ22sOoeGwjHn6KJ6o/ezPahzB1hVPmRJoPSkT4nF3XVtXd74vLtiH4RsKtOUzPyhpQaGMeYaoeuQvZ68r0j7nAq0F5eyua8uVEdSz58C3UzUnhcd3lOGtAw3YfbALncfjzxmevRUOgag36EXyPTQWFHO/KNQQoKsfer8TLT4g0J4WlFPr7rzzTgwZMkQba+vt7W9tdde1pSFIwcnvbyzJxMjNRdpUMq4MX90VP/M8vdVNPtPRYENjHp8D1bMgPcqsGLv0du9w/cZub7iMkN7SLNAC2L17t8m4xIIY9uOR2lgmfW3pkMCuLYdSFKA0En1/TZ42B3R+fpPmDC++8J6rmrIJGM/gMT4TerO8Gs+34zaNUFaNv/qbP4EW0FpWo0VY3/7zRxqkQ5Zm42fbSrSpZFwZvuVI/1bYX8HlPLMCHAqJ5EukzHcPfc/TGK3VxidjSgVaAE8++WS/lpbgfpJdaNRKti1WgC0tu8yRNuRYmQ3mgV191hc1kYTbVo7LuqZXoAWwadOmftByFo8E6xWg0SY5ORk0QtFfO9JdS+tzdCpGGqX43M6Wl3kkzOEKAu1pZd98801c/LXLMODsc3DvvfeiqqoqXJrHdbz6o8eAAdqrQ5RDfVyLEmDmBVqDYDQ60dAU74GthOtMpnBowpaJhhx2LyX4r4BAa9AqXqBVXVR2U/lxBZQQhfOZzCC51p1k62vHkJiYiClTpiAhIQEnTthnXF2gNdSWeICWwCpDCcFU3VXO/VSBY6nhmACh4jd+e5ruaDwnGttTp07VtaFGHE/u6bHH8q0CraFGxAO07iBRc0HZXeVQBbusVgdPQyD8g7DbkE9HR4cJWPXH9tprr1ktS1DxCbQG2eIBWk9zglkxafkkwOFwdmCrTmuxeosev7lv5TxTQ1EGvFl+qAif1HyEeXmv49EF97uFdvz48QHHG44LBFqDqvEArXIjNGRbG6IgtHy2ZavnqVU0XhPoNo1b6g+BfxzqDyLQeEI9v7GnHqkNyVhePA8z9v0OE5Luwx3rrjR9Hkkcgc9f+Ll+4M6fPz/U21tyvUBrkDHWoSU4hJMO+8oIxW3jJG4nOzoYihI9vYeR25qFDRUf4O/Z0zFx18MYuelmE5yjP74dk/eMx7u5f8W26nUo6cjH8b5TvuL8gxk4cKAO7pgxY4zRR3VboDXIH+vQKiOUekbjN4FlBXVq6Dt5AhWdJdhRuwnz82fhpdSnMHbbMBOcIzbegKc/fRCvZU3FmrL3kNWchs7jh3xmub6hDt9+4et4dc00n+dG8gSB1qB2rEPLLqmrkUkZpgi03UPzkQbsbdyFD4rn4ZWMyZiQdC/u2nCtDuid66/BI9tH4I97J2JJ4Wyk1G9HXXc1TiK4FT56+45rca8qXWwraQRaQ3HEOrR8XnVnqaWRyN1xgzQR3Txyogd5rVn4qOJDvJn9v/hNyjiM2vw9HU4+gz6w5Qd4fvd4vHPgL/i4ai2K2nP1rq1ViRVozUracjQ91qH1NA2Ox6PhlcSubVVnGZJrt2BB/t8xJfVX+Pm24Ri27iod0Hs2Xo+nksdgZuZLWF22BJnNqeg81mGuTWHaE2jNwgq0Zj3CvkeLMJ9hXbvBfJ7lcY7RhjO0HmlCemMKVpQswKsZL2hW27s3XKfDOWz91fhF4o8wbe+zWFz4NnbVJ6K2uzLorq0VeRFozSoKtGY9wr5HKAknPXuM7yHiMSvHZY+eOIL8tmxsqlyJN3NmYFLKONy7+VYdTnZt799yG57b/RhmH3gVW6rWaF3bY332W/pVoDVXS4HWrEfY99jCEk7jh61ssGOyJ0/2obqrHMl1H2NhwRuYmvYMHkrs37V9Mnk0Zmb+ATTmZDTtQdvRlrDn1aobCLRmJQVasx623ms92ox9TbuxsnQR/pLxAn6Z9AB+tOE7eut5qmt7N15O+zUWFbyJnXXbUNNVAYLt5CDQmktPoDXrYYs9dm0L2nKwuXIV3s55Bc+lPIr7Nn9fh5NdW+7/NuUR7Xeex/N5XSwGgdZcqgKtWY+Q96qrq7UpZEuXLsWxY95XgGQLyJaQLeLigre0FvIXiXeDLaZy6WNLyhaVLeuHJQu1lpYtbjwFgdZc2gKtWY+Q9jZs2ICzzz5bd7n75je/idLSUi3O9qOt2rMknyn5bMlnTA6jKDg5vMJnUT6T8tmUz6h8VnV61zYkQU9fLNCaVRRozXqEtHfjjTfqwNIazM+1I4dg1KZbdDgJ6U823axZc+mwQMcFOjDEatc2JEENF1M38Yg6JYhAa6gYoWxyRQUFqvH7kn+/CK9m/F4bF6XrH10AJQSugEB7RjOB9owWIW+5a2mfeOKJkOOVCKD1VKSlPVUTBFoLieASsOeee67e4g4ePBjl5eUW3iE+o5JnWnO5C7RmPULeq6+vx22/uxZjXxllq0XIQs5YFCMQaM3iC7RmPSzZe/ST/9aGaCyJTCKBQGuuBAKtWQ9L9uIBWrphGg1uattK/2lVGAKtUuLUt0Br1sOSvXiAlvN+Of+XvtTGTzhewyHQmqulQGvWw5K9eIDW05xgSwR0iUSgNQsi0Jr1sGQv1qH1NCfYEvHcRCLQmkURaM16WLIX69CqOcHh6Aq7KwCB1qyKQGvWw5K9WIeWxiauHqmWf1XflojnJhKB1iyKQGvWw5K9WIfW+O4hZTV2XV3SEiFPRyLQmtUUaM16WLIX69AS0Egupi7QmqulQGvWw5K9WIaWryxh6+q6MJ0lwnmIRKA1CyPQmvWwZC+WoVWrRloilJ+RCLRmoQRasx6W7MUytFyXmS8Pi2QQaM1qRwxaju35u+Kg0xcrj2VoaYTi2/YiGQKF1t96FmoeYvK1IBzH4/tPOTygrIzc5hvivIVwQcv08E3rTIu/QaXb+M2K6y3EMrTe8h2u3/yBls/aXEfaWE6se77GktU7lIzXcdsfH2pf0PLervFy31f98aWj/7XXV0xufucgPBNoXDVfiWQ85nppOKBloXKBcHbtKJw/wWh0MfrX8ri3INB6Uyfw3/yBluVK0FQryzKiq6WvXgGv4bXG8uW2isdban1By3hY11zj9lV/vN2Tv/lXe33FEuDvFMnbO2vCAa16T44S0p8kB3KuMT6nQ+trFUljXiOx7Q+07tKhnEDc/aaO8ZxgWz5/oVX3suo7KtD6cjYPB7TqnzMQEAM511ggToV2+/btuOWWW7TW4Tvf+Q7WrVtnzFbUtoOFVvXqvCWcs5W8NSDervUFLXuT4XA6iSi06hmXGVEQuRMlHNCq+wQCIgudXWrlpsdvX89IvI8Toe3q6sLFF19segY766yzwHWcox2ChZZdY1+vDmUry2dfYxn7m19f0LIVD6b++Lp/RKClMJdffrlWIZgJb8AywXaBVo1JsjvPPPD5hIY0wuwtOBHa1atXm4BlXvlJSEjwltWI/BYMtOrP2dfzI8FmI8LyZTkzz6yrvq5jxn1Bq+oP4zbWHx4PJUQEWgrIroJ6fvAlil2gdSes6nIxT56CE6HlonQKVOP3kiVLPGUzYscDhZbA8c81GDjYkyJgrKO+gi9o3V1PBqivt/rj7jrjsYhAa7wht9llYYvrKdgZWqaZ/8gU31NwIrTMy5VXXmkC99JLL0V3d7enbEbseCDQKmB9WY29JZ5x+ANWMNDyvr5sOt7Sxt+iAq36t/GUOLtDy39ib8YLp0JbVlamPd8NGTIEY8eORXZ2tqciiuhxf6G1AlhmTI2v+moNg4WW9cfbn74vcaMCrS9XODtDywL19VzrVGh9VZZo/e4PtP4C29Li+7286lnUl9ExGGjVH0IwXXelf1ih5b/JokWLNMscb8h/LnpDsevhLdHRgpbdwRtuuEFpo/0bqvTTeMYhEHbr2T32FgRab+oE/psvaNUfqaulVlmEleFzx44dWt2bPn26ngh2o3kezyH4LG/+KfvTEvqCVtV/xhtI/dET52EjrNDSaKMscsq4wedZb95QTGe0oL3kkktwxRVX6FIx/Xz+UGlXDhq+/oEFWl1CSzZ8QcvGQJWRu28F4NatW7XzpkyZoqeL0BqvYX311qDoF/phPQ62/hjv4W47rNC6u6E/x8IJrbf7d3R0+HynrLfr1W8CrVLCmm9f0AZyF/Xq0UCu8XSur5bW03WhHhdoQ1XQzfUCrRtRQjhkJbQhJKPfpQKtQZJotbSGJIS0KdCGJF+/iwVasyTS0pr1sGRPoLVERj0SgVaXQtsQaM16WLIn0Foiox6JQKtLoW0ItGY9LNkTaC2RUY9EoNWl0DYEWrMeluwJtJbIqEci0OpSaBsCrVkPS/YEWktk1CMRaHUptA2B1qyHJXsCrSUy6pEItLoU2oZAa9bDkj2B1hIZ9UgEWl0KbUOgNethyZ5Aa4mMeiQCrS6FtiHQmvWwZE+gtURGPRKBVpdC2xBozXpYsifQWiKjHolAq0uhbQi0Zj1C3uOMk6vHfAvDJtyGgoKCkOOTCACB1lwLBFqzHiHtzZ071zTN65xzzsGePXtCilMuFmhd64BA66pICPtcpsU4N5PbXLZFQugK3LHuSqwqXRx6RBbGILN8DGI6cZZPb28vBg4c2A/aCwd/HmO3DcOLnz2JhQVvILl2C6q7yg25lU1/FBBoz6gkLe0ZLULeuvPOO/tBO2L8cPxx70SM234Phq2/Gqx8/Nyz8Xo8mTwaMzNfwuqyJchqTkPX8c6Q0xCLEcgzrblUBVqzHiHtZWZmwthFJsQ9PT16nMf6jqKgLQebKlfizZwZ+E3KOIza/D0dZMI85uOh+P2eCUjIew3bazai/FARTpw8occRjxsCrbnUBVqzHpbs7d69GwTY39DU04DUhk+xvHguZux7Do9/8hMMX3+NDvNdG67F/+wYhVcyJmNFyXykN6ag9UiTv9E7/jyB1lyEAq1ZD9vs9fb1orSjANuq1+Hd3L/i+d3j8cCWH+ggs1W+b/P38VzKo5h94FVsqVqDovZcHO87Zps8WJUQgdaspEBr1sP2e53HOpDRtAcrSxfhLxkv4Imk+3H3hut0mO9cf432ArDp6b/F0qI5+OxgMhp76m2fL28JFGjN6gi0Zj382uMSqnzTml1C38kTqOwsxY7aTZiX97pmqX5w63/pILNV/smmmzFx18N4I3s6Pqr4EPlt+3H0xBG7ZMFrOgRaszwCrVmPfnvu3l/KdXG5BrLdw+HeLmS3pGNt+VK8ljUVT3/6IEZsvEGHedi6q/Bw4l14Oe3XWFzwFnbVJ6K2uwoncdJWWRNozcUh0Jr1MO2pN+Tx3SvGQJDVAtjG407YJpC13ZXYWbcNiwrexNS0Z/BQ4nAQYLbI/BBsAk7QCTzB5x9AtIJAa1ZeoDXroe+pV01wBXq+JsIY2Mr6esuA8XwnbLOrnNeahY0VK/D37Ol4dtdDWpdagcxvdrnpJMIuOLvi7JKzax7uINCaFRZozXroe2xJCad65YT6ga80CeU1iioep3w3HK7DnoNJeL/oXfwpfRIe2T4CNHYpmGkEozGMRjEaxzKbPgONZVYGgdaspkBr1kPbU60sn1358iT6EPObgW/8Uy90cnNpXBzisBKHlzjMxOEmDjtx+EmBzO/RW36IyXvGY07uTGyrXo/SjkJwGCuYINCaVRNozXpoe2xJjW/GI7RscRkUvG4ui/tDdPig4wcdQOgIQoeQuzZ8W4eZDiOP7xiJGft+h+XF85DWsBPNRxp86pa8MwnfeuhLeOZvE3yeG8kTZMKAQe1oThhgK2qElMniPo1SEgJXgC6YdMWkSyZdM+miOfrj23WQ2SrTlXNSyji8lfNnbK5chcL2A6DLJwNfS0n91eemm24CJ2fYIQi0hlKIJrS0DLOCDB06VP/4+75SQxZk04cCnByR2ZyqPQf/NfNFPJU8xgQyYf7Zhv4TMOz0ByrQGgo5WtAqoxOfW2mIUh8apAizhPArUNVZhqTazViQ/wYeXXC/3sKqlpbfjz/+ePgT4scdBFqDSNGCluOxrmOyTBYhdnfckGTZDIMC7AZfeOGF/cBNSEgIw90Cj1KgNWgWDWhVK+vO0MQW13Ws1pBc2QyjAnPmzDFBa6cej0BrKPhoQMsusKfxV47NslsmIToKVFVVYdmyZdi5c2d0EuDhrgKtQZjf78jDgKkrDEfCu8lxWba0nryc1O/hTYXE7jQFBNrTJTZp0iS9O3TVVVdh165dTitLSW+cKCDQAnj//fd1YJW18Oqrr46TKhDf2aQtYdasWY4SQaAF8Nhjj/WDlvBO2bgHKfWd6O7tc1ShSmLPKECnlWnTpvX70F7A4EQLvUAL4MUXX3QL7YCZiRjwdqr2uXj+PtyxvgDP7a7C0uIW5LedWTjtTBWRLbspQAv8oEGDtKEzNbTGb/p3M9AQqAC2W9o9pUegBVBUVITzzz/fBO7TTz+Nqq5j+LiqA/+3/yDG7yjHratzcdG8dB1kAj34/f0Ys7UEr2TUaec29hz3pLUcj4ICHKrxNFzDVpjQOi0ItKdLLDc3V+sqPfDAA3j33Xc9lmPvyZPY33wYy4pb8FJaDe7bUowrlmWbQP78nL24eVUufplcgTl5jdjb2I3ePnutyuAxgzH2A6Fka+su0K/bib7dAq270gziGFvYpNpDePtAA371aQX+c10+vrwwwwTzVxdl4p6PCvGH1GqsKm1F2aFTzulB3E4u8UMBDpnRNqFmSrlewvFxT8NtrufaaV+gDXNpFLT3YHVZK/53Xy3GbivBdStycO47aTrMA99OxdXLs/FQYile21+PHbWH0H40/KsyhDnbtoheOadMnDjRZIhS85LdeaHZIuE+EhE30LKgkpOTfcgRmZ8P9/Zhz8EuzMtvwqSUKty9sRDfWJKlg8xnZRq+frg2D8/uqsSigiZktxyOTOJi6C6ejFAKWqdmNW6gpcWQXSU7/7tWdx3Dpsp2zMyqx6OflGnPxRckmA1f//b+fty7uQh/TK/Fhoo21HTF3iLhVsHEMvdkhLLqHtGIJy6g5TMNzf7enm+iIb6/98xqPoz3iprxYmo1Rm0uwr8v3W9qlb8wZy9uXHkAj+8ow1s5Ddh9sBM9MraslbknI5S/2tvxvLiAlku4sPBoSXSitdBdxWk72ovtNYfwRk4DfplcrnWlL5m/zwTzpYsyMXxDAX63p0qzdhfE0dgyu8BO/ZN2V97GYzEPLQfR2crSSsjuUiz+8xoLtKTjCFaWtmrd559uLcE1H+Tg7NlnDF9nzU7VjvG3VzPrsLW6A00xOLasjFBGbWJlO+ahNY7Txeozjq/KeKzvJFIburQxYxq22Pp+bXGmqVX+59OGr6c+rUBCXiPSm7px4qRzx5bpnsiW1vWjPKF8aWbn32MaWnaFVSvLQmArS3AlnFLg4OHjmuGLLe4vtpfiuysPgM/HynVTeXyN3FykOZJw6KrcIWPLNDjSluH6ceK4rGt9jVloWThc9WHUqFHaUA+He/jyKlkJwrUK9N/Pbe3BksJmTN5TjR9vKsK33jcbvs5L2IubVubikU/K8Pr+g0iqO4SOYzK23F/J8ByJWWjZqrp2jdR+eKSM7Vg7j5/Ap3WdeD37IP4nqRy3rcnDxfPMhi92ue/aWIBJKZVYXNiMHBlbDkuliEloaTlki+r6/MKuEsG181htWEo5jJFWdh7FmrJWTE2rwQMfF+PK5WY/bBrBvv1BDh7cVoLp6bX4qLIdtd0ythxKkcQktPQpdTd7g11mQkt4JYRPAZqvMpq6MTevEc/srMAd6/PxFRc/bA5P3b42H09+WqH5a9ND7MgJmbfsT6nEHLRqfM61lVViENpYGatVeXLKd/ORXmyr7sCrGXX4eWIprv/wAD73rtnwRccROpBwUsUHJS0obHfGC6gjWQYxBy2B9Oa6xlbYE9CRFF7udUaBovYjWF7cojmBcBbU5S5+2OcnpGsunXTt/FtWvQY+/wDiNcQctPFakLGWb3aV2WWmWybdM7+3OheD5pr9sH9GcNQAAAOzSURBVL+xOFObbPHb3VWYn9+kdcnjYdqyQBtrtT3G80Mj1saKds3j694txRiy1Gz4OuedNFz7QQ5+tq1Emw65pqwNFZ2xNW9ZoI3xSh4v2ePwEqcw/npXJYauy8eXFpgXIPjiggztOBco4EIFHL7qdOjYskAbL7U6DvNJhw+uJsLFBWj4Ygv8D4YFCOjxNWTpfrDFfim1RptUcaDV/gv2CbRxWJnjPctc5ofL/XCqIxcg+LqLH/YFc9Nxy6pcPLajTAOei/vVd9tnwT6BNt5rsORfU4CTI9IbuzEntxFPJJdrbpq0Whv9sC9bkoUfbSzUltFdUNCEtIYuHD0R+UkVAq1UWlHAiwJcsI8t7Z8z6jSPLy6ZawSZ3W2u+zU2sQQz9tVhbXkbijvCO7Ys0HopMPlJFPCkABerX1rUAg43ceVNTm00wvzlBRna8ad3VmD2acNXi0VjywKtp1KR46JAgApwwT6+RuaNnIPaDCj6XHPRASPM/7EsW1sre0paDZaXtAQ1qUKgDbBg5HRRIFAFuGDf+vI2vLy3RpvqyGWAjCBfODddcx4Zv6NMe5sFVxNxt2BfX18fJkyYgHO+cD4u+srXMGPGjECTEtL58qbkkOSTi2NBAS7YR4MWu9C3rs4D30xhhJnunHTr5BpfCwua8OOfPdxvuqm3t2FYrZFAa7WiEl9MKMAF+z6pOaQto0uvLo4j6yAPPKsftMOHD49YvgXaiEktN4oFBbhg3+fOO68ftCNGjIhY9gTaiEktN4oVBZ555pl+0L733nsRy55AGzGp5UaxpADfpTx48GDcfPPNmDNnTkSzJtBGVG65mSgQugICbegaSgyiQEQVEGgjKrfcTBQIXQGBNnQNJYYYUUAtOKiW+FXffAeVnYJAa6fSkLREVQH13iHXtyHYbalfgTaq1URubicF1Bsd7ZQmd2kRaN2pIsfiUgGnvBhOoI3L6imZdqcAXxLnhLW4BVp3pSfH4k4Btbi+Mj6pbzu+R1mgjbvqKRl2p4AnIxRhtlsQaO1WIpKeqCjAl1/bbWjHkxACrSdl5HhcKUAjFF9V44Qg0DqhlCSNYVeAz7BOMEJRCIE27NVBbmB3Beg8QWhnzZqF5ORk/WM3pwqlo0CrlJDvuFWAHlDsHrt+7PpWR4E2bquqZNypCgi0Ti05SXfcKiDQxm3RS8adqoBA69SSk3THrQICbdwWvWTcqQoItE4tOUl33Cog0MZt0UvGnaqAQOvUkpN0x60CAm3cFr1k3KkK/D8kG625vZ5n1AAAAABJRU5ErkJggg==[/img][br]
A polygon has a perimeter of 18 units. It is dilated with a scale factor of [math]\frac{3}{2}[/math]. What is the perimeter of its image?
Solve the equation.
[math]\frac{4}{7}=\frac{10}{x}[/math]
Here are some measurements for triangle ABC and triangle XYZ:
[list][*]Angle [math]CAB[/math] and angle [math]ZXY[/math] are both 30 degrees[/*][*][math]AC[/math] and [math]XZ[/math] both measure 3 units[/*][*][math]CB[/math] and [math]ZY[/math] both measure 2 units[/*][/list]Andre thinks these triangles must be congruent. Clare says she knows they might not be congruent. Construct 2 triangles with the given measurements that aren't congruent. Explain why triangles with 3 congruent parts aren't necessarily congruent.