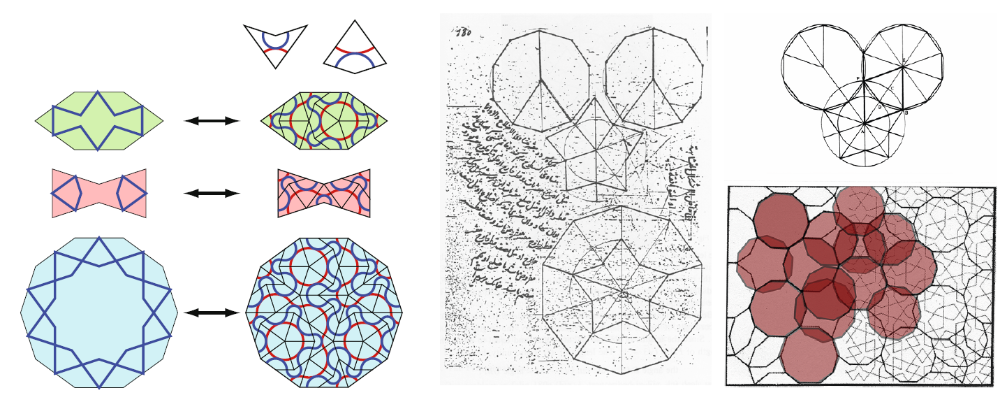
girih tegels en Penrose
je methode bepaalt mee je resultaat
Werk je met passer en liniaal, dan teken je gemakkelijk regelmatige patronen met 2-, 4-, 6, 8 of 12-voudige symmetrieën. Vijfhoeken en tienhoeken zijn mogelijk, maar liggen al minder voor de hand. Maar wanneer je vrij vormen aan elkaar kunt plakken, dan denk je ook vrijer. [br]Wanneer je girih tegels gebruikt, heeft de keuze van vormen en hoeken zijn gevolgen. Lu en Steinhardt suggereren dat bijna 800 jaar eerder de islamitische bouwers tot een gelijkaardig resultaat kwamen als Penrose, met name dat ze niet-regelmatige vlakvullingen creëerde,.
Lu's verhaal wordt helemaal mooi wanneer je merkt dat je zonder probleem Penrose vliegers en pijlen op girih tegels kunt plaatsen. Pas je dit toe op een girih patroon dan krijg je zelfs een perfecte Penrose betegeling waarin de pasboogjes mooi doorlopen. Voor het mausoleum in Maragha klopt dit op enkele zeldzame 'foutjes' na en zelfs die kan je gemakkelijk corrigeren door een zeshoek en een strik van plaats te verwisselen. Volgens Lu is het ook mogelijk dat deze fouten 'slechte reparaties zijn'.[br]De insteek van Lu is die van een 21e eeuwse wiskundige die, 800 jaar terugkijkend naar het verleden, de plakregels van Penrose wil toegepast zien en afwijkingen dus maar toeschrijft aan foutjes of misschien slechte reparaties.

hoe 'Penrose' zijn de Islamitische geometrische patronen nu?
Het artikel van Lu en Steinhard zorgde niet alleen voor een wereldwijde hype, ook mensen die zich al langer verdiepten in Islamitische geometrische patronen kropen in de pen en kaderden de claim zowel in een wiskundige context als in een bredere culturele context. [br]Islamitische ontwerpers creëerden geen patronen die in principe oneindig doorliepen maar werkten binnen een beperkte context als een boogveld boven een poort. Wat je dan ziet geeft vaak een andere indruk dan de theoretische oneindige betegeling waarin je deze context kunt plaatsen. De claim van Lu en Steinhart oogt dan heel anders. [br]In een laatste hoofdstuk [url=https://www.geogebra.org/m/cyjb6gsb#chapter/408538]commentaar en argumenten[/url] gaan we hier verder op in. [br]Zo verwijst Carol Bier naar de wiskundige kennis en het onderzoek van de eigenschappen van (overlappende) tienhoeken in de periode waarin de Gonbad-e-Kabud gebouwd werd. En ja, in overlappende tienhoeken verschijnen nu eenmaal zowel vliegers en pijlen als girih tegels.