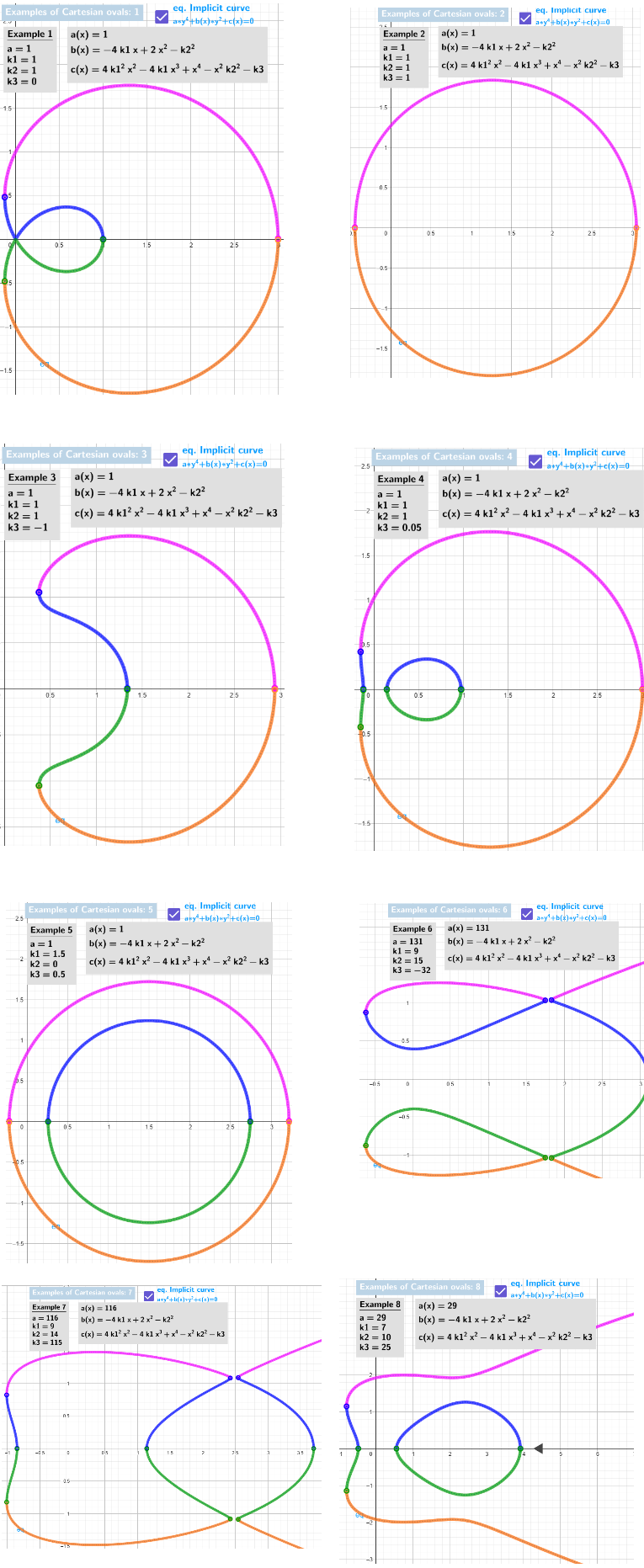
[size=85][b]Fig. 1:[/b] [b] Examples 1–8 (from [url=https://www.geogebra.org/m/cgfbcxau]applet[/url]) of Descartes' ovals are composed of sections of complex functions taken at specific intervals.[/b][/size]
Images: Branches of an implicitly defined biquadratic curve found using complex functions: Cartesian oval
Images made with [url=https://www.geogebra.org/m/cgfbcxau]applet[/url].
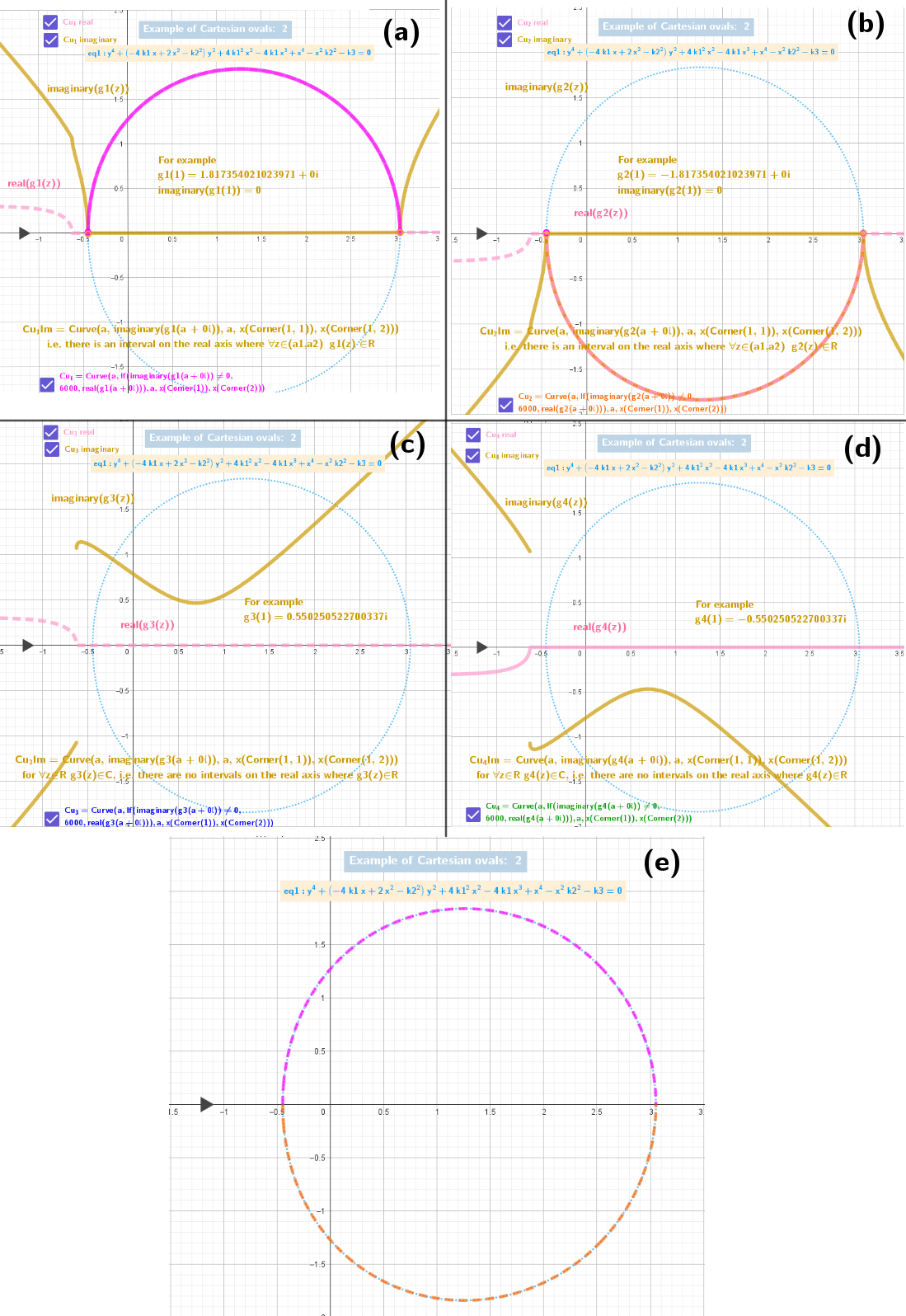
[size=85] [b]Fig. 2: [/b] Example 2 of Examples 1-8 of the applet under consideration is notable in that the functions [b][color=#0000ff]f3(x)[/color][/b] and [color=#6aa84f][b]f4(x)[/b][/color] are not defined in the real domain.[br] Figures a–d show the complex functions [b][color=#f6b26b]g1(z)–g4(z)[/color][/b]. Note that the functions of the[color=#f6b26b] imaginary parts[/color] of the complex functions [b][color=#f6b26b]g3(z)[/color][/b] and [b][color=#f6b26b]g4(z)[/color][/b] do not have intervals on the x-axis where they are zero.[/size]