IM Geo.3.6 Lesson: Connecting Similarity and Transformations
What’s wrong with this dilation?
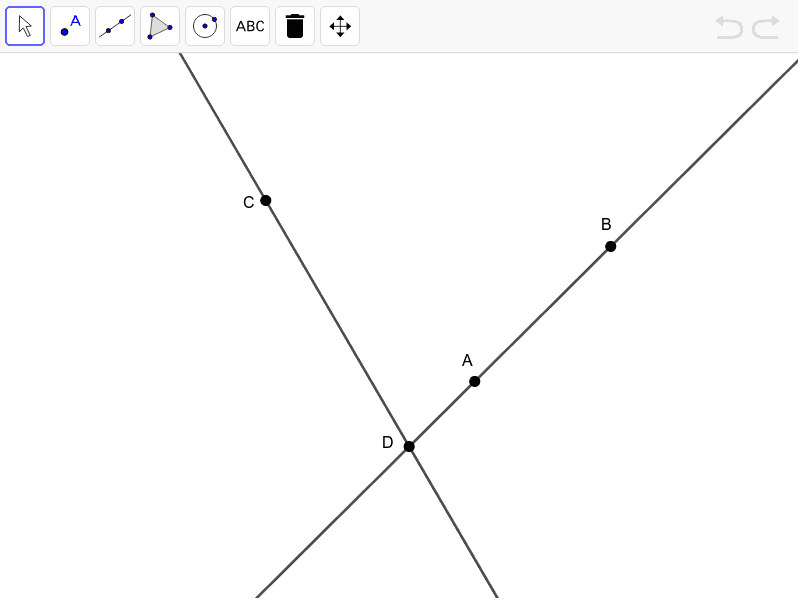
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAhEAAAFLCAYAAABoY94eAAAgAElEQVR4Ae2dB5QURdeGP0AyguSsBAUElKwgAhIk55wzSEYyCCggOYkkiZKjZMlJkmSVIDlIUknykTPc/7z12/PNDrO7M7sTqrvfe86c2Z3prq56qqf77apb9/5HaCRAAiRAAiRAAiQQAQL/icA+3IUESIAESIAESIAEhCKCJwEJkAAJkAAJkECECFBERAgbdyIBEiABEiABEqCI4DlAAiRAAiRAAiQQIQIUERHCxp1IgARIgARIgAQoIngOkAAJkAAJkAAJRIiA30TE5s2bpXTp0jJ9+nS5d+9ehCrHnUiABEiABEiABPQl4DcRsW7dOqlVq5b85z//kezZs8uAAQPk5MmT+pJgzUiABEiABEiABLwi4DcRYdTi999/l65du0qSJEkkUaJE0qpVK9m6davxNd9JgARIgARIgARMSsDvIsLgcufOHfn2228lV65canSiQoUKMmfOHHny5ImxCd9JgARIgARIgARMRCBgIsKZybJly6RixYpKTOTOnVuGDh0q58+fd96Ef5MACZAACZAACWhOICgiwmBy8OBBadeuncSNG1dSpEghHTp0kF27dhlf850ESIAESIAESEBjAkEVEQaXa9euybBhw+Tdd99VoxPVqlWTRYsWGV/znQRIgARIgARIQEMCWogIZy7z58+XkiVLKjGRP39+GT16tFy5csV5E/5NAiRAAiRAAiSgAQHtRITBZOfOndKsWTOJFi2apE2bVrp06SL79u0zvuY7CZAACZAACZBAkAloKyIMLhcuXJB+/fpJunTplKCoU6eOLF++3Pia7yRAAiRAAiRAAkEioL2IMLi8fPlSvv/+eylUqJCa6ihcuLCMHz9erl+/bmzCdxIgARIgARIggQASMI2IcGayadMmqVevnhITGTNmlF69eslvv/3mvAn/JgESIAESIAES8DMBU4oIgwnCaPfs2VMtD40dO7Y0atRIVq9ebXzNdxIgARIgARIgAT8SMLWIMLg8ePBAJkyYIPny5VOjEyVKlJApU6YIomTSSIAESIAESIAE/EPAEiLCGc2qVaukatWqSkwg7sRXX30lx44dc96Ef5MACZAACZAACfiAgOVEhMHk0KFD0rFjR0mQIIHEjx9fmjdvLhs3bjS+5jsJkAAJkAAJkEAkCVhWRBhc/vnnHxk1apRKR4605GXLlpWZM2fK06dPjU34TgIkQAIkQAIkEAEClhcRzkwWL16sRATERI4cOWTQoEFy5swZ5034NwmQAAmQAAmQgIcEbCUiDCZ79uyRzz77TGLGjClJkiSRNm3ayLZt24yv+U4CJEACJEACJOABAVuKCIMLcnIMHDhQ3n77beWIWalSJZk3b57xNd9JgARIgARIgATCIGBrEeHMZdasWVK0aFElJrBUdMSIEXLx4kXnTfg3CZAACZAACZCAEwGKCCcY+POnn36Shg0bKjGRKlUq+fzzz2X37t0uW/FfEiABEiABEiABiohQzoGzZ89Knz59JE2aNEpQ1KhRQ3744YdQtubHJEACJEACJGA/AhQR4fT5kydPZPLkyVKgQAElJgoWLCjffvutXLt2LZw9+TUJkAAJkAAJWJsARYQX/bt27VqpWbOmEhNITd69e3c5ePCgFyVwUxIgARIgARKwDgGKiAj05dGjR6VLly6SOHFiiR49usoounLlygiUxF1IgARIgARIwLwEKCIi0Xe3b9+WMWPGSM6cOdXoxCeffCITJ06Uu3fvRqJU7koCJEACJEAC5iBAEeGjflq2bJlUrFhRiYlMmTIpp8wjR474qHQWQwIkQAIkQAL6EaCI8HGfHDhwQNq2bStx48ZVryZNmsi6det8fBQWRwIkQAIkQALBJ0AR4ac+uHr1qgwdOlSyZMmiRidKliwp06ZNk+fPn/vpiCyWBEiABEiABAJLgCIiALwRSvvTTz9VYiJ79uwyYMAAOXnyZACOzEOQAAmQAAmQgP8IUET4j+0rJe/YsUOaNm0qUaNGlYQJE6okYFu2bHllO35AAiRAAiRAAmYgQBERhF66cOGC9OvXT9566y01OlG+fHmZPXt2EGrCQ5IACZAACZBAxAlQREScXaT3fPHihUyfPl0KFSqkxESuXLlkyJAhTPwVabIsgARIgARIIBAEKCICQdmDY2zcuFHq1q2rxETy5Mmlffv2snPnTg/25CYkQAIkQAIkEBwCFBHB4R7qUU+cOCE9evQQCIn//Oc/UrVqVVm4cGGo2/MLEiABEiABEggWAYqIYJEP57j379+X8ePHS968eZWY+PDDD2XUqFFy48aNcPbk1yRAAiRAAiQQGAIUEYHhHKmjrFq1SqpUqaLERNq0aVXejr1790aqTO5MAiRAAiRAApElQBERWYIB3P+3336Tjh07Svz48dUy0dq1awvCbdNIgARIgARIIBgEKCKCQT2Sx7x586aMHDlSELgKfhNY3TFu3DjBFAiNBEiABEiABAJFgCIiUKT9dJxFixZJmTJllJjIkCGD9OzZUw4dOuSno7FYEiABEiABEvgfAYqI/7Ew9V+7d++Wli1bSowYMSRWrFjSsGFDWb16tanbxMqTAAmQAAnoTYAiQu/+8bp2ly9flq+//loyZsyoRieKFy8ukydPlpcvX3pdFncgARIgARIggbAIUESERcfk382aNUuKFi2qxASyiX755Zdy6tQpk7eK1ScBEiABEtCFAEWELj3hx3ps3bpVTW/ACRMrO5o1ayYbNmzw4xFZNAmQAAmQgB0IUETYoZf/beOZM2ekd+/ekjp1ajU6AYfMGTNm2IgAm0oCJEACJOBLAhQRvqRpkrIeP34skyZNkvz58ysx8f7778vAgQMF/hQ0EiABEiABEvCUAEWEp6Qsut2aNWukRo0aSkwkTpxYWrduLT/99JNFW8tmkQAJkAAJ+JIARYQvaZq4rKNHj6pw2okSJVKColKlSjJv3jwTt4hVJwESIAES8DcBigh/EzZZ+bdv35YxY8ZIzpw5lZhAArDhw4cLomSa2f744w9p3LixvPHGG6pdcDJNly6d+szM7WLdSYAESCCYBCgigklf82MvXbpUKlSooG66KVOmVHk7zJj4C86jEA1FihSR5cuXq+kaTNl888038tVXX2neC6weCZAACehLgCJC377Rpmb79++XNm3aSJw4cdTNuHr16rJ48WJt6hdWRSAWICAaNWoU1mb8jgRIgARIIAIEKCIiAM2uu/z9998yZMgQyZw5s7oxf/TRR2rq4+HDh9oiyZEjhxqB0LaCrBgJkAAJmJgARYSJOy+YVYfTZYkSJZSYeOutt6Rbt25y+PDhYFbplWMjdTpGIbja5BU0/IAESIAEfEKAIiIUjHAwpIVPYMeOHdK0aVOJEiWKvPbaa1K3bl1ZsWJF+DsGYAv4OyRIkCDEkeBguW3bNsfrv//9b4jv+Q8JkAAJkIDnBCgiXFhdvHjRkVo7duzY6gnbZRP+64YAbs64aWNUAk//n3zyiUycONHNloH7CI6UeDkb6oj6GS+MVtBIgARIgAQiRoAiwoVbqVKlHDcY40Yzfvx4l634b2gEnj9/LtOmTZOPP/5YcXznnXdUqG2E3A60uRMRRh2MFRvG/3wnARIgARLwngBFhBOzW7duvSIgICQ+/PBD+eyzz2TAgAEq1wSGwzFigfDRtNAJIMlXnTp1FFOs7ECchnXr1oW+g4+/QcAs15EI4xBYrRHad8Y2fCcBEiABEgibAEWEEx88RUePHv0VIVGwYEGpWLHiK58bIxWvv/66ZM+eXTkaNmjQQE2BjB49WubPn6+c+k6cOCE3btxwOpK9/jx+/Lh0795dkiVLphh++umnMnXqVL9DQBwI9JE7x0qs2ujYsaPf68ADkAAJkICVCVBEuPRup06dXhELeKJ+8OCBXLhwQQ4ePKiepmfOnCmDBg1SKbbfe+89qVy5skBsYPmjETraEBnO7/CzyJAhg2B5ZLVq1aRt27Yq+RWmAJDHAjEZzp8/L/fu3XOpmfn/RZswNZQnTx7FOFu2bNK/f3+5cuWKXxoHp0n4aCBKJfoL/g8QFHD8RJ8g8BSNBEiABEgg4gQoItyw+/bbbyV9+vSCoEoQEGHZkSNHZMKECa9scv36dUE+Cty0EJgJToa4YbZr105q164txYsXFzwNp0qVyu3ohyE8UqRIoUJQI213kyZN5IsvvpCxY8fKokWLZMuWLWpZ5Z9//ilPnz59pQ46f7By5UqpUqWKupnjJt+yZUu1YsLXdYaQwNQFVmkYTPE3pjrgDEojARIgARKIOAGKCDfsNm7cKPny5ZOdO3e6+TbkRz///LPMnj075Ide/vfkyRPlY7Fv3z5ZtWqVTJ8+XYYNGyZdu3ZVfgTlypVTfhkYwcDUiXEzdH2PHz++ZMqUSc3116pVSz7//HMZOnSocnTE0/euXbvk5MmT8s8//3hZQ/9t/uuvv0qHDh0EdUd70NZZs2b574AsmQRIgARIwGcEKCLcoPz+++/VDQ3TCuHZ+vXrAz4sjqdr+FlglGPBggWCkZM+ffpIq1at1BRJ4cKFJWvWrJI0aVIVv8FVbOB/xHRIkyaNEkvIj4GRgN69e6t8EnPmzFFTNgcOHFBTOPfv3w8PQ6S/h8/IiBEjBFMcqF+uXLlUdEw4u9JIgARIgAT0JGArEYGbrnOgIfztLk7A119/rW5knoRz/uGHH2Tz5s169q6IvHz5Uv766y/BE//atWsFAmnw4MHKqbBevXpSsmRJyZ07t6RNm1ZixYql2u1OdMDPAzd4TMMgoBRGD7BaBdM0mK7ZunWrmr5BaOxnz55FisfChQuldOnSqi5wxsQUEHxFaCRAAiRAAnoRsI2IgIBwd3N0t8yvdevWaltPugo3ZSvd4OBAeu7cOcE0DbJ4wt+jb9++0qJFC7VCBQ6hiP3gnFLblSvECNJs58+fX2UBhS8HwmJjigZTNfCHQPmnT5+WsEYasA2Oa6yYgQ8FRl5gEC8FChRQIxYDBw70pKu4DQmQAAmQgI8J2EZEYLmfawjk0Fhi1QTiGnhimErA1IJd7ebNm/L777+r0Zi5c+fKyJEjlS9H/fr11ZJXrFyBcyimT1zFhvE/RhswygFBB2dWiAXE5UB0ycmTJysfCQg7IxomBIqxr/Heo0cPu3YB200CJEACQSNgGxHhTXAh+BSkTp3ao07BU7C/lih6VAETbYRpjsuXLwt8LX788UcVKwJTR1jmCuGGJbIZM2YMU3Bg9AHLZA3xYLwnT57cRCRYVRIgARKwBgHbiAg8xeLJ1hPDUzGCR3lieAK+c+eOJ5tyGw8IwImzS5cuasu7d++qKQ8k+YKzJwQbpo/QN4Z4MN4x0sG4Dx4A5iYkQAIk4EMCthARWM2Am42nNxkMl0N04Am5Z8+eKqgUYjMg38KSJUtU7Ijdu3crR0JEqITzIs03BOCY2a9fvzALwyoOQzwY73HjxlWfIWcH+opGAiRAAiTgfwK2EBGhOVVCFLgzzNF37txZEAYbAuTSpUty7Ngx2bt3r2zatEmWLVum5ulHjRqlnozdlcHPIkYAzpbgGp59+eWXkjBhQhU3A2Lv0aNH8t1336l4GhAWiKkBAQgnURoJkAAJkIB/CNhCRBgpqj1BiHgFUaJEUTELPNme2/iWwC+//CJTpkwJt1BE6Gzfvr0KZ+26McKH16hRQ41MxIwZUzBahHgeNBIgARIgAd8SsIWIQIhjvDwxrLTAkyzm4GmBJ4DYHcYyzrCOjlDf6CfEqgjNEJIcI0pGLpNixYrJpEmTQtucn5MACZAACXhJwBYiAks7PXWqhBMfbk46B5Dyso9NtTlWbWAkITw7fPiw6ick1grPMCWFJb7IVYK+RZI0xL5AEC4aCZAACZBAxAlYXkQgyRJuHPCL8MTg74DtEfuAFngCSJ8OIReeQeShn7Zv3x7epiG+h2Ns+fLl1b7IQ9KsWTOPjheiEP5DAiRAAiSgCFheRGBFBm428Ph3foUmKhDcCNvrlKTKTucq+LsLRe7KACMQ6KczZ864fuXR/0h2hgBWRswJhNnG8lEaCZAACZCA5wQsLyKwAgOREF1foa3MQCwC3JxowSGA5Ztnz54N9+BGP0U2ORimNIYMGaKyn6LfEWETAbBu374dbh24AQmQAAnYnQDvli5nANJnx4gRw+VT/hsoAshG2r9/f7VCAw6Wq1evVlMWSCCGUYerV68K8ntgWaevxR7CdpcoUUKVC2dMZEVFdE0aCZAACZCAewIUES5ckNkSgaZowSEAkQCxANEAfweICIgJTHMgLwccZLHi4u2331ZZR/1RSxwXScOw1BdCpWLFih6tGPFHXVgmCZAACehMgCLCpXdKlSqlAha5fMx/NSOARF0QEv608+fPC4Javfnmm0pM5MmTR2UiffLkiT8Py7JJgARIwDQEKCJcuip37txSuXJll0/5r24EihYtqvxcAlEvJA6bOnWqShCGkQlkJe3QoYOKYhqI4/MYJEACJKArAYoIl57BUyfmwml6E0ASrlq1agW8koh8Wbt2bTUyAUGBEZEVK1YEvB48IAmQAAnoQIAiwqkXHj58qJb8wbGPpjcBjAbACTZYhlwq3bt3F+RZgZhAinIEtKKRAAmQgJ0IUEQ49bYRmApOfDR9CSCGR7Ro0WTo0KFBryTSlY8bN07gLwExgZGsrl27CvwpaCRAAiRgdQIUEU49vH//fnUjWLVqldOn/FM3AqdOnVL9NGvWLK2qhmkN+NNATEDk1KlTRzZu3KhVHVkZEiABEvAlAYoIJ5pr165VNwDGBnCCouGfu3btUv20YcMGDWsngkykyDCKsNoQFAh0NnHiRC3rykqRAAmQQGQIUEQ40cOTLS76ly9fdvqUf+pGAE/86Cdk6dTZrl+/LsOHD5esWbOq+mJJ6hdffKECZulcb9aNBEiABDwlQBHhRGrUqFHqYv/o0SOnT/mnbgSw3BIiAjdpsxgCZiE/B+qNfB2NGjWSnTt3mqX6rCcJkAAJuCVAEeGEpWfPnuoi7/QR/9SQAHJd4GZsRsNUTIsWLSR69OiqDZ9++qmElsfFjO1jnUmABOxFwJxXYj/1EdJCJ02a1E+ls1hfEUDY69dee81XxQWlnIsXL8qAAQMkQ4YMSkxgygNZZu/cuROU+vCgJEACJBARAhQRTtQqVaok77//vtMn/FNHAg0aNJA0adLoWDWv6/Ty5Us1EgHnS4yuJEiQQI1UwDmTRgIkQAK6E6CIcOqhjz76SEqWLOn0Cf/UkUCZMmUkX758OlYtUnXavHmz1K9fX4kJCIqyZcvKokWLIlUmdyYBEiABfxKgiHCimylTJuXw5vQR/9SQQN68eaVChQoa1sw3VUIcDKziSJkypRIUOXPmlMGDBwtyeNBIgARIQCcCFBFOvZEwYULp0aOH0yf8U0cC6dKlk5YtW+pYNZ/WCWHYv/vuO5VVFiMT8Ndp27atHD9+3KfHYWEkQAIkEFECFBH/ksNyQVyox4wZE1GW3C8ABJCGO27cuPLVV18F4Gj6HGL16tUq2RfOUbwQGZORVfXpH9aEBOxKgCLi355H4CJcnBcuXGjXc8EU7caqBvQTntDtaIcPH5ZOnToJRs3A4YMPPpDRo0fbEQXbTAIkoAEBioh/O2Hr1q3qorx9+3YNuoVVCI3AwYMHVT/ZPf32rVu3lHjAaiKIidSpUytxceHChdDQ8XMSIAES8DkBioh/kcILHhfjkydP+hwyC/QdgfXr16t+2rt3r+8KNXlJP/zwg5QrV05xwTlcs2ZN2bRpk8lbxeqTAAmYgQBFxL+9NGHCBHURRpppmr4E5syZo/qJT9yv9hGEVevWrSVWrFiKUcGCBW077fMqHX5CAiTgDwIUEf9SRbRAPMXR9CbwzTffqH66f/++3hUNYu3+/PNPtSQUS5ZxTqdPn16tOrp27VoQa8VDkwAJWJEA75r/9mq7du2U178VO9lKbUL8BIo9z3sUIzfFixdXzGLEiKGCWf3888+eF8AtSYAESCAMAhQR/8KpVauWIFUzTW8CiA+ROHFivSupYe22bdsmjRs3VmICIqxo0aIya9YsDWvKKpEACZiJAEXEv71VrFgxKVSokJn6zpZ1rVKlimTLls2WbfdFo8+dOyd9+/aVtGnTKkGROXNm6dOnj9y7d88XxbMMEiABmxGgiPi3w7FUrkaNGjbrfvM19+OPP5YSJUqYr+Ka1fjp06cyZcoUQb4YjEzEixdPmjZtKr/++qtmNWV1SIAEdCZAEfFv7yBPQYcOHXTuK9ZNRLJkyaLm9QnDdwTWrVsntWvXdkx1lCpVShYvXuy7A7AkEiAByxKgiBCRR48eSfTo0ZVHu2V72iINgz9Et27dLNIavZrx+++/K7bI0YHRiezZs6vfxPPnz/WqKGtDAiSgDQGKCBE5f/68umjOmDFDm45hRV4lgBgeuLmNGjXq1S/5ic8I3LlzR8aOHSu5c+dWvBMlSiStWrViIDafEWZBJGAdAhQRIrJ79251scSwLk1fAseOHVP9NH/+fH0rabGaLV++XCpVqqS4Q8AhBTuSgdFIgARIAAQoIkRk5cqV6iJJpzK9fxRYpogbGfKc0AJLADlLEEsFDpjoA4xSIPAXjQRIwN4EKCJEZPr06erCeOnSJXufDZq3HjkicAM7fvy45jW1bvUQ9XL48OGSNWtW1RfJkyeX9u3bC7Kr0kiABOxHgCJCRIYOHaouiHCwpOlLAOm/ISKuX7+ubyVtVLMFCxYIVnKgT/CqVq2abNmyxUYE2FQSIAGKCBHp2rWrRI0alWeD5gQGDBigblYvX77UvKb2qt6uXbukefPm8tprr6n+yZ8/v0yePNleENhaErApAYoIEWnUqJGkSpXKpqeAeZqNOB6xY8c2T4VtVlNkVu3fv79K+IWRCUTFhEC/ceOGzUiwuSRgHwIUESJSrlw5yZMnj3163aQtrVOnjmTIkMGktbdPtV+8eCHff/+9FC5cWI1MRIsWTdB3e/bssQ8EtpQEbEKAIkJEPvjgAyUkbNLnpm0mwl0jTDPNPAQ2bdqkIowafhMQFrNnzzZPA1hTEiCBMAlQRIio4VfM6dL0JpAzZ07lvKd3LVk7dwROnjwpvXr1EoSXh6DImDGjfPnll3L//n13m/MzEiABkxCgiBCR119/XWUyNEmf2baaqVOnlrZt29q2/VZo+IMHD2TixIlq9A9iIlasWNKwYUM5dOiQFZon//3vfwXxTPBOIwE7ELC9iIDTFy5mEyZMsEN/m7aNyDoZM2ZMGThwoGnbwIqHJPDjjz+qkSVjqgPTVUuWLAm5kcn+g5M22vPTTz+ZrOasLglEjIDtRcSRI0fUj37ZsmURI8i9AkIAwYxwcZ42bVpAjseDBI4ARiE+//xzeeONN1Qfv/vuuzJkyBAx21Le3377TdX/rbfeYjTPwJ0+PFKQCdheRGzcuFH98LHWnaYvgX379ql+WrNmjb6VZM0iRQAJ1pBc7b333lN9HT9+fBV/4vTp05EqN1A7FylSRC0Xx/tXX30VqMPyOCQQVAK2FxHz5s1TFyw4ftH0JYChb4xEHDhwQN9KsmY+I7B48WK1YsqY6ihbtqzoLCAxfYG6/vHHHyphGZKW0UjADgRsLyLGjBmjfvw3b960Q3+bto1I046LNAIa0exDALElkIYcDpjo/xw5csi3336rHQDUC/4QMIxCYDSCRgJ2IGB7EdGnTx91cbJDZ5u5jUj6hJuIVZYEImNs9+7dVWbM9evXm7lrAlL3K1euyKBBg+Sdd95R50GSJElU4q/Lly8H5PhhHQQCN0GCBI4VGRAR8O+gkYAdCNheRHz22WeSMGFCO/S1qduIGy5EhBUMSarQFufX+PHjrdC0gLQBwaqKFSvm4Iepg2CuhoAjJWKY9OvXT70aN25smXM1IB3Kg5iagDWuypHoAmQehDc4TW8CTZo0kRQpUuhdSQ9rV7VqVccN0BASDOftITynzSAcjCWV4JgvXz6ZMmWK0xb+/xOjDhiFwPSF8cLUBuqD1Ro0ErA6AduLCIThxVMNTW8CFSpUUE97etfSs9rlypXrFRGBm06tWrUEeSYSJUqkcoQY4dgRTRXRHVetWiX79+8XDOEzbf3/WJ89e1YFi0PCL3BEMj2MXGG1hz8NAaUwbeG6EgOfox7BHB3xZ7tZNgk4E7C9iMiaNavUrVvXmQn/1pAA0kuXKVNGw5p5XyVjagY3GuOFtq1evVomTZokffv2lRYtWigv/4IFC6qRMjztJk2aVKJEieLYB/viMyyJLFmypIr8iLK/+eYbWbBggYqcePz4cbl+/brpYi54T1XkyZMnKgU58qsYXGvUqCF79+6NSHHh7tOxY0fBVIa76JQ4PvqBRgJWJ2B7EYGLcJcuXazez6ZvH3ItNG3a1PTtQAOePXsmFStWdNzokEEWN/uwrE2bNoLsmFhFhG23b9+uojt+9913MmDAAOVkWLt2bTWqBlGBqR+Mahg3U7zHiRNH5ayAMKlevbpy6oSz4vTp09XyScTiOHfunNy5cyesqpjiu7Vr16qRHaP9aPPcuXN9Vncs5UTZcKp0Z5jScB2hcLcdPyMBsxOwtYjAkDAuBCNGjDB7P1q+/ngS/+KLLyzVTtz8f/jhh3DbdO/ePenWrVu427lugJUsZ86ckZ07dwoisk6ePFmFDe/QoYNKzY0w07jZYfg/evToIQQHfhdIloWpF8RogIDr3bu3jBs3ThYuXCibN29W+S6wauLx48euh9bm/6NHj0rXrl0FqznQpnTp0innx4cPH0aqjpiqCEskQFwsX748UsfgziRgBgK2FhHG04Qvn1DM0Olmq+OtW7fUDQA3MKsYphhwU0Nmy/Dsr7/+UqMN4W0Xme+fP3+ufC3gc7Fy5UrloIhRCoSjrlevnpougaBIkyaNymGCuju/IPIyZ84sn3zyiWBEpFOnTjJ48GBVDm6mEDInTpwQ5AXynHcAACAASURBVKoJht2+fVvFlzD8USCa0C6EvaeRAAlEnICtRcTu3bvVhXDDhg0RJ8g9/U7g2LFjqp88eWr3e2V8dABMSeAmjOmI8OzUqVPaza9DDOAGjN/OrFmzZOjQodK5c2dp0KCBlC5dWjBF8+abb0rs2LFDiA20GTdwOEHCcRTTOvD/gJhCyGss38RUBMTM+fPn5e7du+Hh8fp7jMpgWaghgiB8li5d6nU53IEESEDE1iICFxNcSBD4h6YvASOuAvwAdDYMb+OGZLzwFL9ixQq3VUZbcO6tW7fO7ffOHx48eNDUiccgBJD/Am3GVAiixPbo0UMtz8RUCZZmYpoBPhvGjd35PXHixJI9e3bB9AtGOdq1a6emJJB5d9GiRYLz4/Dhw/Lnn38q50pndmH9jRDqKCtevHjquJkyZZJhw4aF2AUiCc6uKJ9GAiTwKgFbiwhcHHCxunTp0qtk+Ik2BLDSAP2EEQmdDf4FRvIlCAojhoG7uXPc/DxtE+bfsb0dDCnf8XuEkycEGEZqwK9ly5aCZb4YvUifPr3jxu8sNvA3Rj4Qc+PDDz9UuTfQB3CcxkgJMsCiTCTbQ64cI9T91atXlXhAvBiUETduXDU64hzQCp9jeodGAiQQkoCtRcTAgQPVRSOyTlYhkfI/XxMYO3as6if4EehqRmwAV2c63MTwlO1qGLrHjQn+HuEZ4kNgiJ/2KoFr166pUQKEDoczI/ww4DiKpZ0ff/yxvP3224JsoGDt7oVRCDiQZsmSRbA0NHfu3JI6dWq322J/HI9GAiTwPwK2FhFY5x0zZsz/0eBfWhJAoCVcwF++fKll/VApjBagjnDWdTYjloDzZ/gb/gPY3hNDplk4JtIiRwBLVzECsW3bNrU6BX0Df4xy5cpJ3rx5lQ8HRAUcRI105Ogj59emTZsiVwnuTQIWI+DZVcxijTaaA+9sd0+Jxvd814NA69at1dOkHrVxXwsMuWOFgrMh7LG7iIbYBude1KhRBSmv4ReBIXY4KkKEYJgdgZMMw7TboUOHjH/57gMCyHOBaYzQ7Pvvvw8hHgwhgT7GSAf8L2gkQAI2d6xElD9EQqTpTQBD03g61Nng7Q/BYDhV4h3RDN35Q6AdiJKKYXQ4BWKefs6cOTJx4kQ1N4/MsnhKhmMmRmEQGApBoGi+IwA/iQcPHoRZIEYoDPGA9ypVqgjC5BuflS9fXo1qhFkIvyQBixOw9UgE5j9xYaDpTQA3ZDgs6mx4QnV2qsTfGOUKLX+CJwIWwdDgB0IB4dueR8RQrMrwxLBaA4G2nFdwbdy4UY0kGWICsSfgtEkjATsSsLWIwFp1DJXT9CaA5X1Y2qerGUHLXAUDRiEwOuHOcOOhgHVHxv+fwZnVkyBfqAlWbLz//vtuK4XgWT179lQhxiEokidPrv73xFnWbYH8kARMSMDWIiJWrFh+jwRownNCuyrj4oyhfV0NKzJwE3FNxGQ4W7pLCY3IjxSwwenRixcvypAhQzw6OKacihcvHua2CC+OmBWId2GMTlSrVk0FzApzR35JAhYgYFsRgYh7+MFPmTLFAt1o3SYgbgAcEF2DAOnUYow4IEaEq8GvAeeYq2FJMQWsK5XA/f/777/L+PHjwz0gEp4hZkT9+vXD3dbYAMtxq1at6hATiFcxf/5842u+k4DlCLx6hbNcE903CIl5cIF3Xdfvfmt+GiwCCDyEfkJoZV0N/g+IB2EYRh7g/Y96u3OsRDhnfEcBaxAL7PuePXs8Op/+/vtv1U+Irumt4RyAiISvDPoaI0/9+/fXOlmZt23k9iQAArYVEXCOwo+b6+/1/iEgciH6yZPw0MFqCern+sLKjNDSRBtt+vHHH4NVZVsfF799hLwPz4wHDUxVRNSwXHfkyJGOuBMYVUN+EZRNIwErELCtiECiH1z4EXyGpi8BZJREPyHPga4G3wfj5c7/wbXeq1ev1r5NrnW20v/I34HltEhshgypSLXuzrZu3ar6Cf3lC0PocuQKMQRnoUKFOBLqC7AsI6gEbCsi8HSAH7MRPz+ovcCDh0pg6tSpqp9cI0GGuoMJvpg5c6ZqExz8aIEncOHCBTU6MHr0aDXF0LVrV2nbtq1aWYH8GAizjj6CMy+uEb4eNUD24M8++8yRUh25PkaMGBF4EDwiCfiAgG1FBOY5cYGg6U0AuRDQT/CAt4rhhoE2MWeLPj36/PlztboGPjhI9LZ3715p37696ic4YfvDLl++LMjfg/weOB/gbItEY4wL4g/aLNNfBGx7F23WrJkkS5bMX1xZro8IdOrUSaJHj+6j0vQohgJWj34IrxZwhAzUgwYch4sWLaqOh2NiWSnSkNNIQHcCthURFStWDDWIjO6dZqf6wQkNQcGsZIiASAGrf48iqmWgBSz8MBo2bOgQE8gu6slyVP1psoZWJWBbEYG0v6VKlbJqv1qmXaVLl5YPPvjAMu1BQyhgzdGdiJIaLAF75swZ6d27t1oaipGJ119/XflowBGURgI6EbCtiHjnnXdCrO3XqVNYl/8RQIpm3HStZAUKFKCANUGHYkoh2AL28ePHgiyuOGcgJvBC4q8dO3aYgCCraAcCthURCRMmVN7YduhkM7cR8RbgyW4lgyOdc3AqK7XNSm1BFFKdBOyaNWukZs2aDjGBnB5IWU4jgWASsKWIQHZEKPoxY8YEkz2P7QEBhB12F/XRg1213QRJuZC4iaY3gVSpUmkpYI8cOSJIZZ44cWJ1HcM7Eordvn1bb6CsnSUJ2FJEGFkX582bZ8lOtUqjkA0RYg/DuVaxf/75hwLWBJ2JJcVwqtRZwCLhGx6EkBHWmOqoUaOG1oHZTND1rKKXBGwpIhA7Hz86LqHy8mwJ8ObHjx9X/bRkyZIAH9l/h0MMApx7iF5I05fA2bNnVT+ZRcAuXbpUTb0YYgK+RAsWLNAXMGtmGQK2FBGIm48f2y+//GKZjrRiQ7Zs2aL6afv27ZZpntGmbdu2WaZNVmyI8aCxYsUKUzVv//79KvompgFxjUMq86+//lqePHliqnawsuYhYEsRgbj5+IEhOh1NXwKYbkI/4endKoa8DWgT0lHT9CWAlN7oJyRLM6MhA+nQoUMFcSbQDrzgzGul35IZ+8WKdbaliDDSNDPssN6nNHIb4OJ3/fp1vSvqRe3GjRun2nT16lUv9uKmgSaAVQ8495C23ewGMf7pp5+q9qBNiJGDxHY0EvAFAVuKCCTbiRcvni/4sQw/EoDHOS56L1++9ONRAls0HPXQphcvXgT2wDyaVwSGDRum+unu3bte7afzxogtgWipSEeOcxDLp5GIkEYCkSFgSxGBtdYINkXTm0CLFi3UMja9a+ld7dq0aUMB6x2yoGzdrVs3daMNysH9fFCsToOYTZcunWrja6+9Jq1atbLEqIuf0bF4NwRsKSKKFSsmhQoVcoODH+lEoHLlypI9e3adqhTpumAJHoJN0fQm0LhxY8sJWFfiyFw6bdo0dS3EyAReJUqUkI0bN7puyv9JIFQCthQR7733nor8FioVfqEFgY8//ljN5WpRGR9VApkaKWB9BNOPxSC0tNUEbFi4sNy9bt26SkhATGCkFg7oNBIIj4AtRQSWPXXo0CE8Nvw+yAQyZ84syOJpJcONCaMRNL0JfPjhh+qpXO9a+r52iM2CVPXJkydXgiJOnDjSuXNnoSOw71lbpURbigjMAQ4ePNgqfWjZdiCcb/fu3S3VvhQpUkj79u0t1SYrNiZDhgyWE7De9NO9e/dUCnIErTKmOipUqCC7du3yphhuawMCthMRN27cUD+KKVOm2KB7zdvEp0+fqn7CMk+r2LNnzyRatGgUsCbo0Pjx4wucK2miloNWqVLFISayZcsmM2bMIBoSUARsJyKOHj2qfgzLly/nKaAxAQQCwxPQ7NmzNa6ld1W7fPmyahMzL3rHLdBb37x5U/WTlQSsLxj++uuvaho4QYIEig8SyfXu3Vvu3Lnji+JZhkkJ2E5EbNq0Sf0Adu7cadIus0e1Eb4XImLt2rWWafCBAwdUm3788UfLtMmKDUE0UZx78+fPt2LzIt0mjOaOGDFCOZ4aUx21atViGoFIkzVnAbYTEXiyxYl/4sQJc/aYTWqNiHroJ9x4rWIQD2gT8jLQ9CWwefNm1U/Ic0ILmwDCuJcpU0bxwrmdO3duJpcLG5nlvrWdiBg+fLg64TFkSdOXwOTJk1U/ITCOVWzq1KmqTWfOnLFKkyzZDoxA4IZ4+PBhS7bPH436+eefpWXLlhIjRgzFLlmyZDJo0CCBHxDN2gRsJyK6dOminNus3a3mb92AAQPUxej+/fvmb8y/LcCKINycbt++bZk2WbEhY8eOVf30559/WrF5fm0TfJmQNRQB1XCu44XAXRz59Sv2oBZuOxGBTHapU6cOKnQePHwCWAaJNepWMqy3jxIlipWaZMm29O3bV938mD47ct07c+ZMQXA1Q0wgeByyo9KsRcB2IqJs2bKCtc80vQnUrl1bsFbfSobAWalSpbJSkyzZltatW0vs2LEt2bZgNAq+JQ0bNnSIiTRp0ghXvgSjJ/xzTNuJiHz58glC2tL0JoAY/gULFtS7kl7WDg5ocDyj6U2gevXqlhOwOhA/ffq0WhKKkWCMTmBUDgnpLly4oEP1WIcIErCdiEifPr0gOyRNbwI5cuSQatWq6V1JL2uHEbBy5cp5uRc3DzSBIkWKyEcffRTow9rmeI8ePZLvvvtO8ufP7xid+PTTTwWrYmjmI2A7EREvXjzp06eP+XrKZjXG00q7du0s1WqkXm7WrJml2mTFxiAiY9WqVa3YNO3atHr1apVLxvCbwEMeBAbNPARsJSIeP36slO+YMWPM00M2rSmWisHL20oWN25cClgTdCiWJ7Zt29YENbVOFbGcFo7HyJcDQREzZkzBSrrr169bp5EWbYmtRARiDuAEnTt3rkW70xrNunXrluqnSZMmWaNBInL37l3VJiwfpOlLAHENokaNajkBqy/xkDXDb/+bb76RnDlzqt8LrteVKlUSxKGg6UnAViICkQJxUm7YsEHP3mCtFAGkI0Y/LVmyxDJE4FSGNjGUst5deuXKFdVP06ZN07uiNqgdfv/IHIrfDV6YZpo1a5YNWm6uJtpKRCDpFk7GX375xVy9ZLPabt26VfXTtm3bLNPyHTt2qDZt3LjRMm2yYkMOHjyo+mnFihVWbJ4p27Rv3z61igNxY3D9fv311wWxPJCunBZ8ArYSERMnTlQn4cWLF4NPnjUIlYARdvjYsWOhbmO2LxYvXqzOPWRCpOlLAI5+uFHt2rVL30ratGZ//fWXDBkyRDJnzqz6CP2EeDK//fabTYno0WxbiYgvv/xSnXwPHz7Ugz5r4ZbAqFGjVD9du3bN7fdm/NAIpYx04DR9CWAaAzenkydP6ltJ1kz5tSGWDPoKLyyfhlCnBZ6ArUTEZ599JgkTJgw8ZR7RKwLdunVTF4aXL196tZ/OG3/xxReqTVgjT9OXgJHfhAn69O0j55pt375dmjRpopxhISYSJUok6MMXL144b8a//UjAViICa7+zZs3qR5ws2hcEcFFImTKlL4rSpgwEOHvjjTe0qQ8r4p5Ap06dlNhz/y0/1ZXA+fPnBSPNb731luo/CIqmTZtyRCkAHWYrEVG4cGEpVqxYALDyEJEhgLDkuXLlikwR2u1bpUoVyZIli3b1YoVCEqhfv74kT5485If8zzQEsER36tSpgmRfxlQHrvvwdaH5h4CtRMS7774r9erV8w9JluozAh9++KEgUZqVDBc1ZDSk6U2gdOnSKkaB3rVk7TwhsH79eqlTp45DTGB008yBBrG68JNPPgnxQqbUYJutRESSJEkEw5U0vQlkzJhRDUXqXUvvagePclzQaHoTyJMnj0BI0KxDAKu8unfvLohEaoxOICLppUuXTNXIjh07qumar776SvBq1KiRag+CcwXTbCUicALB6YamN4H48eNLr1699K6kl7VDOF8KWC+hBWFzzKnDJ4dmPQKIGjtu3DiBUDTERKlSpQSpys1gSAwH4eBsiOaJz4NpthER8LbGiTNlypRg8uaxwyGAOU30E5Z5WsnQpkGDBlmpSZZsCwIaWU3AWrKjItkoBBOrXLmyQ0xg9HPy5MmRLNW/u+Ma4jrqYIxO+PfIYZduGxFx9OhRdcIsW7YsbCL8NqgEMMSIH8vs2bODWg9fHhzxLtAm3S9SvmyzGctCBER3F2oztoV19owAohe3b99eMPqJvo8WLZpgifmNGzc8KyBAWyGgFurnGlgrR44cKrdIgKrh9jC2ERGbNm1SnbBz5063IPihHgT279+v+mnt2rV6VMgHtUCGQlwAli5d6oPSWIS/CJw5c0b105w5c/x1CJarKQFkCx0+fLjKz4HfKl4YqUC+JR0MIxCok2H//e9/5fPPP1ef/fTTT8bHQXn/X62CcvjAHRQXBnTCiRMnAndQHslrAqtWrVL9dODAAa/31XUHJHzDuYfAODR9CeABA/20bt06fSvJmvmdwIIFC5RzLc4FvLJnzy7BFpbwhUCcGazOSJcunaoX/HewYiPYZhsRMWLECAWekeiCfcqFfXz4rOCHi7TtVjFkHkSbrJQLxCp949yOH374QfWTlQSsc/v4t3cEkD8FQeJixIihzovYsWOrgFYPHjzwriAfbI1pCzhQYkQCIw+u0xo+OESoRfz+++9KRIXmGG4bEdG5c2eJFStWqKD4hR4E+vfvr36wVsrQN2zYMNUmDJnS9CUAz32rCVh9aZunZkjYOGDAAIHzJc4PvOrWrSuHDh0KWCNwzECNOkBE42GudevWkj9/foeIihcvntv22kZEoNMxDETTmwBO3AQJEuhdSS9rBwWPpxkr5QLxEoEpNu/du7e6QVhJwJoCvEkqid/vjBkz1JSCISY++OADWbJkiV9bgJEHHM8fo7NIRolpvG+//VYaN24sGPEw2obIrUgVMXr0aEE69tDMNiKiZMmSUqBAgdA48HNNCFSvXl2l+tWkOj6pBoJMvfnmmz4pi4X4jwCGrl9//XX/HYAlW4bA5s2bpUGDBo4bLhI7Dh061C8PCggs5asHK6w62bhxo2B0tFatWpIpUyZHGzJkyCANGzZUq8gwheGp2UZEIBcD8hfQ9CZghHXVu5be1Q4pixHKm6Y3AXjj46JKIwFPCZw6dUqQoTdVqlSOm3GzZs3k9OnTnhYR7nYIKIVXROzy5cuycuVK6devnyoDDzPGSMP777+vpizmzp0rFy5ciEjxah/biIg0adIIUoHT9CaQLVs2y4WH1mEtt969rkftkN8EyZpoJOAtAUwLfPfdd+phwbhJwxEy0EvVIV4WLVokPXr0EIy+J02a1CEaMBLftWtX5VvhyzgYthERcKrEnCdNbwKIb48obFay1KlTS/Pmza3UJEu2BflNMMRLI4HIEEDGUEzLGmICv3/4HPjDEIMGSbhwzSxUqJDA+RHHxUoSjIBiKgQxkiBy/GW2EBGPHz9WYM2cwc1fJ4Bu5UaNGlW+/vpr3aoVqfrAqbJnz56RKoM7+58A8psgeiGNBHxBAKs34FSdKFEih6DA+YUphojY06dPlYMjRjxatmwp+fLlk9dee02VjeSSmPJAKIPdu3dHpPgI72MLEYH5HqgzzP3Q9CWAKGzoJ/xIrGKGgB05cqRVmmTZduDcw1I+Ggn4ksA///yjVjg4r3woU6aMivcAoVGuXDlBzhas9HCOanvnzh3Ztm2big0BJ04EvcI5ihcCTdWrV08mTpwoGI0IptlCRCB0KcAjvzxNXwLHjx9X/eTvJVOBJGAIWAw50vQlgDliXCNwUaaRgL8IIKBZ+fLl1bmG8y169OiOv/E/XpiaqFGjRoi4FFmzZlWjDwhcd/bsWX9VL0Ll2kJEIEgHOgfJVmj6Eti6davqJ6hvq9jevXtVmzBPStOXgJGgb/HixfpWkjWzDAFcFypWrKiuDYZ4cH7HqASmQvBAdfXqVa3bbQsRgeFxdBAij9H0JTB//nzVT1YKD42Uwzj3cNGg6UvASNAHIUsjAX8QePTokXJyxHLLTz/9VGLGjOlWRGDaAtcNs5gtRAQ8VHEh96eHqlk6XOd6IjIa+gmps61ikyZNUm06d+6cVZpkyXYYCfqOHDliyfaxUYEngCkyiAGkFsfySlzb8EqRIoXAJwLxJRDgyfgc71GiRHH8nzdvXkEodt0jqNpCRMCTFSE8aXoTwI8Nc4QvXrzQu6Je1A5PHbg4wEmKpi8BI0HfX3/9pW8lWTOtCcD/ad68eSqAEwI5GeIAQqFatWoycOBAWbNmjTifY5cuXZImTZoo/4cKFSooR0o8cCCmkbE/7l3du3cX+IzpaLYQEZh7gmcsTW8C8EC2WnjoVq1aCZZf0fQm0KVLF4kWLZo8e/ZM74qydtoQwLTr5MmTVaho5+RcCJhXv359GTVqlGB67Pbt2xGuM8Stc8AohNDfsGFDhMvzx462EBEYSipdurQ/+LFMHxJAH8GhyEqGUMrvvfeelZpkybZguRyi2tJIIDQCSEKFKVeMKmB0wBgpQLwGjHbD9w6+T0+ePAmtiAh/jmmRjz76yHFMRFedNm2aFqLXFiLinXfeUclSItyD3DEgBPLkyRPhGPEBqWAEDoJUusWKFYvAntwlkAQQ3Q9z0DQSAAEIAYwiIPBdqVKlHJEgkaANodGxDBPLtgMdowGjH0iSZQgYxIuAz9/58+eD1nG2EBFvvPGGWi4TNMo8sEcE8IOwWnhoDHMylLJH3R/UjXLmzKnW7we1Ejx40AjcunVLfvzxR5VzAk/5mNrCjRph+DFC2qtXL8Hy3zNnzgStjs4HhsiBwIGoQT0R6bdp06ayfft2580C8rctRAQgDxo0KCBAeZCIE0DUNvxYrWTx48eXtm3bWqlJlmwL8hs0btzYkm1jo14lgNDTCxYskHbt2gkyPBtP9unSpVPZnhG5FKLiypUrr+6s2ScLFy4M0QYsHw1kdGbLi4ibN2+qE2TKlCmadT2r40wADm34IcMZyUqGNmG4kaY3AazZx+ogmjUJnDhxQvkQYCUEprcN0fDuu++q8NEIS79lyxbBiIRZ7eDBg1KzZk1H27JkySJDhgwJsRrEH22zvIj4/fffFdRly5b5gx/L9BEBPBngh42wrlYxIxcI1nrT9CWAxEY494YNG6ZvJVkzrwjghorMmQgfnSpVKseNFX5XmDKdMGGCSlSFAFBWMywnRwwKIzlX3LhxpU2bNip5lz/aankRYUSi27Fjhz/4sUwfEdi/f7/6oa9du9ZHJQa/GDz94OaEYVOavgSwVh/9NH36dH0ryZqFSuD58+fKF2Dw4MFStmxZgQ8c+hM3Ufg3IHPmjBkzBMmu7GZoN0ZbwAMvxKLwdW4iy4sIIxIdLug0fQmsWrVKneQQEzob8rAggBReSC3/xx9/hFrdn376SbUJQpamLwFDwK5cuVLfSrJmDgJ40sbDBp62ixQp4ggfjZTbJUuWVM6R8BM4deqUYx+7/7Fr1y4lIAwxAUfib775RjBaGlmzvIgwItEhBClNXwLwWcEJHtZNOZi1h6KH01WCBAnUhQsXL6wmwXtohhEItMmOT0ChMdHxc0PA/vzzzzpWz/Z1QoRHrIzAskoswzVuhAhMV6lSJSXo0YeYEqWFTQDJvDp37uxgmDhxYvV/ZMK9W15EIBIdlsHQ9CYAb2hcHHSMEw8Bgbo1atToFeUeluiB0sd+ZvDw1vvs8G/tDAHLJ1f/cva09NOnT6vpB/guwDnQEA34GxEbhw8frhJZwWmeFnECCI6FByODL/xHEJbbW7O8iKhbt67yxvUWDLcPLIHWrVtrGR4aw32YY8VTkLfWo0cPwbLVx48fe7srtw8gAUPAmtkzP4C4fH6o3377TcaPHy+1a9dWYe+NmxqWXiL2ARyTMUrEBIo+R68KxHQrloUa3BEgD4kDPXU6tbyIQLRARBij6U2gSpUqWoaHhnjAFEZE5g4xcpE+fXq9wbN2ynMd8+m0wBDA/PzQoUPVHL1zXoiCBQuquA1wcP31118DUxkexUEACcSwisMQE4id0rt3b8HIUFhmeRGBvAVVq1YNiwG/04AALiBQw7oZ/B4iMgqBdiBcLuLq0/QmgOtD1qxZ9a6kSWt3//59Wb9+vfTt21eFf48XL566ScWOHVsQahyxOebPny90fNeng1++fKlyhCBluSEoEGobcTTcmeVFBEAgrSpNbwKZM2cWTD3pZBhmxY8IKzIiYsgciyVnNL0JILFRWA6yetder9rBcW/p0qXKWQ/J9Izw0UhYhWzKCLyGZFIXL17Uq+KsjVsCiNqJZbKGmHC3keVFBNYKY0iGpjcBDCd36NBBq0oaSzTxHhHDUC3i7mN1xrlz5+T69esezzNG5HjcJ2IE3n77bZWZMWJ723svnNezZ89WWSyRAtu42SAqJHLGYNoCqatx7tPMSwAjRYj26c4sLSLg0IaTGl7yNL0JoJ+QUEYni6yIiBIlivLHgZMSlhp/+eWXKhEcxBKELS6wiJwHL2kGQwtez8PnhaOVnvHHUsCJEyeqUNEZMmRwiAbEHcBNZuzYsbJz507BNAbNHgQsLSLgKIKbUyCTkdjjtPFtK43w0LiZ6mRGvbDE01vDvCLOvZ49e76yKzLwYXkalofioozh306dOr2yHT8IDAH0U58+fQJzMJMdZffu3UoAV65cWVKmTOkQDQUKFFBOeFOnThWEmH7x4oXJWsbq+oqApUXE3r171UkPxx6avgSM8NC+DsfqixZjrhxLPOEf4Y0hQA5uTojfH54ZT3fhbcfvfU/g7t27qp8QfTQ0g3Mt+tJ44akbEUutZljSh+V+aBucnI3w0Wg3Vrl17dpV5s2bJ8ePH7da09meSBCwtIiAQxx+AL/88kskEHFXfxPYunWr6qdt27b5+1Bel4/RAjhI4oL6ySefCJ7I8B6eIx6WqOHcVCP+ngAAHJtJREFUwyhDeIY18AjPTgs8ASxfQz+FNlppjEZhShTTW3hh6S72MXvqcETxhZMjVkhgZAGZTNEuBOcrX768WlGBxIVhBVQLfI/xiLoRsLSIwPA4fhT0BNbttAtZHyzxQj8h46qOhhsJpjTgWW68whuZgHhAmzA/HJ6tW7dOXczD247f+54AfFHQT6GNVhp+Ma43UpwH2C+888D3NY54iZjexUgCArtBGKP+eCEeAKIVIm00OFy7di3iB+GetiNgaRGBHzqWGD148MB2HWumBo8ePVpdzKx08TLa5Mn6d+QFCG0Ntpn60Yx1BXvcSDGv785wDcF0hqsZIxT4Xlc7duyYTJ48WbDGP1OmTA7RgJgYGE3BFM727dsFUzo0EogoAUuLCHhcp0mTJqJsuF+ACHTv3l2Fh7aSc5aR5MaTxG+I0Kd79tIAnQoBPwxWE0BE4CndnWHaCkme3Bn200lE7Nu3TwUJqlatmqRNm9YhGj788ENp1aqVIEfIgQMHBKmzaSTgKwKWFhEIbpInTx5fsWI5fiLQoEEDyZgxo59KD3yxWN6GJZ0QEp4Yngg9GbHwpCxu8/8EkPQMKaOxSiYsQzrpWLFihTpaieWfoQmFYIoIrPCBLxGWRSMyapIkSRyioWjRourcg5+NrlOEYfUJvzMXAUuLCERMQ7Afmt4E4AmOsNdWMHi3I3AWbjB45c6dW/7+++8wm4YbATN9honI6y8RiwMOg5j/x0gXGEOsYdQHUxjwQ0EOBzjKhjZaCT8I9CH8IlzN+C4iy39dy/LkfyQHQ/RAJHVDBMG4ceOquiGYHqKiIu4IVjedP3/ek+K4DQn4jIClRQTSnNavX99nsFiQfwjAyQsXcysYcmUYAsJ4b9u2bZhNw00OT8003xDASBCWI8IwEgG2EGkY7cG0EfxPsCoBT+q4RiBokjszVne5+85I8+7qcOlu24h8dvnyZVmwYIFKSIXR1KhRo6rzCgK1evXqMmjQIFm7dm24AjUix+Y+JOANAUuLCCR7YRAfb06H4GybKlUqad68eXAO7sOj3rt37xUBASGB+WlkKUWKXcyvw1cHT8YzZ85Ujm1wfMPwNM03BDDy079/f48KQ5bVvHnzut0WidcgcF0NTpVY8gvnRF8ZBM60adNU1Ec4PhoCFCIH031w1MWICMWmr4izHF8RsLSIwA8Rip2mN4EYMWK4jeyod63d1875BmDcCCAcmjVrplIfYz1+lixZVPQ/Y0ja2A7vSFSEYEaYhkMY4V69eqlQwhiCx3LEU6dOyT///OP+4PxUEUDsB9x0PTGIAfgUuDM4VboKBYw8oH8imh7eOA5WgyAQGZZWQsgY58D777+vRCZCpcNR8unTp8YufCcBLQlYVkQgrDB+mFjiRNOXwLNnz1Q/jRo1St9KelEzI+aFcVNAFtmwnNuwegMRALHUDnPayEuAp+h27dqpBEaIFIh09ijHyIholI2gQEh0VLhwYalZs6ZKWY61/hjhwHp/3Kiw6sBueQzQboRj9sQwTYAnfXcGzp9//rkgCBqiOCK4FD7D6IQ30xhYDYH+HTx4sPJfcE6xDP8GHGPWrFkqBLq7evAzEtCZgGVFBC7c+MEj4hpNXwKY+0U/4SJqFcPQNObMsaQOQ9++Mqznx0gERiQQzApPq5gWgRNhnTp1pESJEuoGh+mh6NGjK65gixcECIIKYege0QhbtGihIhJCtPzwww9qqPzo0aNqjh3CzsyGYf+FCxd61ASwgQOmq0EkYCTC+YVRCU/SwmPKAf4KWPmB6KYYtTD6oUyZMupzMD979qzrYfk/CZiOgGVFxObNm9UPl9kR9T4nsW4dF1hcdGm+I4BhcERqRf4YOBFC0GBqD0+99erVk5IlS0quXLmUsMB0knGTM94TJkwomJrBSAi279KliwwfPly+//57WbVqlSAxE6YNsGpAN0P91qxZE261ENwM7Y1sll/kScF0E3woEJPB4Imlo1WrVlVCb/Xq1fLnn3+GWyduQAJmI2BZEQHPa1wguP5e71MSy9bQTwy2FNx+wg310KFDaukjli1iWgRxLjDUD58BLFWFgyhujIbQMN6RcwEOgHAchQMpAhv17dtXzfkjzPKGDRtU/hqImocPH/q9oTimJw8Phw8fVm2BAPDGIJ7ACM7A8GEwOCRLlkytBsPUHGI4+HIUypv6cVsSCCQBy4oIBPvBj9uTiIGBBM5jhSSAJ2T0E9e3h+Si838Yrj958qSaAoEPCJwYMSWAVSYYrseUCUJFx4kTx3GDNW60eMfNFjdfiBOMcuAJfuDAgWp6Bn4h8EHAdOTVq1cjlGIa0zye5LSAGMA0kLs4EM78Udb48eOldu3aygfFaMvbb7+tpoUwJbRnzx55/Pix8278mwRsQcCyIgLDr1hTTdObwIABAyRKlCiC5ZE06xHAjRXOnbjJwj9pwoQJapQCT/HlypUTBITD6gQsxzZuzs7v+Bw3648++kgQgbZp06Yq4BIeEjAagJEslH3mzBm5ffu2AojvwvM3wMoX4ziFChVS+xv0EYRq6NCh6ngIRGVsh9EYCB44rmIUg0YCJCBiWRGBJ5x3332Xfaw5gTZt2qjljppXk9ULEAHEeMCTP3xkEF0SIxRYqYJ8EBASCI8eP358x43duMHjHWI0ZcqU6uEhc+bMAnGA6RXE5UDoaqzUgm8CVkk474e/US4ipyZOnNjxHcJH9+zZUxYtWqT8PwKEgIchAVMRsKyIgEMYlr7R9CaAizwc/Ggk4C0B+BxgeSz8D+AHMXLkSOUAihgbOKcwiuAaiwPRH53DkjuLCYyMYHktRjcYhtzb3uD2diVgWREBz3J4RtP0JoDgS3gCpJGAPwicO3dOZs+erYJ9Zc+eXY1WOAsH428EnaKRAAl4T8CyIgJZ7Vq2bOk9Ee4RUALIW1C3bt2AHpMHsy6BI0eOqIBdmM50jh6KGBmIGgoHSUSKNMSD8Q7fHBoJkID3BCwrInBxQGY7mt4EML+NYEk0EogIAcSrgCMlRh2dw0fDH6p9+/YqroW7lRo7d+5UvhJYnTF37tyIHJr7kAAJiEUdK5HMCCIiskFkeIb4nwD6iU+B/udshSM8evRIkGodIaixlNQ5fDSCPCEbKjJfIqonjQRIIDAELDkSgSVluDkh4BRNXwJwjEM/fffdd/pWkjULGgHEeEG0TcSgcA0fDT8aiImVK1fKpUuXglZHHpgE7E7AkiICoX5xc0ISIpq+BBBNFP2EPAI0EoD4xyqL1q1bhwgfjbwfWOI5bNgw2bhxoyC5Ho0ESEAPApYUEXh6wc0J2fxo+hJApED0EyIU0uxH4NixYyp2AxJbOYePRt4OBIMaN26cIPDTgwcP7AeHLSYBkxCwpIhA2FvcnBCrn6YvAcxfo5/CSpWtb+1ZM28J7Nu3T4XIRtpypDBH3+OFENlt27aVadOmqRwbL1++9LZobk8CJBAkApYUEYhOh0RBfIIJ0lnl4WGRcwE3EeRIoFmLAJybEQQKqcorVKigAj8ZouG9995Tfg7Iu8EEedbqd7bGfgQsKSIQ5hZPNzS9CcCbHkF+Xrx4oXdFWbtwCSAlOCI99ujRQ0qUKBEifHTBggXlyy+/lOXLl6s8GuEWxg1IgARMQ8CSIqJSpUqC8LY0vQkg6yNyHNDMR+Dy5ctqOSXyWkAkOGfsLFu2rEpghRTg169fN1/jWGMSIAGPCWgvIuB8h6Vcrq+w0vciMyDi59P0JoBlergB0fQngGkH+Cwg6iOyWSLZFaYnYsaMqVJkIwrkjh07mI1V/65kDUnApwS0FxEYVcDURJEiRUK83EWhM8i8+eabUr9+feNfvmtKAHPj6F+afgSwsgnCACHJEf3R8GdIliyZCic/depUtfqJU1H69R1rRAKBJKC9iICAgKOkN4ano88//9ybXbhtEAjghtS8efMgHJmHdCbw/Plz2b59u0qRjayq6dKlc4iGt99+W2XGRGhoLMmkkQAJkIAzAa1FxB9//KEuZmFNXTg3xvgbT02DBg0y/uW7pgQwJN6zZ09Na2fdat25c0fWrl0rX3zxhZr2S548uUM0YKqiT58+smzZMsHvj0YCJEACYRHQWkTAmxuCAOGRPbV//vlH7TN58mRPd+F2QSCAp1/07ciRI4NwdHsd8q+//pLFixdLp06d1JQgkp4Z0xMIJz148GBZt24dl9ra67Rga0nAJwS0FhGYxvB2qSYCF+ECiScpmr4E4N2Pfpo1a5a+lTRpzU6fPi0zZsyQVq1aCZyMo0eP7hANFStWVInpMH1x9+5dk7aQ1SYBEtCFgNYiAs6UiCOApyXjFZ4j3ubNm9UFE57iNH0JHDhwQPXTmjVr9K2kSWoGJ+Px48cLwkfDWdUYZYgXL55yMMao3P79++XZs2cmaRGrSQIkYBYCWosIXAwhGjAiYbzwhBWWISMk9hs7dqxKG4xkXHAIQ6Y/TItgGJ0WfAIITIR+ws2N5h0B5JMYOnSoIHw0HB8N0ZAqVSpp06aNzJ49W44ePepdodyaBEiABCJAQFsRgacrXBy9daqEsxj2Q2bIpUuXysyZM1UiH8z79urVS8Xo79q1q/Tv31/9j/liWuAJYIkg+un8+fOBP7iJjnj//n2VjRYRHxE+OnXq1A7RkCVLFuWYumTJEjl37pyJWsWqkgAJWIWAtiICIw64yXhriIKIYdywDBdmiAeMbhw5ciSsTfmdnwgMGDBAYsSIEeq8PEaNkN3TnVMtVg2EFSfET1UOSLHIIwLx261bNxU+OlGiRA7RAP+GgQMHCqaAKH4D0h08CAmQQDgEvL9Lh1Ogr77u2LGj5MiRw+viSpYsKRjW9cQwJMxlbJ6Q8v02GHZPkyZNqAWHJSIx9w9/GSsYRhAw/WCEj44dO7ZDNCAHBZKUYTTu9u3bVmgu20ACJGAxAtqKCAgICAlvLWfOnJI1a1aPduvdu7fcvHnTo225kW8JVK1aVXLlyhVqoej70IQCzg2MIpnRMPI1ceJER/hojLbhFTVqVKlWrZrApwd+PMiCSSMBEiAB3QloKyJwk/DWHwKw8XRbqFAhj7h36NCBF2uPSPl+o48++kiQOyM0g4BwJyIxvYGbLmKImMF2794tI0aMeCV8NFYdNWnSRC1x5ZSaGXqSdSQBEnBHQFsR4a6ynnwWN25cQeje8OzRo0cq+E542/F7/xBInz691KlTJ9TCIRTcrcSBsMR3Ok5D4ZzatGmTwN/DNXw08rlAFCHo05kzZ0JtN78gARIgATMRsJyIwJI3BNkJz5CiGB7vtOAQwNw/RoLcmSEUxowZo5wr4WBpvBo3bux1ADJ3x/DFZzdu3JAVK1aoVT7IGuscPhrxGvr27SurV6+WP//80xeHYxkkQAIkoB0BS4kILOfEVMb06dPDBQ2HNgwz03xLAKsmzp49K9euXZOHDx+GWjhGE/DE7s6++eYbh3MhtnN9hRdwzF2ZvvjswoULMm/ePJXcDdMtzuGjkdIc59OWLVvk1q1bvjgcyyABEiAB7QlYRkQUK1YsxM2madOmYcLHzW7SpElhbsMvvSOwfv16ad26tbqZYpQHuRow2gAHVqyEmTBhglqJgBsxhAGcCN1ZWKsvEiRIEDCnSgQpQ7THzz777JXw0WXKlFEOknv27JHHjx+7awY/IwESIAHLE7CEiJg/f34IAWE8uf7666+hdiDCYuNmRvMdAQT4wpO4sz19+lSQFA1P8XAg/Pnnn8UINIV+c2ehpX+HHwT6NiIOt+6O4/rZvn37VF4JxBpxDh+N1PK1atVSPhqHDh1y3Y3/kwAJkIBtCVhCRPTr18+tiEBYYNx0MOycLl06yZMnj5QtW1YwSlG3bl3p0aOHIIQwht+ZjCjyv4Hvv//eozDWGzduDFUMhLX6wsjqGvmailqVs3XrVpXBskaNGiHCRydNmlRatGghCxcuFCSzopEACZAACbgnYAkRgWF0Y/TB+f3gwYPSvHlzQebCAgUKSObMmZXzm3NAH+ftDcGB7TDnXbt2bTX/PWzYMLUUDze/w4cPK0c5ruN/9YT69ttv5cSJE69+4fLJlClTVH8h46qrGU6V7lZfYNlvRAKQ4RjwU0C+Djg7li9fPkT46IwZM0qXLl1k1apVguyiNBIgARIgAc8IWEJEoKmYe3cWBCNHjgyVALIZXrlyRTA0jSV5CxYsUAm7MI+POX08mSJraPbs2ZXoQCAg57KNv1977TVJmzat5MuXTwmVli1bqvl6zPXDax+jHCdPnrRNQKuvv/5acQ0V/L9f9OnTR/FEiGdXg1AILf07hB38JTwxiAH0K/KkFC9eXJzDRyPIFXKnoO8x1UIjARIgARKIGAHLiAg0/9SpU+pp09d5BTDVgWFtiAIMqWNOHwm9OnfuLA0aNBA42eXNm1fd/BCnwhAZru+JEyeWbNmyqZwI9evXV/kRRo0apZwN161bJ0iPjSfwe/fuRaw3g7xX9+7d5c6dO+HWAkGWwMldRlWICHdBplAoRIS72BH4DiMg06ZNUwnWEMjKebQJ+2G5KPwxwloxEm7FuQEJkAAJkEAIApYSESFaFsR/EIMCToSY/pgzZ45y1kN2UYxUIAjRxx9/LMjACFHhKjSM/3ETREAm3BARIrpt27bq6RkrHBCwCPP5OAYEE5wXdTCM4rx8+TLcqiCmQooUKcLdLqwNMFU1btw45d+CkQWDG96R7RLLfMNyrA2rbH5HAiRAAiTgGQGKCM84+W0r+FZcvHhRsDIAc/LwF8C0AKZnENERoaGRDwThvLFKwPlm6fw3Ah1hO9ygEZAJw/hYVomb6cqVK9VTOEZq/DV8j9EajER4Yrlz55Z3333Xk03VNhix2L59uwwfPlwxgQAz2o4RjXr16qmpC0wd0UiABEiABAJHgCIicKx9ciRMF0AM4Ka6aNEigTNjr1691BM5nsDhQIqoncjNYNxoXd9ff/11eeedd6Rw4cIq6RPiICCWA4b8586dK3BUxZM+lmUibbonhqiMED/hGUZOIHAglkIztHHt2rVq5KVy5cpqmshoQ8qUKQUZQOFzAvFFIwESIAESCB4BiojgsQ/IkeG8iBUlGzZsUCtMsNIEQaAwylG0aFEVDwFTC3ASNW7Uzu/RokVTKxkweoA061gai1ESRJuEAyliQ2BFBUZR8BmcVkMzTMU4lw1/EhiEBaZoevbsKaVKlZJkyZI5tsNKGXyOqSGEmaaRAAmQAAnoQ4AiQp++CHpNEHkRow9IRY0nfUT0RAwO5CLBiED+/PmVn0a8ePEcN3lnUYC/48SJo1a04OaPUREsp0RcjuPHj7sVKpiawMiIUc4HH3ygnFZ37tzp8ShI0MGxAiRAAiRgUwIUETbteF80G4Gh4IeA5FgIzIQlss2aNZNy5cqp1SoI8IUw1RAIcBA1hILzO5bIjh8/Xn755RePnDJ9UW+WQQIkQAIk4BsCFBG+4chSnAhgKSySaCF8NGJtOIsG178nTpzotCf/JAESIAESMBMBiggz9ZaGdYXjJRwxETcDQboQ/dEQCnDuxEoRxNbANEm3bt0c32EbjE7QSIAESIAEzEuAIsK8fReUmsNRc9myZY7w0alSpXIIgzfffFM5XUJUIBW4O4ODJAJKzZo1y93X/IwESIAESMBEBCgiTNRZwajquXPnVLZTI3x0woQJHaIBUxUIYY2MqGaNshkMpjwmCZAACViFAEWEVXrSR+1AFEzn8NGxYsVyiAZMPyDgE8JzuwtZ7aMqsBgSIAESIAGTEKCIMElH+auau3fvDjV8NKJfYpnnsWPH/HV4lksCJEACJGBiAhQRJu48b6v+6NEjlbnSXfjoGDFiSM2aNVX46PPnz3tbNLcnARIgARKwIQGKCAt3OiI8IpIk0l67ho9OkiSJNG/eXNasWSN///23hSmwaSRAAiRAAv4iQBHhL7JBKBfLKJFPw1346AwZMkiXLl1UYChP0nUHofo8JAmQAAmQgMkIUESYrMOcqwtfhZkzZ0rHjh1VMi3n8NHI6IkRCGQH1SVVuHPd+TcJkAAJkID5CVBEmKgPIQiQ9Kply5aSL1++ELkoihQpoqJEHj161EQtYlVJgARIgATMTIAiQtPee/LkicqOOXr0aEG2S9fw0Uj7PX36dDl79qymLWC1SIAESIAErE6AIkKTHr5165asXbtWBg0aJNWrVw8RPjpu3LhSr149lXYbabNpJEACJEACJKADAYqIIPXC5cuXZenSpSriI7JeOoePTpkypbRu3Vo2bNggyJRJIwESIAESIAEdCVBEBKhXTpw4IXPnzlUrJIoVKybO4aMzZ84sPXr0kD179gimMWgkQAIkQAIkYAYCFBF+6qVffvlFpk6dKm3atJECBQqIc/hoOEVi2uLw4cN+OjqLJQESIAESIAH/E6CI8AFj5JHYtWuXjB07Vpo0aSJYXmmkw8Z78eLFVWjpM2fO+OBoLIIESIAESIAE9CBAERGBfkCwpk2bNsmwYcOkdu3agukIQzREiRJFqlSpolJdX7lyJQKlcxcSIAESIAESMAcBiggP+gkrIhA+ul+/flKpUiV58803HaIhQYIE0qhRI1mxYoVghQWNBEiABEiABOxCgCLCTU+fPn1ahY+Gs2PJkiUladKkDtGQNm1aad++vWzdulWQ0IpGAiRAAiRAAnYlQBEhohwcET66Q4cOUqhQIYkXL55DNGTLlk0twzx48KBdzxG2mwRIgARIgATcErCliNi7d68KH92iRQvJmzevRIsWzSEasJICqbJPnTrlFhg/JAESIAESIAES+H8ClhcR9+/fd4SPrl+/vmBkwXCCxHvp0qVl0qRJcunSJZ4TJEACJEACJEACXhCwnIi4evWqI3x0tWrVBCmwDdEQPXp0qVmzpsyfP19u3rzpBSZuSgIkQAIkQAIk4ErA9CLi/PnzjvDRZcuWFYSMNkRD4sSJpXnz5rJ69Wp58OCBa9v5PwmQAAmQAAmQQCQImE5EHDt2zBE+umjRovLGG284RANGHTp37iw7duyIBBLuSgIkQAIkQAIk4AkB7UUEVkUY4aPz588vMWPGdIgGRIZE7IZDhw550lZuQwIkQAIkQAIk4EMCWokIxF3YuXOnI3x0jhw5HIIBUxSFCxeW0aNHC6YwaCRAAiRAAiRAAsElEFQRcePGDdm4caMjfHSmTJlCiIby5cvLtGnT5Pr168GlxKOTAAmQAAmQAAm8QiCgIgLLKFeuXOk2fHScOHGkbt26snjxYsGyTBoJkAAJkAAJkIDeBPwqIhCwaeHCheIufHSKFCmkVatWsmHDBnnx4oXelFg7EiABEiABEiCBVwj4VETAwXHGjBluw0djqqJ79+6yZ8+eVyrBD0iABEiABEiABMxHIMIi4smTJ0oQTJw4UdyFj0Y46YEDBwqWZNJIgARIgARIgASsR8BjEXH79m2VuXLUqFHiLnx0sWLFZNy4cXL58mXrUWKLSIAESIAESIAEXiHgkYhwDR+N5ZaVK1eWWbNmyZ07d14plB+QAAmQAAmQAAlYn4BHIiJ+/PjSqFEjWb58uTx//tz6VNhCEiABEiABEiCBcAl4JCLCLYUbkAAJkAAJkAAJ2I4ARYTtupwNJgESIAESIAHfEKCI8A1HlkICJEACJEACtiNAEWG7LmeDSYAESIAESMA3BCgifMORpZAACZAACZCA7QhQRNiuy9lgEiABEiABEvANAYoI33BkKSRAAiRAAiRgOwIUEbbrcjaYBEiABEiABHxDgCLCNxxZCgmQAAmQAAnYjgBFhO26nA0mARIgARIgAd8Q+D89kkuFKsT14AAAAABJRU5ErkJggg==[/img][br][br]Why is [math]GHFE[/math] not a dilation of [math]ADCB[/math]?
Sort the cards into categories of your choosing. Be prepared to explain the meaning of your categories.
[size=150]Your teacher will assign you one card.[/size][br]Write the sequence of transformations (translation, rotation, reflection, dilation) to take one figure to the other.[br]
For all the cards that could include a dilation, what scale factor is used to go from Figure [math]F[/math] to Figure [math]G[/math]? [br]
What scale factor is used to go from Figure [math]G[/math] to Figure [math]F[/math]?
Find a sequence of transformations that takes Figure G to Figure F.
How does this sequence compare to the sequence that took Figure [math]F[/math] to Figure [math]G[/math]?
[size=150]Are the triangles [b]similar[/b]?[/size][br][size=100][img]https://i.ibb.co/5Wqyzbw/Geo-3-6-3.png[/img][/size][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAT8AAAD9CAYAAADK8XCgAAAgAElEQVR4Ae2dC7QVVR3GRd5vCCN5yEURCsEuigqmCakkBgFqklJyJTWRhxfLB5LCTS3JpaESIQhyLVAwCNBYhCBcHwkUy4uSi+ViBZQvfPBQzFCD3fr+ua9z5szznDPvb68168yZ2XvP3r//nm/2a/YcpehIgARIIIMEjspgnpllEiABElAUPxYCEiCBTBKg+GXS7Mw0CZAAxY9lgARIIJMEKH6ZNDszTQIkQPFjGSABEsgkAYpfJs3OTJMACVD8WAZIgAQySYDil0mzM9MkQAIUP5YBEiCBTBKg+GXS7Mw0CZAAxY9lgARIIJMEKH6ZNDszTQIkEBvxq6ioUAMHDszb9u/fTyuRAAmQQMkJxEL8IHBHHXWUggBOmzYtZyt5jhkhCZAACSgVj1VdNmzYIOK3a9cuGoUESIAEQiEQi5ofantlZWWeMvzoo4+qYcOGqYsuukgtXrzYUxh6IgESIAEzgViI3/DhwxU2NzdjxgypIaKJrLd58+a5BeN5EiABEsgjEAvxa926teratWvOYEdlZWVeYnv27Fknelr8+vfvn+ePB0iABEjAjUDk4od+PqvBjuXLl+elvX379nni17179zx/PEACJEACbgQiFz+IHMTPy5SW6667Lk/8brnlFrc88jwJkAAJ5BGIXPww2FFeXp6XMKsDhw8fVqNHj84RwL/+9a9WXnmMBEiABBwJRC5+AwYMkPl9jqk0nUQfYdu2bUUE+/btazrLvyRAAiTgTiBy8UOT98orr1Q1NTU5m1PSIX7t2rVTp59+ugjgihUrnLzzHAmQAAnkEYhU/Gpra3OasHoEF7VBJ6fFb8eOHapevXqqR48eTt55jgRIgATyCEQqfnmp8XhAix+8Dxo0SAT0t7/9rcfQ9EYCJEACMXm9za8hjOL38ccfq/r166uOHTv6jYb+SYAEMkwg8TU/2O6yyy6T2l9VVVWGTcmskwAJ+CGQCvFDhps0aSIjwH4yT78kQALZJZAa8Zs4caLU/saNG5ddazLnJEACngmkRvyQY/QFNmvWzHPm6ZEESCC7BFIlfnfeeafU/kaOHJldizLnJEACngikSvyQ4w4dOqgGDRqoffv2eQJATyRAAtkkkDrxw/p+mCyN+X90JEACJGBHIHXih4yeeOKJIoBbt261yzePkwAJZJxAKsVv9erVIn5nnHFGxs3L7JMACdgRSIX4HTlyRD3wwAM5eTz11FNFAFetWpVznH9IgARIAARSIX7ICBY1ff/99+usun79ehE/rP5CRwIkQAJmAqkRv0ceeUQ988wzatOmTWrWrFlq8uTJskgqBj8efvhhc775nwRIIOMEEit+bdq0UZs3b1Zr165VixYtUljiHiO8c+fOVXp15w8//FAWPejcuXPGzczskwAJmAkkVvyaN2+uFixYoJYtW6aee+45tWXLFqntmTP4ve99T5q/mABNRwIkQAKaQGLFz6ov74477lD/+te/dN7qfhs3biwrP9cd4A4JkEDmCaRK/BYvXqzWrVuXZ9SxY8dK7e/666/PO8cDJEAC2SSQKvFzMmGrVq0Umsp0JEACJAACmRG/qVOnSu1v1KhRtDwJkAAJZEf8YOuvfOUrqmHDhurgwYM0PQmQQMYJZKbmBzvPnj1ban+DBw/OuNmZfRIggUyJH8x9wgknyOcuX331VVqfBEggwwQyJ34rV66U2l///v0zbHZmnQRIIHPiB5OXl5eLAK5Zs4YlgARIIKMEMil+tbW1In4nnXRSRs3ObJMACWRS/GD2c845RwSwurqapYAESCCDBDIrflj+6uijj1ZdunTJoNmZZRIggcyKH0w/YsQIqf1Nnz6dJYEESCBjBDItfocPH1aNGjVSxxxzTMbMzuySAAlkWvxg/quuukpqfzfccANLAwmQQIYIZF78YOsWLVrIliG7M6skkHkCFD+l1JQpU6T2N3r06MwXCAIggawQoPh9bukvf/nL0v936NChrNie+SSBTBOg+H1ufnz6Eh87GjJkSKYLBDNPAlkhQPEzWLqsrEwWPdixY4fhKHdJgATSSIDiZ7Dq0qVLpfZ31llnGY5ylwRIII0EKH4mq/bu3VsEcMOGDaYz/EsCJJAmAhQ/kzU3btwo4nfyySebzvAvCZBAmghQ/CysiWYvBj8WLlxocZaHSIAE0kCA4mdhxTfffFMGPo4//niLszxEAiSQBgIUPxsrDh06VGp/9957r40PHiYBEkgyAYqfjfUw2Rlfemvfvr2NDx4mARJIMgGKn4P1KioqpPZ38803O/jiKRIggSQSoPi5WK158+aqZcuWLr54mgRIIGkEKH4uFrvpppuk9jdmzBgXnzxNAiSQJAIUPw/WateunWrcuLE6cuSIB9/0QgIkkAQCFD8PVsKIL+b9DR8+3INveiEBEkgCAYqfRysdd9xx8sGj3bt3ewxBbyRAAnEmQPHzaJ1FixZJ7Q+fvKQjARJIPgGKnw8b9uzZUwTwhRde8BGKXkmABOJIgOLnwyrPPvusiF+fPn18hKJXEiCBOBKg+Pm0Sv/+/UUAlyxZ4jMkvZMACcSJAMXPpzV27twpix5069bNZ0h6J4EvCEybNk1VVVXZbl/45F5QBCh+BZAdPHiw1P7w3Q86EiiEwIABA5TeWrdurfAJBf0fv3TBE6D4FcD4o48+Ug0aNFDHHntsAaEZhARyCWAO6YwZM3IP8l/gBCh+BSL+wQ9+ILU/fPOXjgQKJYDPJUD8amtrHaN46aWX1B133KGmT5+u+IEtR1SeT1L8PKPK99i0aVOFJgsdCRRKADU+iJ+Te/zxx8UP/GFDq6OmpsYpCM95IOBM3UMEUXiB4OB926jdpEmTpDBec801USeF108oASyb5tbHd8opp+SIHwSQr1oWb3CKX5EM27ZtK4seFBkNg2eUQHl5uaqsrHTMPVoYutanf7/61a86huFJdwIUP3dGjj7QB4MCefHFFzv640kSMBPYv3+/lJ3ly5ebT+X8HzJkSJ74XXvttTl++Mc/AYqff2Z5ITp16iSLHuDDR3Qk4JWAHuzYtWuXY5Bt27Yp/T1pPGjr1aunXn/9dccwPOlOgOLnzsjVR3V1tTyZv/Wtb7n6pQcS0AQw0dnPgBmav40aNZKyhrmmdMURoPgVx68uNPpg8FTetGlT3THukIATAQxa+Bm4wCcV0Mro3Lkza39OYD2eo/h5BOXmbe3atSJ+p556qptXnicBIYBaH2p/Xp0Wvz/96U9S1vr16+c1KP1ZEKD4WUAp9NBpp50mhfKPf/xjoVEwXIYIoM8Pgx5enRY/+NfLq23cuNFrcPozEaD4mYAU83f79u0ift27dy8mGoYlAUsCRvHbsmWLlDVOebFE5ekgxc8TJu+eBg0aJIVy1qxZ3gPRJwl4IGAUP3g/88wzpay5TZXxEHUmvVD8Smz2AwcOqPr166uOHTuWOGZGl3UCZvHbs2ePDHywrBVWMih+hXFzDPX9739fnshTp0519MeTJOCHgFn8EFZPgH7ooYf8REW/SimKX0DFoEmTJr7mcAWUDEabIgJW4vef//xHWhpt2rRJUU7DyQrFLyDOEyZMkNrfddddF9AVGG3WCFiJHxiMGTNGytrkyZOzhqSo/FL8isLnHBjzuFADpCOBUhCwE7/Dhw9LOUNZwz6dNwIUP2+cCvKFxSfx1sell15aUHgGIgEjATvxgx/U+lDWUAuk80aA4ueNU8G+sNQ9Rn/fe++9guNgQBIAASfxw/lWrVrJQqfoB6RzJ0Dxc2dUlI+5c+fKE/n8888vKh4GJgE38Zs5c6aUtaFDhxKWBwIUPw+QivVy4oknSqHEdxjoSKBQAmbx+/TTT5X5VUrM+cOSV2+99Vahl8lMOIpfCKbWL6KffvrpIVyNl0grAbP4/fe//1Xjx49Xhw4dqsvyypUr5UGLtz/onAlQ/Jz5lOys/g7DU089VbI4GVG2CJjFD7l/8MEH1SuvvKLeeOMNBeG75ZZb5JOqGPxgS8O5fFD8nPmU7OzWrVvlicwX0UuGNHMRQfw6dOig8Frba6+9pp5//nkZ5cUbRbfffrs0gbGa+ObNm6WsYeUXOnsCFD97NiU/g5We8USeM2dOyeNmhOknAPFr2bKlqqqqko+cL1y4UC1evFjddNNNeZk/44wzpKw9+eSTeed44P8EKH4hlgRMdzn66KO56EGIzNN0KatmL/J38803q7179+Zk9Z///KcMfGDVZzprAhQ/ay6BHb3kkkvkiYwJ0HQk4IeAnfjNnz9fvfjii3lRXXjhhVLWMN2KLp8AxS+fSaBHPvvsM/nOL19EDxRzKiO3E793333XMr960QN8W5ounwDFL59J4EfwzVX0/U2cODHwa/EC6SFgJ35OObziiiukrN12221O3jJ5juIXkdnRcc1FDyKCn9DLFiJ+mAvYuHFjKWtc9CDX8IGLHz7QMmLECLVgwYLcK3/+b8CAAWrgwIF5m6Xnzw9itZR27do5eYn9OUxNQO3v8ssvLzqt+BAORgDNTh/HOasN5+mSQ6AQ8UPubrzxRilrV199dXIyG0JKAxW/2tpahb4tu0/0QRghAJWVlfIJP3zGT29OeU+D+CF/7du3l0UPPvjgA6fsOp6bMWOGMARHs8MDBw8Xqw3+7R5I5nj4Px4EChU/pF4veoBX4uj+TyD/jikRGdxY+gbDzWf1fVLUPKxuWrckpEX8fvOb30j+L7jgArcs553XNeqysjKZ8+WHI2wDhnTJIlCM+D3wwANS1vx8JD1ZdPynNjDxg7Ch5gdH8bM3zPHHHy+Fctu2bfaebM6gxgwR9PsQgWBaPYxsLsPDMSFQjPghC1heDfNM33nnnZjkKNpkBCZ+xmzZiR8+uVdIDSQtNT8wwqocqLX169fPiMzXvh/x0zVyiCZdsggUK35LliyRsnb22WcnK+MBpTZS8UPtA32CuPmxYR+DI7rGaJfnNIkf8lheXi75X716tV2WHY/7ET9cq6KiwjE+nowngWLFD7nq3r27lLWXX345npkMMVWRih/yiRsX265duxRqgqglQgTx386lTfz0i+hf+9rX7LLseNyr+Gl/TmwdL8STJSeAGnhNTY26//775dfpAqUQP7wJgopG7969nS7l+RzK1IoVK2Tz0ppA2UN+EcatkuM5EQV6jFz8zOkGQLc+qbSJHxicc845UigfeeQRMxLX/1rU3DziwcIObzdK4Z1Hny2ECOUdtkGt3MmVQvwQf9++feW6a9ascbqc4zlUVHSrDWnH5iZm6HJBGOQT/nEfY5qbF9F0TEyBJ2MnfsiHhmmXpzSK39tvvy2d0Z06dbLLtu1xL+KHgokbDX7poieArgeInh97lEr8du7cKYsedOnSpSAQurz5GTRDjQ/lD1OztPNS0dF+g/iNpfjhyeAENo3iB+OiVoYC8stf/tKXrXVhdAqEmw0PFbroCegHkVtNyZzSUokf4h00aJCUNSyK4NcV0m9sV0bdKjp+0+bHf6Tih6qzscqL/UmTJkl12KlfKq3i9/HHH6tGjRpJ08CPEe0Klo5DP3XR7KCLngCau25NXKtUllL8Cl30oFDh1mXQXPPr2rVrTm3QKt9BHYtU/FAbQU0HAPr06SP7aApAFJ1cWsUPef7Rj34kHG644QYnBDnn3MRPN7FyAvFPZARQ24EAwm6Y3YB+Lzz0nR74SGwpxQ/x4dVK3H9Wr0bawTFOlUKakXbkwe2eRXw6LMJhwAP3PMpmVC4U8cPTws6wOI5CgM1rMyDN4oeC0KJFC1+LHqDGDH52Dufs+NuF4fHgCED8cOPjF4IA4UCXh9ssh1KLHxY9QEujWbNmnjOL7igIpu6aQtmCkOOedOqq0hfQFR7EAQZRlstQxE9nvFS/aRc/fIQGheOHP/xhqZAxnhgRQPmF8JmdW19aqcUP10ctDGVt7Nix5uRY/tfiZ66oQMQh3k4O+cOmKzpa8M1xOcVRynMUv1LSLGFcxxxzjCx6gH5AunQRgPBZ1ZJwzEoUde6DED/EjeXVGjRooLwseqAX0tBp0r8QMIionZAhHETf2MePsKgJotsrCkfxi4K6h2v++te/lsL0ne98x4NvekkSAdR4rPq60HyMQvx0Wbv44otdMaLWBpEzi5g+bteMRX6t8qbDuV44AA8UvwCglipKDP6goOEzhXTpIYAbHrUgYy0JYuI28hlUzQ9ksbwaFj0wi5oVdZRLc80V/3FcO5TZP/zhD/qv+Ef+zPEjHFhE4Sh+UVD3eM3HH39cxO/MM8/0GILekkIANSH0kelFZtH5j/4wszgY8xOk+D322GNS1qxqZ8Y0YB8DNHgoX3nllZJ+/OK/ccR32LBhcmzTpk0SHPmCyGF0GHmurq6W8AiH/sIoHMUvCuo+rtmrVy8pROvWrfMRil6TQAA3PZrA2NAn5iR8yE+Q4of4TzjhBClrf//7313xodaqm7JorhtrsQiMrxPi28EHDhyoiwv5Qz6RX4gsan3mcHWeQ9ih+IUAuZhLPP/881Ige/bsWUw0DJsCAkGL3/r166Wsff3rX08BLfcsUPzcGUXu4xvf+IYUyt/97neRp4UJiI5A0OKHnJ1yyilS1rLQ0qD4RVeWPV8ZI2j16tVTnTt39hyGHtNHIAzx27Fjh4hfVNNPwrQaxS9M2kVca8iQIVIo77nnniJiYdAkEwhD/MDn3HPPlbK2cOHCJONyTTvFzxVRPDx8+OGHqmHDhqpt27bxSBBTETqBsMQPXxPEtBdMtE+zo/glyLpXXHGFPJHxHVa67BEIS/xAduTIkVLWfvGLX6QWNMUvYabFS+hNmzZNWKqZ3FIQCFP89KIHuGZaHcUvYZb9yU9+Ik9kTCylyxaBMMUPZMePHy9lbcKECakETfFLoFm/9KUvyaIHeDrTZYdA2OIHsrgmlr1KY1mj+CXw3pk+fbo8kYcOHZrA1DPJhRKIQvzQ54dX0NAHmDZH8UuoRY877jgplP/4xz8SmgMm2y+BKMQPacSoL0Z/MeMgTY7il1BrPvrooyJ+ePuDLhsEohI/zPdD7Q/z/9LkKH4Jtibe90WhfO655xKcCybdK4GoxA/pwxsfKGt4AyQtjuKXYEvi/UsUyJNOOinBuWDSvRKIUvzWrl0rZQ3v/qbFUfwSbsl+/fpJocTaf3TpJhCl+IEsVnvBwxaLsabBUfwSbkWsmMtFDxJuRI/Jj1r8tm3bJuKHdf/S4Ch+KbDit7/9bSmUWCiSLr0EohY/kMUipKj9YeXnpDuKX9ItqJTau3evfH2Lix6kwJgOWYiD+O3bt0+mveCbH0l3FL+kW/Dz9F9++eXyRJ48eXJKcsRsmAnEQfyQJnzlDbU/fPUtyY7il2TrGdJ++PBhWfCAix4YoKRsNy7ih+/74ju/+N5vkh3FL8nWM6V94sSJ8kS+6qqrTGf4Nw0E4iJ+YDl27Fgpa5MmTUosWopfYk1nnXD0+9WvX9/6JI8mmgCWM+vQoYN69913PW1BZ7ZJkyaJXvSA4hd0CQk5/jvvvFOeyN/97ndDvjIvFzQBrK6Cbo3LLrvMdbv00ktLlhwMqL355pt18X300Udqzpw56sILL5Syhv7mJDqKXxKt5pLmjh07SqF8/fXXXXzydJIIQPywnJmbO3LkiDr//PPdvHk+/+yzzyqsI/nKK69IjfOuu+5SK1eulPC6pQFBTJqj+CXNYh7S+/DDD4v4cdEDD7AS5CUq8QMifMgc/XvoTzZ+1nLevHlS1gYNGpQgkv9PKsUvcSbzluAePXpIoXzxxRe9BaCv0Angk6QrVqxQ999/v6qpqVH79+93TEOU4oeE3XfffQrfkVm6dGlOOrt06SJvGe3cuTPneNz/UPzibqEC07dq1SoRPy56UCDAgINVVlaKfVq3bq3Ky8tlv0+fPqq2ttb2ylGK39/+9jeFz6Z+8sknau7cudLnh324NWvWSPr79u1rm/Y4nqD4xdEqJUoTCiMmo5qf1CWKntEUSGD48OEKomdcIAC1Poig08fCwxa/BQsWKLzPC4fVw9Hnp92yZcv0rvz27t1bytrGjRtzjjv9QdnUG/KN79KgNhyWo/iFRTqC67z88stSuLDqM108COD9a9zwVjU8iCHOLV++3DKxYYrfwYMHpSmOpi7m9I0aNUrt3r3bMl04uHXrVkl79+7dbf0YTyD/yCsEFvlGnrX4uzX/jfEUs0/xK4ZeAsKed955UshmzpyZgNSmP4mo8VVUVNhmFIIwbdo0y/Nhip8xARCoqVOnqqqqKnX33Xerp59+2ni6bv/ss8+WsrZkyZK6Y3Y7iBN5NTot/sYasfF8qfdzr17q2AOKDwWoXbt2AcWermjfeecdmfTsZYpEunIev9zo2o7TzW0nfvqNCnxLw+397VJPdUFtdfv27QIUS6i99dZblnD37NkjAx+YZI8J2RgcsfvuBx4AWCHG6LzwMfovdp/iVyzBBITHhFfcVLfddlsCUpveJKJGZ67tmHNrJX7jxo2TcDinN3xVzc6VWvxuvfVWdeDAAbvL1R3XU6x0GvFrN9kaTVwM+hgd+KBiw2avkYppnzU/ExCXv4cOHVJ4FYmLHriACvi0m/jpmo+5zw/l3Sgo2McCto0bN7bdUPtq0aJFSbaGDRt6igeLHZjTif///ve/88jiOOYNYooPpvtgsAPH0BwOy7HmFxbpiK+jm01c9CA6Q0D82rRpY5sAu5qP/kypUVggbhBFpw1r7oW5QYyNacQ+BNH8wXPdt2f0ixHwMEd6YQSKn21RTN8J3CgojHTRENAjvVY3OZp6EEarwRAMNBiFAvuYaxc3hxqrOZ0TJkzIS6YWeX0CwmeVb30+qF+KX1BkYxjv7bffLoVz2LBhMUxd+pMEgcMDaMSIETmZxXFMcMY5u/4uCCdGU/Ht3Pnz5+eEj9OfJ554Qg0ePFjhw1p2/ZIQO+Nghx75tct7UPmj+AVFNqbxHnvssSKAGAWmC5+AvtExqRd9XujrQo2vrKzMcu5f+CkM/orIK2p/2kH0UGMMs78P16b4aQtk5HfWrFlS0M4666yM5Dh+2USzFyOdqP2gtoeaUNi1nqioaKEzT/cBA9R+w3QUvzBpx+Ra3bp1EwHcsmVLTFKU3WTofkCzGKSVCEa0IfpmsUd/odXxIDlQ/IKkG9O4dcd0r169YprCbCULtR40fc2CUCwFCCqa1gMHDpTmdXV1tacoUTPFIAua5AjvNZynyGPkieIXI2OEmRQ0MdDPohelDPPavFYuAYgehMpqFDjXp/d/ekQVo6jY1//dmpa6TxKCjDBonqNpDiFMm6P4pc2iHvODJYogflz0wCOwhHlD89Jck7SbRG3MGvxgMzrdUjAfN/pJ4j7FL4lWK1Ga0ccCAZw9e3aJYmQ0cScAe6Of0a9DuLT1S1L8/JaCFPl/4403FF6U56IHKTKqQ1Z0k9Zv81rXGFnzc4Ab1in0QXBVl9LQxoRbPNUxAZoufQTQb6cHLzC/rpC5dOj/QyshbY41v7RZ1Gd+8NUtvJPJRQ98gkuId4gWNggfRn39jtxCLFHZSFutD+aj+CWkEAeZTCx2gNrfNddcE+RlGHfEBNBnByHz2uenm8lp6+vTZqD4aRIZ/23ZsiUXPchAGbBaRNQq21r4CmkmW8UXx2MUvzhaJYI0YXVg1P7Qv0OXXgJe+u+yIHywMMUvveXcd86w9hsE0Dw/zHdEDBA5AczNMzs0X2FfY7N3ypQp6sYbb6zzCuFLax9fXSY/36H4mYlk+D8+no2bA0sn0SWbAAQMtsQgBzb9Ro956XjMmoA/vdoy9u22tI34UvySXcZLnnostYTCj89e0iWbAGp6qOVhw77V/D7U9IwLo8Kf3Za2EV+KX7LLd8lTj88OQvy46EHJ0TLCmBGg+MXMIHFIzsknnywCuGrVqjgkh2kggUAIUPwCwZrsSF944QURPy56kGw7MvXOBCh+znwyexYrPaP5O2fOnMwyYMbTTYDil277Fpy73bt3y7dhuehBwQgZMOYEKH4xN1CUyRs6dKjU/qZOnRplMnhtEgiEAMUvEKzpiPTAgQOqYcOGqlmzZunIEHNBAgYCFD8DDO7mExg9erTU/rjoQT4bHkk2AYpfsu0XSuqbN2/ORQ9CIc2LhEmA4hcm7YRe66c//anU/rDwKR0JpIUAxS8tlgw4H/odUCx+SkcCaSBA8UuDFUPIwz333CO1Py56EAJsXiIUAhS/UDCn4yJ44wMTn7dv356ODDEXmSZA8cu0+f1l/ve//72IX+/evf0FpG8SiCEBil8MjRLnJPXs2VME8M9//nOck8m0kYArAYqfKyJ60ASw4MHIkSNF/Lp06aIP85cEEkmA4pdIs4Wb6M8++0w+eXjvvfeqnTt3qv79+4sAGhfBDDdFvBoJFE+A4lc8w1THsHfvXvWrX/1KPfHEE3X53LFjhyx6wA/H1yHhTgIJUPwSaLSwkvz++++rn//85+rpp5/Ou+QFF1wgtb9p06blneMBEkgCAYpfEqwUUhqffPJJtWbNGrnaJ598ou6++261du1ay6u/99578sobFz2wxMODCSBA8UuAkcJKIgRt5syZ6qGHHlIPPvigWrZsmeOlR40aJbW/a6+91tEfT5JAHAlQ/OJolYjThBrfeeedp1566SXHlGAgBDW/Bg0aOPrjSRKII4FEih9WGWnRooXCpFsvG25SOm8E9u3bp66//nr5fCEWMV26dKljQPjFWx8XXXSRoz+eJIG4EUik+DVt2lTED98cddvQMU/xcy52q1evVgcPHhRPjz32mFq5cqXsHzp0SKa4HDlyxDGCtm3bigB++umnjv54kgTiRCDR4ucFJMXPmRL6+RYtWqTGjx8vHyv68Y9/rCB6ftxdd90l4vfNb37TTzD6JYFICVD8IsUfn4t/8MEH6mc/+5m65JJLZMDj1Vdf9ZW4Tp06iQC+9tprvsLRMwlERYDiFxX5GF731ltvVW+//dsh3o8AAAUmSURBVLbCa2wY9PAjZPPmzRPx46IHMTQsk2RJIHbiV1tbq2pqaiwTqw/qPj/93+mXzV4nOl+cg9Bhzb5iXI8ePUQA9VxBL3Ht2rVL7A2b623//v1egtIPCRRFIFbih0Lfpk0buYGcckXxc6JT2LmnnnpKYZJzMQ4DJxj59bPowfDhw1VZWZkaMGCA/CI8ysCGDRuKSQrDkoArgViJH16Vwk2AGwA1AjtH8bMjU/hxTG7etm1b4RF8HvK0004T+6EZ7MW1bt1aGV+RwwOwvLxc9enTx0tw+iGBggnERvwgdvqJD/Gze/LjtatGjRqpJk2aeMo0m72eMMlgBxYxKNZBQGE/iBqmITlNlIbNrWwNMcRxOhIIkkBsSlhFRYXU+pBZFHzcOGa3efNm1bFjRzkPP926dVNuo5IUPzPF/P+Yxzdu3Lj8EwUeQbMX9tFbZWWlZUzLly8XP+Y+PjSF0QKgI4EgCcRC/DDIgRtF1/bQ7DE2hTSAwYMH191Q+sZCMwvrytltvXr1UrNnz7Y9bxcuS8fR5MVDohR5njJlSp6NYKu//OUv2ox1vxDFrl271g10VFdXq4EDB0rfH8oEHQkESSAW4oenvPFJj33UBM2uVatWljeWFkL+flHbihsLLJRgdrCzOZ0QP3NN0ByO/0mgFAQiFz/U9nAD4IPYVVVVsqGz2yiGOqPnnntu3s2Cmt306dMdN6xAzC0cBnhTxCxo+K9r9dqW+MXxGTNm1B2C6MHuHOyoQ8KdAAlELn5o4uqpDij42PAfzSGze+aZZxQWNdA3F1YSRj8gXbwIXH311XU2gq3GjBmTl0Dd1WFu3uqHoZVY5kXCAyRQBIFIxQ+DGrg5zNNa9HGrfO3Zs0fNnz9fBkSwAgldPAmsX79e3XfffWrdunWWCbSzsR4EMZcJy0h4kASKIBCp+KGGZ9W3p5/+vAGKsGzMgxpH93VSYW80edEaoCOBoAlEJn4YzcVcMKvObdwEqBGy6RO0+aOLHwKHeZ0Y4NAbbI5uDz70orNLlq4cmfihoxtNHDsHceRNYEcn+cdhX+OGZrC5/y/5uWQO4kwgMvGLM5Qw0wYB0O8zo+aDWhBFIEwL8FpZJUDxi9DyqP2i6a+b96jpotlnNdIdYTJ5aRJIJQGKX4RmhdCZX/2ymwISYTJ5aRJIJQGKX4RmxTusaOYanZ7qYTUQZPTHfRIggeIIUPyK41dUaNTy0OydNGmSjHqj+Yv+P3NtsKiLMDAJkIAlAYqfJZbwDmoBxGAHNox60pEACQRPgOIXPGPbK6Bpq99jhuihDxA1PwqgLTKeIIGSEaD4lQyl/4ggduj3MzoIH2qAegTYeI77JEACpSNA8SsdS18xOb3FYreeoa8L0DMJkIAjAYqfI57gTqLJixqe1VsuFL/guDNmEtAEKH6aRAS/aPKiz2/FihVyddQGMfKLEWC+2heBQXjJTBGg+EVobtT+sLoJxE6P9qIfkP19ERqFl84MAYpfZkzNjJIACRgJUPyMNLhPAiSQGQIUv8yYmhklARIwEqD4GWlwnwRIIDMEKH6ZMTUzSgIkYCRA8TPS4D4JkEBmCFD8MmNqZpQESMBIgOJnpMF9EiCBzBCg+GXG1MwoCZCAkQDFz0iD+yRAApkhQPHLjKmZURIgASMBip+RBvdJgAQyQ4DilxlTM6MkQAJGAhQ/Iw3ukwAJZIYAxS8zpmZGSYAEjAQofkYa3CcBEsgMAYpfZkzNjJIACRgJUPyMNLhPAiSQGQL/AxekJ4Px4x12AAAAAElFTkSuQmCC[/img][br]
Write a sequence of transformations (dilation, translation, rotation, reflection) to take one triangle to the other.
Write a similarity statement about the 2 figures, and explain how you know they are similar.[br]
Compare your statement with your partner’s statement. Is there more than one correct way to write a similarity statement? Is there a wrong way to write a similarity statement?[br]
IM Geo.3.6 Practice: Connecting Similarity and Transformations
Find a sequence of rigid motions and dilations that takes square [math]ABCD[/math] to square [math]EFGH[/math].[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUAAAACsCAYAAAAKYXXnAAAUSElEQVR4Ae2db2he1R3H2w3RUSGxG7ULzoS60rIXS3zRLX1jorLXiXslMklkiINVE+oLS4dLYE6LK026tY4SR6JlA/FP6rBFx0YyNos2pWlEq8Jq1YmDBRc6us4X0zO+t56H58997rn3ec459/z5Hrg8f+6f8/t9f/f5POee373nrBMsVIAKUIFIFVgXqd90mwpQASogCECeBFSACkSrAAEYbejpOBWgAgQgzwEqQAWiVYAAjDb0dJwKUIHCAJyamhKzs7NULlIFFhYWxOTkZGU5duyYWFtbi1QNuu27AoUAiJN/3bp1YmBgwHe/aX+LCgwNDYnu7u7kHMB50NHRITo7O8X8/HyLR+RuVKA8BQoBECc8FpzwLHEqAPhNTExUnEfrD1DEOcGWYEUWvvFEgdwAxD88/u3xilYgS3wKAHCIPa4Eqov8Ht0jLFTAJwVyk0z+81+4cCH5ESwvL/vkJ23VoIDsAklr6cnzQ0M1PAQVsKZALgAi6YHWnzzx01oB1ixmRaUpgEvf3t7e1PrRNTI2Npa6jl9SAVcVUAIQ0EP/TvXlDf7tqz+76hzt0qsAIDcyMpJ6UPwpVvcNpm7EL6mAYwooAYiTGid3/cKT3bFIWjAHVwFpf3zoDuFVgYUAsArtCmQCULb+ADv0/8gFLQFk/ljiUSCr71feGhOPGvQ0FAUyAYjLHVzu1hcAERBkiUcB9AOjlVdfcI6w9VevCj/7okDjGf2F5fIfv/6WB6zGZRDvBfQlxHrsRIKjr69PLC4uJsvc3FzyWd4apacWHoUK2FWgKQDRwmvWypO3Q9g1lbWVqQDOBdkPDOjhM/4I8UfJQgV8VaApAH11iHZTASpABfIqQADmVYrbUQEqEJwCRgD4zjvviM8++yw4sUJ36Pz58+LSpUuhu0n/qEBFAa0AfOmll8SWLVuSvqINGzaIAwcOVCriG3cVOH36tLj55psrfXx79uxx11haRgU0KqAVgF1dXZUfkewwX1lZ0WguD2VCgZ07dzbE7cUXXzRRFY9JBZxSQBsA0YqQ0Kt+3Xbf18Xtx77FxVENbjm6LTVuDz74oFMnKo2hAiYU0AbA1dXV1B/S4WcOirOrp7g4rMHXrv9qQ+yeeOIJE+cbj0kFnFJAGwDh1d69e2t+SHfccYdTztKYdAUOHTpUE7f+/n7x+eefp2/Mb6lAQApoBSB0wU3SN929SRyYezwgmcJ3ZWlpSXxz9Hrxo1+kj/YSvgL0MEYFtAMQIqLPD5e9LH4pgLg99fYhv4ymtVSgDQUIwDbEC21XAjC0iNIflQIEoEqhiNYTgBEFm64mChCAPBEqChCAFSn4JhIFCMBIAp3HTQIwj0rcJiQFCMCQotmmLwRgmwJyd+8UIAC9C5k5gwlAc9ryyG4qQAC6GZdSrCIAS5GdlZaoAAFYoviuVU0AuhYR2mNaAQLQtMIeHZ8A9ChYNFWLAgSgFhnDOAgBGEYcXfUC88eMjo4mk2lhxChMsoXPmFe6rEIAlqW8g/USgA4GJRCT5LSqmEwL7zFmAF4xp3TazJO23CYAbSntQT0EoAdB8tDE+fn5ZLQhAM+1QgC6FpES7SEASxQ/4Kq7u7vFyIibowwRgAGfeEVdIwCLKsbtVQrI1p+r80cTgKoIRrSeAIwo2JZcRcuvt7e3pjYkPRYXFytLzUrLHwhAy4K7XB0B6HJ0/LQNSQ8kOqrL2NiYwPe4NK6HY/V2Nt4TgDZU9qQOAtCTQHlkJkAH4KWVrHVp25v4jgA0oaqnxyQAPQ2cw2YDcljSCu4FLDszTACmRSbS7wjASANv0O2pqankFpj6e/3QDwgAlnkTNNwmAA0G37dDE4C+RcwPe9HPB9iNj4+L6elpMTk5KYaHh0VHR0fpDhCApYfAHQMIQHdiEZol8qkPeUmMfsH6VmEZPhOAZajuaJ0EoKOBoVnGFCAAjUnr34EJQP9iRovbU4AAbE+/oPYmAIMKpxVnPv74Y3HqlL9zgBOAVk4TPyohAP2IkytW7t69O0luIMHR1dUljh8/7oppue0gAHNLFf6GBGD4Mdbl4YkTJyrwAwCxbN26VdfhrR2HALQmtfsVEYDux8gVCx9++OEGAAKC58+fd8XEXHYQgLlkimMjAjCOOOvw8jdHf9sAwM7rrtNxaKvHIACtyu12ZQSg2/Fxxbrl1f+IzieXxFV9t9RA8IYf/kSsffo/V8zMZQcBmEumODYiAOOIcztezr/3rwR+vc+8IS78+1PxyiuviJmZGTF/cll0zCyJ0T/xEljgh3R21d/UeDsniM/7EoA+R8+87dMr/xDrDr8mhk68m9rSm337n8n6iVN/N2+MphrYAtQkZAiHIQBDiKIZH9CyA/zG/vJ+ZgWAH7YDDH0oBKAPUbJkIwFoSWiPqkGfXt8zbxSC2sgf/5Zsj75C1wsB6HqELNpHAFoUO0dVGE6+fjRl7Ib5NXDLiemhpACwnqev9O0VgRmgiT5CJErQT+hyIQBdjo5l2whAy4IrqsOQ8RMTEw1bYWQVANBkqU92FK0LEOx+ejlpPbqcGTaiIn5ITIIUPWXK354ALD8G0oK1tbUEcmlDRsk5NeS2ul9VyY689aHViMzw8Il38+5ifTsC0Lrk7lZIALoTG4APrTyAsL5gTL20lmH9dq18lskO9OPpKGhJ5kme6KirlWMQgK2oFug+BKA7gQXgms2YBjBivl2dBZepg8fOFUp25K1/6uyV22dMZYbRJ4pRpuuXtNZzvc0EYL0iEX8mAN0JPlp5AF2zRedE47hURaYXl6sLH100IoLMDJs4PuYdwfD6crRp+UoAGglluAclAN2JLX7Q+GHXF3yH5IiuAiAhW4usbZFMbyv1y8yw7nqQKU/LluexkS3APCpFsg0B6Eags25zaXZrTCuWyyc3BubPpT7Z0coxs/aRt8egtakzM9wsW55li1xHAEol+Jo8wvjU24eoRMkKoH8Pl75pBf2COhIgupMdabamfSczw+hv1FGysuV5jp+ucp49M7ZBS4K3wWQI5OgqtgDdCEyz21za/bHDO5PJjrzq4bIbmWEdAyfIP4u0bHkeewjAPCpFsg0B6Eag0YkPCNaXrFtj6rdN+2wj2ZFWb9p38vIbGeJ2ClrDaYmivMckAPMqFcF2BKAbQcaPOi2Die/SEiN5rLaZ7MhjD7aRmWHcK9hqwZ8FEiDQRi5FHhFUAjCNrqg0q/ASOEsdd9cRgO7Gph3LZGsLWVidyYd2bJL7IgGDLHSrmeFm2XJ5fNVrLgDiX0fSFa8qwhKAKtndXE8AuhmXdqwa/+v7SX+bric72rElbV+ZGcagC0XhnJUtT6sr7btMAMpO16IdjARgmtTuf0cAuh+jLAvPnTsn9u7dK3bt2iWe/f3x5BlcJBva7WfLqlPHOowYg5uwcXtMkaJjUIhMAKK11ywdn2UoAZiljrvrCEB3Y6OybGVlRVxzzTU1CYGv/GCPaKd/TVWnzvW4BC6aGW6WLS9iVy4AVj9jByiqCgGoUsjN9QSgm3HJY9UDDzxQAz80XLZs255nV2e2kX2VNofUzwQgrrGRYUFWCgveQ9jR0dFM0QjATHmcXUkAOhsapWF33XVXAwA3btyo3M+1DTDkPlqCgKGNkgnANAOQAAEEcf3drBCAzZRx+3sC0O34ZFl39OjRBgB+/+57snZxdh0mXZKZ4YsXL4rLly8bs7UwAGGJ6nEcAtBYvIwemAA0Kq/xgz/yyCOiq6tLXH311WLj4JDoPPJa4cyqcSNzVIBs8Ld/d0ZcteN7Fajfe++9OfYsvgkBWFyzYPcgAMMJLSAiM6tFby9xQYX7fryrAj9ccWLZt2+fdtMyAZh2+4tMPWeNR8YWoPY4WTkgAWhFZmuVyIEHdDxza83oLyraunVrAwBvvfVW7WZkAhCJj56eniTpMT4+Lvr6+pKBB7P6/2AhAag9TlYOSABakdlqJWVkVnU4uHPw9gYA3nOP/j7NTADCEcBOZoHxPqvlJx0nAKUSfr0SgH7FK6+1vk1WDmhvGJuuAeC1114rTp8+ndfl3NspAZj7SFUbEoBVYnj0lgD0KFgFTZUDD7T6zG3B6lrefPLUR5VH906eWRGPPvqo2L9/v/jggw9aPmbWjgRgljqRrSMAww04EiFySHpXJyuXg7TiXkBbhQC0pbQH9RCAHgSpDRMBQRcnK4ddeA7Y5g3QUkYCUCrBVw6JH8E5IDPDrkxWDnswEgxu2Snj8pwAjOCkz+siW4B5lfJ7OzlZedm3x8AOOSNdWZflBKDf57JW6wlArXI6fTDTk5WrnJ9euTJZOh57K/NGbQJQFamI1hOAEQW7akh6E5OVZylZRrKjmT0EYDNlIvyeAIwv6O0OSV9EsTKTHc3sJACbKRPh9wRgfEEHlHB7jO7JyuuVLDvZUW+P/EwASiX4yixwpOeAzAzrmqy8XkYXZ6STNhKAUgm+EoARnwM6JyuvllE+i4xL7TKTHdU2Vb8nAKvViPw9L4HjPgEkrHRNoiSTHa7OSIdoE4Bxn/M13hOANXJE+UE+M9zOZEpo6eFyuownO4oGjQAsqljA2xOAAQe3gGvVQ9IX2C3ZFP2JSKjgyQ7bt9cUtRXbE4CtqBboPgRgoIEt6JbMDBedrNzlZEczCQjAZspE+D0BGGHQm7hcdLJy2X/YbrID0+4uLi4KTL5moxCANlT2pA4C0JNAWTITl7N5JivXkeyYmpoSnZ2dyYRrAwMDycjzg4ODxj0lAI1L7E8FBKA/sbJlqWzZpU1WrjPZgVHn0fqTBSPPd3R0CIDRZCEATarr2bEJQM8CZslcOVn5T5/9QzIzG6bGeO/ifyvJjnYyxlkujIyMCLQGTRYC0KS6nh2bAPQsYBbN7R//Wc0cHV++cZu48cnXjI7hB/gBgiYLAWhSXc+OTQB6FjCL5t7wjRtrAIh5en/++H5jFuASGHVUXxabqIwANKGqp8ckAD0NnGGzL1261AA/wOn+++83UjPmI8cUvKZbfzCeADQSQj8PSgD6GTcbVt92220NEHzuueeMVA3w9fb2CoDQdCEATSvs0fEJQI+CZdnUN998U/T39ycQXL9+vXjooYeMWGATfnCAADQSRj8PSgD6GTebVn/44Yfi8uXLRqq0DT84QQAaCaWfByUA/YxbCFaXAT/oRgCGcPZo8oEA1CQkD1NIAWR6kVRptpjMBBOAhUIV9sYEYNjxbebd0NCQwGNn1QtaZLYKkh2AXLPFZDKEALQVZQ/qIQA9CJJmEwEXtLzwyFk1gGwNRqDZncKHIwALSxbuDgRguLFt5hmgBwDGWox4jh/S2dVTsWrqrd8EoLeha9lwDEKAe+5iLQRgrJFP8ZsATBEl8K9sPG/rsoQEoMvRsWwbAWhZcAeqw5BT9dlXtApjKQRgLJHO4ScBmEOkgDaRAw7UJ0DwfSyFAIwl0jn8JABziBTQJvPz81EnQBBKAjCgE7pdVwjAdhX0a/+xsTHjA466rggB6HqELNpHAFoU24GqkAABBGMuBGDM0a/znQCsEyTwj0h+9PT01DwBEhsQCcDAT/Ii7hGARdTye1s8AYJsb/2CfsGYCgEYU7QVvhKACoG4OjgFCMDgQtq6QwRg69pxTz8VIAD9jJsRqwlAI7LyoA4rQAA6HBzbphGAthVnfWUrQACWHQGH6icAHQoGTbGiAAFoRWY/KiEA/YgTrdSngBEAfmdqizj5/p/1WckjWVHgu7+8SRw6uc9KXayECriggFYAYp7QzZs3J88Xrv/SevHYY4+54CNtUCjw6quviu3bt1dGBRkfH1fswdVUIAwFtAJw06ZNlR+RHGLnzJkzYSgVsBc7duxoiNvzzz8fsMd0jQpcUUAbAJeWlhp+RIDgtvs2C/QtcXFTg1ue3pYat927d/M3QgWCV0AbAD/55JPUH9Kvn/1VMjw+hsjn4qYG13c1ttyPHDkS/MlPB6mANgBCysnJyRoI3nnnnVTYAwVmZmZq4oZRQlioQAwKaAUgBHv99dfFwYMHxcsvvxyDfsH4+NZbb4nDhw+LF154IRif6AgVUCmgHYCqCrmeClABKuCKAgSgK5GgHVSAClhXIBcAZ2dnk/499PHJJaaJU6xHxYMKMZ7c9PR05XyYm5vzwGqaSAVqFcgFwO7u7mTuADl4Ij7jFpfl5eXao/FTFArgPED8MaH20NBQcm5gekX8UbJQAZ8UUAIQ//Q42RcWFmr8AgRjGz67RoBIPyDmgF39+RCpHHTbcwWUAMSJDgAChNWFE6pUqxHHe3kuEH5xxDsGL5UAxOUOLnWqi5xPlD+EalXCfy8vd8P3lB7GooASgGjpdXZ2VmaO6uvrS/p9CL9YTpErfsquEPbzxRX30L1VAhD9PfjnlwmQkZERgf4/JkBCPzVq/ePlb60e/BSGApkAxK0uadleQBAtQZZ4FJAAjMdjehqDApkAlH199UKgNYhWIEs8CkgAsuUfT8xj8DQTgLjlIe3BeHn/VwwC0ccrCsirAfz5sVCBUBTIBCDgNzw8LBYXF5MFT4EMDg4m94HxSZBQToH8fuAPEQkxPAEib4tCyxALCxXwUQElAAHB6mVqaqpy8vvoMG1uTwG0ANEvXL0wM9yepty7PAUyAVieWazZdQVwBcCrANejRPtUChCAKoW4ngpQgWAVIACDDS0dowJUQKUAAahSiOupABUIVgECMNjQ0jEqQAVUChCAKoW4ngpQgWAVIACDDS0dowJUQKUAAahSiOupABUIVgECMNjQ0jEqQAVUChCAKoW4ngpQgWAVIACDDS0dowJUQKUAAahSiOupABUIVgECMNjQ0jEqQAVUChCAKoW4ngpQgWAVIACDDS0dowJUQKUAAahSiOupABUIVgECMNjQ0jEqQAVUChCAKoW4ngpQgWAVIACDDS0dowJUQKUAAahSiOupABUIVgECMNjQ0jEqQAVUCvwfDmKDUH7SqOQAAAAASUVORK5CYII=[/img]
Quadrilaterals Q and P are similar.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAU8AAAEECAYAAACoUrZdAAAgAElEQVR4Ae2dB7gURdaGBRGWHCUrWUBYdAFlyUiSDAIShCVIFCSukqNkJEqOklF2JQkSRQQEAQkCSkbCkkQkBxGt//nKvy83TOiZ6VDd/Z3nmTtzO1Sdeqvnm+rqqjpPCRoJkAAJkEDIBJ4K+QyeQAIkQAIkICievAhIgARIIAwCFM8woPEUEiABEqB48hogARIggTAIUDzDgMZTSIAESIDiaeM18NNPP4lUqVKJsmXL2ugFsyYBEgiHAMUzHGoGnfPSSy+JbNmyUTwN4slkSMBKAhRPK2lHy2vgwIFSNLX3aLv4kQRIwAEEKJ42VNJXX30lUqZMKXDbTvG0oQKYJQkYQIDiaQDEUJK4ceOGyJ49u1ixYoU8jeIZCj0eSwLqEKB4WlwXzZs3F7Vr147KleIZhYIfSMBRBCieFlYXWpt4QITWp2YUT40E30nAWQQonhbWF/o569SpIwYNGhT1KleunLyNxzb0hdJIgAScQYDiaWE9YTxn7BdaohBVbP/4448t9IZZkQAJREKA4hkJPQPO5W27ARCZBAnYQIDiaQP06FlSPKPT4GcScA4BiqfNdYWxngcOHLDZC2ZPAiQQKgGKZ6jEeDwJkAAJCMHFkHkVkAAJkEA4BAxveR49elTMmDFDrFmzJhx/eA4JRBHYu3evmDx5stiyZUvUNn4gAVUIGCqeEM2nnnoq6lW5cmVVykk/HEZgwIABUdcRrinMzKKRgEoEDBXPDBkyxLjgcdH37NlTDv7GAHC+yEDPNfDZZ5/FuY5wLW3dulWl7w598TgBw8Tz4sWLPi/46C1Rfn7SKieL0FnMnDnT419XFl8lAoaJJwqFxX1ji8KqVatUKi99UZwAhm41a9YsznWE6+rQoUOKe0/3vETAUPHEbVXu3LmjLvw333zTSyxZ1ggJDB48WMSPH1/kyJFDNG3aVKRNm1ZeS9g2atSoCFPn6SRgLAFDxVNzDYO+0VJApz+NBIIRWLBggciVK5dIkCCB6Natmzh9+nTUKd999524c+dO1P/8QAKqEDBFPFG4ggULijJlyqhSTvqhIIHt27eLihUryh/aBg0aiG3btinoJV0iAd8ETBPPESNGyC8F+6l8g/fy1gsXLojWrVvL66NkyZJi6dKlXsbBsjuUgGniiS8Ibt0/+ugjh6Kh22YQGDZsmEiYMKFcw3TMmDHiwYMHZmTDNEnAdAKmiSc8T5Mmjahbt67phWAG6hNYsmSJyJs3r/xB7dq1qzh16pT6TtNDEghAwFTx7Ny5s0idOrW4dOlSABe4y80Edu3aJapUqSJFE6Mvvv76azcXl2XzEAFTxXPPnj3yS4NWB81bBDBpon379rL+S5QoIXgNeKv+vVBaU8UTANHv2bZtWy+wZBn/nwDGZCZJkkRkyZJFfPjhh+L+/ftkQwKuI2C6eOJWLU+ePOLRo0eOg4fZLhj4jxc+0wITWLZsmShQoID8wezSpYs4efJk4BO4lwQcTMB08cT0TLQ+N27c6DhMiK8O36O/Xn75ZUa5jFWTWDquRo0aklP9+vW5gEcsPvzXnQRMF09gg/j07t3bcQQR1RLz9bWVgBDdEtEuU6VKxZaoEPJBYKdOnWT9Fi9eXCxevNhxdUyHSSBcApaIJwZC48vlJMNtOkQfAdqi24oVK3xuj36MFz6PHTtWpEiRQjz77LNi9OjR4t69e14oNstIAlEELBHPadOmScHZv39/VMaqf9BEEq3O2OZLVGMf49b/ly9fHrV6Fvo1T5w44daislwkEJCAJeKJhR0gOGitOMUgDPD5xo0bMVyGmHpRPNGvWadOHVn2evXqsd83xlXBf7xIwBLxBNicOXOKmjVrOoZx2bJlZf9mbIexHeLplafvmOCAlY5Q5iJFiohFixbFRsL/ScCTBCwTTyxPlzhxYnHu3DlHgIZYlCtXLmqo0oQJE+R8bC+1OidOnCin2OLBGcZu3r171xF1RydJwAoClokn+sYgPPPnz7eiXBHloa1HCn+jvzB0yVcfaESZKXgyhpehlYmyY4rt8ePHFfSSLpGAvQQsE08UM1GiRKJly5b2llhH7hiSBOEYP368J8RSQ4KFhzFOE2VH/yZD/mpk+E4CcQlYKp5t2rSR/YiqD2tBmFsIiFfs8uXL4v3335dlxiLWCxcu9ErRWU4SCJuApQqBFXUgSmvXrg3bYStOxMB4PBjygk2dOlUgZDT6o0eOHMmQF16odJbREAKWiic8hniilaOywUcMVXKzoV+zWLFisj4wS+jYsWNuLi7LRgKGE7BcPKtXry6KFi1qeEGMSlAbx4l+Tzca+jUbNWokRbNatWriyy+/dGMxWSYSMJ2A5eKJeDVo2e3evdv0woWTAcQTUzLdNo4T/ZpYXwDsX3jhBYGIlTQSIIHwCVgunnAVX2D0r9GsIYDpsVhbE/HPEZjv9u3b1mTMXEjAxQRsEc/ChQvL0Awu5qpE0VavXi2wKAt+rNq1ayeOHj2qhF90ggTcQMAW8Rw3bpz8Qp8+fdoNDJUrw759+0TTpk0l4woVKojNmzcr5yMdIgGnE7BFPH/++Wf5xZ49e7bT+Snl/5UrV0S/fv0k2+zZsztiNpdSAOkMCYRAwBbxhH8YW4jWEc0YAujXxELNuEVHbPRbt24ZkzBTIQES8EnANvHEWM/06dOLmzdv+nSMG/URQL8mFjCBaGLq648//qjvRB5FAiQQEQHbxPPgwYPyC79y5cqICuDVk9Gv2aJFC8mwdOnSYtOmTV5FwXKTgC0EbBNPlBatpa5du9pScKdmin7N/v37y2FHmTNnFvPmzXNqUeg3CTiagK3i2aRJE4GFKGj6CEyfPl3kypVL/uhgfVR/XR5YUk9b9R0/UHjh1h7baSRAAsYQsFU8161bJ7/YO3bsMKY0Lk3l888/FxUrVpSs8IPzww8/BCwpZkhFnyWF2VJY7ARhk2kkQALGELBVPFEEtIqGDh1qTGlclgoC5r399tuSERbx2LhxY9gl1Obsu23aadhAeCIJREjAdvEsX768wIv2hMDVq1dlv2bChAlF2rRphRHjYbVooE9y4ScSIIFICNgunnPnzpUtKy6J9lc1ol8zb968kkmvXr3iRO8Mp7KxQlSqVKnixKAPJy2eQwIk8BcB28Xz0aNHUigwyNvLhn7NKlWqSBYIhXHkyJGIcGi36doDo0GDBkWUHk8mARKIScB28YQ7aGk1bNgwpmce+Q/9mq1atZKi+Y9//ENs2LDB0JJDRHHLrj0wih2H3tDMmJhhBLAYN0ZIxH4ZlgETipiAEuKJ6YTJkycXv/zyS8QFckoC6NfEcKMkSZLIsk+ZMsVU1yGaaIUiqB1NfQIIA4NYWvjxi/5S33PveKiEeJ49e1Z+sf/zn/94gvyMGTNEgQIFZJm7d+8ufv31V0vKjbnvGMJEU58AxNOt0QzUp6/PQyXEE64mS5ZMdOzYUZ/XDj1qzZo1Uf2atWrVEocPHzalJL5uzbU+UA6UNwW54YmmTJnSU2GvDQdoQYLKiCeEE7Nn3GgQLK1fEy1OPBwy07QZRXhIhJc224itTjOpG5s26nDChAnyhfUf+KNnLF8jUlNGPHft2iVvY9FCcoth3VL0a6ZIkUIkSpTIsv5GDIRH36Y20yj6bCO3sHV7OXDbHv0FMcWPIE0dAsqIJ5DgAnFL6wj9moUKFZJlevfdd8X169fVqXV64jgCaHniVt4t3w/HVYAPh5USzzfeeEMUL17ch5vO2YR+zapVq0rRxLhNLL1HIwEjCGD4ElqjNDUIKCWey5cvl6Jj1oMUM5GjZdC6dWvpf+7cucVnn31mZnZM24ME0OqkeKpT8UqJJ7Dg1n3SpEnqEAriCfo1cVGnSZNGxIsXT4waNSrIGdxNAqETwAgKxKXibXvo7Mw6QznxfPXVV0Xt2rXNKq+h6c6cOTOqX7NNmzaeGuRvKEgmFoMAHppi+UBttATeIZyYJeZrGFqMk/mPZQSUE8/JkyeLBAkSiMuXL1sGIdSM1q5dG9WviRWh9uzZE2oSPJ4E/BKAQGKAvNbHiXcOmPeLy7YdyoknVkfHrfuSJUtsg6JlfO7cOTF48GDRuXNngQdBePij9Ws+//zzSvio+cp3EiABawkoJ54ofpYsWQRug+00jJVEdE8IufZKmjSp/DxkyBA7XWPeJEACChBQUjz79u0rENzs999/tw0RBrdroqm9QzxV7k6wCta1a9esyor5kIClBLBEJl56TEnxPHr0qBSuSMJO6Cl8oGPat28fRzyffvpp8eeffwY6zdX7Fi1aJHLmzCm54OGFnfXjatAsnC0EtCnUaCzhczBTUjzhNArQp0+fYP6bth/zibUWp/bu1TVHARn9vxoH7R13BzQScAMBhPPWrmvtvV+/fgGLpqx4tmzZ0vZojyNGjBBobcaPH180btzYb6jfgIRdsnPhwoVxLi7tIuP7k35xsnAPiyJFigT89iornlu2bJFfVqy0bpfh6Tq+DMOHD7fLBWXy3bx5s0/xxEiE6OMR+fmvlazIwVkc8ufPH+f6xnTxQKaseMJpCNe4ceMC+W/qvk8//VT6gFt4mhA1atSIcYG1bduWWEjA0QTw3S5cuLAoWLBgjGsb2oMGXCBTWjwrV64s8LLLPvjgAwn0xIkTdrmgXL7z588XpUuXllyUc44OkYBOAocOHRL16tUTWIdCa6DhQTXuMvHC52CmtHji6S5+Ac6fPx+sHKbsb9KkiRwyZUriDk4UFx7qZf369Q4uBV33IoE7d+6I9957T/ztb3+Tk18iiZumtHiicvElXbBggS31/MorrwhMv6TFJZAjRw7bJzLE9YpbSMA/AQRZxMSXunXriu+++87/gTr3KC+eCFvRtGlTncUx7jAMhscK8G6PqxQuMcy3Tps2bbin8zwSsIzAF198IYoVKyZKliwpjAwyqbx4fvjhh3K5t/v371sGGxlpAdPMDglsaaEMzOzLL7+UdwV2joYwsDhMyoUE0G/ZqFEjgXUoRo8ebXgJlRdPtABx646VjKy06dOny3zdFFPJaH7JkycXwQYSG50n0yOBYATu3bsnevfuLcdnv/POO+LKlSvBTglrv/LiiVKlSpVKIL65ldatWze5uLFZ4K0si1l54YHaiy++aFbyTJcEQiYwa9YskTVrVtmviaCSZpojxBNCljdvXjM5xEm7evXqIl++fHG2c8MTAto42IsXLz7ZyE8kYAMBTOLAELoSJUqIpUuXWuKBI8QT/Wq4dd+9e7clUJAJxn8Fm2FgmTOKZvTgwQNZL04Km6IoSroVJoFTp06JZs2aiQwZMlg+E9AR4gmuEM+RI0eGiTi007RVnexcmCQ0j+07GpMYypUrZ58DzNmTBB4+fCjjOUEXsALa//73P8s5OEY8GzRoIJvlVhDSonhikD4tMAGMRsAF/Pjx48AHci8JGERg3rx5AuOMcWe4fft2g1INPRnHiCfCYOBLevr06dBLGeIZWE0Jee3bty/EM713+IULFyQr9H/SSMBMAl9//bWctFK0aFHbJs5EL59jxBNOQ9DmzJkT3X9TPmM5PDzhR58eLTgBLKzglbVOMXStTp06MpolrkdEuURLiGYeAYTEQeyw1KlTC6w3oYo5SjwxQwCT+c02PLHDjASaPgJYfi1hwoT6DnboUYhoib5dCCZW0Uf8dMyyypYtm9zWokULh5ZMXbcRDmPYsGHy2kK/5tmzZ5Vy1lHiiTFciRMnFrdu3TIN4t27d+W0w+bNm5uWh9sS1kZDbN261W1FiyoPBBPCOX78+Kht2gdcK9jH8MAakcjfET0XwxPRr6nqRBVHiac2NGbVqlWR146fFDCwFl+EUaNG+TmCm30ReO6550SnTp187XL8NgimP+FE4dAqTZkype2RDxwPWgixc+dOUaVKFfH3v/9dzJ07V+kiOUo8QTJ79uwCU67MMlQYviirV682KwtXpvvuu+/KkNFuLByEEbfngaxs2bLyugl0DPf5J4AYWfheJ0uWTHaJOGH0huPEE/1rwS5k/1UUfE/Pnj3llwCDb2n6CSCSJn50fvzxR/0nOeBIbYEYX7fr0d2neEanof/zH3/8IRftQFhv9Gs66XvnOPHEUCV8SXfs2KG/hkI4Ek9SzRTnEFxx3KEIljd06FDH+R3IYTwYwvV24MCBQIcJimdAPD53Ynk43J5Xq1ZNbNq0yecxKm90nHgC5jPPPCOb9maARSAoO0N/mFEmq9LEcCUMW3KT1a5dW4pnsDLhgRJ/dINR+mv/t99+K2rVqiVeeOEFMXPmTH0nKXiUI8WzTZs2Aqu8G22Y4oUww//+97+NTtoT6S1evFgKzfXr111TXj0tSoxDROsUQkvzTwDfLwzvwrC2AQMGCEyxdLI5Ujxxy46L9dixY4ayX7dunUwXa3nSQieAYV6oFwwpc4vpEU/t1p5DlfzX+oQJE+Qg93bt2ukKruY/JXX2OFI8gQ9fUqNXeR87dqxMF9PAaOERqFChghxqEt7Z6p2FlhKutRUrVvh0DsOUMBuNt+w+8Uhu6MrBdYHGiZvMseKJTma8jDTEIUdUvWvXrhmZrKfSmjhxohQbtxRae9qO2UUQyuiG/zE9M5C4Rj/eS5/37t0rZwPiR2Xq1KmuLLpjxRNP6nDRRhI6NHaN4hYNHf+08Alo/X9mTmQI37vwztRmEEEoMVRu5cqV8h0tTlyDvF1/wvXSpUsytG+8ePFkvya6ctxqjhVPVAguXCOj4WXMmFG8+eabfusaw1XQd4MvEBeD8ItJFCpUSLhteisEEq0oXHPaCz+2qk4d9F875u1BNxoWJcY8/8OHD5uXkSIpO1o80Uo0akGGI0eOyC8FhNGX4UkqZppAFLQFIdASiX0r5+tcr21DUDi0ytxqaF3jWuAi0H/VMGbj/fOf/xSlSpXy1Mw8R4snWoEIYm+EIe4JWhRYkMCXoeURXSjxGS0RPGmlxSSA/i6wxHg+t5o2393L9Y/1bhs3biwyZcpk+MNbJ1w3jhZPjCfEl9SI1XzQWkJaBw8e1F1vuG3DixaXQLp06cT7778fd4eLtqDucc34exLvoqLGKMrVq1cFQtSg7P379xc3b96Msd8r/zhaPFFJ+JL26NEj4vpCXyf6a3777TfdaaHbwMstj0CgME85T548gQ5x/D7cfaDPM9jUTccXNFoBZsyYIUP7osXppXJHQxD10fHiidZNwYIFowoU7gc85ChTpozu07UhLOj/osUl8MUXX8iWyZkzZ+Lu5BbHEUAYHIT2xcw+xPiiCeF48dQe9ETydA+LK2N8J5b612MQTDwQCbbSjp603HwMbuvGjBnj5iK6vmzoxkJo3zRp0ojJkye7vryhFNDx4onCRvol1aZ7jhs3Lig73KrhKbvbhuIELXgYB9SvX18gpAnNeQQwUQQjTzBeE91iRo6ndh4N3x67QjzfeustGVXPdxGDb502bZoU4LVr1wY8mMIZEE+cnQsWLJBc7927F2cfN6hLAGsT5MyZU9StW1dg5ATNNwFXiCfWAkTr8/Lly75LGWRrx44d5fmB+i8pnEEg+tiNp7Col4ULF/rYy02qEUA/Neago//fyMknqpXTKH9cIZ6AgS8pWjrhWKVKleTagv7O1YQTt+sYFhX7hf003wQwnAcLTNPUJXDo0CHZ34/V3CdNmqSuo4p55hrxxJe0UaNGYeF9/vnnRc2aNf2eqz1Zh0D7enGKnl90AitVJUiQwP8B3GMbAYyTRhx0rK+JWXPh3rnZVgCbM3aNeGKuefLkycXvv/8eElIEnoIgcgHkkLDpPhgxacB3w4YNus/hgeYTmDNnjgztW716dYGIsbTQCbhGPBFICl/S9evXh0QB49dwnpsW8A0JgAUHY7A8FsGl2U8AP2II7ZsvXz72a0ZYHa4RT3DInTt3yLHDR4wYIcXTrIByEdaPK07v3bu3nP/sisI4tBAYD43Qvoj/xbG3xlSiq8Rz2LBhIleuXCGRadKkiVwhx01xd0ICYMHBuC1E6z6UdQMscMsTWWDEAyKaIh46psxeuHDBE+W2opCuEk8EmMKXdP/+/brZFS1a1JRgcrod8MiBeJKLRSRo1hHAcwCE9q1YsaLYtm2bdRl7JCdXiSfqLHHixGLIkCG6qw8PmZo2bar7eB4YHgFMfcX4QZr5BDDuGaF9c+TIIT799FPzM/RoDq4Tzw4dOojixYvrqs7vv/9etlRDEVtdCfOgOAQ+//xzyRphGmjmEDh69KjQJnygC4tmLgHXieeePXvkl/T8+fNByS1atEgey1/noKgMOQBdKlxcwhCUMRK5ffu2wIPP1KlTi5YtW4pAM+VinMh/IiLgOvEEDXxJse5gMOvZs6c8FjMsaOYTwEwjTP+jGUcAs+qKFCkil1NkyGzjuOpJyZXiiXhDeAUzhC7G7KLHjx8HO5T7DSAwd+5c+WOFMbm0yAhs2bJFLtyROXPmsKclR+YBz3aleCIsAqYE3r9/P2ANY1gT5rXTrCGAZc1wV8BFJ8Lnffz4cdG5c2fJccCAASHPqAs/Z54Zm4ArxROFxJc0UGwZLOaBY9DBTrOOwKuvvhr2GgTWealeTljWb9SoUTJUDJZgPHnypHpOeswj14onxm+2adPGb3Vi3BvE86OPPvJ7DHcYT2D06NFyDQLjU3ZviosXL5ahfYsVK8Y48QpVs2vFE0910R/kz7Af4hnqXHh/6XG7PgLHjh2T3PlwIzgvLH2IwIRp06bl2gvBcVl+hGvF8+7du/JL+s033/iEioUqEiVKJLCqEs1aAlmzZpVLoFmbq3Nyw0pUXbt2ldcvRoQ8ePDAOc57yFPXiifqMFOmTKJv374+qxOxdTB1jWY9AUQ8RZgHWkwCEEks2vHcc8+JevXqCbTSaeoScLV4YjUfrP7uyxANEAHKaNYT2L59u2xVURyesF+6dKkoVaqUvF7ZlfSEi8qfXC2eJ06ckF/S2E8mMQMD/Z19+vRRuW5c7RuiMnIKoRD4IWnYsKFc9Yizr5x1ybtaPFEVEMkJEybEqJXVq1fL7fPnz4+xnf9YRwDTCPH02Kt25swZGb0APyLo37xz545XUTi23K4Xz2bNmonKlSvHqCC0eCCq3377bYzt/Mc6AhiDizr49ddfrctUgZwePXokxo0bJ/t8ETfrhx9+UMAruhAOAdeLpxa87datW1F8ECguffr0AgvF0uwhoIVNmT17tj0O2JDrsmXL5Bz0/Pnzi1WrVtngAbM0koDrxROw0MJZsmRJFLcXX3xRds5HbeAHWwi8/vrrokaNGrbkbWWmGC6HWUEIgYFoojR3EPCEeGIlH23BYywCEj9+fNGqVSt31KCDS4Gge6gLt9rZs2cFhmVhPDHiB2FKMM09BDwhnli3E0OTYAcOHJAtUcwTptlL4OrVq7IusFCymww/0HhIiaih6G8PJSyMmzi4vSyeEE9UIm7dN2/eLJfvwueVK1e6vW4dUT5MVMCTd7fYf//7X1GuXDn5QAh9nDT3EvCMeCJOdffu3eVtFMQTIQto9hMYPny4XCnIfk8i8wARQtE1hGsLZaK5n4BnxBO36Xnz5hVVqlSRt1N//vmn+2vXASVEPHEIzu7dux3grRBYhBiTK7AaF8JfIJQv5p8jtO/bb78trl275ohy0MnICXhGPH/++Wf5JU2SJIkoWLBg5OSYgmEE0B8NAVLdMD4TQq+9MNwtd+7comzZsgItT5q3CHhGPF977bWoix4Xf4MGDbxV0wqXFt0pTvhBy5gxY4xrCNdR48aNFSZL18wk4Anx3LhxY5yLHhc+bhlp9hPAupWoDwztUdWwkjt8jP3C1EqaNwl4QjwRWjj2RY//d+zY4c1aV7DUqA/VB5BXrVo1znXktmFWCl4ayrrkCfFE4DH0dUYXUK4nqdY1iSmzGOKjsqFljNlpuI5SpUrFp+oqV5YFvnlCPMFx3bp1Mg5MwoQJZexwpzzdteAaUCILRNSEKAWLeGq3s126dJETLhiu2u6asD9/z4in/ajpQSACWG0I4onZYCobhrqVKVNGZRfpm0UEKJ4WgWY2wQlAlBDwTFXDSlDo7mnfvr2qLtIvCwlQPC2EzawCE5g2bZpImjRp4INs3KsN6J84caKNXjBrVQhQPFWpCfohLl68KG/dN23apCSN5cuXS/8w9I1GAhRPXgNKEciVK5fo0KGDUj5pzowYMUKKJ6Zk0kiA4slrQCkCQ4YMEdmzZ1fKJ80ZrP4EcaeRAAhQPHkdKEXg+++/l607vKtmJUqUELVq1VLNLfpjEwGKp03gma1/AokTJxYDBw70f4ANe7AKfLp06RyxgIkNeDyZJcXTk9WudqERsuKVV15RysmdO3fKFvG8efOU8ovO2EeA4mkfe+bshwBW/MeA+StXrvg5wvrNEE34xJlp1rNXNUeKp6o143G/IFRTpkxRhkLv3r3lGFQsgEwjARCgePI6UJJA7dq1RbVq1ZTxrV69eqJw4cLK+ENH7CdA8bS/DuiBDwKffPKJvE1WJVwKFmv+17/+5cNTbvIqAYqnV2te8XJjdSXcuiMapd12/vx5gdW4MEieRgIaAYqnRoLvyhEoWrSoaN68ue1+rV+/Xgo5w1XbXhVKOUDxVKo66Ex0ApMmTZJjK6Nvs+MzImWiFXz8+HE7smeeihKgeCpaMXRLCNwuQ7S2bdtmK46OHTuKzJkz2+oDM1ePAMVTvTqhR9EIQLTee++9aFus/1ipUiVRvnx56zNmjkoToHgqXT10rk+fPiJ//vy2gnj++edFp06dbPWBmatHgOKpXp3Qo2gE9u3bZ2t/o7YA8tSpU6N5xY8kwEHyvAYcQAD9nqNGjbLF02XLlknx/uqrr2zJn5mqS4AtT3Xrhp79P4EWLVrYFnRt6NCh4umnn1Zqnj0vDDUIUDzVqAd6EYDAhg0bZOvv5s2bAY4yZxdmFSFWO40EYhOgeMYmwv+VJIBb9zlz5ljuW7FixcQbb1DE1cMAAAnnSURBVLxheb7MUH0CFE/164geCiEwXAiLc1hpd+/eFalSpRL9+vWzMlvm5RACFE+HVJTX3Vy0aJHACvNW2q5du2R3weLFi63Mlnk5hADF0yEV5XU3sY4mbt3XrFljGYrZs2fLPPfv329ZnszIOQQons6pK897WqBAAdG+fXvLOPTo0UOkTZtWPHjwwLI8mZFzCFA8nVNXnvd0zJgxArN9rDIsyIyImTQS8EWA4umLCrcpSeDMmTPyNnrPnj2W+IdpoYjVTiMBXwQonr6ocJuyBPD0u3///qb7d+nSJRE/fnyB1i6NBHwRoHj6osJtyhLo1q2bKFKkiOn+aQPz165da3pezMCZBCiezqw3z3qN0L946n7u3DlTGYwbN07mg64CGgn4IkDx9EWF25QmAPHE6u5mGp7q58qVy8wsmLbDCVA8HV6BXnS/QYMG4vXXXze16K+99pqoWrWqqXkwcWcToHg6u/486T36IdH6fPjwoWnlz5Ili+jatavf9A8cOCAGDRokXxMmTBA3btzwe6y2Y+DAgVHnaOd+/PHH2m6+O4wAxdNhFUZ3/yIA8Vy6dKkpOBDoDenPmjXLZ/oY/5kyZUoZ2ROCmC1bNvHyyy8HFVCk+dJLL4myZctGvbp06eIzD25UnwDFU/06ooc+CJQqVUo0bdrUx57INyFWPIRux44dPhNDazF6SxOfIaAQ0kCGNH/66adAh3CfgwhQPB1UWXT1CQEsT5cmTZonGwz8hFvqZMmSievXr+tOFa3JQDHmsRI9xJPmHgKsTffUpadKgtYexGjz5s2Gl/utt94ShQsXDild3I4HanlSPEPC6YiDKZ6OqCY66YtAjhw5BAbNG20YhN+4cWPdyUIY0Qca6JZcE0/MkILoZ8+eXSC8SKBzdDvAA20hQPG0BTszNYLABx98IPLmzWtEUlFp4Al+8uTJ5VPxqI0BPuCpOwRRz1NzCCheEMwVK1bIh0Y4N3r/aYCsuEsxAhRPxSqE7ugncOLECdmKO3TokP6Tghy5d+9emSaiZgYziCDEL1BfZ6A0IJposY4fPz7QYdynKAGKp6IVQ7f0EUiUKJEYPny4voN1HDV37lwpnocPHw54NIQPw5PCFU4tcTxoCtRXqh3Hd/UIUDzVqxN6FAKBdu3aCQxbMsq6d+8uMED+8ePHfpM0SjiRDvo/9dzy+3WGO2wjQPG0DT0zNoLAzp07pQBdvXrViOREjRo1RPny5f2mpQlnnTp1xNatW+O8sB8GUUd/7KNHj+T/uDVfuXJlVLroK0UaeEqvnRO1kx8cQYDi6YhqopOBCKD15m82UKDzfO3LkyePeOedd3ztktu0p+bI09cL+2GVK1eW+y9fviz/h3iifzP6Objl59N2iceRfyiejqw2Oh2dQM2aNQ2JrX7t2jUpbkY8wEGL8+TJk9Hd5GeXEaB4uqxCvVic5cuXi4QJE0Zc9C1btkjx3LhxY8RpMQH3E6B4ur+OPVFC3A5H71MMp9ATJ04UCRIkEBcuXAjndJ7jMQIUT49VuFuLi+mUbdu2jah4rVu3FghvTCMBPQQonnoo8RjlCUyaNEkOMYrE0dKlS4u6detGkgTP9RABiqeHKtvNRdUe9nzzzTdhFzNDhgyiV69eYZ/PE71FgOLprfp2dWkzZswo+vbtG1YZT58+LR8WccB6WPg8eRLF05PV7s5Co9WIKZPhGB424aETonPSSEAPAYqnHko8xhEEjh49KgUQC4aEakOGDBHp0qUTt2/fDvVUHu9RAhRPj1a8W4uN1mM4g9wbNmwoSpYs6VYsLJcJBCieJkBlkvYRaNasmahUqVLIDmCOecuWLUM+jyd4lwDF07t178qSa3PPb926pbt8f/zxh0icOLEYOXKk7nN4IAlQPHkNuI4Abt0XLVqku1wHDx6UfaVY3Z1GAnoJUDz1kuJxjiFQoUIFgSBuem3hwoVSPBGvnUYCeglQPPWS4nGOIYBWJ8Jj6LUePXqI3Llz6z2cx5GAJEDx5IXgOgJYBR637hs2bNBVtqpVq4pq1arpOpYHkYBGgOKpkeC7qwjkz59fdOnSRVeZzAphrCtzHuRYAhRPx1YdHQ9EYPTo0QKrwgczLY7Q9OnTgx3K/SQQgwDFMwYO/uMWAleuXJG37vv37w9YpG3btsnjsBAyjQRCIUDxDIUWj3UUgRQpUoihQ4cG9HnKlCkiefLkAmJLI4FQCFA8Q6HFYx1FAH2eJUqUCOhz+/btRZEiRQIew50k4IsAxdMXFW5zBQFt8HugsBqI+R7KmFBXgGEhDCFA8TQEIxNRlQCGLM2YMcOve2nTphWDBw/2u587SMAfAYqnPzLc7goC9evXF7Vq1fJZlvPnz8uHRUuXLvW5nxtJIBABimcgOtzneAJr166VETF/++23OGXBPrRMgz2Rj3MiN5CAEILiycvA9QQgkIjtHtuwilLWrFnFgwcPYu/i/yQQlADFMygiHuB0Anji3qpVqzjFaNKkicAiIjQSCIcAxTMcajzHUQRmzZolMmXKFMfnQoUKiQ4dOsTZzg0koIcAxVMPJR7jaAIPHz6UfZvbt2+PUY5nnnlGTJgwIcY2/kMCeglQPPWS4nGOJpAtW7YYMdmPHDkiBXXdunWOLhedt48AxdM+9szZQgKDBg0SuE3XDMOT0PI8c+aMtonvJBASAYpnSLh4sFMJnDt3TrY0EZ4Y1qdPH1GwYEGnFod+K0CA4qlAJdAFawigpTl27FiZGQbO16tXz5qMmYsrCVA8XVmtLJQvAm3atIkamoQFkHv37u3rMG4jAV0EKJ66MPEgNxDYuXOnvHX/5Zdf5Pu8efPcUCyWwSYCFE+bwDNbewhgttGCBQukeO7atcseJ5irKwhQPF1RjSyEXgLFihUT+fLlE0mTJhWHDx/WexqPI4E4BCiecZBwg1sJYNV4tDy117PPPitOnTrl1uKyXCYToHiaDJjJq0MAAeE04dTee/XqpY6D9MRRBCiejqouOhsJgcSJE8cRz5YtW0aSJM/1MAGKp4cr32tFxypKWotTe//kk0+8hoHlNYgAxdMgkExGfQK3bt0SDRs2FPHixRPp06cXQ4YMUd9peqgsAYqnslVDx8wi8PjxY7OSZroeIkDx9FBls6gkQALGEaB4GseSKZEACXiIAMXTQ5XNopIACRhHgOJpHEumRAIk4CECFE8PVTaLSgIkYBwBiqdxLJkSCZCAhwhQPD1U2SwqCZCAcQQonsaxZEokQAIeIkDx9FBls6gkQALGEaB4GseSKZEACXiIAMXTQ5XNopIACRhHgOJpHEumRAIk4CECFE8PVTaLSgIkYBwBiqdxLJkSCZCAhwhQPD1U2SwqCZCAcQQonsaxZEokQAIeIkDx9FBls6gkQALGEfg/AYZWuoXX8fEAAAAASUVORK5CYII=[/img][br][br]What is the scale factor of the dilation that takes [math]P[/math] to [math]Q[/math]?[br]
What is the scale factor of the dilation that takes [math]Q[/math] to [math]P[/math]?[br]
What is our definition of similarity?
Triangle [math]DEF[/math] is formed by connecting the midpoints of the sides of triangle [math]ABC[/math]. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAV8AAADzCAYAAAAhHBWgAAAgAElEQVR4Ae2dCbiVU/vGv1JKpEFEUhkyJCkJZQypkCEalCGRkMhQhpQUUSgNUlJJyNBAUV+Iyt+UQoZKAyIlUyjiS63/9Vvf9x77bPucs/c+77zv57r2taf3XcO93n3v9T7rWffzLyMTAkJACAgB3xH4l+81qkIhIASEgBAwIl9dBEJACAiBABAQ+QYAuqoUAkJACIh8dQ0IASEgBAJAwBPy/eKLL8y8efPyHgH0S1UKASEgBEKNgCfke91115l//etf+R61atUyH3zwQajBUOOEgBAQAn4h4An5nnjiieaSSy7J6wMz4cMPP9xUrFgx7zO9EAJCQAjkMgKekC+z3gkTJuTDdejQoXYmnO9DvRECQkAI5CgCrpPv66+/bkk22cWAK6JChQo5CrO6LQSEgBDIj4Dr5Js8w4WE+/XrZwl5+vTp+WvXOyEgBIRAjiLgOvni601ebKtfv77B7ysTAkJACAiB/yLgOvnWrFnT3HHHHXn44oZgsQ0ClgkBISAEhMB/EXCVfDdu3JjSveD4gXmWCQEhIASEgHFX28Eh2WQXg/O5yFeXnBAQAkLgvwi4OvPF3YDbIdnwAyvSIRkVvRcCQiCXEXCVfM8++2zDTjaiG5wH7yFezXpz+TJT34WAEEhGwHXyZXeb8yC2l9AzfMEyISAEhIAQ+BsBV8n372L1SggIASEgBApDQORbGDr6TggIASHgEQIZke/XX39tZs+ebdavX+9Rc1SsEBACQiA3EEibfPv27Ztv59rAgQNzAyH1UggIASHgAQJpke/ChQvzEa+zfXjp0qUeNElFCgEhIATij0Ba5Dts2LCU5Dt+/Pj4I6QeCgEhIAQ8QCAt8p05c2ZK8q1ataqZMmWKB81SkUJACAiBeCOQFvkCQcuWLfMR8N57723atWuX99mAAQPijZR6JwSEgBBwEYG0yZc6cTN0797d9OnTx0C+gwcPNh9++KG54YYbTJUqVSwRd+jQwXz77bcuNlFFCQEhIATih0BG5JvY/XHjxlmynT9/vv34+++/N/fff7+pV6+e/bxBgwbaUpwImF4LASEgBBIQyJp8KaNnz56mfPny5o8//kgo0pjJkyfnuSnKli1rRo0ale97vRECQkAI5DoCxSLfLVu2mFatWplTTz01JY4LFiwwl19+uSldurSdDeOy2Lp1a8pj9aEQEAJCIJcQKBb5AhQ52mrXrm169+5dIG6rVq0ybNJA4YwY4VNOOcV89NFHBR6vL4SAEBACcUeg2OQLQE899ZQl1RkzZhSKFzPlMWPGmGOPPdYeX61aNfPMM88Ueo6+FAJCQAjEEQFXyBdgnO3HGzZsSAunF1980bRt29aSMLPhxLxvaRWgg4SAEBACEUbANfIFA8i0UaNGGcHx/vvvmx49epjKlStbIqaMtWvXZlSGDhYCQkAIRA0BV8l3+fLlNtTsmmuuyRgHZsz33XefOeywwywJ8/zKK69kXI5OEAJCQAhEAQFXyZcOP//886ZMmTJm0qRJWfcfH3Lz5s0tCVPW8OHDsy5LJwoBISAEwoiA6+RLJ++9915LnCtWrChWn+fNm2c6d+5sSpUqZcu76qqrDIt2MiEgBIRA1BHwhHwBpVOnTubAAw90BZ+VK1faLc1kRmZxjhxx+IplQkAICIGoIuAZ+X711VfmmGOOMRdddJFr2DDrffjhh03jxo0tCaOq9uSTT7pWvgoSAkJACPiFgGfkSwfmzJljKlasaEaOHOl6f4gpPv/88y0JMxsubJOH65WrQCEgBIRAMRHwlHxpmyPE/t577xWzqalPX7x4sSFFPSQPCbdu3dqsWbMm9cH6VAgIASEQEgQ8J1/6yUIZLgIvDRnLQYMGmUMPPdSS8CGHHGKTfXpZp8oWAkJACGSLgC/ki9xk06ZNzVlnnZVtOzM674knnjCnnXaaJeEdd9zRDBkyJKPzdbAQEAJCwGsEfCFfOvHGG2+Yvfbay9x9991e9ymv/Ndff91ceumlpmTJkpaIu3TpYjZt2pT3vV4IASEgBIJCwDfypYNjx461JPjqq6/62t/PPvvMLsjts88+tn6EfcjILBMCQkAIBIWAr+RLJ2+88UaDwPrmzZt97/Pvv/9uhd0JgWNxbo899jATJ070vR2qUAgIASHgO/lCuqeffrrdKBEk/C+88IKNjICEedx8881BNkd1CwEhkGMI+E6+4Lto0SKz3377mV69egUONyFwZNioUKGCJWEWBVevXh14u9QAISAE4o1AIOQLpEQkMOOcOnVqKBBev3691aSoU6eObddBBx1kZs6cGYq2qRFCQAjED4HAyBcob7/9dkt0YdPvffzxx21eOv4cEPUZPHhw/EZePRICQiBQBAIl3+3bt9stwvXr1w8UhIIqnzt3rrnkkktMiRIl7J8EYWsbN24s6HB9LgSEgBBIG4FAyZdWLl261NStW9d07do17Ub7fSCharfddpvZe++9LQkfffTR5q233vK7GapPCAiBGCEQOPmC5bRp06wA+/jx40MNLaFqiAQdddRRloR33313M27cuFC3WY0TAkIgnAiEgnyBhp1v+Fg//fTTcCKV1Krp06ebc88917aZdhO/LBMCQkAIpItAaMiXBqP9u++++6bb9lAcx065bt26mfLly1siJoYZN4VMCAgBIVAYAqEi3y+++MJmP27fvn1hbQ7ld4SqDRw40Bx88MGWhGvXrm2YHcuEgBAQAqkQCBX50sDZs2dbbd6hQ4emam8kPmPL8imnnGJJeIcddrCkHImGq5FCQAj4hkDoyJeeQ7z4UaMeUYCAEK4U+sKD18hryoSAEBACoSRfhoXQs8qVK8dihJYvX25uueUWU61aNUvCREssWLAgFn1TJ4SAEMgOgdCS74YNG6z4TsuWLbPrWQjP+u2338yIESOsX5uZcJUqVcyYMWNC2FI1SQgIAa8RCC350vH58+dbAfZ+/fp5jYPv5aNpcfbZZ+e5JMhDx44/mRAQArmBQKjJlyEYPXq0JSgW4uJo7777rrn66qvNLrvsYvvZvHnzyMQ6x3E81Cch4BcCoSdfgOjRo4chauDnn3/2Cxff61m3bp3daHLggQdaEj7ggAPMc88953s7VKEQEAL+IBAJ8v31119NixYtTJMmTfxBJeBaJkyYYBOO4hcm/1z//v0DbpGqFwJCwG0EIkG+dJqdZAiwX3/99W5jENryXn75ZXPhhRfm+YUvuOACw2YOmRAQAtFHIDLkC9To7DIbfPrpp6OPfAY9WLZsmc36seeee9r+N2rUyLz22msZlKBDhYAQCBsCkSJfwEPaEQJes2ZN2LD0vD3kvxs2bJhp2LChxWC33XYzDz30kOf1qgIhIATcRyBy5PvXX3/ZxJeHHnqo+2hEqMQpU6YY8s3xR8TjmmuuMf/5z38i1AM1VQjkNgKRI1+G6+OPPzaQb+fOnXN79IwxhKpdeeWVply5cpaEmzVrZpYsWZLzuAgAIRB2BCJJvoBKGNaOO+6oHWL/u8IIVRswYIBBTY2Z8P77728mT54c9utP7RMCOYtAZMmXEYNsIBrN9PJfv2QEOemkkyw25J/r27dv/gP0TggIgcARiDT5gl7Hjh1N9erVAwcyjA0gVK1Dhw6WhPmTatu2rfn666/D2FS1SQjkHAKRJ9/Vq1ebI4880px33nk5N3jpdphQtZ49e5qqVataIgYviFkmBIRAcAhEnnyB7qWXXjIVKlQwgwcPDg7JCNRMqNqDDz5oGjRoYEkYyU5C16Js7AZEeCn5QVYUmRAIMwKxIF8AfuCBByyhoIQmKxoBFizPPPPMPJcEERNkZ46aHX744aZmzZpWfvTEE0/Mexb5Rm0kc6+9sSFfhq5Lly42kSWxwLL0EHjnnXescP1OO+1kifjUU081ixcvTu/kgI/auHGjbbNy5QU8EKo+KwRiRb6EWx1//PEGApFlhsA333xj7rzzThuixuIcOhpPPPFEZoX4fPTrr79uyVezXJ+BV3WuIBAr8gURNA/QQOjdu7crAOViIY8++qg54YQT8lwSbOkOo91xxx3W1x/GtqlNQqAoBGJHvnR41KhRljhmzJhRVP/1fSEIzJkzx6CkxkyYR5s2bUyYZplkAqlVq9Y/FtsK6ZK+EgKhQSCW5Au61157rSWMH3/8MTRgR7UhS5cuNTfeeKPZfffdLaYI+8yaNSvw7rDQlrzYRjommRCIAgKxJV+yXpx22mk2WWUUBiIKbdy0aZMZMmSIqV+/viXhSpUq2SiTINrODJzZOH5fmRCIIgKxJV8Gg5V8Fo5Q/JK5i8Czzz5rzjjjDEuAkCCRJmQc8cuIcKBeIh5kQiCKCMSafBmQxx57zP5IJ02aFMXxCX2b3377bUu8ZcqUsTifcsopVmnN64az2IbLQSYEoopA7MmXgbn55pstMbAVWeYNAmvXrrULX9xpMCPdd9997R+fN7UZu5nikksu8ap4lSsEPEcgJ8j3zz//NKyMH3TQQZ4DqgqMGTt2rDnuuOMsCUPEvXr1ch0WtpMT6YB6W+LD9YpUoBDwCIGcIF+wQ3YSAfaLL77YIyhVbDIChKq1a9cuj4TPP/98s2rVquTDMn6Pnxe3Q/IDnQeZEIgKAjlDvgzIM888YwXYlffM38uTULUbbrjBVKlSxRLxEUccYRSD7e8YqLbwIZBT5Av8bKHlVjgq+gXhu2SybxGhaggg1atXz44BroNBgwZlX6DOFAIRRiDnyJexYtcWW5BlwSFAqFrLli3zXBKXX365+emnn2yDvvvuO0vKbJiQaE5wY6SavUUgJ8l35cqVVoCdRbhctQ8++MA8//zzVt933rx5gcFAqBrEW7p0aUvExx57bJ7oO3coPG655ZbA2qeKhYBXCOQk+QImPkduewcOHOgVtqEsl8WqTp06WVJz9G/BgYiBIDcsEKpGrrmKFSvmzYYd8uX5l19+CSWeapQQyBaBnCVfACPzBT9slNByxSBYbucTBXKYBUPAQ4cODRyG008/PSX5fvzxx4G3TQ0QAm4ikNPkC5CdO3c2CIkTC5zL5syCg8KANPe4HBJnu8mvydO3fPnyoJqoeoWAqwjkPPlyu4sAO7fduWyQr987xn744Qe7K84JQSPTMrHBxGI7xIsv+OijjzY9evQw5Jzjc4R9pk2blsvDpb7HAIGcJ1/G8NVXX7XRD2xDzkXzWyHszTffzNMJrl69uhW+X7FiRT7oeb9gwQLDc9myZa2aGsI9999/vznssMMsCe+6667m7rvvznee3giBqCAg8v3fSI0cOdL+oHNxRkUSSj8iP8aPH2/YYMHsle3HbEPeunVrkb8VwtI4Z+7cuXnHsmGmefPm9nO+u+yyywwhajIhEBUERL4JI4X0JD/kDRs2JHwa75e4GiBfryIdvv76aytsxIIe2F500UX2TiNTVAk323///Q2uikR76623rN++VKlStvymTZsaZbBOREivw4qAyDdhZAjyR4C9QYMGCZ/G96WXxIsr55xzzrGEWKNGDRtGVlxVOcamdevWKQcEku/Tp4+VmYTkkZscPXp0ymP1oRAIAwIi36RRwB+JHOKVV16Z9E283npFvOhmIGAEAbKIidjN9u3bXQFv/fr1ZrfddrNbxAsr8JFHHjGNGze2baAdN910k9m2bVthp+g7IeA7AiLfFJCPGzfO/nDjqpLlNvGyKEbOvHLlylncLr30UuPVrrmXXnrJ1sHuvKJs9uzZBiU1CJgHs+ZPPvmkqNP0vRDwBQGRbwEw9+zZ0/5gk1fhCzg8Mh+zkQIiIlwrUQfXec2Gi3Rt5syZpkWLFrY8tHX79+9v1qxZk+7pWR83YMAAs8cee5gvv/wyrTIgXDaWOLvn8HGziCcTAkEiIPItAP0tW7bYCAAyM8TJSDiZrIOb+D5x51uqfrMZhXCvAw880JIuaYOCSNF07rnnmmbNmqVqYoGfOaFqjlukfPny5q677irweH0hBLxEQORbCLrMAuvUqWNjUgs5LCe++uijj8wVV1yRJ4BDwsz/+7//C6zvmzdvtotq3KFkY4SqsYDnuCTY6bhu3bpsitI5QiArBES+RcDGttcdd9zRqn8VcWgsv37uuecMs1tIilAvhIi++eabUPQVvzLteuKJJ7JuD6Fq+KhLlixpy8L9khhPnHXBOlEIFIGAyLcIgPia23J+5AsXLkzj6Ogf8vPPP9vbcaI+6DczRP6EwmhDhgyxC33FFd5xQtX22Wcf22fC45TxJIwjHp82iXzTHMv27dvbMKc0D4/kYe+++67Vd4BwmQkSbvfOO++Evi8XXnihDS3766+/XGkroWrHHHOMJWGwuPHGG3NeeMkVYFVIPgREvvngKPgNaloNGzY0SB7GzR5//HErLgTR1K5d20ptRm2XH755t2OzCVUjPA1ceLBp5MMPP4zb8Ks/ASEg8s0AeGJL2SZLHrioGxsWevfubRC2gVgIGYty+NV7771n+/Hwww+7PjSEqhHH7GyRJgfdU0895Xo9KjC3EBD5Zjje9957r/2Rv/zyyxmeGY7DWaRCuhHCRa6xW7duBuKKg40ZM8b2i0U0L4xsGvfdd5+NgAG/XXbZxRBzLBMC2SAg8s0CNVbHEXL57bffsjg7mFMgJsePedBBB9kswskiNcG0zN1au3btaurWrWtYNPTSnn76aXPqqadasoeIuSa++uorL6tU2TFDQOSbxYDyI0MSkcwLYbbPP//c9OrVKy8hJf7qXJDMbNSokenYsaMvQ4MWCNu1S5QoYYkYUXoE4WVCoCgERL5FIVTA97gdSD9/ww03FHBEcB+zUNSmTRtLBmXKlDHdu3c3mWwbDq7l7tS8bNkys8MOO1gXgTslFl0Kf8i333672XvvvS3uhKyhES0TAgUhIPItCJk0Ph82bJj9obERIWgjzGrEiBE2IoPbYFb/H3zwQc9vv4Pud0H1s/ECHILwzePiOeqoo2z9tOH666+PlIuqIEz1ubsIiHyLiefVV19tf2RBbU399NNP7Y/byW/WqlUrM2PGjGL2Kh6nc1eC4A95+oKwWbNmGTQoIGAeZAtZtGhREE1RnSFEQORbzEH5/vvv7Q4wFnn8tOnTp+eJlZN9GdWu4u7y8rP9ftXFdmE/UiQV1h/GBdcPQj6QMDnoirMlurC69F10EBD5ujBWb7zxhhVgJ4+Yl7Zp0yabSJI4U37EEP7w4cMNIjOy1Agw6yXRZt++fVMf4OOnRGAMHjzYHHzwwXb8dt55ZyvD6WMTVFWIEBD5ujQYJIOEEHl227hVJb+cM3NiJoeouCw9BLhLYGymTp2a3gk+HIVWhiNYRNs6depkiE6R5Q4CIl8XxxoNAH5IS5cudaVUdpydccYZtkwC+vFhspIvyxwB8ruRgihs+CHLefHFF9sx5to54YQT9Mea+fBG8gyRbwbDhtB4v3798j0SQ7jYdMGslDCjbI305+yiO+SQQ+wPEhcDIUt//PFHtkXqvP8hwB/ZySefHEo8nFC1atWq2XFn2zfRK7L4IiDyzWBsyenG7IRAeh6ko+E9gitO6vXFixfbMC9yh2VibIlld1bZsmVtmaySE68rcw8BMlnstddeoYzNTuwloWpsFOHa4tGjRw/D1mZZvBAQ+WYwnkQUQLiJ5vgT+c4xVrIRYCfdTlH25JNP2nQ4/MhYGCLTbtzyxhWFgZ/fv/LKK5bQJk6c6Ge1WdVFqBp/7A4Jn3XWWZGQ+Myqszl4ksg3g0FntstW0mTjM5IzJhq7nfjR3HPPPea2224zpK1xDOFuBFkOOOAAe0yDBg0Malxbt251DtGzhwjg1mHnX1QEhZxQNfz+XFNEuQSRN8/DIcnJokW+GQw7Fz7Zf5PNcUck+n+3b99uA/ydWQvP6EGQK4ytr7w/77zzpAOQDKZP79u2bWt3oRG+FxVzQtWc5KXlypWLhbxpVPB3u50i3zQRhVghzESCdU4lI3Dyd/hw+Sz5QWwnYjerVq1yTtdzQAhw50Ei0CgaoWpNmzbNu764+5K7KlojKfJNc7yY8UKkqSzVd85sOJl8H3jggVRF6LMAECBFEuMTZQGc5FC1448/3rz44osBoKkqM0UgNZtkWkoOHM/MAp9vKuO7mjVr5vuK7AfJxMv7SpUqWfUrab/mgyuwN4RzMS7cvUTZ1qxZYzOToLRHfwhZQ/hJFl4ERL5pjg1RDokRDc5pxP6y2JbqOyfrcSIJDxo0yNSvX9/+QCBt9GBlwSKAEDpx1UGJI7nZe9YaRo8enadux7XHtfnjjz+6WY3KcgEBkW+aIHIRE1aWaMT2ItxCbi8nzjfxe17j20VykhAnFtyQGsT4zNm9hu8urKnZk/sT1/f8uZKhOk7GFnQ2/Th//ije4aaQhQMBkW8a4+AsqDHLdQwiZgYL8aZahHOOS3xm0wS3hShcOcbC3BVXXGHzqbEAhPCK1ylwnLr1/DcCSHNCUoShxc0++ugjqw1CdAR9PPTQQw0Zq2XBIiDyTQN/x33ALNdxGXAR4zZIJOQ0irKhapybPNPFB0xW5H333dfGoELQkohMB1H3jhk/frwlp5kzZ7pXaIhK4u4Mt1ft2rVtP5EiZbu8LBgERL5p4A7BMvtNfBTkZkijOOMIsBe06Pboo49aFwUkzQ4ndjrJ/EEA9Ti0OeIetvXUU09ZlxnXGA/EfcImOuTPiAdXi8g3AOw3bNhgtxSTRbgww03Rrl07++No2LChYc8/6YJk3iLQpEkTc+aZZ3pbSUhKR4v6oosustcYJExSWGVC8WdwRL7+4PyPWubPn29dDMw4ijLcD8hJkipo9913tyFFhBbJvEGA7d8IHPXu3dubCkJY6pdffmm3wVetWtUSMQJE5ACUeYeAyNc7bIssmZkssw1Cg9IxFuLYpEEaGudWUavX6SCX+TFEo4Bxsm8+85Kidca2bduszgh6I/Sfx7XXXmu4W5O5i4DI1108My7NEWDPdHHt6aefNi1atLA/DoWqZQx7WifcfPPNNob7/fffT+v4uB2UHKqGKwY3hcwdBES+7uCYdSlozCIVSAhaNsbMl9xxiPU4oWo//fRTNkXpnBQINGvWzO5s/P3331N8W/hHLNDOmzfPPoqzQFt4Ld5/64SqER3BTLhOnTomCpKc3iNTvBpEvsXDz5WzFy5caC/o4mTZxWdHksgaNWooVM2VUflvIbh6SD+UagdjQdUQmsiuR2LA2ZLOM++TN+kUdH5YP3dC1fbff39LwvjF6asWgbMbMZFvdri5fhZB7wiwuxHkjy+5cePG9geiZJvFH6o5c+ZYLB955JG0CoOQmPUmGjHhyZrPid9H7XVyqBoRE5m6zqLWZ7fbK/J1G9FilOcIsLvlV8NnRzojbhWPOOIIu7D3n//8pxgtzN1T+/fvb0qVKmUWLFiQFQiQMeOQ7m7IrCoJ4KTkUDXC9F544YUAWhK9KkW+IRozbt+I62UbKAIpbtmSJUvsbTO3v06oWqY789xqS5TLYcML8dbZrPw7EqNR9v0WNnZOqBrXF38yrGGkSjxQWBm59p3IN2QjjhQlP3AiGNw2kjCiHcGCCT8QYowVqpY+yoRh4VMnG0m6xp/cY489Zl0OuCPibqlC1dgq/80338Su68X9IxX5hvCSmDJlil2kueWWWzxrHT47VvIhYYWqpQ+zk6FkyJAhhZ7kuBnAl0cuaigg6k4kj4MBKn7Zum0KBdvHLxlXNF6cPvFcq1atjDVeaLLI18eBy6Squ+++2w6w1yIv7LTr1KmTrYtVbIRXvv/++0yamnPHOplLCtPcYFbED5UHLgckKxFlKu5sKYpg4/bq1q2bjcKBrNBO5m4gaua4jlg8ZVzx3/Oc7R2NyDfEVwAi31ysfsTtOpkQ9t57bxt1gcDMhx9+GGJ0gm1ax44dDYksV69enVZDIF3GMpf9oFzHRPPst99+FgsySBMe+ccff6SFYZAHQbKMHwTslol83ULSg3L4YSPATqSCn0Yae0TfudgUqlYw8szg2rRpU/ABSd+QairbWVJSUZF/++STT9oYaK4xHvyZsZkjrMbYFZRGLNs2i3yzRc6n8wgXY+X4qquu8qnGv6tB3ercc8+1Pw4nVG3Lli1/H5Djr4hrhTgIQyvKuEXl2KhvtCiqn5l+jw/4wgsvtNiAD/Hpzz//fKbFeHo8Y0bb3A4TFPl6OmzuFM7iDoP/xBNPuFNghqU420t32WWXvFA10iPJjEF7mbF59tlnLRzcnuLbZYENEuHRo0cPG+3g9swpTvgTFXLrrbeaKlWqWDxRVytqUdOv/rO7MTlBrht1i3zdQNGHMhwB9iDjc9GhwGeHDjGEw64mFuxy3UgDRbZgFpbw7eLXhWgTH276CuOMN7Huo0aNypcxhvUHZD6DMmcc3a5f5Os2oh6Vt379ehsaRkRCGGzSpEnm5JNPtiRM6A2ha7lsRx55pGnZsmUkFo+iMk5E+pD0kz96Hqeffnogf/Yi36hcMR6287XXXrMC7B06dPCwlsyKxmfnZEJwQtWy2QGWWa3hO5pokZIlS5pevXqFr3ERbxFRN9z5lS5d2pLwwQcf7GrUQVHwsOgMAbttmvm6jajH5RGJwCxg5MiRHteUWfHko8Nnx+IgAkHcKi5evDizQiJ+NH5fxmbcuHER70k4m//jjz+ae+65x05AwJnrDD2UzZs3e9pgJ64bf76bJvJ1E02fynIE2N1efXWr+fwxsEWaHwizhlzKCUa6p/Lly5s333zTLThVTgoEkkPVuBvE5+6VseCGKh2bQxyNZtIsFWcNRuTr1Wh5WC4as2zbZGU4zIbPztleSloaZu2//fZbmJvsStu4RSU++4cffnClPBVSMALJoWrHHHOMJ+F8LKSysw1xKiYVPNi1KPIteGxi+80777xjBXLYLx92Ix4Wnx2ZEPjDuO2222Kdmp2dXMx+6bPMHwScUDWE7yHGPfbYw+Y79Kf27GrRzDc73EJxFrdALEKgAxEFI1SNtiQN1DgAABEqSURBVJLuiB8IC3Vu+9HCgsPs2bNtH4cNGxaWJuVEO1KFqqErwZpE2EzkG7YRybA9jgB71EiMUDVuzyFhQtWC2kCSIdwZHc5GixIlShgyYcj8RyA5VI1QQPy1YTGRb1hGIst2/Pnnn1aAnRlwFLNUkAmBxRJImFA1NnGsW7cuSzTCdxqxqex4Q2xcFgwCTqgamUi4ztgkNH78eNuY++67z9SrV88qrfkt+ynyDeZ6cLVWVnmJLmCRJ6rGDiZiZMmE4ISqvffee1HtTl67uQ0m/A7helmwCCSHqhGXDRknPliP8MtEvn4h7XE9zzzzjNl1111Nz549Pa7J++JHjBiRt72UaImwCa1kigDZQviBR8U3n2n/ong8bi4WRROJl9f77LOPb90R+foGtfcVOQLsUScrByl8dkRz8KMgVO2hhx4yLNpF0R544AHbj6lTp0ax+bFr88SJE83OO+/8D/JFo8MvE/n6hbRP9ThZKeKUjYJQta5du1p3hBOqtmzZMp8Qda+atm3bWr82efpk/iOAa6tPnz4GxTT+0HFvJc98b7rpJt8aJvL1DWp/Klq5cqX1/R522GH+VOhjLZs2bTJ33XVX3vZSQtVeffVVH1tQ/KpYVEQjeevWrcUvTCWkhQCRQBdccEEe0SKChJsOY5Ft3333NdWrV/fdZSfyTWv4onUQt+v8u3fp0iVaDc+gtfjsWGBk5kKoGreRUTC0kWkzOhgybxFAa9nJyALmiLaHKVuGyNfb8Q+sdEeAPYqJCjMBjcWs9u3bW0IjN9jAgQPN2rVrMynC92MfeeQR2964j43vwBpjPv/8c0PW78qVK1uM0WNgLSSMYZgi3yCuEJ/qJPUQ//i4IqJq3DKms38ewsVfx4+OmGd2NbEFO6x22WWX2buTMLcxrNilatfLL79szj//fHu9c82j8TBt2rRUh4bmM5FvaIbC/YZASM2aNTM1atRwv3AfSnSk/DJNOomqGj5vfoSEqoU1woDgfsYnF9PJu3X5INZEJAxjzYOM30uXLnWreE/LEfl6Cm/whbMgxYICK+1RMuQyuWUsTsbfF1980WaX4EfJD3T48OEGRbiwGDN62ta9e/ewNCkS7fjss88MsqpOnC4iOoMGDYpE2xMbKfJNRCOmrx0B9iiJvCDXx4wX/YdMZ77Jw0hoF4uPO+ywg1VVu/nmm82nn36afFgg759++mlLwGETxw8EjCIqJZM3+tDOLPf444+PtFa0yLeIAY/L14h8c9EuWrQo9F2CbCFfzA3ydTpMxgMWX3DDgAWr3/gKg7brr7/elCtXLnJhc37gtm3bNnvHUrdu3TzS5Y80yusYDm4iXweJmD+jMYv/EzHoMBsLbLTRWWRzk3wT+00mhCZNmtgfNHUgtIIOQ1DWuHFjwyPILL1B9T1VvdytXHvttaZs2bJ2jIjDDUsq+VTtzeYzkW82qEX0nLfeessKsJ922mmh7AELT7Vq1bKp150GekW+Tvmk+2nTpo39gROqNmDAAEMyTL+NrBdlypSxC0Z+1x2m+tgajxKc41po2rSpmTVrVpia6FpbRL6uQRmNghwB9jvvvDN0DSZNCz69RPOafJ26vvnmG7vDiVk3oWpXXnml4c/KT8OnCekgq5lLhiwq2hdIPdJ/8CcLiHP3E1csRL5xHdlC+uUIsIdpa+706dPtD4+Zj5OgkGe0cNGr4LVfIVkI+Bx66KG2Pa1atTLPPfdcIWi6+1Xfvn1tveARd0Nnl1h0FkIhXbZeE5GSKybyzZWRTujnli1brAA7Fzyvw2AsstGewh5+Z+tgJoqLhjbxJ0C2WjRhvbbmzZvbOOUoigelgw1/ZsQ3O2PN61deeSWdU2N1jMg3VsOZfmeIo0WA/eijj07/pACO9MvtUFjXCEtjhR2yIEEjmsleagSwFZadeuzY2r59e2FNi8x3v//+u7nnnnvyRJGQc2RBLZcXGEW+kbl83W+oI8BOqFNYLQzk62BD2ntC1Vh5h4hRyiJRphdGeiXqwEUUZSO08fLLL8+b5R5yyCGGuHOZMSLfHL8KHAH2KVOmhBKJ6667zkyYMCF0bSNUjbsGCPKEE04wKGi5Ld5CfjHKJ9lo1Oypp56yanO0nwcRDH67jcKOmcg37CPkQ/scAfb169f7UFu8qiBUja3bEAyhakSRoKzlluF6IPwuCvnsyDLSv3//vDuDSpUqGTb3fPvtt27BEatyRL6xGs7sOrN8+XKrjXvwwQdnV4DOMoSqkQAUvQGy5F5xxRUG14EbRl6xFi1ahDaFEspshAk6s1wWJ8eOHetG12Ndhsg31sObfudmzJhhJQ47d+6c/kk6MiUCo0aNMvyRQUbkoEO/oThGSBZl9ejRozjFuH4uAvbHHntsHumygxJ9ZVl6CIh808MpJ45yBNjHjRuXE/31upPszEoMVWMjQba59caMGWNJLujFKrapJ+ZB23PPPQ1CRezQk2WGgMg3M7xif7QjwI4rQuYOAujL4oZg9kqoGn5QZrOZGlq1JBANYuGKGW2HDh3yZrmk5wnjQmimmAZ5vMg3SPRDWPdXX31lA+D32muvELYu2k0i1pU0R2ALEbdr186wkSMTq1OnjvXPr1u3LpPTsj42OQ8aC4DKvpE1nPlOFPnmg0NvQIDdRqywt27dWoB4hAChWE6oGolAcSuks9tw9erVlrhJQ+SVfffdd/nyoCHB2bt3b/PLL794VWVOlivyzclhL7rTjgA7fkqZdwgg3sMMmJkwGUfQdli1alWhFULcHE8csJs2f/78PIU3yudPgSzRMm8QEPl6g2ssSnUE2HWb6f1w4kZg4QpRdULVmNlChgUZm0+QoCRKpbjGH62TB40yO3bsGAnR/eL2O+jzRb5Bj0CI62dlnvAhCEHmHwKQoSOvSHwvM91URoZeYmpXrFiR6utCP2NDTWIetNq1a5t+/foZtlDL/EFA5OsPzpGthVVu9uOfcsopke1DVBuObgQKZ7gAyMaMmyFxtxh/jiVKlLBui3T7OHfuXHPOOefYMimXcS1uHHK6deu4/AiIfPPjoXcpEHAE2PFHyvxHAGnJrl27WsJE7YzNFosXL7YNmTlzpv28qCSjI0aMME4eNHbhEba2ZMkS/zujGvMQEPnmQaEXhSHAajczpX//+9+FHabvPESAaAhkGdnYwFgQ9oXP1xHHb9SokU08iq+esDbkGhPzoCEQf9dddxkyR8iCR0DkG/wYRKIF+AKdVflNmzZFos1xbuTkyZMNPl9ImEzPPCc+dt9997z3LVu2NFOnTo0zHJHsm8g3ksMWTKO51T3iiCOsCHswLVCtyQi8/fbbeSmPEsmX16itIQQvCycCIt9wjktoW+UIsHM7KwseAZJMEvGQTLy8d/zCwbdSLUiFgMg3FSr6rFAE8Bvy44aIZcEgkJhfLhXx1qtXL5iGqda0ERD5pg2VDnQQIK+YI8C+du1a52M9+4DA/fffb0XbIdxq1arZBTXifEePHm0OOOAA+6eIkpqXOeZ86GZOVCHyzYlhdr+TKHWx/ZQfvMxbBFauXJkvDxoLbQVt+3Y7lZG3Pcvt0kW+uT3+xeq9I8B+8cUXF6scnZwaAfBt2rSpnc2WLFnSLqChESyLBwIi33iMY2C9YAbGLTCqXDJ3ELj33nsNqYPAFXW5m266ydW8cO60UqUUFwGRb3ER1PnGEWD/5JNPhEaWCCBen5gHjYzIw4cPz7K0wk87++yzLbEnL9RNnz698BP1rasIiHxdhTM3C/vyyy+tADuB/bLMEJg2bZr1nUOEZcuWNRdeeKF5+eWXMyskw6Nr1qxpiZ6MGImPjRs3ZliSDi8OAiLf4qCnc/MQcATYmVXJCkeAaBHC9ZxtwiiYsX2b7cBeGwQL0WuW6zXSRZcv8i0aIx2RJgKOAPvgwYPTPCO3DsMtk5gHrVmzZr77ypnpQr6a5QZ/7Yl8gx+DWLXAEWB/8803Y9Wv4nTm2WefNSSchPQqVKhghdJfe+214hSZ9bmon+F2kAWPgMg3+DGIVQs2bNhgBdh33HHHWPUr084Qb4s4OdmKIV30eO+8806DiHmQduKJJ9rtyPPmzTOJjyDblKt1i3xzdeQ97LcjwM4PPdeMlPAI2kC4PM4444xQpVhn5u20zXnOxXEKw3Up8g3DKMSwDY4A+2233RbD3v2zS6T6cfKgEfVB+N0bb7zxzwMD/AQRHggXv68seAREvsGPQWxb4AiwIwITR0OwvE+fPmbXXXe1pNawYUMrdk56nzAaEQ6QrxbbwjE6It9wjEMsW4HouiPA/vPPP8emj4sWLTLnnXde3u1769atzZNPPhn6/pHxGOF1WTgQEPmGYxxi2wpHgD0OP/pJkybl5UGrXr26zaWGmHlUDN8uu+hk4UBA5BuOcYh1KxwB9quvvjpy/fz111/NrbfeanbaaSc7023SpIkZMmSIieJMHpfD0KFDIzcGcW2wyDeuIxuyfjkC7FG4PQe6d9991zgaCKVKlTLt27c3U6ZMCRmqak6UERD5Rnn0ItT2v/76K0+AHS2IsNqECRMM232ZJe63336mV69eBh+vTAi4jYDI121EVV6BCCDAfuyxx1qZxAIPCuALVv979uxpmOFCuieddJIZOXKk2bx5cwCtUZW5goDIN1dGOiT9dATYO3bsGHiL2ALNJggIt1y5cgZReNonEwJ+ICDy9QNl1ZEPAUeAfdSoUfk+9+vN2LFj8/KgHXLIIeb222837EyTCQE/ERD5+om26spDwBFgX7JkSd5nXr5g48P1119vZ7nMdJs3b24g4T///NPLalW2ECgQAZFvgdDoCy8RYKvrqaeeaipWrOhlNWb+/PmWaCHcSpUqmS5dupg5c+Z4WqcKFwLpICDyTQclHeMJAo4AO35Xtw1t4Ro1atiZLhs8BgwYYJYtW+Z2NSpPCGSNgMg3a+h0ohsI4PdlVjpw4MBiF4dcY/fu3fNcC61atTITJ04027ZtK3bZKkAIuI2AyNdtRFVeoQgQ1kUoF/G0jjkC7LgIsrG5c+daFwYkXrVqVdOtWzcpd2UDpM7xFQGRr69wqzLEXSDJxFxv3377rWGWWqJECcNmjHSNWNxq1arZ8ho1amQGDRpkVq9ene7pOk4IBIqAyDdQ+HOrckdPFuJNFvB2BNiPO+64QkEhySQaERA4D9TFJk+eXOg5+lIIhBEBkW8YRyWmbUJRC9JF3CVVlAOuiNKlS5vGjRvb4yDZFStWWDRIp467AsJlIQ1XhfLExfRCyZFuiXxzZKCD7qaTNZdn53WqNpHc0ZnV8kzaGzJD8JpZ8YMPPmjWrl2b6lR9JgQihYDIN1LDFd3GJmrJOuT7wQcf5OsQM9lE4nVe48+dNm1avmP1RghEHQGRb9RHMALtd8gWn69jECufJ9qsWbNSkq8bYWiJ9ei1EAgDAiLfMIxCzNuQ7EpwZrTJwt5btmwxlStX/gcBL1y4MOYIqXu5iIDINxdH3cc+s4iG35bkjcx0nQe7zu64445/tITZb926dS0BE0YWlPjOPxqmD4SAywiIfF0GVMX9jQAbKmrVqpWSZPEBJ8b6/n3Wf1+xW00mBOKMgMg3zqMbcN+Y2TLrTZWqnO+SY30Dbq6qFwK+IiDy9RXu3KkMwiWWN5VrART4PFWsb+4gpJ7mOgIi31y/AjzqP+SLfzfVrJcqiXxIjnbwqCkqVgiEEgGRbyiHRY0SAkIg7giIfOM+wuqfEBACoURA5BvKYVGjhIAQiDsCIt+4j7D6JwSEQCgREPmGcljUKCEgBOKOgMg37iOs/gkBIRBKBES+oRwWNUoICIG4IyDyjfsIq39CQAiEEgGRbyiHRY0SAkIg7giIfOM+wuqfEBACoURA5BvKYVGjhIAQiDsC/w/lQU/HJ6TGWQAAAABJRU5ErkJggg==[/img][br][br]The lengths of the sides of [math]DEF[/math] are shown. What is the length of [math]BC[/math]?
If [math]AB[/math] is 12, what is the length of [math]A'B'[/math]? [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUIAAAFGCAYAAAAfPJaKAAAgAElEQVR4Ae2dCdhNVfvGP5lDZKZkSOIvyZRkShlKmWXKGGXOPPWZMpTMhEJkihAyJWPmMUSGDJkiIWTKFOt/3auW77znPec9+5yz532v63qv95y9117Db+19n7XX8Dz/EQwkQAIk4HEC//F4/Vl9EiABEhAUQt4EJEACnidAIfT8LUAAJEACFELeAyRAAp4nQCH0/C1AACRAAhRC3gMkQAKeJxC1EH7xxReib9++Mf6OHz/uebAEQAIk4BwCUQthypQpRenSpUWfPn1Eu3btRP78+cV//vMfsWDBAudQYElJgAQ8TSAqIUTPD6L3/fffx4AIMYQ4MpAACZCAEwhEJYTo9UEIL1++HKOujRo1ohDGIMIvJEACdiYQlRDidThr1qwx6odeYqpUqeSrcowT/EICJEACNiUQlRDi9TdbtmwPJkqqVq0qhRFjhQwkQAIk4BQCUQkhXovVeCBEEb3Dl156Sezevdsp9Wc5SYAESCDyvcYQu0ATJVWqVJG9RLIlARIgAacQiLhHiPWDEEL/MGLEiIDH/ePxOwmQAAnYhUBsJdNYMowDBloig+NYW8hAAiRAAk4hELEQYmzQf1JE9RIxm8xAAiRAAk4hELEQ4rXY/w89QYqgU5qe5SQBElAEIhJCLKDGbhLfP+4vVkj5nwRIwGkEIhJCp1WS5SUBEiCBuAhQCOOiw3MkQAKeIBBQCHfs2CGaNWsmypcvL4YMGeIJEKwkCZCAdwnEEsKffvpJJEiQIMZECIwoMJAACZCAWwnEEsKuXbvGEEE1M3zmzBm3MmC9SIAEPE4glhDilViJn+//LVu2eBwVq08CJOBWArGEcO7cubGEMHHixPJYixYtxMmTJ93KgvUiARLwKIFYQggO8EGSPHnyB4KICZNx48Y9MMNfv359ceDAAY8iY7VJgATcRiCgEKpKYvYYr8ewKKPClClTRLFixeRx2B/cvn27OsX/JEACJOBIAnEKIWpUs2ZNKXpr166NUUG8QpctW1aew/81a9bEOG/1F+x+QZn93QhYXS7mTwIkYD8CIYVw27ZtUuyaNGkSsPRLly6VPUb0HNFTXLRoUcB4Zh2EH5XnnntOlllN9sCKNo3FmtUCzIcEnEcgpBCiSjC3FS9ePLF3796gNUTvq27dulKA8uXLJ2bOnBk0rpEnsOYRhh/U3mf0CPFqDz8qDCRAAiQQiIAmIVyyZIkUuI4dOwZKI8YxtSsFvbHs2bOLCRMmxDhvxZdg1rStKAvzJAESsB8BTUKIYufJk0ekSZNGnD59WlMt9u/fL9577z2RJEkSkS5dOgHL1X///bema/WOpNyO8vVYb7JMjwTcQUCzEE6ePFn2CgcMGBBWzU+cOCF69OghUqdOLZImTSr69+8vrl69GlYa0USGqTCMGfrOfEeTHq8lARJwHwHNQoiqp02bVjz11FPixo0bYZM4f/68gIhmyZJFCmq3bt3E2bNnw05HywXo+cGbHl7PMTbob0lbSxqMQwIk4B0CYQnhoEGDpLhgcXWkASI6fPhw8fTTT8u0WrduLX755ZdIkwt4na/hWOWEHsLIpTQBcfEgCXieQFhCeO/ePSlezz//fNTgNm/eLMaPHy8KFiwo08Rsb1yz0tFkCAGEGwGMUzKQAAmQgD+BsIQQF3fq1EkK11dffeWflubv9+/fFz179hQ///yzvGb69OmiZMmSMt0aNWqIrVu3ak5La0QsAaI5Ma20GI8EvEUgbCH8/fffpWC9+uqrEZPCLO60adNiXT9//nxRoUKFB+mvXr06VpxIDqBHiLFCOpaKhB6vIQH3EwhbCIGkQYMGUqyWL18eNqGDBw8K2Dy8du1a0GuRbvXq1WUeJUqUCGu3CmaHsR8aC7zx980338hZ46xZs3KMMChxniABbxOISAgxlocZ2Xr16oVF7/r166JXr15i586dmq7bsGGDgKUb5IUlMFpex/H6C5/LuAZ/yv+y2mmiKWNGIgES8BSBiIQQhPBqDKHBThKtYcyYMWLhwoVaoz+It2vXLtG8eXOZX86cOcWkSZMenOMHEiABEoiWQMRCuGrVKilMbdq00VQGvK5OnTpVU9xgkTC5gm1+yZIlExkzZhSjR48W6GUykAAJkEA0BCIWQmSKpS8w4BpqHSBEcOLEidGUM8a1v/76q5x1xtY95P/hhx8KLNhmIAESIIFICEQlhLNmzZK9Qoz7BQqYEMHrcLQ9wUBp4xhmgz/66CMBM1uwjvP+++8/sDoT7BoeJwESIAF/AlEJIRLDlrknnngi1owsTPlDIM2wT3j37l0xatQokTdvXinMMPYAow8MJEACJKCFQNRCCAHCpInatQELM/PmzRPYS4xJDrPD559/LooUKSLL1LRpU7oSMLsBmB8JOJBA1EKIOsOqDJa3rF+/Xr6ezpgxw/JJDLy2K8MLtWvXlmsKHdg+LDIJkIAJBHQRQmyXQ6+wYcOG4siRI2EXGzs+IFr+AWOAjRs3ludwfuTIkf5R5JggvO5hQiZQwHKdihUryvK9/vrrAq4FGEiABEjAl4AuQnjlyhUpNGXKlPFNW9Nn2AuEiOLPN0AEMQmCBdF47YZYwnCCr0ktmNvCd8RFOr7nfNPCZyz3efPNN2U+2Hc8Z84c/yj8TgIk4FECMdUnCgjvvvuuFJnFixdrTgUCpuwF+gshxA/ChzgqKNFUu0T89w7ju298dZ3vf1i9QS8T+RUqVChoT9L3Gn4mARJwNwHdhBCvxBAXWI/RGrAvGH9K4HyvQ68tUA8Pe4aVAKreoLouUHx1zv//nj17RKtWrUT8+PGlbcSxY8eKmzdv+kdzzXcwVj8grqkUK0ICOhHQTQhRnmrVqkkx3LhxY8jiffHFF0IZQggkhBBVNRPtmxgEUpndx4MN8YNxBYwfIs1wAxaDd+nSRTzyyCPi8ccfF0OGDBEXL14MNxlL44MfxknVH3j4ix5YB+JpacGZOQnYhICuQrhp0yYphO+8806c1cNDildiPMAIwYRQnfdNDMIHMVRBjQ9G65gJ5sXQ08yUKZMsG0Tl1KlTKhtb/wcTDCOAC/7wGT8k6ocBvPE91LCBrSvJwpGAgQR0FUKUs3jx4iJhwoQCC6qDBTysvq+x4QghxMpXCIPlEelx7F0ePHiwePLJJ0WCBAmkyTCYDrNzAA9/o7PoNUP8ENAT9D9v5/qwbCRgNgHdhRD2//AAYkF1oAAhw0ywbwgmhDDg6h/wgBsphL75YXvgs88+K+sD3ypazYf5pmHGZ9/en8pPuTBFLxC8/F+VVTz+JwESEEJ3IQTUXLlyiQwZMohz587FYoyHFstisC5Q/WExNo7ju+op+k6K+CYSqPfje96Iz3jFfOGFF2QZMeOMheN2CepHxH9oAD8YagzWrB8OuzBhOUggXAKGCOGECROkaMDrnX9Aj9D/D69tEEIcV+NaOKYmRVQa6N0E6v2o80b/x9rDV155RZahVq1a4rvvvjM6y5Dp47UXTJRFbkwa4QcF44QQR/QE/UUyZKKMQAIeI2CIEIIhHLrnyZNHE07Vq/GNrI4pYcQ5iKP/2kLfa8z6vGTJElG5cmUpQNitgr3VVgXFBL0+/EEU0ePmq7BVLcJ8nUjAMCEcOHCgfCjROwwVlOj5x4MIqgcbs8wQQcS1S0BZ6tSpI8uIXTXwxmd2wHgretK+AeIIXpwl9qXCzyQQnIBhQnj79m1pI/DFF18Mnvu/Z/DABhM49GxwDn92fbC3b98uYOkGog2fz5999pm4c+dOyHpHG0ENFfhPKoEZyhKMabT58noScBsBw4QQoDDxgQfy66+/dhu3gPXBkqG2bduKxIkTS9uIw4YNM1S8IXTg6/8arI5TCAM2Ew+SQCwChgrh6dOn5YP6xhtvxMrYzQewELt79+7i0UcflTO3/fv3F2fOnNG9ynglxnCBb0AvEZMlmDFmIAES0EbAUCFEEeDyE72WNWvWaCuRi2Jhq16/fv3k1r00adJIcTx8+LBuNcSsOsYC1TIk/AdrjBtyplg3zEzIAwQMF0JYqcbDCVuFXg0YL8VrMtZX4rUZrgT0ECpMJvkuRcJ3vg579S5jvaMhYLgQonBly5aVYqjHwx9NZe1wLSZSChQoIHlgggX7sxlIgASsJWCKEC5fvlw++O3bt7e2tjbKfdq0aaJEiRKSS926dcWKFStsVDoWhQS8RcAUIQRSjFthPAsTKAz/I4DF2OXLl5eCiEXa2Kutwty5c+We7ZkzZ6pD/E8CJGAAAdOEEIuNMVaIyQOG2ASwXU/Zc8Q2Pqy/BC/157WZ99iEeIQEjCNgmhCiCjB8miNHDgE/xAyBCcCoreohKhFU/8NxgxA4dR4lARIIRMBUIRw+fLjs4XzyySeBysJj/xKARz4lfr7/P/zwQzIiARIwgICpQojyP/zww6Jw4cIGVMU9SWKHiq8Aqs/oUWMP99mzZ91TWdaEBGxAwHQhxI4LPNhffvmlDapv3yJgN4oSQPx/9dVXxX//+1+RNm1a6U4An+FvhYEESCB6AqYLIXZb4MEuV65c9KV3eQonT54UMKiQO3du8fLLL8vaXrt2TeAVGVvo4HAKS5L27t3rchKsHgkYS8B0IUR1lKWWZcuWGVs7l6SuDN367hq5f/++9NwHm4/wrQK/0lu2bHFJjVkNEjCXgCVCCGdI6BXWrl3b3No6ODeMD7755psBazBx4kQ57gqmb731lli9enXAeDxIAiQQmIAlQoiiVKpUSYrhtm3bApeMR2MQwOswhO6nn36Kcdz3CxZeKyvVVatWFYsWLfI9zc8kQAJBCFgmhHCAhAe7ZcuWQYrGw74E/vzzT5EkSRJNvBYuXChee+01yRdrEr/66ivfpPiZBEjAj4BlQohywDNc0qRJxbFjx/yKxa+BCHTs2FGKm9blM3hFrlmzprwG/qYnTZoUKFkeIwHPE7BUCGG5Gr1CLAVhCE3g6NGjklfPnj1DR/aJgeEHmEEDa1i+GT16tIBpMAYSIIF/CFgqhCjCU089JR577DHx119/sU00EIBjJngIjMQnyv79++Wr9UMPPSRtI8Ld6h9//KEhV0YhAXcTsFwIP/30U9lTGTp0qLtJ61Q79O7Qs4P/4kjDiRMnROfOnUWKFCnkj1CvXr1i+T2JNG1eRwJOJGC5EAIazNjny5fPifwsKTN8KcPadbQBvcHevXuLDBkySP8qnTp1Evv27Ys2WV5PAo4jYAsh/OCDD2QvZ/LkyY4DaEWBly5dKnnNmDFDl+xv3bolPv74Y2kZKFGiRKJFixYCLkoZSMArBGwhhBgfjBcvnlwD5xXw0dazaNGi0mZhtOn4Xw/LQOid4/W7QYMG9IHiD4jfXUnAFkIIsm3atJEPn6+FZlcS16lSU6dOlbyM2qYIR1AQWwhijRo1BHqhDCTgVgK2EUIM4OOhw44IBm0EcubMKXfoaIsdWSy4C4DBB7QNLODMmTMnsoR4FQnYmIBthBCMatWqJR847DphCE1AGbrdsWNH6MhRxkDPE+4CIIilSpUS6DEykIBbCNhKCPFA40F7++233cLX0HpgkgMOsZo0aWJoPr6J40cKxjLQToUKFRJjx471Pc3PJOBIArYSQhB86aWXRPz48cXPP//sSKBmF/r999+XonT8+HFTs961a5f8wYIgwl7i4MGDuSje1BZgZnoSsJ0QqqUhWPDLEJoA3KNCjLp06RI6sgExDh8+LCe6EiZMKJ544gnRt29fce7cOQNyYpIkYBwB2wkhqvrss89Kk/SwuMIQmgCMssIXzNWrV0NHNijGmTNnpA9mvKpjgTyEGXujGUjACQRsKYTKixu9tmm7hfbs2SN7hdg7bHW4cuWKwAJ57B+HZaFWrVqJH3/80epiMX8SiJOALYUQJYZFZj22kcVZexedxFo/vJraJdy7d08MGzZMGtXAq3vjxo3Fhg0b7FI8loMEYhCwrRBi8B0PEIwyMIQmANuD4PX555+HjmxyjPHjx4vnnntOlg/uBoxaBG5ytZidiwjYVgjBGONeMN7KoI0AzPQXLFhQW2QLYmFv9IsvvigFEYYjYI+SgQTsQMDWQoiZY/RyZs+ebQdWti8DOIEXXIDaOWAbJdy5oqxYLjVt2jQ7F5dl8wABWwshlmHgYalYsaIHmkKfKj7zzDOO8Rm9atUquaUSbVykSBEOg+hzCzCVCAjYWghRH1hkxoOycuXKCKrnvUvGjRsneTlpYgL+mOvVqyfLnTdvXjnJYpeWw0J1TPSg54pxznbt2tmlaCyHjgRsL4QwFAohhL9eBm0EMmbMKOrWrastso1iwVXpO++8I9s7W7Zsol+/fuLatWuWlRD7qXHvValSRe6t/v7772mWzLLWMDZj2wshqq9cU+7du9dYGi5JHQKCB/jgwYOOrBF6Yeh5YR1i+vTp5ULt3377zdS6XL58We7jHjFihKn5MjNrCDhCCNesWSMf7LZt21pDyWG5wgR/ggQJhNN5XbhwQXo4xE6VZMmSyfocOnTIlNaAAGbNmtWUvJiJ9QQcIYTABCOhjzzyiDh//rz11BxQgvfee0/AW50beMGCOXYZYcE4erqwTrRz505DWwFLkdR44O7du8XatWsNzY+JW0vAMUKolob06dPHWmIOyR09J4gGjCC4KcAnM6zdoG516tQxTKBSpkwphRATJOgZ4rsbebrp3oimLo4RQlQSPpD5uqK9uTHBhDG2+/fva7/IITHh6Av2ECFOlSpVEosXL9a15EgX4ocJEhXwGcd9j6lz/O9sAo4SQjgWwo04atQoZ1M3qfSbNm2SvMaMGWNSjuZngzcFWMzGfQGXAjNnztSlEEhPvRr7Juj7yux7nJ+dTcBRQgjUGDgvUKCAs6mbWPoKFSqI//u//zMxR2uygh1L+FSBgGFb5oQJE6IqSP78+UWgYRgspYEYMriLgOOEsFevXvJm57YsbTfiwoULJa+vvvpK2wUOj7Vu3TrpdQ+CCLekkS5/wUJ+iJ5/CCaQ/vH43VkEHCeEMD4KH8ivvPKKs0hbWFqMpZUsWdLCEpifNWaV4ZcZgvjkk0+KAQMGiL///ltzQbCWEdeOHDnywTVqgTVmkRncRcBxQgj8LVq0kDcpfe1quxkxsYCH2ovbFOH7BvcLfjyx4wY+XrRaPofwYcIEVrfxh8/03qftnnNaLEcK4S+//CIfbNi2Y9BGAFvWqlWrpi2yC2PBtwusGSVPnlykSJFCToT8+uuvIWuKHSbcWhcSk+MjOFIIQb169epSDI1eWOv4Fv63AsrQrddf69AbxNpKLCuCt0TsbT5w4IBbmpn1iJCAY4UQFkvwugfHRQyhCVy/fl32hvDgMwhx9+5dMWTIEJE9e3Z5H8H6zfbt24nGowQcK4RoL5hGSpw4scBrD0NoAl27dpUP/alTp0JH9lAMuIOAHUf8sGKmGG4PGLxFwNFCqJaGdO/e3VutFmFtT548KR928goMcPr06eL555+XjGBBG5a0GbxBwNFCiCaCD+RMmTKFtTTCG00buJZNmzaVxitgyIAhMAG4OihTpowURPhYgUAyuJuA44UQXtvwSoPJAIbQBDC5BF5Dhw4NHdnjMVasWCHgZAq8YHyBHhXde0M4XgjRNPCB7IVtZHrdhhgHy5Ejh17JuT6dzZs3i1q1aklBhOEP/ui6r8ldIYSwVYdfbTv69LXjLbN8+XLJa8qUKXYsnm3LBAvpsIWIey1z5swC2z1v375t2/KyYNoJuEIIsRQCPpBLlCihveYej1m8eHHpOc7jGCKqPhb0w/o3rIBjx0nHjh3FxYsXI0qLF9mDgCuEECg7dOggf6nt7tPXHs0upLkq9Gz0tuNnl/qZUQ64m+3Ro4fcepcwYULRvHlzceLECTOyZh46E3CNEMK5Dx7sypUr64zIvcnB0jMcYzFER+DGjRti4MCB8nUZ92D9+vUFPPIxOIeAa4QQyGGRGTcidp0whCYAs/fkFZpTODFgNDhnzpySK7aB8l4Mh551cV0lhD/++KO8AeGQmyE0AZilSps2rTRXFTo2Y4RDABN3sF2IHxoYx8VSHAb7EnCVEAKz8oEMe3IMoQn07t1bPqxHjhwJHZkxwiYAg7jFihWTjGETct68eWGnwQuMJ+A6IcQvL36FMXnCEJrA77//Lnm1b98+dGTGiJjAkiVLRNmyZSXrggULCi5dihilIRe6TghBCT6QU6dOLbiNTNs907p1a5EoUSJx6dIlbRcwVsQEYNsQC9rxY/30008LNzvWihiSBRe6Ugi//PJLeaP179/fAqTOy3L//v2SF8zZM5hDYMeOHQ8m97JkySI++ugjczJmLgEJuFIIUVNshYKvCgZtBGrXri2Xf2iLzVh6ETh48KBcf4geIt5i4EqAbzJ60dWejmuFEN7LcHONHTtWOw0Px4T3N/D67LPPPEzBuqrDbUCnTp2kfc0kSZLInSvnz5+3rkAey9m1Qoh2xNKQIkWKeKxJI68uPAPCrBmDdQQwTouZfPQO8cPUpEkTgS19DMYScLUQ4jUDN9Ps2bONpeiS1LG0A7zmzp3rkho5txp37tyRVm4wfog2qVmzpsA6WQZjCLhaCPHr+tBDD8kFrcbgc1+qsLsHo6QM9iEwbtw4OcMMQaxYsaLYuHGjfQrnkpK4WgjRRs2aNZO/qBgDYwhNYMKECZIXlnkw2IvA1KlTBdYgQhBLly4tli1bZq8COrg0rhfCQ4cOyRunbt26Dm4mc4sOQ7f0GW0u83BywxAGdqlAEAsXLizmzJkTzuWMG4CA64UQdVY+kCGKDKEJKEO3tKASmpWVMWBgV20phYX2SZMmWVkcR+ftCSHcsGGD/PXEDgqG0ATgBB1LOFq0aBE6MmNYTmDTpk2yB48eYtasWQUs4DCER8ATQggk8IGcLFkyceXKlfAIeTQ21rThwYKdRwZnEMCsMiwvod3SpUsnuFNIe7t5Rgjnz58vb5CePXtqp+PhmFi7hgeKvJx3Exw9elS0adNGth9cWHTr1k1cu3bNeRUxscSeEUIwhX04rMti0EagUaNGcmEv1rQxOI8ALAt1795dvgnhR61Vq1bi7NmzzquICSX2lBBi+xhuiOHDh5uA1vlZbNu2TfIaOXKk8yvj4RqgNwgDJHhdxv3fsGFDcfjwYQ8TiV11Twkhqo8eIbeRxb4Rgh2Bg/NcuXIFO83jDiOAPfjZsmWTglitWjWxc+dOh9XAmOJ6Tgjxy4hfxRkzZhhD1GWpLl26VPKaPn26y2rm7epMnDhR5M2bV7YtDMZ6fcOB54Tw5s2bcswEs8gM2gi88MIL0ty8ttiM5SQCs2bNkoaM0TmAQWNY0vZi8JwQopHhnBsNv3LlSi+2edh1njZtmuTFLV1ho3PMBYsWLRIvv/yybOdnnnlGQCCdHrBNdO3atfLv8uXLcVbHk0J46tQp2eDYccKgjQBcVFaqVElbZMZyLIE1a9ZI3+DoKOTIkUNg77nTQp8+fR6Mg6Ie6i+u/fOeFEI0rPKBzG1k2m5zzLTjhoKJeQb3E9i+fbuoV6+ebPMMGTI4ZqUFlnzhPoUY+vYCFyxYEGejeVYIf/jhBwkM1mkYQhO4deuWSJUqlTQUGjo2Y7iFAPzZvPPOO/JZSZ48ufjggw/EvXv3bFm9L774QpYzrp5fsIJ7VggBBLbdEiRIIC5cuBCMD4/7EFCGbo8dO+ZzlB+9QODkyZPSRW78+PGljc/OnTsL7Em3U0iZMqVAjzCS4GkhxOA/utFdunSJhJ3nrjlz5ozkhYeAwZsELl68KHr16iUeeeQReS80b95cnD592nIYePXFs3z8+PGIyuJpIQQxLA1Jnz59RPC8eBFufOxfvXr1qherzzr/S+D27dvi448/FpkyZZIChDF3eOSzKqAnCMs7kQbPCyGs/uKXhH5ltd1Ce/bskbwGDRqk7QLGcj0BOKnHqgI8R5UrVxaYaDE7wGI3/iINnhdCgMMWsty5c0fK0HPX1ahRQzzxxBOeqzcrHDeBKVOmCPi8gSDC783q1avjvkDHsxRCHWAOHTpUNt7kyZN1SM39SeAGx82ObVoMJOBP4OuvvxYlSpSQ9whcCSxcuNA/iu7f8WoMEY40sEf4Lzn4QC5WrFikHD13HX6BCxQo4Ll6s8LaCWAyskKFClIQ8cZl5P5+tXQG/yMJFMJ/qXXt2lU22LfffhsJR89dA4dB6BWGWqjqOTCscCwCcJWB4RTcL4899pj49NNPY8XR40CVKlVkHu3btxcwHde3b19psXv37t0hk6cQ/osIawnhAxlmpxi0EcCe1HLlymmLzFieJwBBUjs/sOZvyJAhujNBj1CNF+I/8tOypIZC6NMUagU9bbT5QInjIxyP41cev/gMJKCVwJEjRwQcqeHewYaG3r17C6utoFMIfVoP24nQOA0aNPA5yo9xEciYMaOgz+i4CPFcMAJwDIYhqUSJEsnnrkOHDgILtq0IFEI/6mosA7soGEIT6Nevn7yJDxw4EDoyY5BAAAJYnI/7KHXq1PJewv5/bOnzDdjOd+7cOd9Dun6mEPrhhP0y9ArbtWvnd4ZfAxHALzheb+A1jYEEoiFw//59aeUGa1TxDNapU0fs27fvwbgijr3xxhvijz/+iCabgNdSCANgwWJQDOba1cpGgCJbegg/GphoOn/+vKXlYObuITB+/HiRJ08eKYgQQN8/mAfTO1AIAxBVS0Mw/c4QmsChQ4fkjUpeoVkxRngEVO/QVwix113vQCEMQhQ+kLNnzx7kLA/7E8CmexivwOsNAwnoReD555+P0RuEIMJytt6BQhiE6NixY2UDwBcyQ2gCmzZtkrywAZ+BBPQgAM+Jvj1B9XnYsGF6JB8jDQphDBwxv8AHcqFChWIe5LegBLCdCuM6DCQQLQHldheTI7Nnz5ZO6WvVqiVmzpwZbdIBr6cQBsTyz0GMeeFX6JtvvokjFk8pAvCEBl5u8ICm6sT/5hN4++235X3UqlUr0yz4WRIAABhbSURBVDKnEMaB+vr169IHMhxgM2gjAGsjJUuW1BaZsUjAh8CVK1ceuBSF0VczA4UwBO333ntP/jpt3bo1REyeBgGYMkOvkD6jeT+EQwAGfzEJkjhxYkveKCiEIVoLjorwYGN8gkEbgWzZsolq1appi8xYnicAe4VYhwoDyZs3b7aEB4VQA/b69etLMdRixUJDcq6PMnjwYMlr165drq8rKxgdgVGjRsl7BcNPVjqBohBqaMdt27bJxmrRooWG2IyCsVX4wKXPaN4LcRGAkQW8bTVt2jSuaKacoxBqxAwfyEmSJBE3b97UeIW3o3Xr1k3e5KdOnfI2CNY+FoG///5bVK1aVd4fcBhvh0Ah1NgKixcvlg333//+V+MV3o4G6yH4te/evbu3QbD2MQhgeEk5eIKzJ7sECmEYLQEfyJkzZw7jCm9HxSsPHIH/9ddf3gbB2ksC33//vUiVKpX0gLhmzRpbUaEQhtEcamnI6NGjw7jKu1Fh6Ru9QngJZPA2AeVcCWtMjx49ajsYFMIwmwRT/PDVwaCNABzq0HiFNlZujdWnTx/5gwjDHHfv3rVlNSmEYTYLVryjlwNTXQyhCSxfvlzyitTNYugcGMPOBJSzph49eti5mIJCGGbzwFgrfCCXKlUqzCu9Gx3OvosUKeJdAB6sOYz04hlBp8EJFpwohBHcpGppyPr16yO42nuXwGIIHgjMvDO4nwDGhmFQNV26dMIpfsIphBHcl2fPnhXx48cXGP9i0EYgd+7c4rXXXtMWmbEcS2DevHnyRw9vAPAK6ZRAIYywpZQP5MOHD0eYgrcuw0w7eoVbtmzxVsU9VFsYTEUbwxPktWvXHFVzCmGEzbV3717Z6E2aNIkwBW9dht0EGFvFvm0G9xFo27atfB46duzoyMpRCKNoNvzywWoG7KgxhCagllGwFx2alVNi3LhxQ1SqVEmK4MiRI51S7FjlpBDGQqL9wKpVq+QN0KVLF+0XeTgmHHTHixdPtG/f3sMU3FP1n3/+Wa6pTZo0qZg/f76jK0YhjLL54AM5TZo0Uabinctbt24tEiVKJC5duuSdSruwpjC8CwtD+fLlE5gldnqgEEbZgmppiBGetaIsmi0vx0wiBtQHDBhgy/KxUKEJTJw4Ubbh66+/Li5cuBD6AgfEoBDq0EjwgfzUU0/pkJI3kqhduzaNVzi0qWF9CT9kZjpWMgMVhVAHymppyIwZM3RIzf1JrFu3Tj5Mn376qfsr66IaYq8wRHDQoEEuqtU/VaEQ6tSkWElftGhRnVJzfzIwzY7xJQb7E/j1119F8eLFpQi61VUrhVCn+1D5QMZMMkNoAphlRO9i7ty5oSMzhmUEsAAeNjjhYW7Tpk2WlcPojCmEOhH+888/5Swat5FpBwpLxZh1Z7AngdmzZ8sfK6sdK5lBh0KoI2XlA3nfvn06purepCZMmCAfNFguZrAXAWVu7u2337ZXwQwqDYVQR7BHjhyRD3a9evV0TNXdST3++OOiZs2a7q6kw2rXsmVLeR/bxbGSGfgohDpTVj6Q//jjD51TdmdyH374oXzosHebwVoCFy9elBaCMHbrNUO6FEKd7z0MKONGateunc4puzM57NPGFi36jLa2fffs2SPy5Mkj0qdPL1avXm1tYSzInUJoAHT4QMb2IwZtBDp16iR/PH777TdtFzCWrgSWLl0qfXbDkrgdHSvpWtkgiVEIg4CJ5vCCBQvkg/3RRx9Fk4xnrv3ll18kr549e3qmznapKBa14w0G49p37tyxS7FMLweF0CDk8IGMRdYM2gjAyU/q1Kk9/TBqI6VfLOVywu6OlfSrcfCUKITB2UR1Rm1M99qgc6TQtm3bJnsmI0aMiDQJXqeRwM2bNwX2e6MnyG2O/0CjEGq8eSKJ9vTTTwssGmbQRgDWTGi8QhurSGNhiRe2gj788MOOcawUaV3DuY5CGA6tMOOqRalO8eQVZvV0jw5O6KVMnz5d97SZoBBYuJ4hQwb548xF/zHvCAphTB66frt9+7Z0afjyyy/rmq6bE8PYarFixdxcRUvqhh8X/Mg40bGSGcAohAZTVgPSu3btMjgndyQ/bdo0+cAuW7bMHRWyQS0GDhwomXbo0MEGpbFnESiEBrcLTBjBBzK3kWkHnTNnTukQSPsVjBmMgHI7y0moYIT+OU4hjJuPLmfVzcgFw9pwDh8+XPZgtm/fru0CxopFAPdauXLlJEenO1aKVTkDDlAIDYDqnyReizE+g83sDKEJYGw1VapUonHjxqEjM0YsAliKhNl39Kx/+OGHWOd5IDYBCmFsJoYcwSA1vLfdu3fPkPTdlqjyjXHs2DG3Vc3Q+sybN08kTJhQGk9wi2MlQ4H9mziF0AzKQojvvvtO9gq9ZNooGrRnzpyRvDp37hxNMp66dtSoUXzziLDFKYQRgovkMiyjwTouBm0EmjdvLhf+Xr16VdsFHo6lDFe40bGSGc1KITSD8r95wMsdxgrHjx9vYq7OzQqmocCLxiuCtyFcRGDYBZzgY5shMgIUwsi4RXwVttzB7huDNgJ4yLNkyaItssdiYXdIoUKFRMaMGV3tWMmMZqUQmkHZJw/lA3nhwoU+R/kxGIE1a9bI3g6MWDD8jwDGnNOkSSNKlSolsFaVIToCFMLo+EV0NcxzwU8sgzYCL730kihQoIC2yB6IpSwbecWxkhlNSiE0g7JfHsoH8tatW/3O8GsgAnPmzJG9Qhi89Xro06ePZIF7iEE/AhRC/VhqTgmOnWDKv1KlSpqv8XrEZ555Ru6U8CoHWI9u0qSJFMHJkyfHiQHb6WgHM05EsU5SCGMhMeeA8oF84sQJczJ0eC7jxo2TIrB+/XqH1yT84mNReZkyZeSPZyjHShBBzCCXLl06/Iw8fAWF0KLGP3jwoLxhmzVrZlEJnJctZkfr1KnjvIJHUWIIf/bs2UXBggUFjKrGFXbv3i3vKbg9oBDGRSr2OQphbCamHWnQoIG8cW/dumVank7OqH///pLXgQMHnFwNzWXHusB48eJJs/paHCvlz59fYAwRfxRCzZhlRApheLx0jb1u3Tr5YGNfLUNoAnBAjn20bdq0CR3Z4TEGDx4s743u3btrqgn8aCvxoxBqQhYjEoUwBg7zv8BPx6OPPmp+xg7NEQ/8Qw89JM6fP+/QGoQudtu2baUIanWsBBP8KVOmFMePH5eJUwhDM/aPQSH0J2Lyd1gLweD2J598YnLOzszu0KFDkpcbl4+cO3dOVKlSRdYPTte1hMuXL4ts2bLFmCWmEGohFzMOhTAmD0u+wUdHjhw5LMnbiZm+9dZb0heMm0yawW4gxvhy5colwnGsBOHEn2+gEPrS0PaZQqiNk6Gx1E6BuXPnGpqPWxLfvHmzq3rR33zzjXy1xTBJOJZ21Cxx+/btBXrI6g87cdBLxHe8NjOEJkAhDM3IlBjwgVy4cGFT8nJDJq+++qorjFeMGTNGinokjpUghJgg8f/LmjWrFFYc58JqbXc7hVAbJ8NjKR/IGzZsMDwvN2SwaNEiKSCzZs1ybHUwI4zxYb0dK/HVOPxbgkIYPjNDrrhx44Yc9ypfvrwh6bsxUfSgS5Ys6biqXbt2TdSvX1+KICbL9A4UwvCJUgjDZ2bYFaqHcPjwYcPycFPC2HOLHtXKlSsdUy3sKIJ4Z86c2TDHSlhGg9dmBu0EKITaWRkeE/uO4QO5YcOGhufllgwwKVC1alVHVAeCDSOzGLtz8zpIRzSGXyEphH5ArP767rvvyl5OOLOHVpfZyvyHDBkiecFlqp2D6r3CxzWD/QhQCG3WJnBqjte9rl272qxk9iwOxlZTpEgh7Gy8ol+/frJN6XvFnvcQSkUhtGHb1KxZU3pvs2HRbFmkbt26SaE5deqUrcqHBd+qh0/HSrZqmliFoRDGQmL9gW+//VY+2MOGDbO+MA4owcmTJyUvrQYKzKgSylSxYkXxyCOPiI0bN5qRJfOIggCFMAp4Rl4KH8iPP/64kVm4Ku2mTZvKV2S8KlsdNm3aJPLmzSs9zNmtl2o1G7vmTyG0acsoH8hffvmlTUtor2Lt3LlT9goxeWJlmD17tkiWLJmoW7eulcVg3mESoBCGCczM6PCBnC9fPjOzdHReWEYDa85WBQxlYKKrd+/eVhWB+UZIgEIYITgzLoNpLjxYofxUmFEWJ+SxYsUKycuK/bUwfIC2CuVYyQkcvVhGCqGNW/3+/fsCPpBhTYRBG4ESJUqIIkWKaIusQ6wLFy4IzPLDWOyqVat0SJFJWEGAQmgF9TDy/OCDD2RPY//+/WFc5d2oWKaCntnixYsNh4BtbC+88ILInTt3SMdKhheGGURFgEIYFT7jL4bVYvhA9pr3tmjIQphgpsvIAKHNlCmT9E19+/ZtI7Ni2iYQoBCaADnaLOCnA70cOIZnCE1g9OjRkhcMuBoR4EsE7dGxY0cjkmeaFhCgEFoAPdwsf/rpJ/ngYUCeITQB7OhIly6dNHUVOnZ4MeBxECIIh/MM7iFAIXRIW8IHMizTMGgjAJt8ECy9TJr99ddfAo7TkaZWx0raSspYdiBAIbRDK2goA3xP4CEcNGiQhtiMgrFVOEfXoxcNMVU7fdA7Z3AfAQqhg9oUzn3wysegjUDr1q1FokSJxKVLl7RdECAW1nDCs1yZMmXElStXAsTgITcQoBA6qBXnz58ve4VWLBh2EKYHRcWSI/Si+/fv/+BYOB+mTp0qEidOLJo3bx7OZYzrQAIUQoc1Gnwgw+MdgzYCtWvXlstctMX+X6yBAwdKER06dOj/DvKTawlQCB3WtJ9//rl8QJctW+awkltT3PXr10teWPKiNbRs2VJeY4RjJa1lYDxzCVAIzeWtS27oERYvXlyXtLyQSNmyZTUZrzh9+rRcIJ0qVSqxY8cOL6BhHf8lQCF04K0wePBg2WOhpzJtjafGVufOnRv0gq1bt4oCBQrIfcp0rBQUk2tPUAgd2LRw7JQ+fXpRvXp1B5bemiLDpFkw4xVff/21SJs2rXjrrbesKRxztZwAhdDyJoisAMoH8tmzZyNLwGNXTZgwQfai16xZE6PmI0aMkMf79u0b4zi/eIsAhdCh7X306FGRIEEC0apVK4fWwPxio9eXNWtW2ZPGEqROnTpJEaQVcPPbwm45Ugjt1iJhlEd5SIPdQoa4CSxatEiKHtYVqj/YENywYUPcF/KsJwhQCB3czNu2bZMPNfzmMsRNoEqVKg8EUAkheogMJAACFEKH3wewjgyXkQxxE8BCdCWAvv/v3r0b94U86wkCFEKHNzMWVuPBxmQAQ3AClStXjiWE1apVC34Bz3iKAIXQBc0NyyjZsmVzQU2MqUKPHj2kCJYqVeqBGMKC9ZkzZ4zJkKk6jgCF0HFNFrvAmPVEr3DhwoWxT3r4yLVr16RxVrBRjpWuX78uuGDawzdFkKpTCIOAcdphtSvCaeU2qrywPIMeYJYsWXQzzmpUWZmu9QQohNa3gS4lUD6QMZPs9YBxUzh6f+WVVwQdK3n9btBWfwqhNk62j4XZTywWrlSpku3LamQBx48fL10atGjRwshsBJbjLFiwwNA8mLh5BCiE5rE2PCflA/nkyZOG52XHDHr27CnHSocPH65b8eBB0H+P8vHjx2U++M/gDgIUQne0o6wFZkFTpEghmjVr5qJaha4KXn8bNmwoxUlPx+7wE5MyZUqZ7uXLlx8UBPuTS5cu/eA7PzifAIXQ+W0YowbKB7JXxsYOHTok/YmkTp1a7N27NwaLaL9A7BRPiKIKeC32/a6O879zCVAIndt2AUsOMcByEbwmuj0sX75cPPnkk6Jo0aK6O1bC+B96g+o12Hc8EGOxDO4iQCF0V3vK2sAHMpwOuTnAZQE81NWvX9+QakLs4BsZIX/+/A8+QxDpPMsQ5JYmSiG0FL8xma9du1b2CseMGWNMBhan2rt3b1k/o4xNQOjQG1TjguoV2eJqM3sDCVAIDYRrZdJvvPFGRN7brCxzqLxhbqxJkyZSBGfNmhUqekTnIX7wWaJ6g0ikUaNGnByJiKZzLqIQOqetwiqp8tMBM/RuCMeOHZMLpPE6bKRjJQggxlj9/2Dqn8G9BCiE7m1b8eKLL8rxLadXEeb1c+XKJfLmzSvOnTtnWHV8e4OYFVZ/ShwNy5gJW06AQmh5ExhXAOUD2clWmCdPniySJEkizDCZhVfgQDPCEET0ELmA2rh71eqUKYRWt4DB+efOnVtUqFDB4FyMSV7tlOnatasxGfikqpbJBJoRVue4dtAHmMs+Ughd1qD+1VE+kI8cOeJ/ytbfmzZtKnthEydONKWcWCQdqDeoMkePMJBIqvP872wCFEJnt1/I0l+6dEn6QMZrnxPC6dOnRfny5aUIrlu3zglFZhldQIBC6IJGDFUF5QMZhkrtHDZu3CjwKo+emVcNR9i5fdxcNgqhm1v337rhtRg+kM0Ya4sU54wZM0SyZMlEuXLlIk2C15FAxAQohBGjc9aFzZs3l6+bdiz1gAEDZNnorN6OreONMlEIvdHOQvlA1tNWnx7olJP6kSNH6pEc0yCBiAhQCCPC5syL3nzzTQFzVXYIWBgNT3KYjV26dKkdisQyeJgAhdBDja98IM+cOdPSWqN3il0iadKkoWMlS1uCmSsCFEJFwiP/4dAoT548ltV29uzZ0op2sWLFxK1btywrBzMmAV8CFEJfGh74rHwgY/+u2eHjjz+Wr8Iwq89AAnYiQCG0U2uYVBb4QC5TpoxJuf2TTcuWLaUIYoaYgQTsRoBCaLcWMaE8ygcynKAbHWDR5fXXX5ciiNdi/4D9uzAkiz8GErCKAIXQKvIW5nvz5k25e6Nu3bqGlmL37t0iX7580nrMrl27YuQFT3AwgIpdJLAAjdljuM1UVqFjROYXEjCYAIXQYMB2TV5Zdrl48aIhRYRvDwgdhPDPP/+MlYe/JzgIIEQRxxlIwGwCFEKzidskPxg3gA/kDh066F4i9PbQw6tevXpYacMAKsSTgQTMJkAhNJu4jfJr3769FCw9i6T8AMPQQ7gBQgiPcQwkYDYBCqHZxG2Un/KBPGjQoKhLdf36dflai57gpEmTIkoPr8YQUgYSMJsAhdBs4jbLD2v6kidPHlWp9u3bJ+DcCCIYqVsA9AZ9XWhGVSBeTAJhEqAQhgnMbdGVD+QpU6ZEVLUlS5bI/cvZs2cXv//+e0RpKD/CmGVmIAErCFAIraBuszzhAzlnzpxhlwoO5NELhEXpSANEEGnQH0ikBHmdHgQohHpQdHgaygfyd999p7kmnTt3lgLWpk0bzdf4R1Q9QfoC8SfD72YToBCaTdym+cEHcvHixUOW7s6dO6JmzZpSBEeNGhUyfrAISgT5OhyMEI+bSYBCaCZtG+SFV9C+ffvGKonygfzjjz/GOqcOHD58WBQuXFiKIEx6RRogfngdrlq1qiwLyuP7x9fkSMnyukgJUAgjJefA67B7I1u2bFKEAvXE4DipRo0aAWu2YsUKkTZtWpEuXTpx9OjRgHG0HkTe2FYX7I+vylpJMp5eBCiEepF0QDpqwXKwyYkhQ4ZIkTx79myM2kyYMEEe1/LqHONCfiEBhxCgEDqkoaItJnqD2L6mxuawDc4/YN8xen0lSpQQ/fr1E9u3bxfvv/++FMHGjRv7R+d3EnANAQqha5oy7opgxwZ2biDglRS9Q/+AnSZJkyaVwodeo/obOHCgf1R+JwFXEaAQuqo5A1fm+PHjUtTUJASEMJCVl6ZNmz4QPyWC6dOnD5woj5KAiwhQCF3UmMGq0qhRI9kLVOfRG4QY+gcsoVEC6Ps/kBkt/2v5nQScTIBC6OTW01B29AIhapgthuFT/OFzIHNXXbt2jSWERYsW1ZALo5CAswlQCJ3dfiFLj54fTFuhF6j+0EOEOPoHWJCBUKreYObMmWlC3x8Sv7uSQOynwZXV9GalVG/Qf81gsOOK0pYtW8TKlSvFvXv31CH+JwFXE6AQurh5MUuM3p9/wFIa9PrU5In/eX4nAa8RoBC6tMWxXhBihxnjQAHnAq0lDBSXx0jA7QQohC5tYbwO+78S+1YVvcFgIukbj59JwAsEKIReaGXWkQRIIE4CFMI48fAkCZCAFwhQCL3QyqwjCZBAnAQohHHi4UkSIAEvEKAQeqGVWUcSIIE4CVAI48TDkyRAAl4gQCH0QiuzjiRAAnESoBDGiYcnSYAEvECAQuiFVmYdSYAE4iRAIYwTD0+SAAl4gQCF0AutzDqSAAnESYBCGCceniQBEvACAQqhF1qZdSQBEoiTAIUwTjw8SQIk4AUCFEIvtDLrSAIkECcBCmGceHiSBEjACwQohF5oZdaRBEggTgL/D1MjnInvTePyAAAAAElFTkSuQmCC[/img]
[size=150]Right angle [math]ABC[/math] is taken by a dilation with center [math]P[/math] and scale factor [math]\frac{1}{2}[/math] to angle [math]A'B'C'[/math]. What is the measure of angle [math]A'B'C'[/math]?[/size]
Use the applet below:
[list][*][size=150]Dilate point [math]C[/math] using center [math]D[/math] and scale factor [math]\frac{3}{4}[/math].[br][/size][/*][*][size=150][size=150]Dilate segment [math]AB[/math] using center [math]D[/math] and scale factor [math]\frac{1}{2}[/math].[/size][/size][/*][/list]
A polygon has perimeter 12. It is dilated with a scale factor of [math]k[/math] and the resulting image has a perimeter of 8. What is the scale factor?
[size=150]Select [b]all [/b]the statements that [i]must[/i] be true.[/size]