Atividade II.I: Alturas e Ortocentro - Material Virtual
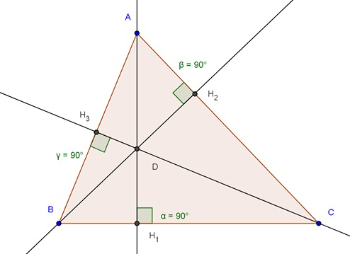
Relembrando...[list][*]A [b]altura[/b] é o segmento que vai de um vértice até o lado oposto, fazendo 90°;[/*][*]O [b][/b] [b]ortocentro[/b] é o ponto de encontro (interseção) entre as três alturas de um triângulo.[/*][/list]

Siga o passo a passo abaixo:
Passo 1: usando a janela 4, construa um triângulo qualquer no applet abaixo;[br]Passo 2: na barra de ferramentas, utilize a janela 3: "Reta Perpendicular" e trace a reta perpendicular ao lado oposto do vértice A, passando pelo vértice A. Faça o mesmo para o vértice B e para o vértice C;[br]Passo 3: na barra de ferramentas, use a janela 2 e a opção descrita como "Interseção de Dois Objetos" para marcar o ponto de intersecção entre as retas perpendiculares;
Com base no applet acima, responda as questões:
1. Na barra de ferramentas, use a primeira opção e movimente os vértices do triângulo para alterar a sua forma e observe. As alturas se interceptam em um único ponto?
2. Este ponto permanece sempre na região interna do triângulo?
3.Qual é a posição do ponto D, de intersecção das alturas do triângulo quando ele for acutângulo?
4. Qual é a posição do ponto D, de intersecção das alturas do triângulo quando ele for retângulo?
5. Qual é a posição do ponto D, de intersecção das alturas do triângulo quando ele for obtusângulo?
6. Que posições são possíveis para este ponto?
7. É possível prever quando o ponto de intersecção ficará na região interna, na região externa ou sobre algum vértice do triângulo?
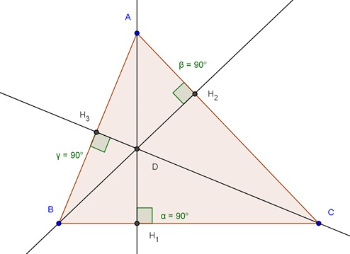
8. Chamamos os segmentos AH1, AH2, AH3, contidos nas retas perpendiculares, de alturas do triângulo relativas aos lados BC, AC e AB respectivamente. Qual é o nome do ponto de intersecção entre as alturas de um triângulo?