
Lembar Kerja Peserta Didik 2

Petunjuk Pengerjaan
1. Isilah identitas dengan benar pada bagian yang disediakan[br]2. Kerjakan aktivitas bersama dengan kelompok masing-masing
Tujuan Pembelajaran
1. Melalui kegiatan diskusi, peserta didik dapat menentukan jarak dalam ruang (antar titik, titik ke garis, dan titik ke bidang) dengan benar. [br][br]
Identitas Kelompok
Pilih kelompok sesuai pembagian kelompok
Ayo Mengingat
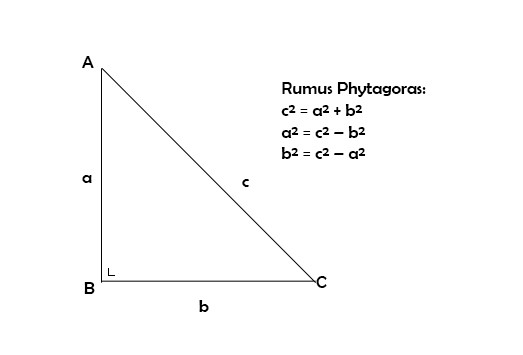
Teorema Pythagoras merupakan salah satu konsep matematika dasar yang ditemukan oleh matematikawan Yunani kuno, Pythagoras, dan dinyatakan dalam bentuk persamaan matematika sederhana yang menggambarkan hubungan antara sisi-sisi sebuah segitiga siku-siku.
Ayo Mencoba
Diberikan kubus ABCD.EFGH dengan rusuk 10 cm. Tentukan jarak antara titik E dan titik G.[br][br]1. Dengan menggunakan menu yang ada, gambarkan ruas garis yang merupakan jarak antara titik E dan titik G.
2. Setelah menggambarkan jarak titik E dan titik G, bentuk bidang segitiga untuk mempermudah mencari jarak antara kedua titik menggunakan teorema Phytagoras.
3. Dengan menggunakan teorema phytagoras, berapa jarak titik E terhadap titik G?
Ayo Menalar
Sebuah kubus ABCD.EFGH dengan panjang sisi 12 cm. Bagaimana cara menghitung jarak titik H ke garis AC?[br][br]4. Garis HI merupakan jarak titik H ke garis AC. Gambarlah garis HI yang merupakan garis tegak lurus dari titik H garis AC.
5. Perhatikan segitiga DHI. Berapa panjang HI?
Jarak titik terhadap bidang
6. Perhatikan kubus ABCD.EFGH di atas. Kubus di atas miliki panjang sisi 21 cm. Berapa jarak titik E terhadap bidang BGD? (untuk mengerjakannya, geser bangun sehingga terbentuk perbandingan panjang diagonal ruang)