Aprender GeoGebra con arte
Taller organizado para las IV Jornadas de Educación Matemática en Aragón[url] https://sites.google.com/site/ijemaragon/home[/url]
Table of Contents
- Introducción
- ¿Qué es GeoGebra?
- Algunas técnicas
- Deslizadores
- ¿Qué es un deslizador?
- Un punto sobre una función
- Área de un trapecio
- Color dinámico
- ¿Qué es el color dinámico?
- Un punto de color
- Listas y secuencias
- ¿Qué es una lista?
- Polígonos
- Diana
- GeoGebra con mucho arte
- Semitaza gigante volante, con anexo inexplicable de cinco metros de longitud
- Composición Aritmética. Theo Doesburg
- Mosaicos
- Rectángulos aleatorios
- Rosetón con Spline
- Rectángulos aleatorios coloridos
¿Qué es GeoGebra?
GeoGebra es un software de matemáticas para todo nivel educativo. Reúne dinámicamente geometría, álgebra, estadística y cálculo en registros gráficos, de análisis y de organización en hojas de cálculo.[br][br]GeoGebra, con su libre agilidad de uso, congrega a una comunidad vital y en crecimiento.[br][br]En todo el mundo, millones de entusiastas lo adoptan y comparten diseños y aplicaciones de GeoGebra. Dinamiza el estudio.[br][br]Armonizando lo experimental y lo conceptual para experimentar una organización didáctica y disciplinar que cruza matemática, ciencias, ingeniería y tecnología (STEM: Science Technology Engineering & Mathematics). La comunidad que congrega lo extiende como recurso mundial, ¡potente e innovador para la cuestión clave y clásica de la enseñanza y el aprendizaje!
¿Conoces GeoGebra?
Define tu nivel de conocimiento
¿Qué version de GeoGebra sueles usar?
¿Qué es un deslizador?
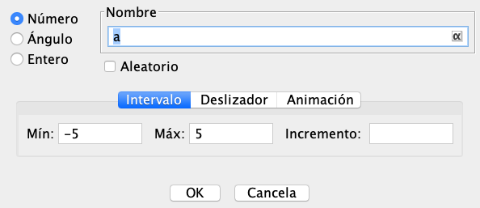
La herramienta deslizador es una de las peculiaridades de Geogebra.[br][br]Pero, ¿qué es un deslizador? Es una representación gráfica de un parámetro: numérico o angular.[br]Para insertar un deslizador hacemos clic en la herramienta [icon]/images/ggb/toolbar/mode_slider.png[/icon] y elegimos un lugar en la Vista Gráfica donde colocarlo haciendo clic de nuevo. Nos aparecerá la siguiente ventana:
En ella podemos elegir el nombre de nuestro deslizador, el tipo de parámetro que queremos, número o ángulo, el rango de variación de dicho parámetro y el incremento.[br][br]En la pestaña Deslizador podemos elegir el tipo de orientación vertical u horizontal así como su longitud.[br][br]En la pestaña Animación podemos controlar la velocidad y el tipo de movimiento: oscilante, incremento, decremento.[br][br]Al hacer clic sobre "OK" aparecerá el deslizador.
Escribe una función introduciendo el deslizador k
¿Qué es el color dinámico?
Dos de las novedades más llamativas de GeoGebra son el rastro y color dinámico. El primero de ellos nos permite dejar la huella de un objeto allá por donde pasa y el segundo nos permite cambiar el color del objeto de forma dinámica.[br][br]En la pestaña propiedades de un objeto podemos encontrar ambas posibilidades, en la pestaña básico encontraremos la opción para activar el rastro y en la pestaña Avanzado la opción para cambiar el color. Antes de adentrarnos en el color dinámico necesitaremos algunas nociones “informáticas”.[br][br]Un píxel, acrónimo “pix” de picture y “el” de element, consiste en la unidad más pequeña de información que compone una imagen. Las pantallas gráficas muestran imágenes dividiendo la pantalla en miles (o millones) de pixeles, dispuestos en filas y columnas. Los pixeles están tan juntos que parece que estén conectados.Un píxel se compone realmente de tres puntos, uno rojo, uno azul, y uno verde. Idealmente, los tres puntos convergen en el mismo pixel. Cada píxel se codifica mediante un conjunto de bits de longitud determinada, denominada profundidad de color, por ejemplo, en modo color de 8 bits permite mostrar 2[sup]8 [/sup]colores diferentes o gamas de gris.[br][br]A la hora de codificar los bits, es necesario definir que modelo de color se va usar. El modelo más común es el RGB, (Red-Rojo, Green-Verde, Blue-Azul), pero existen otros como CMYK o sRGB. El modelo de color RGB permite crear un color compuesto por los tres colores primarios según el sistema de mezcla aditiva. De esta forma, según la cantidad de cada uno de ellos que se use en cada píxel se obtendrá el resultado del color final del mismo.
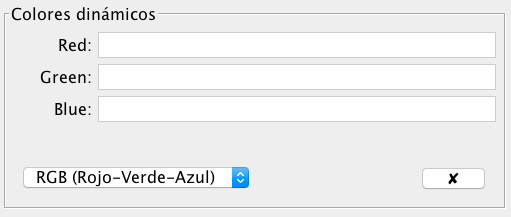
El modelo RGB asigna una valor de intensidad a cada píxel que oscila entre 0 (negro o sin intensidad) y 255 (blanco o máxima intensidad) para cada uno de los tres colores. Pudiendo obtener toda la gama desde 0 hasta 255.En la pestaña Avanzado de las propiedades de un objeto encontramos la opción de modificar la cantidad de rojo, verde y azul.[br][br]Inicialmente los tres campos aparecen vacíos. A la hora de introducir valores es conveniente tener en cuenta que GeoGebra no asigna un valor entre 0 y 255 sino un valor entre 0 y 1, donde cero es sin intensidad y 1 es máxima intensidad del color.[br][br]La verdadera potencia del color dinámico de GeoGebra reside en que en los campos Red, Green y Blue no solo podemos poner un valor fijo sino un valor variable.
¿Qué es una lista?
Las listas constituyen otra de las potencialidades de GeoGebra. Una lista es un conjunto de datos que representaremos mediante llaves separando sus elementos por comas.[br][br][center][code]l2={-2,3,5,2,-1}[/code][/center][br]Lo interesante es la naturaleza de los datos que puedo usar en una lista, ya que GeoGebra permite usar cualquier dato u objeto.[br][br][center][code]l2={(0,1), (0,2),(0,3),(0,4)}[/code] Lista de puntos[/center][br][center][code]l3={x, x^2,x^3,x^4} [/code]Lista de funciones [/center]
[code][/code]Para generar listas podemos usar el comando secuencia[br][br][b][center]Secuencia(< Expresión >,< Variable k >,< Valor inicial a >,< Valor final b >,< incremento > )[/center][/b][br][br]Para generar las lista anteriores hemos escrito:[br][br][center][code]l2=Secuencia((0,k),k,1,4)[/code][/center][br][center][code]l3=Secuencia(x^k,k,1,4)[br][/code][/center][br]Ambas listas generan la visualización de sus elementos.
Escribe en la barra de entrada la definición de la lista l2 y l3.
Semitaza gigante volante, con anexo inexplicable de cinco metros de longitud
El cuadro “[b]Semitaza gigante volante, con anexo inexplicable de cinco metros de longitud[/b]“ de Salvador Dalí tiene unas dimensiones muy particulares, es un rectángulo de 50x31 cm. Al hacer el cociente 50/31 obtenemos 1,6129... que casualmente es el número de oro. [br][br]Pintado durante los años 1944 y 1945 muestra la belleza y armonía de los rectángulos áurea. Dalí era un gran conocedor de está proporción como se puede apreciar en este cuadro.
[size=150][size=200]Construcción[br][/size][/size][list][*]Escribimos en la barra de entrada: fi=(1+sqrt(5))/2.[/*][*]Dibujamos un punto A.[/*][*]Dibujamos un punto B escribiendo en la barra de entrada: B=A + (6,0)[/*][*]Dibujamos un punto C escribiendo en la barra de entrada: C= A + (0, distancia(A,B) fi))Insertamos la imagen del cuadro colocando los puntos A, B y C como Esquina 1, Esquina 2 y Esquina 3.[/*][*]Dibujamos el punto D que nos falta para obtener el primer rectángulo áureo.[/*][*]Añadimos un deslizador para controlar la opacidad de la imagen. Establecemos su valor mínimo en 0 y su valor máximo en 1. Y se lo asignamos a la propiedad opacidad de la imagen. Lo establecemos a 0.[/*][*]Dibujamos el rectángulo A,B,D,C.[/*][*]A continuación vamos dibujando los cuadrados que extraemos para obtener rectángulos áureos.[/*][*]Cuando ya tenemos todos los cuadrados podemos dibujar la espiral.[/*][*]Por último, podemos añadir unas casillas de verificación para resaltar los elementos que nos interesen, por ejemplo, los cuadrados, los rectángulos áurea y la espiral.[br][/*][/list]