An excellent reference is '[url=https://books.google.be/books/about/The_Parthenon_s_Main_Design_Proportion_a.html?id=4GlhNAAACAAJ&hl=en&output=html_text&redir_esc=y]The Parthenon's Main Design Proportion and Its Meaning[/url]', the often cited doctoral script by Anne Bulckens on the proportions of the Parthenon.[br]A summary of the findings you can read in an article by Jay Kappraf.

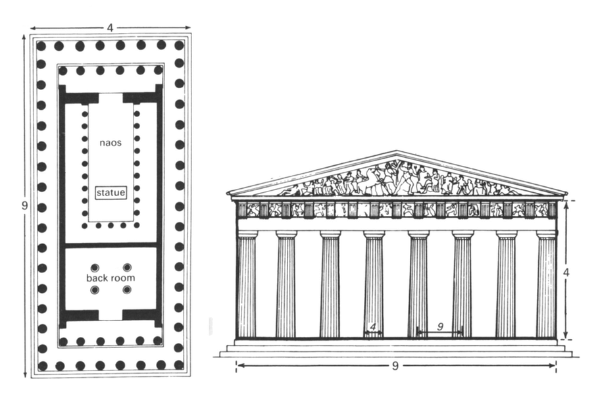
Net zoals anderen voor haar vindt Anne Bulckens in het Parthenon de verhouding 9 : 4 terug, zowel in de afmetingen van het grondplan als in die van de gevelopstand. [br]De 9 : 4 rechthoek wordt niet getekend op een foto, maar een tekening op basis van opmetingen.[br][list][*]De horizontale afstand is de breedte van het [url=https://nl.wikipedia.org/wiki/Stylobaat]stylobaat[/url].[br][/*][*]De verticale afmeting is de hoogte van de kolommen plus de entablatuur of [url=https://nl.wikipedia.org/wiki/Hoofdgestel]hoofdgestel[/url].[/*][/list][br]Kijk niettemin in onderstaand applet of je toch op een of andere manier je een gulden rechthoek terugvindt in de tekening van de gevel en welke horizontale en verticale lijnen je hiervoor moet aannemen.

Apart of the outer dimensions of the Parthenon Anne Bulckens tried to find an underlying scheme of proportions. [br]She discovered a single module of 857.6 mm, the average width of a ‘theoretic triglyph’. This matches with the writings of Vitrivius 4 centuries later in his 'de Architectura', the only remaining treatise of this size from Classic Antiquity.[br]If you divide this module by 2.5 you get a ‘Parthenonfoot’. Dividing this into 16 equal parts, you get a so called dactylys (D). The noce thing is that all dimensions in the Parthenon can be expresses as multiples of this dactylus. [br]In the picture above the dimensions of the front are written in dactyli (D).

Anne Bulckens also points to math and Pythagorean numerology.[br]The proportion 9 : 4 might be the most visible, probably the fundamental proportion is 3:2 with 6, the geometrical mean of 9 and 4 as the essential key.[br]Using the three numbers you get 9 : 6 :: 6 : 4 which is two times the proportion 3 : 2. For Pythagoras the quint proportion forms is the basis to form his tonal system.[br]More details on these proportions are in the article by Jay Kapraff.

For us this 9 : 6 :: 6 4 seems far-fetched. We look at things and measure distances trying to find laws. the Pythagoreans do the reverse. In their ontology numbers and their relations are the core of things. In this geometry and music are visible and audible expressions of these proportions. E.g. the number 10 is represented as a triangle number in the form of a four (tetraktys).

In this 10 is the combination of the first 4 numbers and symbol of the cosmos.[br]1 stands for a point, 2 for line, 3 for a flat plane and 4 for space.[br]At the same time the mutual relationships match with the natural harmonics in music:[br][list][*]octave 1 : 2[/*][*]quint 2 : 3[/*][*]quart 3 : 4[/*][/list]In Pythagorean thinking irrational numbers didn't have a place. The annoying [math]\sqrt{2}[/math] could be fit in as the diagonal of a square with side 1, being itself the side of a square with a surface twice the one as the square with side 1.[br]In this ontology there's no place for [math]\frac{\sqrt{5}-1}{2}[/math], not even to think that this number would be an esthetic ideal.[br]Only in the environement of Plato, by students as Euxodus (ca. 410 - 350 BC.), so after the construction of the Parthenon, proportionality was extended to relations between sizes that couldn't be rationally measurable.

Were we look at symmetry as e.g. an ABA scheme, in Antiquity symmetry meant an inner coherence of proportions, a modular system in which one could fit all parts in the whole. So the finding of the dactylus in the dimensions of the Parthenon isn't mathematical hocus-pocus but logic itself.[br]It's about the being of things, not about an esthetical criterion that, if used, ensures that people like the temple. [br]If (in its old meaning) symmetry coincides with beauty is a dicussion in which the meaning of different pholosophers differ. Again this confirms that, looking at a Greek temple, we don't have to search for a criterion of beauty as the fundamental desinging principle.