[justify][size=100]Platão (c. 427 a.C. – 347 a.C.) foi um dos mais importantes filósofos da Antiguidade e um dos principais fundadores do pensamento ocidental. Discípulo de Sócrates e mestre de Aristóteles, suas ideias influenciaram profundamente a filosofia, a política e a educação. Ele fundou a Academia de Atenas, a primeira instituição de ensino superior do mundo ocidental, onde buscou fomentar o estudo e a reflexão crítica.[br][br]Na área filosófica, Platão é mais conhecido por sua teoria das ideias ou formas, segundo a qual a realidade sensível é uma cópia imperfeita de um mundo ideal, imutável e eterno. Essa concepção moldou gerações de pensadores e ajudou a estruturar a metafísica e a epistemologia ocidentais.[br][br]No âmbito da matemática, Platão também teve relevância ao enfatizar a importância dos estudos matemáticos na formação do pensamento filosófico. Ele considerava a matemática um caminho para se aproximar da verdade, devido à sua natureza abstrata e imutável. Os sólidos platônicos, conhecidos muito antes de Platão pelos pitagóricos e babilônios, ganharam uma nova perspectiva na filosofia de Platão. Esses cinco sólidos são chamados de "platônicos" porque Platão os apresentou em seu diálogo Timeu, onde esboça uma cosmologia usando a metáfora da geometria plana e dos sólidos. Platão associou cada um desses cinco poliedros a um dos elementos fundamentais da natureza: fogo, terra, ar, água e o cosmos. Ele acreditava que o universo tinha sido formado a partir dessas formas geométricas, criando uma simetria perfeita entre a matemática e o mundo natural.[/size][/justify]

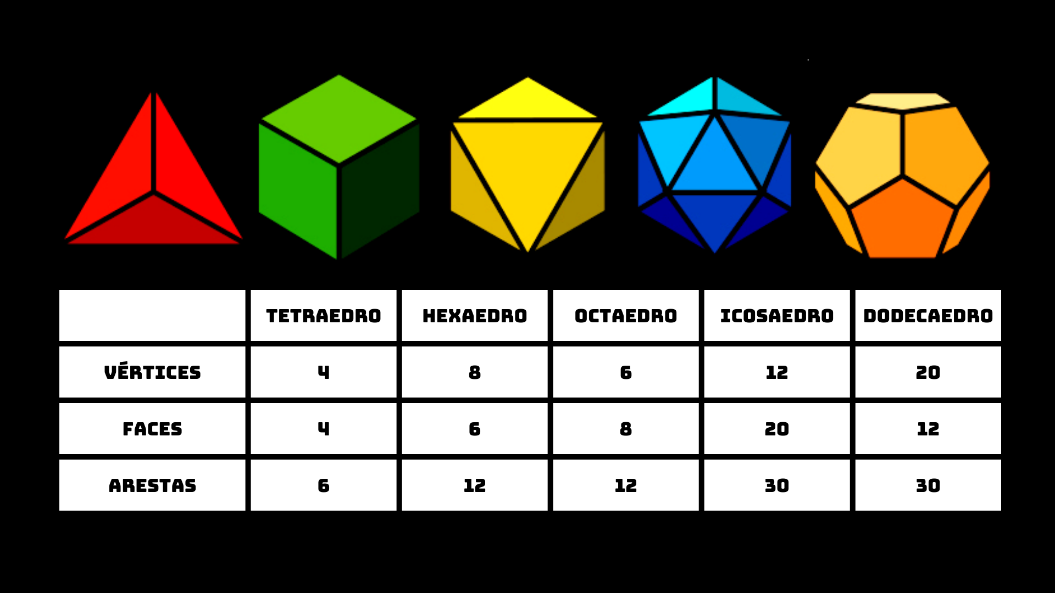
[justify]Os sólidos platónicos são poliedros regulares que satisfazem a relação de Euler: [br][br][b][size=150][color=#a64d79]Vértices + Faces = 2 + Arestas[/color][/size][/b][br][br]Um poliedro regular é todo poliedro convexo que possui: em todas as suas faces polígonos regulares congruentes entre si; todos os seus ângulos poliédricos são regulares e congruentes entre si e; de cada um de seus vértices partem o mesmo número de arestas.[/justify]