Problemas calendario matemático
Problemas calendario matemático
Table of Contents
- 07/06/2020
- pirámide cuadrangular seccionada
- 11/06/2020
- Volumen del sólido ABCDEF
- 13/06/2020
- Volúmenes cilindro y cubo inscrito
- 16/06/2020
- Volúmenes cubo y cilindro inscrito
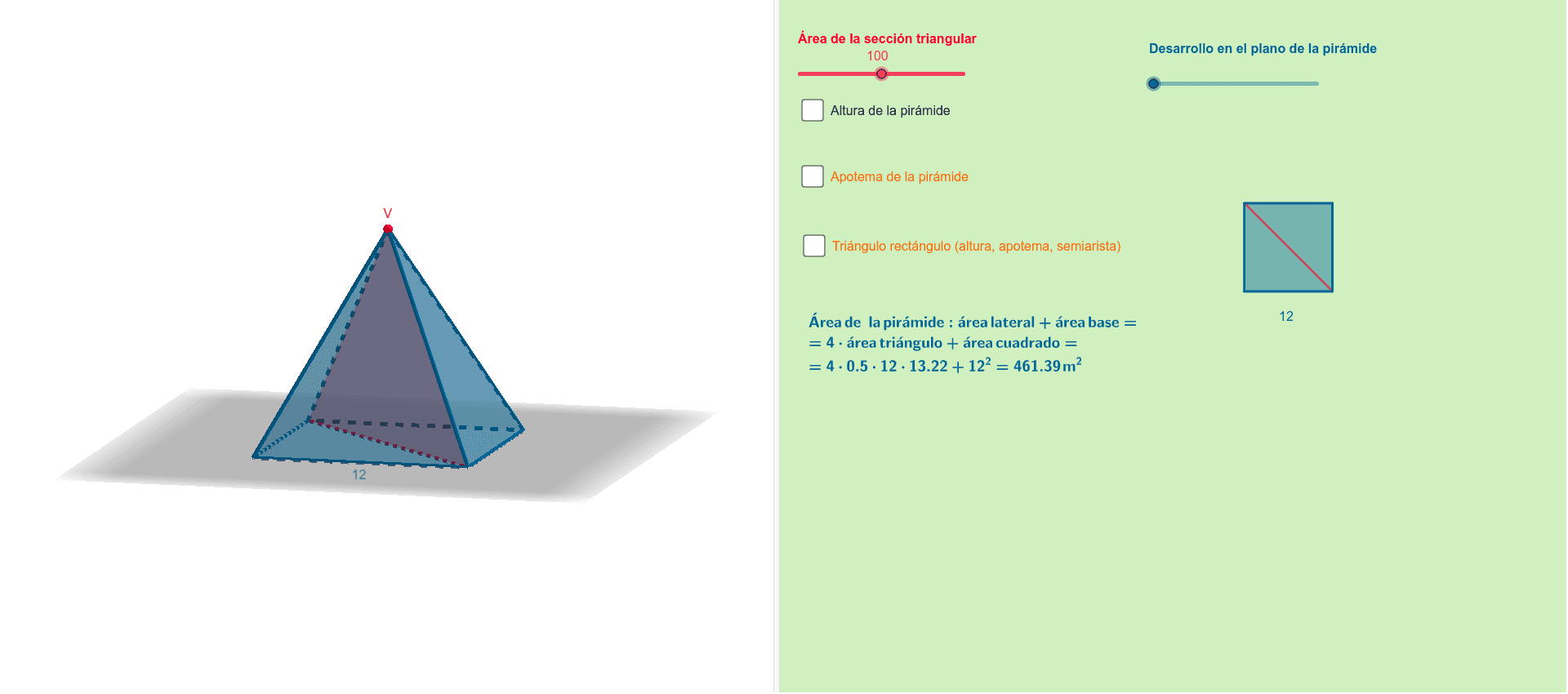
pirámide cuadrangular seccionada
Problema calendario matemático 7 de junio de 2020
El área de la figura que resulta de cortar una pirámide cuadrangular regular por dos aristas laterales opuestas es igual a 100 [math]m^2[/math] y la arista de la base es de 12 m. Determinar el área total de la pirámide.
Solución:
El problema de calcular el área de la pirámide, conocida su arista básica, se reduce a hallar la apotema de la pirámide. [br][br]La [b]apotema de la pirámide [/b]se calcula aplicando el teorema de Pitágoras en el triángulo rectángulo de hipotenusa la apotema y catetos, la altura de la pirámide y la arista partida por dos. [br][br]Necesitamos, por tanto, hallar la [b]altura de la pirámide[/b] para resolver el problema. Para ello, tendremos en cuenta que es la altura de un triángulo isósceles del que conocemos el área y la el lado desigual (diagonal del cuadrado base de la pirámide).[br][br]Nota: La resolución permite variar el área de la sección mediante el deslizador "área de la sección triangular".
Volumen del sólido ABCDEF
Problema calendario matemático 11 de junio de 2020
En la figura, ABCD es un cuadrado de lado [math]6\sqrt{2}[/math]. EF es paralelo al cuadrado y tiene longitud [math]12\sqrt{2}[/math]. Las caras BCF y ADE son triángulos equiláteros. Calcular el volumen del sólido ABCDEF.
Solución
Completamos el volumen de la figura con dos pirámides y así obtenemos un prisma de base triangular. El enunciado nos proporciona datos suficientes para hallar los volúmenes del prisma y las pirámides. Mediante una resta, se obtiene el volumen del sólido ABCDEF.[br][br]NOTA:El valor exacto del volumen del sólido es de 388. [br]Se obtiene el resultado mostrado debido a errores de aproximación[br]en los cálculos intermedios del volumen del prisma.
Volúmenes cilindro y cubo inscrito
Problema calendario matemático 13 de junio de 2020
Un cilindro de 1 m de diámetro está circunscrito en un cubo. Calcular el volumen de los dos cuerpos.
Nota:
Se ha generalizado el problema y la solución al caso de un cilindro de diámetro "d". El valor del diámetro se varía con el deslizador que aparece en la vista gráfica.
Volúmenes cubo y cilindro inscrito
Problema calendario matemático 16 de junio de 2020
Un cubo de arista a 1 m está circunscrito a un cilindro. Calcular el volumen de los dos sólido.
Nota
Se ha generalizado el problema y la solución al caso de un cubo de arista "a". El valor de la arista se varía con el deslizador que aparece en la vista gráfica.