MA 36

Ana Paula da Silva Gueiros Duarte, Jun 14, 2024

Livro criado na disciplina de MA 36 - Recursos Computacionais no Ensino da Matemática.

Table of Contents

  1. Geometria Plana - Aula 1
    1. Mediatriz
    2. Retas Perpendiculares
    3. Retas Paralelas
    4. Divisão de um segmento por partes iguais
    5. Ângulo
    6. Bissetriz
  2. Geometria Plana - Aula 2
    1. Arco Capaz
    2. Triângulo
    3. Retas Tangentes

1.

Geometria Plana - Aula 1

Referência MUNIZ NETO, Antonio Caminha. Geometria/Antonio Caminha Muniz Neto. - 2. ed. - Rio de Janeiro, RJ: SBM - Sociedade Brasileira de Matemática, 2022.

  • 1. Mediatriz
  • 2. Retas Perpendiculares
  • 3. Retas Paralelas
  • 4. Divisão de um segmento por partes iguais
  • 5. Ângulo
  • 6. Bissetriz

1.1.

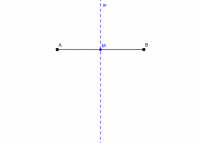
Mediatriz

Definição
Dados os pontos A e B no plano, a mediatriz do segmento AB é o lugar geométrico dos pontos do plano que equidistam de A e de B,
Problema:
Trace a mediatriz de um segmento AB dado.
Solução:
1. Dado o segmento AB e usando o compasso com uma abertura maior do que a metade do segmento dado, trace duas circunferências de mesmo raio com centros em A e em B.[br][br]2. Note que essas duas circunferências se intersectam em dois pontos, nomeados de pontos D e E.[br][br]3. Esses pontos formam a reta[b][i] r[/i][/b] suporte à mediatriz do segmento AB.
Mediatriz
– Ana Paula da Silva Gueiros Duarte, Ana_Paula_da_Silva_Gueiros_Duarte

1.2.

–

1.3.

–

1.4.

–

1.5.

–

1.6.

–

2.

Geometria Plana - Aula 2

Referência MUNIZ NETO, Antonio Caminha. Geometria/Antonio Caminha Muniz Neto. - 2. ed. - Rio de Janeiro, RJ: SBM - Sociedade Brasileira de Matemática, 2022.

  • 1. Arco Capaz
  • 2. Triângulo
  • 3. Retas Tangentes

2.1.

Arco Capaz

Definição
Dados um segmento BC e um ângulo [math]\alpha[/math], com [math]0^\circ<\alpha<180^\circ[/math], o lugar geométrico dos pontos A do plano tais que [math]BÂC=\alpha[/math] é a reunião de dois arcos de círculo, simétricos em relação à reta BC e tendo os pontos B e C em comum. Tais arcos são os arcos capazes de [math]\alpha[/math] em relação a BC.
Problema
Se um segmento de reta AB e um ângulo [math]\alpha[/math] são dados, construa o arco capaz.
Solução
Arco capaz é o lugar geométrico dos pontos que visualizam um segmento AB e um ângulo [math]\beta[/math].[br][br]1. Use o compasso para transportar o ângulo [math]\beta[/math] para abaixo do segmento AB, definindo o ponto F, de modo que [math]\beta[/math]=[math]FÂB[/math]. [br][br]2. Trace uma mediatriz AB. [br][br]3. Levante a perpendicular de AF por A e marque a intersecção com t, determinada O.[br][br]4. Com o compasso centrado em O use o compasso (arco circular) no Geogebra [icon]/images/ggb/toolbar/mode_circlesector3.png[/icon] e trace o arco capaz. [br][br]5. Sobre o arco capaz defina um ponto qualquer I e verifique que o ângulo [math]AÎB[/math] é igual ao ângulo dado. Deslize o ponto I sobre o arco e verifique que o ângulo se mantem o mesmo.
Arco Capaz
– Ana Paula da Silva Gueiros Duarte

2.2.

–

2.3.

–

Information