Poncelet's Closure Theorem
Table of Contents
- Introduction
- Conic sections
- Poncelet's Closure Theorem
- Structure
- Note
- Euler's totient function
- Poncelet's Porism for Two Circles
- n=3
- n=4
- n=6
- All Other n
- n=5
- n=7
- n=8
- Statement
- Future
- Future Development
- Acknowledgments
- Bibliography
- Poncelet's closure theorem
- Euler's totient function
- Conic Section
- Poncelet's Porism for 2 circles
- PonceletsCLosureTheorem
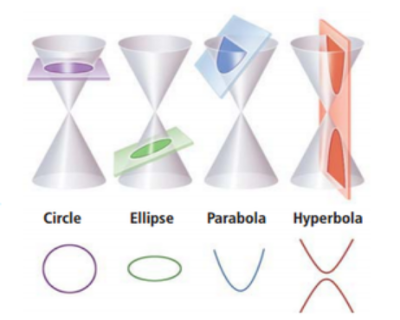
Conic sections
The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone. For a plane perpendicular to the axis of the cone, a circle is produced. For a plane that is not perpendicular to the axis and that [url=http://mathworld.wolfram.com/Intersection.html]i[/url]ntersects only a single nappe, the curve produced is either an ellipse or a parabola. The curve produced by a plane intersecting both nappes is a hyperbola.
n=3
Proof
Let [math]OI=d[/math][br][math]AI=1-d[/math] and [math]AE=1+r-d[/math][br]Phitagoras' theorem for [math]\text{\triangle}AIF[/math][br][math]\Longrightarrow AI^2=AF^2+FI^2[/math][br] [math]\left(1-d\right)^2=AF^2+r^2[/math][br] [math]AF^2=\left(1-d\right)^2_{ }-r^2[/math][br] we construct [math]CL[/math]- angle bisector[br][math]\angle CAL=90^{\circ}[/math] and [math]\angle CEI[/math]([math]CA[/math]- tangent)[br][math]\angle LMA=\angle LCA=\frac{\widehat{AL} }{2}[/math][br][math]\Longrightarrow\text{\triangle}CEI\sim\text{\triangle}MAL[/math][br] [math]\frac{CE}{MA}=\frac{EI}{AL}=\frac{IC}{LM}[/math][br] [math]\frac{CE}{MA}=\frac{r}{AL}=\frac{IC}{2}[/math][br] [math]AL.IC=2r[/math][br][math]\angle AIL[/math]- exterior angle[math]\text{ \triangle}CAI[/math] [br][math]\Longrightarrow\angle AIL=\angle CAI+\angle ICA[/math][br] [math]CL[/math]-angle bisector[br][math]\Longrightarrow\angle BCL=\angle ACL[/math][br] [math]\angle BCL=\angle BAL=\frac{\widehat{BL}}{2}[/math][br]and [math]AP[/math]- angle bisector[br][math]\Longrightarrow\angle BAI=\angle CAI[/math][br][math]\Longrightarrow\angle IAB+\angle BAL=\angle AIL=\angle IAL[/math][br][math]\angle IAL+\angle IAB+\angle BAL=[/math][br] [math]=\angle IAC+\angle BCL=[/math][br] [math]=\angle IAC+\angle ICA=\angle AIL[/math][br][math]\Longrightarrow IL.IC=2r[/math][br] and [math]AP[/math] and [math]CL[/math]- chords[br][math]\Longrightarrow IL.IC=AI.PI[/math][br] [math]\left(1-d\right)\left(1+d\right)=2r[/math][br] [math]1-d^2=2r[/math][br] [math]d=\sqrt{1-2r}[/math][br]In conclusion it can be said that[math]d=\sqrt{1-2r}[/math] or [math]r=\frac{1-d^2}{2}[/math]
Poncelet's closure theorem for n=3
Note:
It also follows from the Euler's theorem: the distance [math]d[/math] between the cirdumcentre and incentre of a triangle is given by [math]d^2=R\left(R-2r\right)[/math] or equivalently [math]\frac{1}{R-d}+\frac{1}{R+d}=\frac{1}{r}[/math].
n=5
[math]r\left(1-d\right)=\left(1+d\right)\sqrt{\left(\left(1-r+d\right)\left(1-r-d\right)\right)}+\left(1+d\right)\sqrt{\left(1-r-d\right)2}[/math]
Future Development
In future, an attempt will be made to summarize the theorem for two circles, and studies for other conic sections will be investigated:[br][math]\bullet[/math] circumcircle and inscribed ellipse[br][math]\bullet[/math] incircle and circumscribed ellipse[br][math]\bullet[/math] two ellipses, etc.