Drone Data
Antidote Testing Data
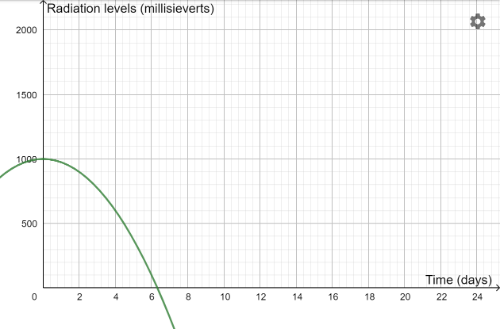
We have been testing different antidotes for the radiation pollution.[br]The following graph about the first antidote we created, shows the rate at which it removes radiation from the atmosphere, it models a negative quadratic function.[br]
Analysing the graph:
What are the coordinates of the y-intercept?
What does this mean? (Considering the first data point is at the beginning before any days have passed with the antidote present)
Millisieverts - Radiation level readings
Millisieverts (mSv) are a unit of measure for radiation levels.[br]1000 mSv is a dangerous level for living beings, it can cause sickness but that level of radiation would not be fatal.[br]100 mSv is the lowest annual dose which can cause health problems so still not ideal but we are aiming to reduce the levels to below 100.
The data models a quadratic function with the equation y=1000-25x[math]^{^2}[/math][br]Complete the following table of values to find coordinates of some of the points on the graph:[br][br]Example:[br]1[math]^2[/math]=1[br]1x25=25[br]1000-25=975[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABBMAAACeCAYAAABgp0JIAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAABBHSURBVHhe7d3tbhNHGwZgOxxVER8CqZD0eFAISvoPlAR6PA3wo4gPcVYlL7fryTtZ1rHH6zh2cl3SCpM4wRKPZnfufWZ2fP7TCAAAAGBBO9M/AQAAABYiTAAAAACaCBMAAACAJsIEAAAAoIkwAQAAAGgiTAAAAACaCBMAAACAJsIEAAAAoIkwAQAAAGgiTAAAAACaCBMAAACAJsIEAAAAoIkwAQAAAGgiTAAAAACaCBMAAACAJuPzn6avm7w7PZ6+AgAAALbRi/2D0Xg8nv5tcToTAAAAgCaDOxOWTTFADTGE+mEoNcRQaoih1BBDqB+G+uvtyShxwLI1pDMBAAAAaCJMAAAAAJoIEwAAAIAmwgQAAACgiTABAAAAaCJMAAAAAJoIEwAAAIAmwgQAAACgiTABAAAAaCJMAAAAAJoIEwAAAIAmwgQAAACgiTABAAAAaCJMAAAAAJoIEwAAAIAmwgQAAACgiTABAAAAaCJM4FZ5+/btaGdnZzQejyfHjx8/pt+B2VI3u7u7k6PUTo6Tk5PR169fR+fn59N3wq++ffv2y9iT4/nz55OaUkMsY29v71I9ffnyRR3xi+64M+9QR8zjnEYLYQK3Ri68Xr58aYBjYTlh5sSYuvnw4cPkqL169Wr06NEjJ096pX5ysfXw4cPesefjx4+Tmio1JNxkUTmfvX//fvq3/7x588YYxCUZg2BVWs5pxiIKYQJbrwx+3QsvuErqJifEOkB49uzZJHnvygnUyZOubk0cHx+PTk9PJ0e3jlJDudOjhpgnY1M32IRFlHPYVceDBw8md5mhVq6JZp3T+s5rEMIEtlru3iRBLYNfTqSwiO/fv09f/XfCzF3jXMAnlEo9pROhe+I0GaSW+shSmLQNp34ODg5G+/v7kyN1lBqqL9rT6aJ+mKfuQPj8+bOJHwvJ9c/Z2dlk7LnqyM0XqCVIePz48aVr6X///ffSOa2c18r1kXGJwojC1qrbQDPw5YL+zz//NMCxkPv371/UTdr5unWTuzdHR0cmg8yUC/fUTgLNvnEnNZSwof5eLtrUELMksCxdCQk5nc+A65YAsyzDK6HUVaGT7hZqNx4m5MIqBVmOXHjNutDqvtcF2d1WLrjKwJcLelhUToYJo2ZNBKNvMggtcjcHFpU7gbm2yXkttWPsAa5T5lb1sqp5QQJ03Wi1JIHvTgBz569vo7MUu8kitdJerG0PgG2Xbrty7XN4eChIAK5dveTTsiqWcWMzsIQDaQ8ta02zsUcp4O6OxX1BQlJ77rbctbnqrjLATcv5C+ap7w7m+kYbMbAOpRsqjDss48bChCRh9a6ydStodr2ulSChBA/x9OnTyZ8A1+nTp08XJ1ohJq3qcNwkkVnqOtFmDKyDsJtVuLGzVdkVtL6o6nvkSNr+Ii3t5SIsJ9y+DdMAVq1eS/jkyRPjDgurN4kNrev0sekiq1AeP1sfWTacCWMJqmCWcrMk9ZLaSaCZsagcmaOli1wt0bVR0Xd9oV4GwZxgU+A2IgLWLeNQzThEn3LhXh+5EKuDhKxFtSyLPjZdZFWy71hutpXj0aNHk3En49FVG5xzN9X7JcS9e/cm9ZLa6dZKwqqMVamldIqrJYqN7aNLa3EGwd9///2XDgaAdajXElriQJ/cxUmd1Bfw9YVY6ibP6875zHmMLpsusi4JGnZ3dy+WC0Otu8Q8XVLpRMjR7Rx//PixMIELGxUm9O2bkJMrwLrVF/lhHTN9svzuKjmX5W5PLsZcxFOz6SJDpWZylzidvBlfcs4qR76Wo66pjEc5txmL6JMAoexPl5A887IcuanbrSV1RLHRV8baQoGbkDb1eq8Ej0viKt2L+BzduzklVNAeSmHTRVYhgUJfEFW+nvEpHQlFxiL7KNBVllnNmnellrJUpnyv3PSFjTtz9W3CCLAupW29XGglqRdq0mrW3Zzuo4+5m+rA0qaLXLeEVXWNddfKwyLqDnIoNipMqFv+wmAHrFPGoKxtL5M9G6IxlLs59KkDy3j37t2lDTzL8fr164v3pXbq7wmlaFHfrKsfeQzL0uFCbFSY0L1jY7AD1qUvSNB6zCrcv39/+uo/JoLUujvw10d9gyXq96brRR2xKI82pqs+Nwm6WdbGXCVnPVdaQq1NBtZNkMB1SncCrFrqyvUSi3KDji7nJlZhI66Uy/KGsja5tGJJyYDrJkjguqXGat1OBe6evk07+456z42MTXnMaPmeMYpl6VKgz7yuue65TKBJ3PiZKIWZAGHW2mTtoMB1ESSwDt0lfC7AgHXKtXS9ZMZeQBQte2nU5zIbx1Ks/Yo5F+8pvqTtJUiIo6Oji6KsE9MUdpH3ZzmEdYLAUIIEhsjFec5HeQTkVeejPIs7S/gKF2DAKuQclvPVvMfNZqyqN/zMuQ6Kw8PDi3NSOsJzzkrnVFf3XKbDjmL8c3BZalb+7vR48ueL/YOmC6MMatk4qJaBsHunJgNk+Wj5fr6XXY2TrKbIXYxtv2VrqMiJtPvEj3/++edS+p4L93py+Ntvv7kreEsMrZ/uiTEXWIv8noSd7urcDkNqqO8C/enTp5d+T3fHfoHV7TN0HJqnDj3Vz+20bA31BeL1GNS9Hgo1dPusYgzqux6qa6l7Lsv+dh6ZfXv89fZk8v+7bA3deJiQgk0Bd39Ht7CLvuCB7TR0AKwDpxZZc+pEuv1uqn7CifR2GFJDuZAvAfciEmzm3KdmbpdVXMhfRZhw+y1bQ90wYR5j0O20qjHojz/+mIwv87j+uX2GhglrPyMlKS3y7O2+ICFS0GkhLfJeQQK1ep3XonIxBlE/+7+VcYjUQM5fWeaQo288ynhTzl0u4oFVyhiUTt0s/Z03BuV9ubtsDGKWv//+e1JLqaNuLdV1lABLHVFbe2cCFGqIIdQPQ6khhlJDDKWGGEL9MNTWdSYAAAAA202YAAAAADQRJgAAAABNhAkAAABAE2ECAAAA0ESYAAAAADQRJgAAAABNhAkAAABAE2ECAAAA0ESYAAAAADQRJgAAAABNhAkAAABAE2ECAAAA0ESYAAAAADQRJgAAAABNhAkAAABAE2ECAAAA0ESYAAAAADQZn/80fd3k3enx9BUAAACwjV7sH4zG4/H0b4vTmQAAAAA0GdyZsGyKAWqIIdQPQ6khhlJDDKWGGEL9MNRfb09GiQOWrSGdCQAAAEATYQIAAADQRJgAAAAANBEmAAAAAE2ECQAAAEATYQIAAADQRJgAAAAANBEmAAAAAE2ECQAAAEATYQIAAMCWGY/H01dwM4QJAAAAQBNhAgAAANBEmAAAAAA0ESYAAAAATYQJAAAAQBNhAgAAANBEmAAAAAA0ESZwK7x9+3a0u7s7ed5ufZycnIy+fv06Oj8/n77zV3t7e7/83KLH8+fPRz9+/Jj+pv/ks+zs7PS+v+/o+x0AAACbTJjAVitBwMuXL0cfPnyYfvX/Xr16NXr06NHo27dvMwOFvp8b4tOnT1eGFwAAANtOmMDWSpDw/v376d9Go2fPnk06EU5PTydHQoYigcKsDoV0BrQctSdPnlz6d/rkc/X9nnIcHR3N/R0AAACbRJjAVspSgrqj4Pj4eBIspENhf39/cmTpQJY+FI8fP+4NE87OziY/u+hRT/zv378/fdXv8+fPvb+jPh4+fChMAAAAtoowga1ULyVIkJAQoW9Cfnh4eOnrVy13WERCjNqDBw8EAQAAwJ1zo2FCJmaZiJXjy5cvMyd6mQTW7y3HkIkh26vuSkgXQmqhTyb7WfpQfP/+ffpqOQcHBxc1l66DWf8uAADAbXZjYULaz3M3uZY29Fnr2jMpFBwQdXdA9iOYp16KkA0Zl62jBFo1XQkAAMBddSNhQoKE3FlOJ0LWtWcTuuLNmzdXTvbq99Z3nOG6ZRPHUptZWiFIAAAA7qob60xIkFDu7D59+nT61dHo48eP01fzzdv8DiJ1Vltm34RuV4LaAwAA7rIbCRO6O9hnzfui6rXy2szvpnoi3xI+DVF3zKQrYdEnMOTnsiyjPmYt5QEAANgWN7oBY61evpAJV99kq747nM4GiGU6DVrk99chVktXQsKObNqY/UHKkeUSOzs7k5oXLAAAANtoY8KERdQ78etKuLu6yxau2rgz9vb2pq+W030CxKpqL0FDggWBAgAAsG02JkzIvgllgvbp06feyVV5+oONF0lnSj2hT6Bwenp6aTlBNvrMe7KsZojWx0GenZ1NAoIc2WA0P1uOfK3uwol5YQgAAMCm2ZgwYV7reL3EIXssrOLOMNsr3QHdQCGPfayXE5SlCYs8PnKWhBK1RbsS8r6+9+ZrCTcSHtTfm/cUEwAAgE2yMWFCJllF36Z6r1+/nvxprwSK1EzqIR0J3Ul7AoR0AKSLpduZ0DfJn6XuSljl4yDzGfLZyu9b10aSAAAAq7BReyZ027+LegO8lokgt1/qIZ0q3eUEqZeECOlQWLZe6m6YWHVHTLcb57o3kgQAAFiVjd2AsZ5Y6UpgiHqpQsuSh2yOWGpwlV0JRYIQAACAbbRRYcKTJ08uJmxlB/3SlZBJoK4ElpENPYu6xq7S7UpoeRzkorr/BgAAwLbYqDChb8KWu8NxdHQ0+RNalSUysehShXpDxHUFWcIyAABgW2xUmFC3feducmlPz0Z1JlosY29vr3mpQumGKQ4PD6+l9q57GQUAAMB12dg9E6LspO9RkHRlwp+jTMa78r3d3d2LJzmku2DROipLbIqWICvhRf7dbAg5S/ls9We/jmUUAAAA12XjwoTyRIfyqLzPnz9P/oRaliE8fPhwtLOzM+lcSRdLOTJRz/dKd0GChIQKee88megPfRxk/t179+5NajmfJY+uLJ8tn6H+bJEaz9cEZgAAwLbYuDCh3iDPpovMUtfJq1evJo+ALEc9UU8NnZ2dLVxD3a6EIV0xCcTyWRJOlM9WdyPks+UJJYIEAABg22z0ModMAhe5m8zdk0l+OhJKJ0stk/R8L0sNMplvqaHs1VEm/OkYaJ3kp2bz8+lGyGfr+3zpdkiIkG4JQQIAALCNNmqmXreYLzOR425JoJAJeeqlPhIgpAtgmfopYUCObJC4bA2Wz9b3+VLjQgQAAGCbbVSYUHa3z51bky0AAADYTBsTJpTd7dOiPmSdOgAAAHC9NiJMSJBQNs27rmf6AwAAAKux9jAhj8dLWJAuhPK8/RIkeEQeAAAAbL61hwnZGC+6z9v3iDwAAADYDmsNE9KJ0CdBwoMHDwQJAAAAsAXWGiYkMKidnJyMfvz4oSMBAAAAtsjalzmUZ+3nyJIHIQIAAABsl7WHCQAAAMB2EyYAAAAATYQJAAAAQBNhAgAAANBEmAAAAAA0ESYAAAAATYQJAAAAQBNhAgAAANBEmAAAAAA0ESYAAAAATcbnP01fN3l3ejx9BQAAAGyjF/sHo/F4PP3b4nQmAAAAAE2W7kwAAAAA7iadCQAAAEATYQIAAADQRJgAAAAANBEmAAAAAE2ECQAAAEATYQIAAADQRJgAAAAANBEmAAAAAE2ECQAAAEATYQIAAADQRJgAAAAANBEmAAAAAE2ECQAAAECD0eh/St/vDCR0dloAAAAASUVORK5CYII=[/img]
After how many days will the radiation levels fall below 100 mSv?
Use the slider to see what happens when you increase or decrease m (the coefficient of x squared)
Write down what you notice, do we want the coefficient of x squared to be more than -25 or less than -25?
What is the drop in mSv between day 2 and day 4?
We have been running further tests on this antidote and the 6 outcomes are shown in the results below. There was a mix-up though with this data. Can you match each graph with the correct quadratic equation?[br]The equations are:[br]y=1000-2x[sup]2[br][/sup]y=1000-5x[sup]2[br][/sup]y=1000-10x[sup]2[br][/sup]y=1000-25x[sup]2[br][/sup]y=1000-50x[sup]2[br][/sup]y=1000-100x[sup]2[/sup][br]
Antidote A

Antidote B
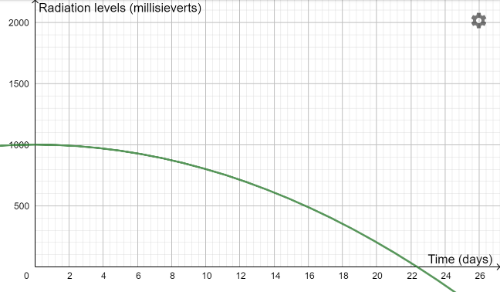
Antidote C
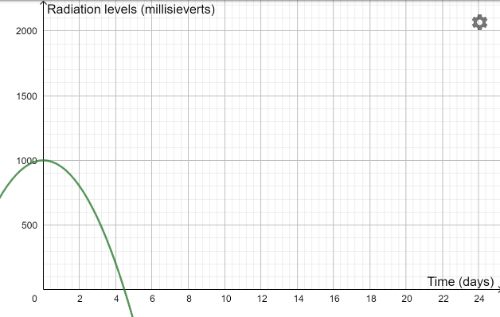
Antidote D
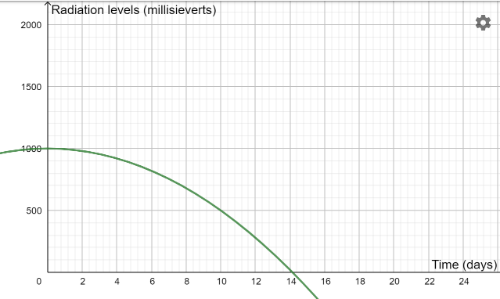
Antidote E
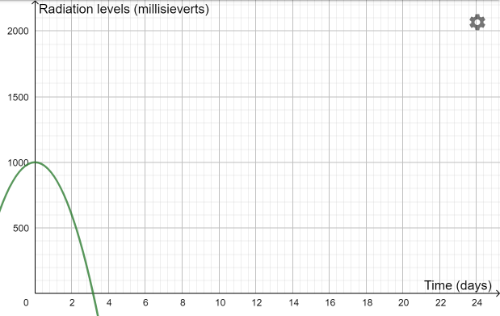
Antidote F
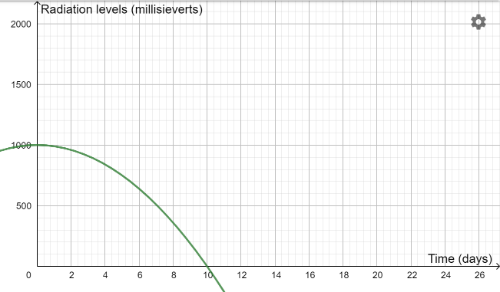
Can you match each antidote with an equation?[br][br]Here is a reminder of the equations:[br]y=1000-2x[sup]2[br][/sup]y=1000-5x[sup]2[br][/sup]y=1000-10x[sup]2[br][/sup]y=1000-25x[sup]2[br][/sup]y=1000-50x[sup]2[br][/sup]y=1000-100x[sup]2[/sup]
Which antidote would be the most successful trial, and the one we should select to use in the town?