Função Quadrática - de segundo grau .
Objetivo:
O objetivo desta aula é esclarecer aos estudantes como a função de segundo grau se apresenta algébrica e graficamente. De forma didática e prática , nosso intuito é sanar todas as dúvidas e questionamentos sobre o assunto.
O vídeo abaixo mostra alguns conceitos importantes da função:
De acordo com o vídeo acima, responda às perguntas:
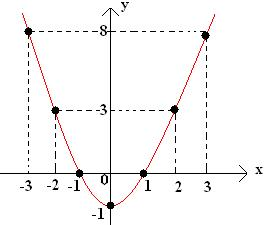
As raízes da função são os pontos que a parábola "corta":
De acordo com o gráfico abaixo, qual das opções apresenta os pontos do vértice

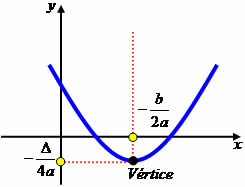
Para calcularmos as coordenadas dos pontos máximo e mínimo de uma função de segundo grau, ou seja, o vértice da parábola, precisaremos de 2 fórmulas:
Definição:
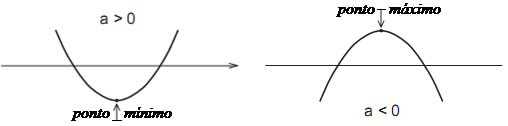
Ponto máximo: concavidade da parábola para cima ("feliz").[br]Ponto mínimo: concavidade da parábola para baixo ("triste").
Peguemos a parábola abaixo como referência e calcularemos a função:
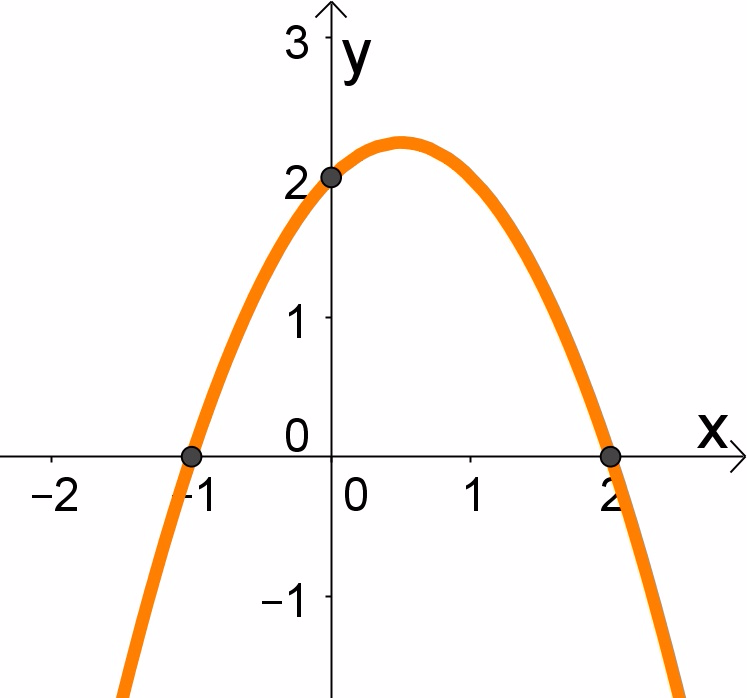
Passo 1: Identificar os pontos (-1,0) , (2,0) e (0,2).[br][br]Passo 2: Reconhecer as características dos pontos dados.[br]Exemplo: -1 e 2 estão cruzando o eixo X e, portanto são as raízes da função.[br] O ponto 2 está cortando o eixo Y e , portanto é o "c" da função. [br][br]Passo 3: Substituir os pontos na função f(x)= ax² + bx + c.[br]Exemplo: (-1,0) : 0 = a (-1)2 + b (-1) + 2, ou seja, a = b -2 e[br] (2,0): 0= a (2)2 + b (2) + 2, substituindo teremos 4(b-2) + 2b + 2 = 0.[br] No final teremos b = 1 e a=-1. [br] Ao fim desses 3 passos, chegamos à conclusão que a lei de formação da função é f(x)= -x² + x + 2.[br] [br][br]
Ao mexer o ponto "a" no quadro interativo, percebe-se que ao tornar-se negativo, a parábola fica "triste", ou seja, é decrescente.
Ao mexer o ponto "c", percebe-se que a parábola muda os locais em que a mesma cruza o eixo Y, evidenciando a teoria de que o ponto "c" cruza o eixo Y.
Exercícios:
Ao variar o botão do coeficiente "a" (azul) de -5 até 5, o que acontece com a concavidade da parábola? ( sugestão: clicar no botão "play" e observar).
Fixe o botão do coeficiente "a" (azul) no ponto 0 (zero). Qual gráfico você observa?
Achando as raízes da função:
Para acharmos as raízes da função, utilizaremos a fórmula de Bhaskara, principal método de resolução da função de segundo grau.
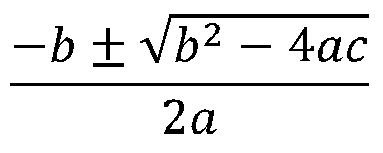
Tomando como base a função [b] f(x) = x² + 3x – 10 , identificamos a = 1, b = 3 e c = -10.[br][/b]
Assim, substituindo na fórmula de Bhaskara temos: [math]\frac{-3\pm\sqrt{3^2-4.1.-10_{ }}}{2.1}[/math]
Ao final das contas. teremos X1= 2 e X2= -5.
No gráfico abaixo, evidenciamos que as raízes cruzam o eixo X nos pontos -5 e 2, assim como na teoria apresentada.
Estudo do delta:
O Δ da função faz parte da fórmula de Bhaskara e pode ser usado para reconhecimento de alguns fatores da parábola.
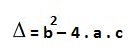
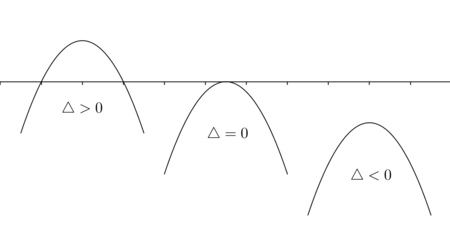
[b] Existem algumas relações entre a parábola e o delta da função de segundo grau:[/b][list][*][b]Primeira condição:[/b][b] [/b]Quando Δ > 0, a função possui duas raízes reais diferentes. A parábola interceptará o eixo x em dois pontos distintos.[/*][*][b]Segunda condição:[/b] Quando Δ = 0, a função possui uma única raiz real. A parábola tem somente um ponto em comum, que tangencia o eixo x.[/*][*][b]Terceira condição:[/b] Quando Δ < 0, a função não possui raiz real; logo, a parábola não intercepta o eixo x.[/*][/list]
A figura abaixo mostra as 3 condições para o caso em que a<0:
[b] [/b]O vértice da parábola y = 2x[sup]2 [/sup]- 4x + 5 é o ponto