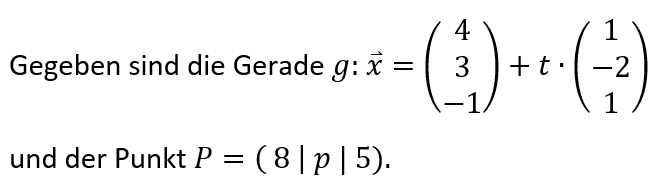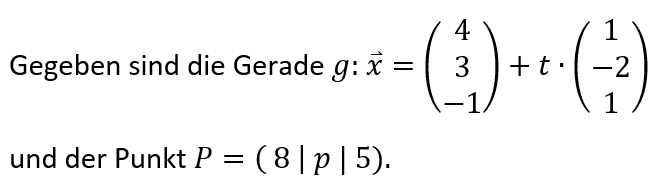Bestimmen Sie die fehlende Koordinate p des Punktes P so, dass der Abstand von P zu g 5 LE beträgt.[br][br][b]Hinweise zur Vorgehensweise:[/b][br]Machen Sie sich zunächst die Situation mithilfe der Abbildung 1 klar. Experimentieren Sie damit.[br]Versuchen Sie die möglichen Ergebnisse zu ermitteln.[br]Überlegen Sie sich eine Rechenstrategie, wie Sie die fehlende Koordinate rechnerisch bestimmen können.[br][br][b]Vielleicht können Ihnen auch die nachfolgenden Hinweise bei der Lösung der Aufgabe helfen (klicken Sie auf ANTWORTEN ÜBERPRÜFEN).[/b]
[list=1][*]Machen Sie sich mithilfe der dynamischen Abbildung klar, dass es genau zwei Ergebnisse gibt.[/*][*]Geben Sie die Koordinaten eines Punktes A an, der die Gerade g repräsentiert.[/*][*]Bestimmen Sie einen Vektor von P nach A, nennen Sie ihn d.[/*][*]Wenden Sie das Skalarprodukt an und ermitteln Sie einen Wert für t, für den Vektor d und der Richtungsvektor der Geraden g einen Winkel von 90° bilden [Ergebins: [math]t=\frac{8}{3}-\frac{1}{3}\cdot p[/math]][/*][*]Berechnen Sie mit dem Ergebnis aus 4 die Koordinaten von A und erläutern Sie die Bedeutung [Ergebnis: A=([math]\frac{20}{3}-\frac{1}{3}\cdot p,-\frac{7}{3}+\frac{2}{3}\cdot p,\frac{5}{3}-\frac{1}{3}\cdot p[/math]).[/*][*]Bestimmen Sie nun den Vektor von Punkt A nach Punkt P (dort darf jetzt nur noch die Unbekannte p enthalten sein.[/*][*]Wenden Sie die Formel zur Berechnung des Betrages (der Länge) eines Vektors an und bestimmen Sie mithilfe eines Rechners die Werte für p [Ergebnis: [math]p1=-15,3[/math], [math]p2=1,31[/math]][/*][/list]