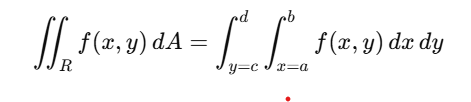
Introduction to Multiple Integration
[size=200][b][color=#ff7700]Multiple Integration[/color][/b][/size][br][br][justify]Through [b]multivariable calculus[/b] the concept of integration extends to functions having two or three variables with [b]double integrals[/b] and [b]triple integrals[/b] respectively. These integrals enable calculations to determine [i][color=#6d9eeb]areas[/color][/i] and [color=#6d9eeb][i]volumes[/i] [/color]and mass measurement as well as [i][color=#6d9eeb]center of mass[/color][/i] location and additional physical measurements for two-dimensional and three-dimensional regions.[br][br]A double integral serves as an extension of basic integration which applies to two-dimensional functions.[/justify][math]f\left(x,y\right)[/math]over a area [math]A[/math] or volume [math]V[/math] in space:
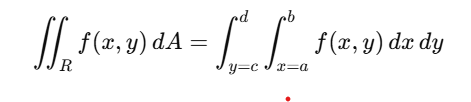
[justify]A triple integral serves as an extension of basic integration which applies to three-dimensional functions.[/justify][math]f\left(x,y,z\right)[/math] over a volume [math]V[/math] in space:
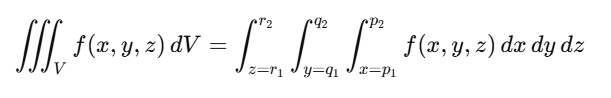
Triple Integral Formulas in Different Coordinate Systems
