•그래프가 아래로 볼록하다. ⇨[math]a>0[/math][br]•그래프가 위로 볼록하다. ⇨ [math]a<0[/math]
이차함수 y=ax^2+bx+c의 그래프와 a,b,c의 부호
이차함수 [math]y=ax^2+bx+c[/math]를 [math]y=a\left(x-p\right)^2+q[/math]의 꼴로 고치면[br][math]y=a\left(x+\frac{b}{2a}\right)^2-\frac{\left(b^2-4ac\right)}{4a}[/math][br]이므로 그래프의 축의 방정식, 꼭짓점의 좌표, [math]y[/math]축과의 교점의 좌표는 다음과 같다.[br]•축의 방정식: [math]x=-\frac{b}{2a}[/math][br]•꼭짓점의 좌표: [math]\left(-\frac{b}{2a},-\frac{\left(b^2-4ac\right)}{4a}\right)[/math][br]•y축과의 교점의 좌표: [math]\left(0,c\right)[/math]
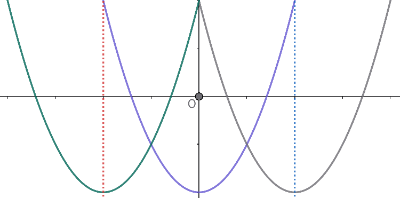
•축이 [math]y[/math]축의 왼쪽에 있으면 [math]-\frac{b}{2a}<0[/math]⇨[math]\frac{b}{a}>0[/math][br]즉, a와 b의 부호는 같다.[br]축이 [math]y[/math]축이면 [math]-\frac{b}{2a}=0[/math]이므로 [math]b=0[/math][br]•축이 [math]y[/math]축의 오른쪽에 있으면 [math]-\frac{b}{2a}>0[/math]⇨[math]\frac{b}{a}<0[/math][br]즉, a와 b의 부호가 다르다.[br]
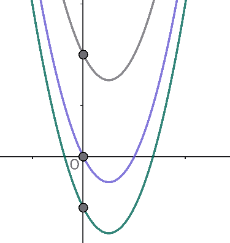
•[math]y[/math]축과의 교점이 [math]x[/math]축의 위쪽에 있다. ⇨ [math]c>0[/math][br]•[math]y[/math]축과의 교점이 원점이다. ⇨ [math]c=0[/math][br]•[math]y[/math]축과의 교점이 [math]x[/math]축의 아래쪽에 있다. ⇨ [math]c<0[/math]