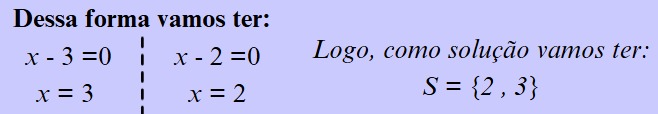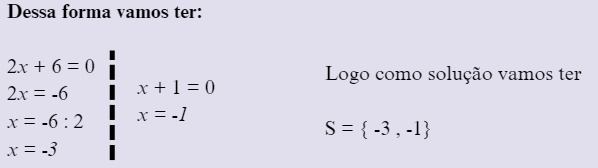Agora vamos aprender a como construir o plano que vamos utilizar na orientação da distribuição das peças, como será a distribuição das mesmas e ainda a forma correta de estar realizando a distribuição das peças.
Antes de começarmos, com as peças do material manipulativo concreto em mãos, pegue 3 placas, 9 barras e 6 quadradinhos e tente montar um retângulo qualquer com todas elas. Você conseguiu? Em princípio pode parecer muito difícil, mas daremos algumas dicas para facilitar esse trabalho. [br]
Desenhe um plano formado por duas linhas perpendiculares, conforme figura abaixo. Este plano te auxiliará na distribuição das peças para que não tentem montar os retângulos de forma aleatória.
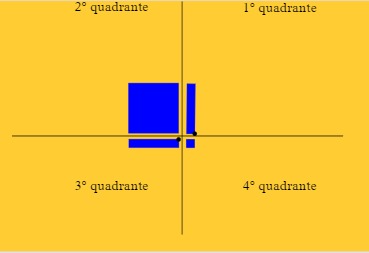
No plano construído você deve se atentar para a localização das peças. No primeiro e terceiro quadrantes ficam apenas as “barrinhas” que representam o “x”. No segundo quadrante ficam apenas as “placas” que representam o “ x² ”. No quarto quadrante ficam apenas os “quadradinhos” que representam os termos independentes.
abaixo estão apresentados um vídeo e imagens de como é a montagem correta e como é a montagem incorreta das peças no plano
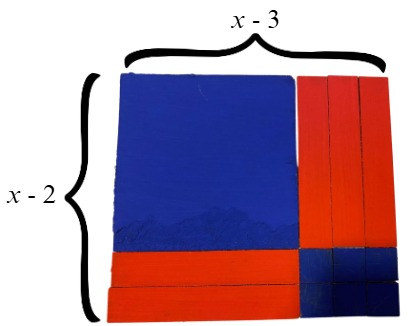
Agora, com o auxilio do professor vamos apresentar os procedimentos para montagem do primeiro retângulo de acordo com o tipo de equação do segundo grau que propomos. fazendo o detalhamento desses procedimentos: [br]Construa e represente x² - 5x + 6 num formato de retângulo.
Está será o último, após a montagem do retângulo o estudante poderá utilizar o recurso algébrico para determinar as raízes da equação. A decomposição da área do retângulo representa a forma fatorada da equação. Assim o estudante que igualar cada lado do retângulo a zero determinará as duas raízes da equação. Lembre-se que cada lado da placa tem a medida "x"
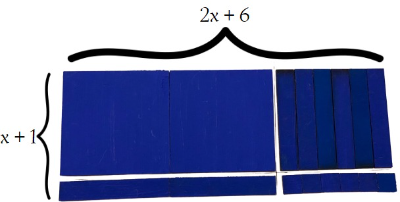
[br]Construa e represente 2x² + 8x + 6 num formato de retângulo.
Está será o último, após a montagem do retângulo o estudante poderá utilizar o recurso algébrico para determinar as raízes da equação. A decomposição da área do retângulo representa a forma fatorada da equação. Assim o estudante que igualar cada lado do retângulo a zero determinará as duas raízes da equação. Lembre-se que cada lado da placa tem a medida "x"