Revisão 4º período (Poliedros e Prismas)

Veja nos slides abaixo algumas definições e relações entre os elementos de um poliedro

Planificação do TETRAEDRO.

Questão 01

Qual o número de vértices, arestas e faces, respectivamente, desse tetraedro?

4, 6, 4 6, 4, 4 4, 4, 6 4, 4, 4

Questão 02

Cada face do tetraedro é um:

Triângulo retângulo Triângulo equilátero Triângulo obtusângulo Triângulo escaleno

Questão 03

Considerando que a área do triângulo utilizado nas faces do tetraedro é dada por [math]A=\frac{l^2\sqrt{3}}{4}[/math], qual é a área total desse tetraedro quando [math]l=4[/math]?

[math]8\sqrt{2}[/math] [math]16\sqrt{3}[/math] [math]4\sqrt{3}[/math] [math]6\sqrt{3}[/math]

Planificação do Hexaedro (Cubo)

Questão 04

Deslize o cursor da figura acima para o valor [math]a=3.5[/math] e observe os dados obtidos na representação 3D. Qual é o valor do volume desse cubo para este valor de aresta?

4,95 39,3 42,88 6,06

Observe as imagens abaixo para resolver à questão 05

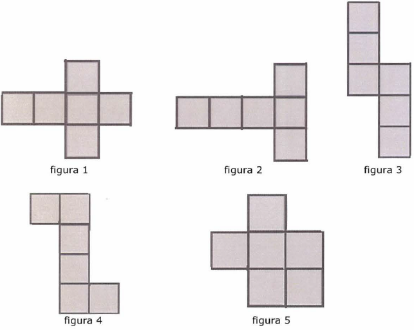
Questão 05

Das representações acima, a única que não corresponde a uma planificação do cubo é[br]

Figura 2 Figura 3 Figura 1 Figura 5 Figura 4

Planificação do Octaedro

Questão 06

O octaedro é considerado um poliedro regular porque:

Todas as suas faces são triângulos equiláteros congruentes e os ângulos entre as faces são iguais. É formado apenas por faces planas e possui 8 vértices. Suas faces são quadrados que se unem em torno de um vértice. Possui 8 faces, mas nem todas têm o mesmo formato. Todas as suas faces são triângulos escalenos congruentes e os ângulos entre as faces são obtusos.

Questão 07

Qual seria uma forma para determinar o volume do octaedro, dispondo apenas do tamanho da aresta "a"?

Aplicar a relação [math]V=a^3[/math], considerando que o octaedro apresenta proporções semelhantes às do cubo e, portanto, teria o mesmo volume para uma mesma medida de aresta. Somar as áreas das oito faces triangulares e dividir o resultado por 3, supondo que a área total do sólido possa ser usada diretamente para encontrar o volume sem necessidade de altura. Calcular o volume de um cubo de aresta "a" e multiplicar por 8, considerando que o octaedro possui 8 faces triangulares e, portanto, teria um volume equivalente à soma de oito sólidos menores com base triangular. Decompor o octaedro em pirâmides de base quadrada, utilizar a fórmula do volume da pirâmide e multiplicar por 2.

Questão 08

Quais são os nomes dos dois poliedros de Platão que não foram mencionados nas questões desta atividade?

Icosaedro e Pentaedro Dodecaedro e Decaedro. Dodecaedro e Icosaedro. Icosaedro e Decaedro

Relembre a relação de Euler e a relação entre o número de arestas e o formato das faces

Questão 09

Um poliedro convexo tem 30 arestas e 12 faces pentagonais. Quantos [b]vértices[/b] possui esse poliedro?

60 36 32 20

Questão 10

Um poliedro convexo é formado por 5 faces pentagonais e 5 faces triangulares. Qual é o número total de arestas desse poliedro?

35 25 20 10

Questão 11

Um poliedro convexo tem 32 faces, sendo 20 hexágonos e 12 pentágonos. O número de vértices deste poliedro é:

72 90 56 60

[size=200][i]Prismas[/i][/size]

Os prismas são sólidos geométricos (poliedros) com duas bases poligonais congruentes e paralelas, conectadas por faces laterais que são paralelogramos (retângulos ou não).

Observe na imagem abaixo os elmentos de um prisma

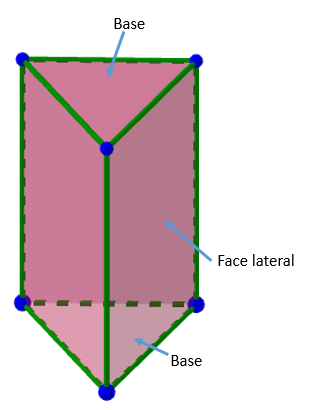
Manipule a figura abaixo para visualizar estes elementos em 3 dimensões

Questão 12

Os prismas acima de acordo com a base recebem o nome de, respectivamente:

Pentagonal, hexagonal e quadrangular Quadrangular, pentagonal e hexagonal Quadrangular, hexagonal e pentagonal Pentagonal, quadrangular, e hexagonal

Questão 13

Quantas bases possui cada prisma?

4 2 3 5

Questão 14

As bases dos prismas, em geral, são formadas por:

Sempre dois quadrados congruentes e paralelos Sempre dois pentágonos congruentes e paralelos Quaisquer polígonos congruentes e paralelos Quaisquer polígonos congruentes e perpendiculares

Questão 15

As faces laterais dos prismas são sempre:

Pentágonos (regulares ou não) Quadrados (congruentes ou não) Triângulos (equiláteros ou não) Paralelogramos (retângulos ou não)

Relembre como calcular a área total e o volume de um prisma

Reveja as fórmulas de área de alguns polígonos:

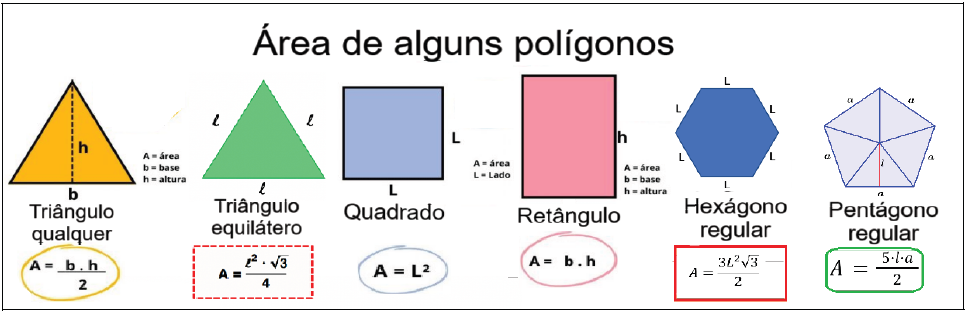
Questão 16

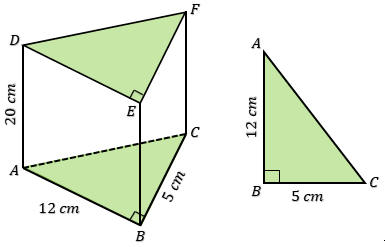
Considere este prisma triangular irregular cuja base é um triângulo retângulo. Calcule: [br][size=100][size=85](Para cada item, escreva somente o número correspondente ao resultado)[/size][/size]

a) O comprimento do lado [math]\overline{AC}[/math].[br][size=85](Sugestão: utilize o teorema de Pitágoras: [math]a^2+b^2=c^2[/math])[/size]

b) A área da base do prisma ([math]A_b[/math].)

c) A área lateral desse prisma ([math]A_l[/math])

d) A área total do prisma