Math 8 Tasks
Distance learning activities for 8th Grade Mathematics.
Table of Contents
- Pythagorean Theorem
- Distance Between Two Points
- Areas of Squares and Right Triangles
- Lengths of Squares and Right Triangles
- Discover Pythagorean Theorem
- Missing Side Lengths
- Trouble with Triangles
- More Trouble with Triangles
- Angle Relationships
- Transformations
Distance Between Two Points
Learning Goal
Students will explore distance between two points in a coordinate plane and learn how this relates to right triangles.
Visual 1: Click, drag, and drop the points to explore the distance between them.
Question 1: Use the visual to...
Find the distance between each set of two points:[br][list=1][*](0,0) and (5,0)[/*][*](0,0) and (0,5)[/*][*](7,3) and (5,3)[/*][*](-6,-4) and (-6,4)[/*][/list]Explain how you know.
Question 1: Check your answer.
Visual 2: Click, drag, and drop the points to explore the distance between them.
Question 2: Use the visual to...
Find the distance between (1,1) and (8,6).[br][list=1][*]What is different this time?[/*][*]Can this exact distance be found? Why or why not?[/*][/list]
Question 2: Check your answer.
Attention: Did you notice the right triangle?
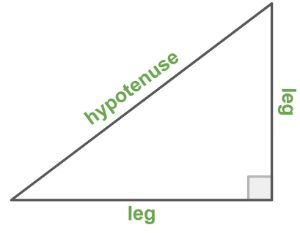
Wherever there is a diagonal distance, there is also a right triangle.
[list][*]The [b][color=#6aa84f]longest side[/color][/b] of the right triangle (called the [b][color=#6aa84f]hypotenuse[/color][/b]) is the diagonal distance.[/*][*]The two [color=#6aa84f][b]shorter sides[/b][/color] of the right triangle (called the [color=#6aa84f][b]legs[/b][/color]) make up the horizontal and vertical components of the diagonal distance.[/*][/list]Click the most correct choice.
Visual 3: Click, drag, and drop the points and the lengths to estimate the distance.
Question 3: Use the visual to...
Estimate the distance between each set of two points in terms of the lengths of the [color=#6aa84f][b]hypotenuse[/b][/color] and [color=#6aa84f][b]legs[/b][/color] of the right triangle:[list=1][*](0,0) and (6,3)[/*][*](-3,5) and (2,1)[/*][*](-7,-4) and (3,-8)[/*][*](4,-2) and (0,2)[/*][/list]What patterns are there between these lengths? Use the words [b][color=#6aa84f]hypotenuse[/color][/b] and [color=#6aa84f][b]leg[/b][/color].