Gegeven zijn twee rechten a en b in [math]\mathbb{R}^3[/math][br][math]a\leftrightarrow\frac{x-1}{2}=\frac{y}{3}=\frac{z-3}{-4}[/math] en [math]b\leftrightarrow\begin{cases}3x-2y=-21\\4y+3z=31\end{cases}[/math][br]Bepaal de onderlinge stand van de rechten a en b

De uitdrukking [math]\ln(x^2+2x+1)-\ln(x+1)[/math] kan men vereenvoudigen tot

Welke uitspraak over de asymptoten van de grafiek van [math]f(x)=\frac{\sqrt{9x^6-x}}{x^3+1}[/math] is correct

Bereken [math]\lim\limits_{x\to+\infty}\sqrt{x^2+ax}-\sqrt{x^2+bx}[/math]

De functie f is continu voor x=0 en is gedefinieerd voor -1<x<1 door[br][math]f(x)=\begin{cases}\frac{2a}{x}\ln(1+x)&&als&-1<x<0\\[br]b&&als&x=0\\[br]\frac{x^2\cos x}{1-\sqrt{1-x^2}}&&als&0<x<1\end{cases}[/math][br]Bepaal de waarden van a en b

Gegeven is de functie [math]f:\mathbb{R}_{0}^{+}\to\mathbb{R}[/math] met voorschrift [math]f(x)=x\ln(x)[/math]. Bereken [math]\frac{f'(e)}{f'(1)}[/math]

Gegeven is de functie met als voorschrift [math]f(x)=e^{px}[/math]. De raaklijn aan de grafiek in het punt met x-coördinaat gelijk aan 1 gaat door de oorsprong als

Bereken [math]\lim\limits_{x\to+\infty}\sqrt{x}\left(\sqrt{x-5}-\sqrt{x}\right)[/math]

Bereken [math]f^{(4)}\left(\frac{\pi}{4}\right)[/math] waarbij met (4) de vierde afgeleide wordt bedoeld en [math]f(x)=\sin(x)\cos(x)[/math]

De vergelijking van de raaklijn aan de grafiek van [math]f(x)=2+(x-1)e^x+\frac{3}{2}\ln\left(x^2\right)[/math] in P(1,f(1)) is

Beschouw in [math]\mathbb{R}^3[/math] de rechte l met vergelijking [math]\frac{x-1}{5}=\frac{2-y}{-3}=\frac{z}{4}[/math]. Welk van de volgende uitspraken is waar?

Bepaal het absoluut max van de grafiek van de functie [math]f(x)=\frac{\ln x}{\sqrt{x}}[/math] over het interval [math][1,e^4][/math]

Beschouw de reële functie f met voorschrift [math]f(x)=(x^2-9)e^{-x}[/math]. Welke bewering over het functieverloop is dan als enige correct?

Bepaal het domein van [math]f(x)=\ln(1-2x+\sqrt{x})[/math]

Van welke DV is [math]y=\frac{\ln(x)}{x}[/math] een oplossing?

Bepaal het domein van [math]f(x)=\sqrt{3-\log_{2}(x+5)}[/math]

De afbeelding is een parellogram. Zij M het midden van [PS] en N het midden van [PQ]. De vector [math]2\overrightarrow{MN}[/math] kan geschreven als volgende lineaire combinatie:

De uitdrukking [math]R=\frac{a^2b}{c}[/math] met a, b en c strikt positieve getallen kan herschreven worden tot

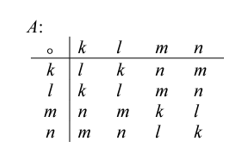
[math]A,\circ[/math] is een commutatieve groep omdat

Hoeveel oplossingen heeft volgende vergelijking in [math]x\in[0,\pi][/math]:[math](\sin x-2024\cos x)\cdot \ln\left(x^2-6x+\frac{19}{2}\right)=0[/math]

Gegeven in de driedimensionale ruimte is het vlak [math]\alpha\leftrightarrow x+2y+3z=29[/math] en het punt [math]P(5,-2,0)[/math]. Als we dit punt P spiegelen t.o.v. het vlak dan is de x-coördinaat van het gespiegelde punt:

[math]\lim\limits_{x\to 0}\frac{e^x}{\ln\left(x^2\right)}=[/math]

Bepaal de rico van de raaklijn aan de grafiek van [math]f(x)=\ln\left(\frac{e^{2x}\cdot\sqrt{x+3}}{x^2+1}\right)[/math] in het punt P met x-coördinaat 1

De grafiek van de functie [math]f(x)=\frac{3-2e^{2x}}{4e^{2x}+2[/math] heeft 2 HA y=A en y=B. Bepaal A+B

Welk vlak staat loodrecht op het vlak [math]\alpha\leftrightarrow 3x+2y+z=0[/math]

[math]\ln\left(2e^x+1+e^{2x}\right)=[/math]