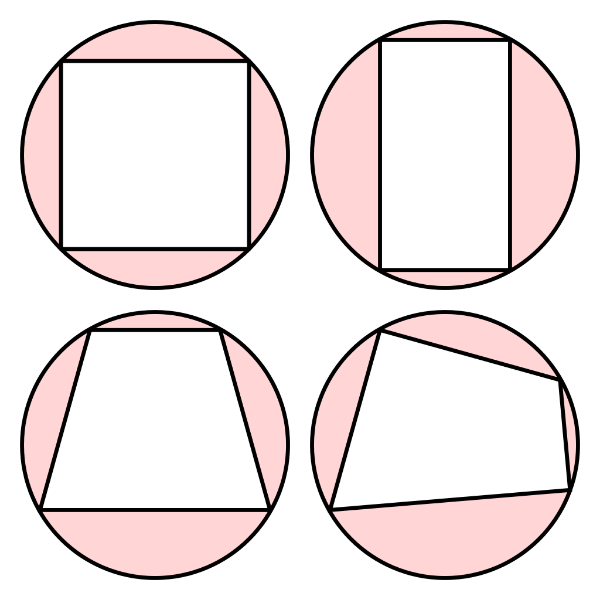
fuente: https://en.wikipedia.org/wiki/Cyclic_quadrilateral
Un polígono está inscrito en un círculo si sus vértices se encuentran en el círculo. A los cuadriláteros que están inscritos se les llama [b]cuadriláteros cíclicos[/b]. [br][br]En la figura previa, podemos ver ejemplos de cuadriláteros cíclicos.
Si tenemos un cuadrilátero cíclico, entonces los ángulos que inscriben los mismos arcos serán congruentes.[br][br]Veamos la siguiente figura para mostrar un ejemplo.
Un cuadrilátero es cíclico si y solo si sus ángulos opuestos son suplementarios.[br][br][b]Demostración[/b]: Supongamos que tenemos un cuadrilátero cíclico ABCD
Entonces por la relación entre ángulos inscritos y centrales que abren el mismo arco, se tiene que [math]\angle CDA=\frac{1}{2}\angle COA[/math] y [math]\angle ABC=\frac{1}{2}\angle AOC[/math]. Sumando estas ecuaciones se obtiene:[br][br][math]\angle CDA+\angle ABC=\frac{1}{2}\angle COA+\frac{1}{2}\angle AOC=\frac{1}{2}\left(\angle COA+\angle AOC\right)[/math][br][br]Pero [math]\angle COA+\angle AOC=360^\circ[/math]. Por lo tanto, [math]\angle CDA+\angle ABC=180^\circ[/math]. [br][br]Recíprocamente, supongamos que el cuadrilátero ABCD cumple que [math]\angle CDA+\angle ABC=180^\circ[/math]. Trazamos el círculo que pasa por los puntos A, B, y C. Sea D' el punto de corte del lado AD con el círculo.
Como el cuadrilátero ABCD' es cíclico, por lo que acabamos de demostrar se cumple que [math]\angle CD'A+\angle ABC=180^\circ[/math]. Por lo tanto, [math]\angle CD'A=\angle CDA[/math]. Pero esto implica que DD'=0. Luego D=D' y el cuadrilátero ABCD es cíclico.
Si ABCD es un cuadrilátero, tal que sus diagonales se intersecan en P, entonces ABCD es cíclico si y solo si [math]PA\cdot PC=PB\cdot PD[/math].[br][br][b]Demostración[/b]: Como [math]\frac{PA}{PB}=\frac{PD}{PC}[/math] y [math]\angle APB=\angle CPD[/math], entonces el ΔPAB es semejante al ΔPDC por LAL. Entonces [math]\angle PBA=\angle DCP[/math] y esto implica que [i]el cuadrilátero ABCD es cíclico[/i].

