The girih method working with a fixed set of polygons creates stars with a fixed number of points. I addition to this system a second method was established. In circle bundles of radii were drawn. Intersection points of these radii define segments, forming polygons. This construction method allows combining stars with a different number of points within one pattern. In the article [url=https://www.nexusjournal.com/volume-18/volume-18-number-1-2016.html]Girih for Domes: Analysis of Three Iranian Domes[/url] the authors Mohammad Hossein Kasraei, Yahya Nourian and Mohamadjavad Mahdavinejad describe this method as the radial girih method or [b][i]Dast-Gardan girih[/i][/b].[br][br][br]

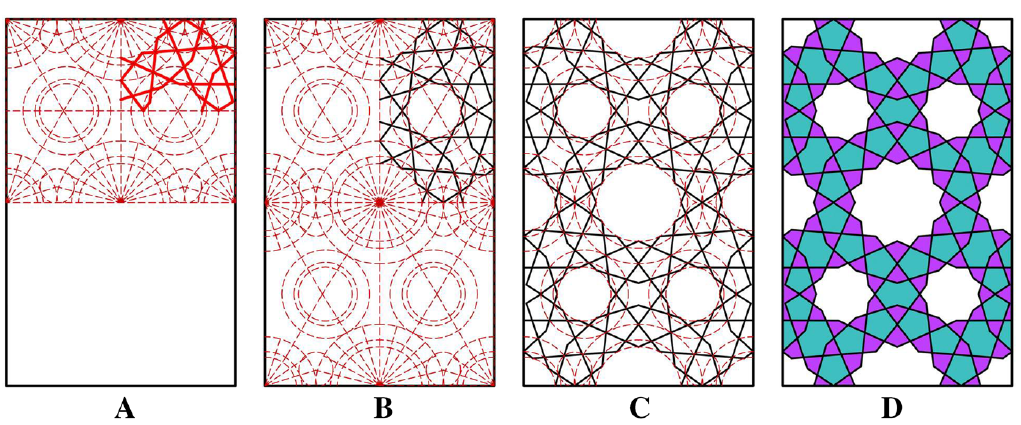
In the example you can see how the pattern  is constructed. [list][*]Within a unit repeat concentric circles are drawn on every corner point.[/*][*]These circles are divided into congruent sectors.[/*][*]Diagonals in the unit repeat define the center points of additional circles [b][i](step A)[/i][/b].[/*][*]Connecting intersection points of radii and circles generates a line pattern [b][i](step B)[/i][/b].[/*][*]This pattern is mirrored on the axes of symmetry if the unit repeat [b][i](step C)[/i][/b].[/*][/list]The result [b][i](step D)[/i][/b] is a geometric pattern that combines 12-pointed stars with 9-pointed stars.

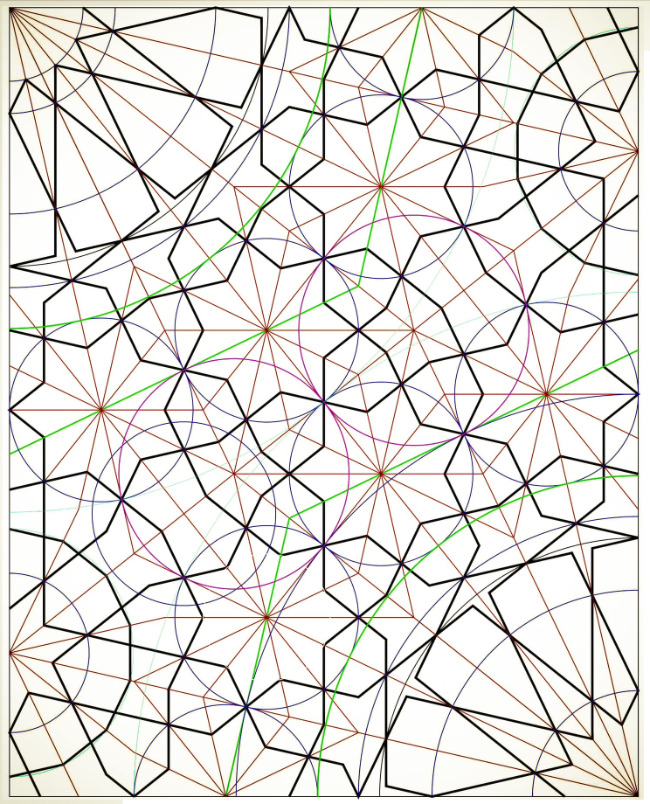
A nice example is shown in a drawing by Aslam Qureshi.[br]The construction starts with two quart circles in opposed corners of a rectangle and smaller, tangent circles. With bundles of radii and intersections points a balanced 7-fold pattern is created.