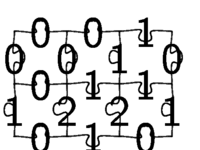
Puzzle Binaire Ternaire
Les six pièces du puzzle
Ces six pièces de puzzle permettent de passer d'une écriture binaire d'un nombre (à l'horizontal) en son écriture ternaire (en vertical) et vice-versa. Il faut les imprimer et les découper, en assez grand nombre. Si vous n'avez pas de découpeuse laser, coupez les pièces selon les carrés.[br][br]Composez d'abord l'écriture binaire (resp. ternaire) d'un nombre horizontalement (resp. verticalement), complétez par des 0 à gauche (resp. en haut) en posant des tuiles, puis résolvez le puzzle vers le haut et à droite (resp. vers la gauche et en bas) pour arriver à une verticale (resp. horizontale) donnant son écriture en base trois (resp. deux). [br][br]Les chiffres qui apparaissent sur les arêtes ont une signification à tous les endroits, permettant de coder votre nombre en [url=https://www.geogebra.org/m/azvfvm9f]multibase[/url].[br][br]Vous pouvez vous poser d'autres questions: étant donné un fragment de puzzle, comment peut-on le continuer, jusqu'où, dans quelle(s) conversion(s) entre binaire et ternaire intervient-il?[br][br]Si vous prenez par exemple ces six pièces comme départ, vous voyez que vous êtes obligé·e, afin de commencer par des 0 en haut et à gauche, d'obtenir à la fin 1010₂=101₃=8+2=9+1, soit dix.[br][br]Vous pouvez, à partir de ces pièces, paver le plan entier, ne serait-ce qu'avec des 0. Y-a-t-il d'autres pavages du plan à partir de ces tuiles? On s'intéresse au quart de plan NO, est-ce que les autres quarts de plan ont une signification arithmétique?
