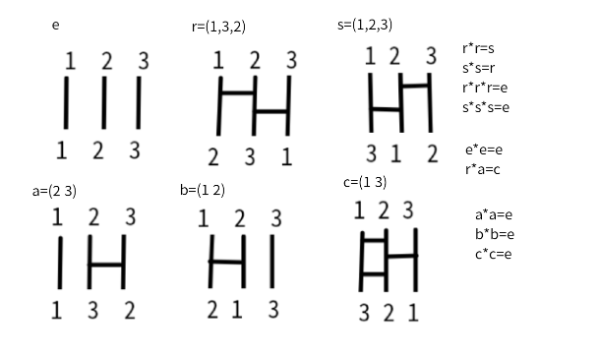
群の入れ子
1.群の中にも群がある?
[b][size=150][b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[/b][br][br][/size][/b]3本あみだくじは1,2,3の3個の要素の番号の入れ替え(置換)です。[br]あみだくじの集合は、置換の集まりで連結という2項演算について群の性質をもっています。[br]このようなn個すべての置換の集合の群を[b][color=#0000ff]対称群Symmetry[/color][/b]といい、[br]Snとかき、要素はn!個です。[br][b][size=150][br]<群になる部分をさぐってみよう>[/size][/b][br]3本あみだくじ群はS3で、要素は6個です。[br][b]部分集合[/b]は[b]要素[/b]とはちがいますから、部分集合は6個ではないです。[br]S[sub]3[/sub]={e, r, s , a, b, c}[br]#S[sub]3[/sub]=6, |S[sub]3[/sub]|=6, n(S[sub]3[/sub])=6。[br][b]部分集合は要素を集めて作った集合[/b]です。[br]6個の要素を入れる入れないの問に対してY/Nの回答をすると[br]2×2×2×2×2×2=2[sup]6[/sup]=64通りの回答ができるでしょう。[br]だから、全部Yにした全体と同じ集合と全部Nにした空の集合も入ってます。[br]視点を変えると部分集合の要素数ごとにカウントすると、組み合わせの数で求められますね。[br]6C0=1[br]6C1=6[br]6C2=15[br]6C3=20[br]6C4=15[br]6C5=6[br]6C0=1[br]よく考えてみると、部分集合が64個あるからといって、[br]それらが群になれる保証はない。[br]というか、ほとんど群にはなれないでしょう。[br]S[sub]3[/sub]={e, r, s , a, b, c}[br]でeが入るものに限定して探そう。[br]eがないものは不要だから、[br]64/2=32個の部分集合が候補になる。[br]また、[u][b]全体集合{e, r, s , a, b, c}[/b][/u][br]が群なのは当たり前だし、[br][b][u]恒等置換だけの集合{e}[/u][/b]でもeの逆元がeだから、e単独でも、群と言える。[br]こういうつまらない当たり前の部分集合は取り除く。[br]すると、32-2=30個が候補になる。[br][br][b][size=150]<試行錯誤で群になる部分集合、つまり、部分群をさぐろう>[br][/size][/b]では、範囲をせばめながら群を手探りでさがしてみよう。[br]でも、30個といっても多すぎる。[br]たとえば、巡回置換のs=(1 2 3)があれば、s[sup]3[/sup]=eだから、s[sup]2[/sup]=s[sup]-1[/sup]=rとなり、sとrをバラバラにできない。[br]そう考えると、r, s があるものつまり、[color=#0000ff][b]e,r,sの3個[/b][/color]以上もつか[b][color=#0000ff]eだけでr,sは持たない[/color][/b]かのどちらかになる。[br]つまり、e,r,sの3要素に関しては[br][u][b]{e}か{e, r, s}[/b][/u]かの2択になるということだね。[br]これに{a,b,c}をまぜなくても群ができることは明らかだね。[br]当たり前でない群は、今のところ{e,r,s}だけだ。[br][br]・次は{e}と{a,b,c}をからめるものを考えよう。[br]もちろん[color=#0000ff][b]a*a=e, b*b=e, c*c=e[/b][/color]だから、自分自身が逆元になれる。[br][b][u]{e, a},{e, b},{e, c}[/u][/b]という3つの部分群ができるね。[br]a*b=(2 3)(1 2)=(1 3 2)[br]b*a=(1 2)(2 3)=(1 2 3)[br]a*c=(2 3)(1 3)=(1 2 3)[br]c*a=(1 3)(2 3)=(1 3 2)[br]b*c=(1 2)(1 3)=(1 3 2)[br]c*b=(1 3)(1 2)=(1 2 3)[br]だから、[color=#0000ff][b]a,b,cの2つが入ってしまうと、r,sのどちらかになる[/b][/color]ため、r,sをセットにして入れることになる。[br]なので、{e}と{a,b,c}をからめると、a,b,cのどれか1つだけを入れる以外にない。[br][br]・最後に、[u]{e, r, s}に対して、{a, b, c}にからめる場合を考える。[br][/u][color=#0000ff][b]2つの互換b=(1 2)と巡回置換s=(1 2 3)の積で全体の6要素を表せることは、前回の演習で確認した。[br][/b][/color]s[sup]3[/sup]=e, b[sup]2[/sup]=eだから、eができる。[br]言い換えると、s[sup]-1[/sup]=s[sup]2[/sup], b[sup]-1[/sup]=b[br]s[sup]-1[/sup]=(1 3 2)[br]b s[sup]-1[/sup]=(1 2)(1 3 2)=(1 3)[br]s b s[sup]-1[/sup]=(1 2 3)(1 3)=(2 3)[br]これで、3つの互換と2つ巡回置換と恒等置換eが表現できた。[br]ぜんぶで6個の置換を表すことがでできた。[br]ということは、[br]{e,r,s}に{b}をまぜただけで、全体と同じになる。[br]だから、これ以上自明でない部分群はできないことになるね。[br][br][size=150][size=200]<3次の対称群S[sub]3[/sub]の部分群のまとめ>[br][/size]もともと、対称群は置換群ですから、その部分群は置換の群、置換群です。[br][/size][size=200][size=150][b]・[/b]自明な部分群[/size][b][br]全体群{e,r,s,a,b,c}[br]恒等群{e}[br][/b][size=150][b]・[/b]自明でない部分群[br][/size][b]巡回群でもある置換群{e, a}, {e, b},{e, c},{e, r, s}[br][/b][/size]

2.群のタイプ
[b][size=150]<巡回群>[br][/size][/b]たとえば、[br][b]巡回群{e,a}の場合[/b]、aが元になり、a, a[sup]2[/sup],a[sup]3[/sup],a[sup]4[/sup],a[sup]5[/sup],....とa倍を繰り返すと、群の全要素a,eを生成できる。[br][b]巡回群{e,r,s}の場合[/b]、sが元になり、s, s[sup]2[/sup],s[sup]3[/sup],s[sup]4[/sup],s[sup]5[/sup],....とs倍を繰り返すと、群の全要素s,r,eを生成できる。[br]群の要素数が2、3だと、巡回群しかないかもしれません。[br]そもそも3次の置換群は集合としては3要素の番号の順列としての6要素をもっていました。[br]だから、群の要素数は6です。[br]群の要素数が増えると、さまざまなパターンの群が登場するようです。[br]さきの巡回群の要素数は2と3で素数でした。[br]これが3次の置換群の要素数6のように、合成数になると、[br]さまざまな関係性が生まれそうです。[br]群の中に群が入っているということは、群と群の関係を[br]試行錯誤ではなく、もっと互いの構造や機能のつながりからさぐる必要がありそうだね。
++記号の演習
[size=150][b]<数学の抽象化は概念化と切り離せない>[br][/b][/size][br]数学の抽象化は概念化、[br]つまり「用語と記号」の「約束」の世界だ。[br]群の「約束記号と用語」になれるために、[color=#0000ff][b]群の性質[/b][/color]を記号・用語で確認する演習をしたい人はどうぞ。[br][br][b][size=150]<部分群の条件>[br][/size]HがGの部分群になる条件[/b]は任意のx,y∈Hに対して[b]xy[sup]-1[/sup]∈H[/b]であることです。[br]⇒自明。逆は、単位元e=xx[sup]-1[/sup]∈H,逆元Y=y[sup]-1[/sup]=ey[sup]-1[/sup]∈H,閉性xy=xy=x(y[sup]-1[/sup])[sup]-1[/sup]=xY[sup]-1[/sup]∈H[br]HがGの部分群なら[b][math]H\le G[/math][/b]とかく。[br][br][b][size=150]<群表>[br][/size][/b]群の要素どうしの演算結果を九九表のように行列表にしたもの[br]群表から群の特徴をさぐろう[br][b](位数1の群)[br]単位元eだけ[/b]の集合にe*e=eという演算が定義されている。[br]表を作るまでもない。[br][b](位数2の群)[br][/b]G={e,a}[br] e*e=e, e*a=aは確定。[br]a*a=aかa*a=eのどっちかな?[br]a*a=aなら、aは単位元になってしまうから。a*a=eとなる。だから、Gは位数2の[b]巡回群[/b]しかないね。[br][b](位数3の群)[br][/b]G={e,a,b}[br] e*e=e, e*a=a,e*b=bは確定。[br]a*a=eか、a*a=bのどっちかな?[br]a*(e,a,b)=a,e,bとなり、aが単位元になるからだめ。a*(e,a,b)=a,b,e。[br]だから,aが生成元とすると、b=a*a, bが生成元とするとa=b*bとなり、Gは位数3の[b]巡回群[/b]しかないね。[br][b](位数4の群)[br][/b]G={e,a,b,c}[br]e*e=e,e*a=a,e*b=b,e*c=cは確定。[br]逆元がa*a=b*b=c*c=eと自己逆元にするか、a*a=b,b*b=e,c*c=bとするかで別のしくみになる。[br]どの元も自己逆元だから位数が2となり、巡回群にはならないね。これが何者かは後で考えよう。[br]自己逆元にならないaを使うと、a*a=bだから、a[sup]4[/sup]=b*b=eで、aが生成元になる巡回群になるね。[br]この例だけではわかりませんが、[br][b]位数が素数だと巡回群になりそう。[br]位数が合成数[/b]だと、群の位数だけかけなくても単位元になるときの自由度が増えるので、[br]巡回群以外の群が生まれそうだね。[br][br][color=#9900ff][u][b][size=150]質問:巡回群の群表を作るにはどうしたらよいでしょうか。[br][/size][/b][/u][/color][br]基本になる関数をそのまま使います。[br]巡回群の要素を辞書で作りまますが、辞書リストをSとし、[br]辞書の名前をSN=["g0","g1",....,"g5"]となします。[br]辞書と名前をセットにする関数[b]Ndic[/b]を新しく作り、その戻り値をNlistにしておけば、[br]maketableを実行するだけで作れるね。[br]#[IN]Python[br]#=========================================================[br]def ami2dic(ami):[br] return dict(zip(ami , ami[1:] + [ami[0]]))[br]def amis2dics(amis):[br] return [dict(zip(ami , ami[1:] + [ami[0]])) for ami in amis][br]# kの辞書dic_aによる行先を返す。辞書にないなら行先はk。[br]def ami_go(k,dic_a):[br] return dic_a[k] if k in dic_a.keys() else k[br]#あみだの辞書a,bの連結をする。[br]def conL(a,b):#a,bの順に演算する。[br] keys = list(set(list(a.keys()) + list(b.keys())))[br] dic ={key:ami_go(ami_go(key,a),b) for key in keys if key !=ami_go(ami_go(key,a),b)}[br] if len(dic)==0:[br] dic={1:1}[br] return dic[br]def conR(a,b):#b,aの順に演算する。[br] return conL(b,a)[br]#アミダを、(辞書,名)のタプルのリストにする。[br]def rotdic(S,SN):[br] dic=[ami2dic(x) for x in S][br] return list(zip(dic,SN))[br]# あみだ辞書dic_aを名で返す。[br]def name(dic_a):[br] global Nlist[br] return [item[1] for item in Nlist if item[0]==dic_a][0][br]# あみだ辞書集dicsを名のリストで返す。[br]def names(dics):[br] global Nlist[br] return [item[1] for item in Nlist for b in dics if item[0]==b][br]# あみだ辞書の集合Hと辞書aを演算した結果リストを返す。[br]def Ha(H,a):[br] global Nlist[br] res=[][br] for b in H:[br] res +=[item[1] for item in Nlist if item[0]==conR(b,a)][br] return res[br]def aH(a,H):[br] global Nlist[br] res=[][br] for b in H:[br] res +=[item[1] for item in Nlist if item[0]==conR(a,b)][br] return res[br]#==================================以上が基本関数====================[br]#辞書リストS,名リストSNから(辞書、名)のタプルのリストにする。[br][b]def Ndic(S,SN):[br] return list(zip(S,SN))[br][/b]def pow(G,n):[br] return polymultiR([ G for x in range(1,n+1)]) if n>0 else {1:1}[br]#群表を作る[br]def maketable():[br] global Nlist[br] G = [x[0] for x in Nlist][br] print("* ",names(G))[br] for item in G:[br] print(name(item),aH(item,G))[br] return True[br]#=================================以上が今回の前準備==================[br][b]g=[1,2,3,4,5,6][br]S=[pow(ami2dic(g),index) for index in range(6)][br]SN=["g" + str(x) for x in range(6)][br]Nlist=Ndic(S,SN)[br]maketable()[br][/b]#==================================================================[br][OUT][br] * ['g0', 'g1', 'g2', 'g3', 'g4', 'g5'][br]g0 ['g0', 'g1', 'g2', 'g3', 'g4', 'g5'][br]g1 ['g1', 'g2', 'g3', 'g4', 'g5', 'g0'][br]g2 ['g2', 'g3', 'g4', 'g5', 'g0', 'g1'][br]g3 ['g3', 'g4', 'g5', 'g0', 'g1', 'g2'][br]g4 ['g4', 'g5', 'g0', 'g1', 'g2', 'g3'][br]g5 ['g5', 'g0', 'g1', 'g2', 'g3', 'g4']