Equacions, inequacions i sistemes
Table of Contents
- Factorització de polinomis
- Polinomis: factorització_CCSS
- Solucions gràfiques d'equacions
- Resolució gràfica d'equacions
- Solució gràfica d'un sistema d'equacions
- Resolució de sistemes d'equacions
- Resolució per a 3 incògnites
Polinomis: factorització_CCSS
Representació de polinomis
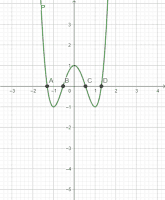
Un [b]polinomi[/b] és la suma/resta d'un o més monomis; entent els monomis com l'expressió algebraica formada pel producte d'un nombre per una o més lletres. [br]Per exemple: [i]P(X)=2x[sup]4[/sup]-4x[sup]2[/sup]+1[/i][br][br]La imatge següent mostra la[b] representació gràfica[/b] del polinomi exemple:
Arrels d'un polinomi
Coneixem com [b]arrels d'un polinomi[/b] els coeficients pels quals el valor numèric del polinomi és igual a 0; és a dir, els valors que s'obtenen d'igualar a 0 el polinomi i resoldre'n l'equació que es determina. [br][center][i]P(a)=0, essent a una arrel del polinomi[br][/i][/center]Pel procés de factorització d'un polinomi es troben les arrels d'aquest[br][br]Gràficament aquestes arrels del polinomi són els punts d'interseció amb l'eix x, és a dir quan y=0. Fixant-nos amb la imatge anterior es pot veure que els punts d'intersecció són A, B, C, D; 4 punts atès que és un polinomi de grau 4. A continuació pots escriure el polinomi que creguis, veure'n la seva representació gràfica, la factorització i punts d'interesecció.
[u]Activitat:[br][/u]a) Pensa i escriu en un full 2 polinomis de grau 4 i 2 de grau 3.[br]b) Fes-ne la descomposició factorial i busca les seves arrels[br]c) Comprova les solucions fent ús de l'[i]applet [/i]anterior[br]d) Reflexiona com poden serien les solucions de qualsevol tipus d'equacions.
Resolució gràfica d'equacions
Les [b]equacions[/b] són igualtats que es compleixen per un valor de la [u]incògnita[/u], generalment expressada per la lletra [i]x[/i].[br]Quan es[b] resolen equacions[/b] el que estem fent és buscar el valor pel qual es compleix la igualtat. El procediment per resoldre les equacions es centra en igualar a 0 l'equació de manera que es troben les solucions, també conegudes com arrels.[br][br]Tenint en compte el que s'ha comentat a l'apartat de factorització de polinomis el que estem fent és buscar els punts d'interesecció de la gràfica que representen les funcions amb l'eix X (x=0). [br]A continuació pots veure l'exemple d'algunes equacions:
[u]Activitat:[br][/u]Comprova els resultats de les equacions que es plantegen. [br]Prova a l'applet següent altres equacions. Cal introduir-les ja igualades a 0 i amb l'opció [icon]/images/ggb/toolbar/mode_roots.png[/icon] arrels comprova els resultats.
Resolució de sistemes d'equacions
Un [b]sistema d'equacions[/b] és un conjunt d'equacions. El que es preten en la seva resolució és trobar la/les solució/ns comuna/es per a totes les incògnites tenint en compte que s'han de complir per a totes les equacions del sistema. Hi ha [u]sistemes d'equacions lineals[/u] quan el grau de les equacions és 1, mentre que si el grau és més gran es consideren [u]sistemes d'equacions no lineals.[br][br][/u]Per resoldre els sistemes d'equacions es poden utilitzar mètodes analítics, per exemple el mètode per reducció, igualació, substitució..., però també podem utilitzar mètodes gràfics. En aquest cas la solució del sistema és on les equacions intersequen entre elles.
[u]Activitat:[br][/u]a) Resol els sistemes d'equacions proposats a l'aula pel mètode que et sigui millor[br]c) Comprova en aquesta aplet les solucions trobades