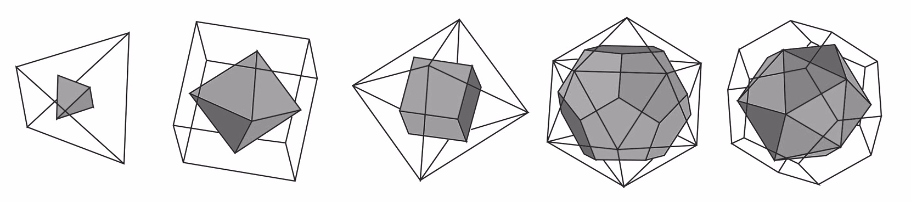
icosahedron and dodecahedron
The icosahedron and the dodecahedron are two of the 5 Platonic solids.[br]These solids form pairs and the icosahedron and the dodecahedron are one of them.[br]The remarkable thing about them is that you can keep on placing the solids into one another.[br]The midpoints of the 20 side surfaces of the icosahedron can be connected to form a dodecahedron and at their turn the midpoints of the 12 side surfaces of a dodecahedron form an icosahedron.

So you might as well say that you can connect the midpoints of the 12 pentagonal side surfaces to form 3 golden rectangles.[br]And talking about pentagons [math]\varphi[/math] is not at all a stranger. [br]So you can find [math]\varphi[/math] in polygons were angles (or mulples) of [math]\frac{\pi}{10}[/math] occur as well in solids.