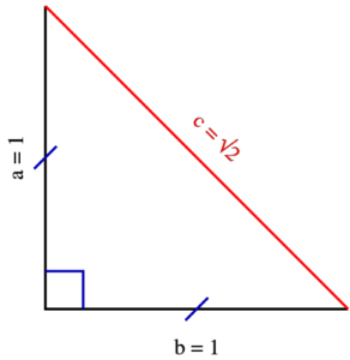
[size=200][b][i]La Storia dei Numeri Irrazionali[/i][/b][/size][br][br][br][color=#222222]Come detto in precedenza, i Pitagorici pensavano che ogni misura si potesse esprimere solo con un numero naturale.[br]Questa certezza crollò quando [/color]gli stessi pitagorici scoprirono che in un quadrato di lato 1, la misura della diagonale non si poteva esprimere con un numero naturale o razionale[color=#222222]. Infatti, questa risulta avere una lunghezza pari a [math]\sqrt{2}[/math]. I P[/color]itagorici furono costretti ad ammettere che non esiste alcun numero naturale il cui quadrato sia uguale a 2.  Il carattere scandaloso di questa scoperta [b]fu un durissimo colpo per la matematica pitagorica[/b] e per i pitagorici costituì uno dei segreti più gelosamente custoditi. [br]Non mancò tuttavia un discepolo infedele che osò tradire il segreto rivelandolo ad estranei. Pitagora lo cacciò maledicendolo; il segreto era stato però rotto e il concetto di "[i]irrazionale[/i]" uscì dall'ambito della scuola. [br]Si dovettero, però, aspettare quasi 2000 anni perché queste entità entrassero a far parte del mondo dei numeri e perché, ad esempio, il famoso numero il cui quadrato è 2 diventasse il [b]numero irrazionale[/b] [math]\sqrt{2}[/math].[br]