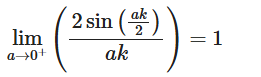
フーリエ変換をやろう
1.フーリエ変換と常微分方程式
[size=150][b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][br][/b]前回まで、常微分方程式の解法とラプラス変換の使い方をさぐった。[br]今回は、フーリエ変換をやろう。[br]周期関数の展開としてのフーリエ級数から複素フーリエ級数へ、[br]非周期の時間関数を周波数関数への変換としてフーリエ変換までの概略は[br][url=https://www.geogebra.org/m/twxxx3yq#material/rquwy3rx]周波数を抜き出そう[/url]にあるので、ここでは省略します。[br]フーリエ変換が微分方程式とつながる部分を中心にみていきましょう。[br][b][br][size=150][b]<フーリエ変換>[/b][/size][br][/b][/size][b]f(t)とf'(t)がなめらか、区分的に連続[/b]、絶対値の積分が有限なとき、[br]もとの関数f(t)に対するフーリエ変換[b] ℱ(f(t))=integral(exp(-[color=#0000ff]ik[/color]t) f(t) dt, [-∞, ∞])= ∫e[sup]-ikt[/sup] f(t) dt=F(k)[br][/b]逆変換は[b]ℱ[sup]-1[/sup](F(k))=1/(2π) integral(exp(ikt) F(k) dk,[ -∞,∞][/b] =[b] 1/(2π)∫e[sup]ikt[/sup] F(k) dk=f(t)[br][/b]時間tの関数f(t)と周波数kの関数F(k)の置き換えになっているね。[br][br]・どちらも、もとの関数にexp(-ikt)かexp(ikt)をかけてkかtで積分するところが同じだね。[br]不定積分ではなく定積分の形になっているが[-∞, ∞]証明など以外は略記する。[br][br]・フーリエ変換は積分の1種なので[color=#0000ff]線形性がある[/color]。重ね合わせの原理ともいうね。[br]だから、基本となる関数の変換公式の組み合わせで変換ができてしまう。[br][color=#0000ff][br](例) [/color][br][b]ℱ[/b](if(t>=0,[b]exp(-t)[/b],0))=∫0 dt[-∞,0]+∫exp(-(ik+1)t)dt[0,∞]=0 -1/(ik+1)exp(-(ik+1)∞) =[b]1/(1+ik)[/b][br][b]cが正で、ℱ[/b]([b]exp(-c|t|)[/b])=∫exp((c-ik)t)dt[-∞,0]+∫exp(-(c+ik)t)dt[0,∞][br] =1/(c-ik) +1/(ik+c)exp(-(c-ik)∞) -1/(c+ik)exp(-(c+ik)∞)-( -1/(ik-c))[br] =1/(c-ik)+1/(c+ik)=[b]2c/(c[sup]2[/sup]+k[sup]2[/sup])[/b][br]ステップ関数[b]θ(非負で1、負で0)[br][/b][b][b]ℱ(θ)=[/b]ℱ[/b](if(t>=0,[b]1[/b],0))=∫0 dt[-∞,0]+∫exp(-ik)dt[0,∞]=0 -1/ik exp(-ik∞) =[b]1/[/b]([b]ik[/b](+ε)) (εは微小な正数)[br]デルタ関数([b]δ[/b](x)=1/2π integral(e[sup]ikx[/sup],dx) とすると[b]δ[/b](x)=[b]δ[/b](-x)、[b]δ[/b](t-a)=∞ となるaで∫g(t)δ(t-a)[∞,-∞] dt = g(a) ) [br][b]ℱ([/b][b]δ[/b][b])=[/b]∫e[sup]-ikt[/sup] δ(t)dt=e[sup]-ik0[/sup] =[b]1[/b][br]・[b]相似定理[/b] [b]ℱ[/b](f(t))=F(k)ならば、aが正のとき[b]ℱ[/b](f(at))=1/aF(s/a)[br]・[b]たたみこみ(convolution)定理[/b] h(x)=integral(f(z)g(x-z)dz)とおくと,[b]ℱ(h)=[/b][b]ℱ(f)[/b][b]ℱ(g)[/b][br]・[b]微分変換 [/b] f→Yとする。[br][b] 微分を1階するごとにYにik[color=#0000ff]を1回かける[/color]。[br][/b] [b]ℱ[/b](f')=ik[b]ℱ[/b](f)=[b]ik[/b]Y[br] [b]ℱ[/b](f'')=(ik)[sup]2[/sup][b]ℱ[/b](f)=[b](ik)[sup]2[/sup][/b]Y[br] [b]ℱ[/b](f[sup](n)[/sup])=(ik)[sup]n[/sup][b]ℱ[/b](f)=[b](ik)[sup]n[/sup][/b]Y[br]・積分の変換(微分のs倍の[color=#0000ff]逆だから[b]ik[/b]で割る?[/color])[br][br]・変換の手順[br] ばねの自然長さy(0)=y0, v(0)=0 の強制振動の 非同次微分方程式y''+k[sub]0[/sub][sup]2[/sup]y=fcos(k[sub]f[/sub]t)[br]特殊解ys(t)を求める。[br](ステップ[b]ℱ[/b])[br]cos(x)=(e [sup]i[/sup]+e[sup]-i[/sup])/2,[b]δ[/b](x)=1/2π ∫(eikx,dx)を使う。[br]ℱ(y_left)=f ∫cos(k[sub]f[/sub]t)exp(-ikt) dt =f[ 1/2∫exp(ik[sub]f[/sub]t-ikt) +1/2exp(-ik[sub]f[/sub]t-ikt)] dt= πf[δ(k-kf)+δ(k+kf)][br]ℱ(y_right)=(-k[sup]2[/sup]+k[sub]0[/sub][sup]2[/sup])Y[br](ステップY)[br] Y=-πf[δ(k-kf)+δ(k+kf)]/(k[sup]2[/sup]-k[sub]0[/sub][sup]2[/sup])[br](ステップ[b]ℱ[sup]-1[/sup][/b])[br]f(t)=1/(2π)∫e[sup]ikt[/sup] F(k) dkから、[br]ys(t)は、g(t)=e[sup]ikt[/sup] をYの分子のδ(k-kf),δ(k+kf)にかけた積分に1/(2π)をかければよいね。[br]デルタ関数δ(k-kf),δ(k+kf)は定義からそれぞれ、k=kf,k=-kfのときに∞になり、積分値が1になる。[br]だからg(t)をかけた積分値はg(kf)*1, g(-kf)*1になるね。[br]cos(x)=(e [sup]i[/sup]+e[sup]-i[/sup])/2から、ys(t)=-πf/2π[e[sup]ikft[/sup]+e[sup]-ikft[/sup]]/(k[sup]2[/sup]-k[sub]0[/sub][sup]2[/sup])=f cos(k[sub]f[/sub]t)/(k[sub]0[/sub][sup]2[/sup]-k[sup]2[/sup])[br]同次式y''+k[sub]0[/sub][sup]2[/sup]y=0の一般解y=(A cosωk[sub]0[/sub]t + B sink[sub]0[/sub]t)がわかっていると、[br]非同次式y''+k[sub]0[/sub][sup]2[/sup]y=fcos(k[sub]f[/sub]t)の一般解はy+ys=(A cosωk[sub]0[/sub]t + B sink[sub]0[/sub]t)+fcos(kft)/(k[sub]0[/sub][sup]2[/sup]-k[sup]2[/sup])[br][url=https://www.geogebra.org/m/twxxx3yq#material/ucyjvkeu]未定係数法[/url]よりも計算が簡単になるわけではないね。
2.フーリエ変換と偏微分方程式
偏微分は多変数関数の微分、積分という文脈で登場するものでした。[br]たとえば、x,yを位置、tが時間,uが温度のとき、[br]1次元熱伝導方程式(拡散方程式)[br] ∂u/∂t=a∂[sup]2[/sup]u/∂x[sup]2 [/sup]または表式は、 u[sub]t[/sub]=au[sub]xx [/sub][br]2次元ラプラス方程式[br] ∂[sup]2[/sup]u/∂x[sup]2[/sup]+∂[sup]2[/sup]u/∂y[sup]2[/sup]=0 [br] 表式は、u[sub]xx[/sub]+u[sub]yy[/sub]=0 、または Δ u =0 (ラプラシアン:勾配の発散としての2階偏微分)[br]1次元波動方程式[br] ∂[sup]2[/sup]u/∂t[sup]2[/sup]=a[sup]2 [/sup]∂[sup]2[/sup]u/∂x[sup]2 [/sup]または表式は、u[sub]xx[/sub]=a[sup]2[/sup]u[sub]yy[/sub]=0 [br]ラプラス方程式、波動方程式は変数分離・フーリエサイン級数・重ね合わせ原理などが中心になる。[br]そこで、フーリエ変換・逆変換の流れが中心となる熱伝導方程式に取り組んでみよう。[br][br][b][size=150]<熱伝導>[br][/size][size=150][color=#0000ff]∂u/∂t=∂[sup]2[/sup]u/∂x[sup]2[/sup] 初期条件u(x,0)=δ(x)=(if x=0,∞,0)[br][/color][/size][/b](ステップ[b]ℱ[/b])[br]u(x,t)をxの関数でtは定数とみて、ℱ(u(x,t))=U(k,t)=Uとおくと、[br]・右辺のxによる偏微分ではtは定数扱いなので、uがフーリエ変換でUになる。[br][b]ℱ(u_right)=(ik)[sup]2[/sup]U=-k[sup]2[/sup]U[br][/b]・左辺のtによる偏微分は偏微分の式を関数とみて、フーリエ変換の定義にあてはめよう。[br]u=u(x,t)とe[sup]-ikx[/sup]はxの関数だから、xによる積分にからむが、それ以外の∂/∂tは定数のように外に出す。[br]今度はxによる積分はフーリエ変換そのものでUとなるから、[br][b]ℱ(u_left)=∫∂u/∂t e[sup]-ikx[/sup] dx=∂/∂t[ ∫u e[sup]-ikx[/sup] dx] =∂U/∂t[br][/b](ステップU)[br]∂U/∂t=-k[sup]2[/sup]Uとなる。[br]Uがtだけの関数とみると、変数分離できる。1/U dU=-k[sup]2[/sup] dt。両辺を積分して、log|U|=-k[sup]2[/sup]t+C。[br]積分定数Cはtからみて定数なだけなので、指数形式にするときにkの関数になりうるのでf(k)とする。U(k,t)=f(k)exp(-k[sup]2[/sup]t)となる。だから、U(k,0)=f(k)exp(-0)=f(k)。[br]一方で、初期条件u(x,0)=δ(x)から、U(k,0)=1だから、結局f(k)=1となる。[br][b]U(k,t)=exp(-k[sup]2[/sup]t)[br][/b](ステップ[b]ℱ[sup]-1[/sup][/b])[br][b]u(x,t)=1/(2π)∫e[sup]ikx[/sup] F(k) dk[br][/b]u(x,t)=1/(2π)∫e[sup]ikx[/sup] exp(-k[sup]2[/sup]t) dk=1/(2π)∫exp[ -t (k[sup]2[/sup]-ikx/t) ] dk [br][ ]内を平方完成して、 [-t (k[sup]2[/sup]-ikx/t)]= [ -t(k-xi/2t)^2 +(-x^2/4t)] [br] kの関数でない定数e^(-x^2/4t)を積分の外に出す。[br]コーシーの積分定理も使い-t(k-xi/2t)^2の積分を-tk^2の積分にする。すると、[br]u(x,t)=1/(2π)e^(-x^2/4t) ∫-tk^2 dk =1/(2π)e^(-x^2/4t) √(π/t) [br] = 1/(2√(πt)) e ^(-x^2/4t) [br][math]=\frac{1}{2\sqrt{\pi t}}e^-^{\frac{x^2}{4t}}[/math]
熱伝導
3.実装
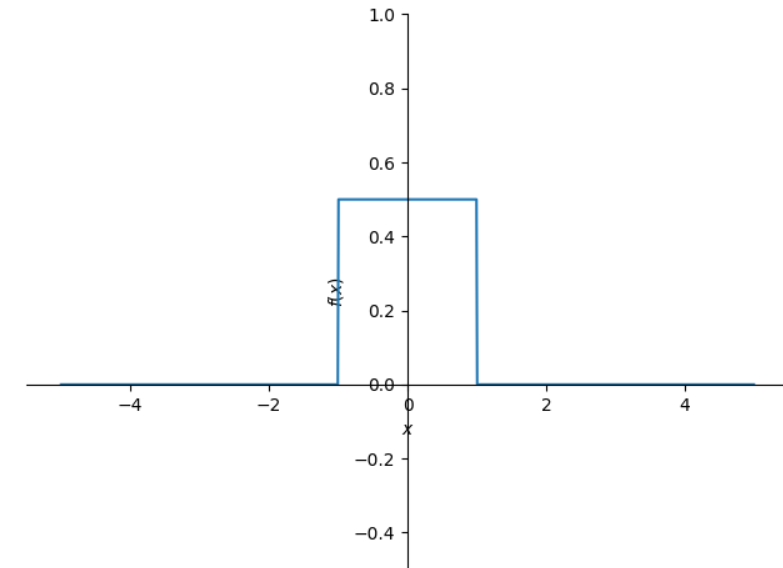
[color=#9900ff][b][u][size=150]質問:δ関数をコードで作るにはどうしたらよいでしょうか。[br][/size][/u][/b][/color][br]たとえば、f(a,x)=if(|x|<=a/2,1/a,0)という関数を作ると、f(x)の積分が1になります。[br]aの極限を0にちかづけると、f(x)の極限をg(x)にしたら、g(x)=if(x=0, ∞,0)という、[br]δ関数になるでしょう。その積分は1です。[br][br]f(a,x)はif文では変数として扱ってくれないので、Piecewise文で場合分けします。[br]var()文で、記号としてだけでなく、ゼロでない変数として定義しましょう。[br]Fをフーリエ変換しますが、いきなり∞を使った定積分はできないので、aを使って定積分します。[br]そのaをLimit文を使い、式と極限値を求め、等式Eq()の左辺と右辺に与えればよいね。[br][IN]python===============================[br]from sympy import *[br]from sympy.abc import a, x, k[br][br]def f(a, x):[br] return Piecewise((1/a, abs(x) <= a/2), [br] (0, abs(x) > a/2))[br][b]plot(f(2, x), (x, -5, 5), ylim = (-0.5, 1));[br]var('a k', nonzero = True)[br][/b][br]F = integrate(1/a*exp(-I*k*x), (x, -a/2, a/2))[br]F.simplify()[br][b]Eq(Limit(F.simplify(), a, 0), Limit(F.simplify(), a, 0).doit())[br][/b]#[OUT]================================