Bei den Funktionsgleichungen der letzten Seite war folgender Zusammenhang zwischen der Ausgangsfunktion und ihrer Stammfunktion zu erkennen:[br][br][br][math]f\left(x\right)=x^2-x-2[/math] [math]F\left(x\right)=\frac{1}{3}x^3-\frac{1}{2}x^2-2x+C[/math][br][br][br][list=1][*]Jeder Exponent der Variable wird um 1 erhöht.[/*][*]Jeder Summand wird durch den erhöhten Exponenten geteilt.[/*][*]Der Konstante Summand aus der Ausgangsfunktion wird um die Variable ergänzt.[/*][*]Der Stammfunktion wird der Summand [math]+C[/math] hinzugefügt.[/*][/list]

Aus diesen Regeln lässt sich für jeden Summand folgende Formel aufstellen:[br][br][math]\int ax^zdx=\frac{a}{z+1}x^{z+1}[/math]

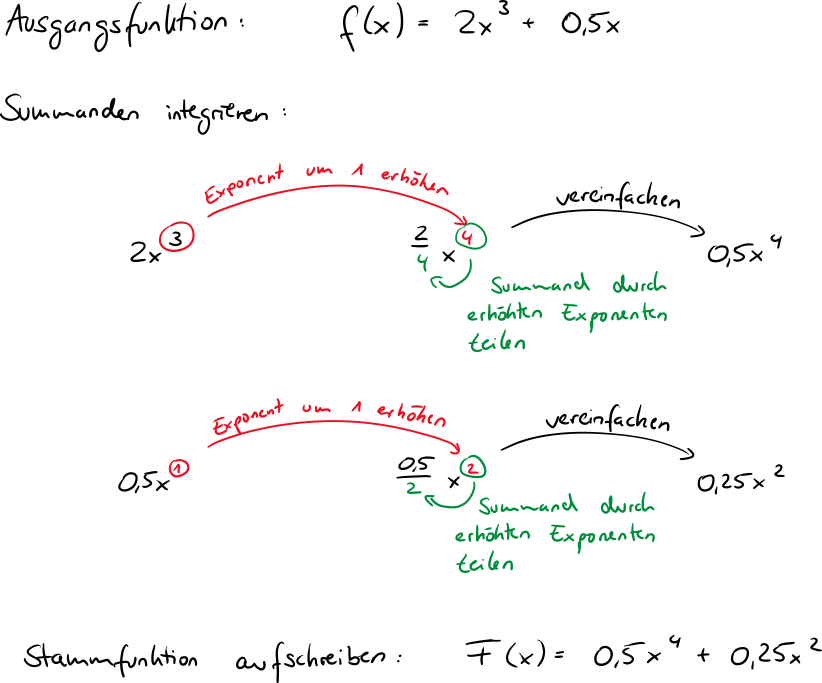
So kannst du beim integrieren eines Summanden vorgehen: