IM Geo.3.10 Lesson: Other Conditions for Triangle Similarity
Evaluate mentally. Is there enough information to determine if the pairs of triangles are congruent? If so, what theorem(s) would you use? If not, what additional piece of information could you use?
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMsAAADACAYAAACqPJfwAAAd8klEQVR4Ae2dBfQU1RfH8W8noGALBgahKHoE9dhdqKAgBraiggF2dx0Vu1uxATFQsLu70IPdiSJ67Pc/n/fn7n92dnZ2Zid24t5z5jf7m3nvvhvv++Lu7Nw2RkktoBYIZIE2gUppIbWAWsAoWLQTqAUCWqDN33//bSZOnFh1jB492lx//fXm1ltvTeW47bbbzFlnnVUlAzI99dRTAdWIXuyZZ54xDz74oHn44YcrxznnnGPGjRsX63HqqaeaBx54oNKGtPfvv//6KsF9KSvnhx56yJxyyimxynf33XdbntKG8+wrYIw333333Zq+cNFFF5k77rgjsYO+jl+efPLJqgN8CFmwXHnlleaKK66oHHSSk08+2RoNZyR9HH/88Wb48OGV9pHl8ssvt0KLoEmfn376aXPJJZeYSy+9tHIMHTrU0LlPP/302I4hQ4YYHO9s57LLLjNBwHLttddW1UPeffbZJzbZ0BN9991336p2kBUQpUWABf87++Thhx9uzj77bHPGGWckchx22GHmwgsvNGBBDvxSBZa0DKDtqAXybgHds+Tdgyp/ahaoAQvLgX/++ccuC4IsDRpJCo9GfOAh5aSsnBvxT/K+UyY/ebgnNvOSR/hIGfnfq2zYa8KLsx9JOa8y3BPZ5NyInxefNK756eFu31nWSx+579TZq5zwrQHLLrvsYtZee22z7bbbmuOOO86wn1hnnXXs5lIqHXvssfYe9zk22WSTKkDQIHU44MXBRtGPaEfKUm/33Xf3K+57r1FbvpWn38SAIo+cP//886qqtLPWWmuZwYMHG2zC0b9//6oyN998s9liiy3MHnvsYW11wgkn2HJbbbWV7aBVhUP+88EHH1gZN910U7P//vtb/gRKtttuuwqnV1991fpHfCVnKYCvsHW/fv3sXoX7+AJd8ENWCJ2c/QkZ/QjfiN+ot9FGG1X10R9++MFsuOGGZueddzbsh0466SSrM/8T6PGiGrA88sgjtnCbNm3M3HPPbT+zuXv00Ucr9Z977jkr+Lzzzms7ClEZNxFdIKJGZ4LXnXfe6S5S+f+NN94w8KIcRoDfjz/+WLkf5gOdHD6coxI63HjjjRYA8CTo4Rx5aAMdGSxwDB3NDVR4ABgcBg86Ifq5yzUjKz6BFzzFdvjqvvvuq7BDRuTi/qqrrmrOPfdc89lnn1Xu8wEZqUMZjgsuuKASGawqGOAf2pMjQPHARZBxwoQJVr655prLHHDAAXXr0r7Ym4GKzv/6669Xlaef45errrrK8sR/lPPzTQ1Y4Pjtt99WGNCwk6ZOnWq6detmIzA///yz81bN50MOOcRGLnAAkQwvgv+gQYPMTjvtZNskEheF4Ed7brmb5XnMMccYoiLw7NKli3HrDHgGDhxY4wxne8iCzeAxadIk563In2mfjgPvu+66q4of9w499FDTt29fQ7TPj7766ivLA0D99ddffkU979HWa6+9Zvbbbz+z+eab23a//vprz7JcZFAMO2AwEACCrl27GmZm2nQT14iY4Tdsctppp7mLVP0vtmPQa0SeYKEiDR188MEVgRDi/vvvN8sss4y5/fbbK9frNUB5lgdvvvmmmW222QwhUy/lQDZLl8UXX9y2+fLLL9djGeh6nGBBXpaj6CAz5MiRI6vkoL2ePXv6gpNRDXsyesUFYhFC2oe/c8Z4//33zbrrrmuXF87wp9RznwnVwuPAAw903wr0P6sNgMYyE9DKbPfYY4956jzffPOFBiUgYJnJkorBx8uWL730kmnXrp3ZYYcdrD701XrktB2DRSOqAQsdZLfddrMNsQSBMDYxeIzJGjgIUWexxRazBgFgdBQ3WFhzAxKWYfCuZ4Ag7UkZDAAvL0NKmaBnloI9evSwvJi24bviiitW8f7www/NjjvuWKObsw3piCyH4iYB4gorrFCRiy/vkBX/BbGD0+csQ8ISbcwwwwwGGzmJmQU5zjvvvKrvK55//nnTq1evQLIJP2TcZpttzNtvv233f14+Rg5mUb5YXHLJJW3bkydPFhY1Z+l3QQexGrDQIJ124YUXNu+8845V6KCDDrLT2rRp02oarHcBg7BZAjTrr7++6dixY5XBaIf7rBuvueYaqxggjUrw9TJkM3x5goBpH0fBt3Pnzpb3TTfdVGHHLMw+oB5F7Yj1+Mp1AeKuu+5q5eQLRHyHXYOS+By7TZkyJWi1Sjnq05E5u4kOybKMPsCXvAwY7du3t3sFd1m//+lHAIDziSeeaP3Ass9JLPVZCbz33nv2PgMx9q9HYjvnCqpeWa7XgEVGKpTis2yUaJj9SlBCcECAsDgSR6Co0J577mlHF+7zLTT3+cY2KuGwuMDCN7k4Roj1L7wZvZCbgygXI1k9QmcZfJz61ysf5jq6yiqATTn7gJVWWsnKyEogKInPl156ac8O34gPduBpgnqEnOw3eErj6KOPNiy1qROGsDG2pp4MrsygQi+88IKR2ZUZFT+xF65HTtvJCqpeWbleAxZBGyMm4URQSoiNxv0MIgw5o9DWW29tJNQq0RjpLKwPl112WbtEQ2hxMKNQVIJfHGBBBx6BeOuttyoisQSAN8ezzz5rOxZA+P333ytl3B+kIw4YMKCpjujm5/wfXbt3727lWW655ewjIuypkI9ljtjbWcfrs/icASxJwqYczRADlczoRK3Qkf0LBE8ity+++KL9H1Byn8eK6hG2w3eU++ijj+oVq7peBRYalZGKjgJD6OKLL644IEikhBlo/vnnr9RnzYpQ1IUncX2CBdAvv/xi7yF4s4a0jKb/gT9tiezOe2E+//bbbzbw4OSDfHynAn82wn/++acdvfzklo5IHN+LsDeb4WZIgMjAI/sFonUSLAkyuDl9fsstt3iKwcDXKHLFgBj2cNrWs+HpFylHCPjLL7+0V1h+4QOCRhArAPyBLpRlD8J9v8FXbMeg4tWnGRjd++wqsNCQoO2bb76ZLqoxzAQygo0ZM6Zyvd6He++9t+qLSkYEhKdz0TGcwJBRIo79CvKgA21xjkJM+2zm3UCg08B/gQUWMER6iNDUI2dHdId1qYOM7NuCjmzudgSIDGxOkpl8gw02qJHfWY7PTp9//PHH7tt26b3aaqs1nKXqAQV/83AmMx4jPQcPhLKECuqj77//3sw444yV8kT98MHGG29sl8CrrLJK5R59lVmG8LLbd07lxHaEjr3K8fAwexknVYGFsBtCECZ1T+GMUtyTjaSTifszziMoIMQsQl0iEyjm3ESeeeaZ9t4NN9wgxSOdcQBtBXVEvcZwqNeyBMMS46cNdOGx7nqEDCyPKMt3V26iw2y22WY1sno5z12XMjxtAW8GJyd98skn9jr3ZGnivO/8LD7v06dPjRyUo7OzFwoik5NvnJ/5QpsvfoVY9qIbUVbOfGEpJF8y8kRDPUIXWSF4zabMNOutt17Nd1NVYGFTTuPDhg2raYdRh3sdOnQwn376ac19uYAgvXv3rnKgrPVB6qhRo6SodQ7RC/h+9913letRPsQBFjFmvRg915G5U6dOniAQ+YmmUc6rI7KUWGqppcz5558vxe2ZjgkICKv7EXqy3FpkkUVqOjn3WKLQNiO+X0cXn3t9v0JHgge/9WlEtBH2aMRT7tNHnJ0a/RZccEEz88wz20ib6MeZqBwy+z0xIrajnHs2ZZLgez/4CF+Rw4KF5QSjHOiFAaM8oUeYQlQCsYT8uI8DWFY4mfEZHvwWQspIzP7XX3+11/baa6+KQXm8giWYPObC6Og0iAjod4a/+5BlHWf3Pf53yuzmzb0nnnjCPsLi1sFZFrswq2y55Zae/Fiq0b4shwCAyMIP65h5WdbOOeecdokrvGlfoo90YrG/3OfMF6TYCv8gI+Wxu9N2tEUb3J9jjjns0se956AMj4+Iz+FHGY7rrrvO7L333rY+63b3KsMpj3ymXNij0YDAjwIZYNGDDkxYHMJODMjsN9ij8f/48eMNWwSxH4OyO3xOOfwitmMQ40eG2AK9WS6KPVimuakNazznelN++MIZ5hCbRynDYylffPGFjXQ5jShlcBKPf8j0TX2cTn3qQTickYwyGEB+5EObYYgH4JgFCSkSJsSgchDJIyTtPkQnr3YwGMEH0YFHJpDRiwA7OnkRI6HIwZkpn0d/jjjiiIodxZ5ueQAC93C6+x5tISMDEnIxK4m/GMyEmJngwewisjjBRDnqc4gcnOV/Ocs14et3lg6HfEEPL/2kDe6xlEIW7CcyyQCCbBIkoqzozBME9foTcjn9wucRI0ZYv8Bf2uDstWyuWoaJoHpurQVYvjEo+XWm1kpYztYVLBn0O1EeZiKlbFlAwZItf9j9Aht3WW5kTLxSi6NgyZj72c/5fZmWMXFLJY6CpVTuVmWjWEDBEsV6WrdUFlCwlMrdqmwUCyhYolhP65bKAgqWUrlblY1iAQVLFOtp3VJZQMFSKnerslEsoGCJYj2tWyoLKFhK5W5VNooFFCxRrKd1S2UBBUup3K3KRrGAgiWK9bRuqSygYMmpu/mxE79MVErPAgqW9Gwda0u8HZOfKyulZwEFS3q2jq0l3o7D79LHjh0bG09l1NgCCpbGNspcCfKyAJZm3zeWOYVyIpCCJSeOcorJ8otlmFK6FlCwpGvvWFpjY8+L/pTStYCCJV17x9Ja27ZtdXMfiyXDMVGwhLNXy0uzT2G/4szx2XKhSiKAgiVnjiYCBliU0reAWj19m0dqkTd5ksNSKX0LKFjSt3mkFtnc814xXlPqPDSMHMmsgSorWAKZKTuF6r18OzsSFlcSBUtxfauaxWwBBUvMBlV2xbWAgiWnviXPC9nYnAlic6pKbsRWsOTGVf8TdNq0aWbVVVe14WNCyByk9VZK3gIKluRtHGsLZD0WkMh5rrnmCpSdK1ZBSshMwZIzp0vORAGKnPXN+8k7UsGSvI1jbeH000+vmVnIy6mUvAUULMnbONYWyOPZrl27KsB4ZZeOtVFlZi2gYMlZR7j66qstUNZcc00z44wzmuWXX95m7c2ZGrkUV8GSI7f9+eefplOnTjb99IknnmjzwN9zzz0WPCNHjsyRJvkUVcGSI78dddRRFhjPPfecEbAg/oABA8w888xjvvvuuxxpkz9RFSw58dk777xjgUJueMgJlnfffbfqXk5Uyp2YCpacuIzZg19IyuzhBAsqOGednKiUOzEVLDlwmde+xA0W9jOLLbaY2XjjjXOgUT5FVLDkwG8rr7xyTcTLDRbUuOaaa+xy7KabbsqBVvkTUcGScZ8R5eJb+rvvvrtKUi+wUGDdddc1Xbp0qSqr/8RjAQVLPHZMhAv7E/Yp7FfcVA8sjz/+uAUXv6JUitcCCpZ47Rkrt6FDh9qOTyTMTfXAQrm99trL1vvggw/c1fT/CBZQsEQwXpJV+S6F5RdRLi/yA8sXX3xhZpttNrPzzjt7VdVrTVpAwdKk4ZKutskmm9jo1h9//OHZlB9YqHDGGWdYsE2YMMGzvl4MbwEFS3ibJV6DaBazCs+B1aNGYKFejx49zGqrrVaPhV4PaQEFS0iDpVF86aWXtlEtv7aCgOXOO++0oOPnx0rRLaBgiW7DWDkAAmYVolp+FAQs1OcF4h07djRTp071Y6f3AlhAwRLASGkVIXo1wwwzmD333LNhk0HB8tprr1nwDR8+vCFPLeBvAQWLv31SvUv0iijW559/3rDdoGCB0YgRIyxgXn311YZ8tUB9CyhY6tsm1TsTJ060HZooVhAKA5ZffvnFzD///KZv375BWGuZOhZQsNQxTNqXV199dRu9CtpuGLDA89JLL7VgvOOOO4I2oeVcFlCwuAzSin+JVrGpD9ORw4IFvQBk9+7dW6FiIdpUsLTYjUSpWCKFTXvXDFhkqccbYpTCW0DBEt5msdZodvPdDFgQfPDgwWbWWWcNFESIVdECMFOwtNCJRKdYfgGYsNQsWD788MPA4emwMhW9vIKlhR5m6cUSjGhVWGoWLLRDXUD62GOPhW221OUVLC1yP5t5Omyzj6JEAQsq80jNOuus0yLt89msgqVFfuMhR6JTzVJUsIwaNcqC1e9hzWZlK2o9BUsLPCuPzxOdapaigoV2G/0MoFnZilpPwZKyZ3mUJY4fZsUBlueff97OLkceeWTKVshncwqWlP3GQ5I8LBn1J79xgAXV/X66nLJpMt+cgiVFF8nLJOjoUSkusHz//ff2pRjbbbddVJEKX1/BkqKLeU0RUag4KC6wIMt5551nl2Pu1y3FIWeReChYUvKmpIqI6wV4cYIFE3i9yC8l0+SmGQVLCq7ipRO8WpXoU1wUN1jkFbHnnntuXCIWjo+CJQWXJvHS7rjBghkGDhyoqSt8+oOCxcc4cdySVBFEneKkJMCiqSv8PaRg8bdP5LuSKoKoU5yUBFiQT2bBZ599Nk5xC8FLwZKgG4ku8fxXEinskgLLX3/9ZVPxaeqK2o6hYKm1SWxXiDBxJEFJgQVZNXWFt8cULN52iXxVUkUQZUqCkgQL8q633nqausLlOAWLyyBx/OuXKiIO/vBIGixPPPGEXUJq6or/e0zB8n9bxPaJJKnsVbxSRcTVSNJgQU5NXVHtLQVLtT0i/9coVUTkBqYzSAMspK6YffbZNXXFdJsrWOLqvdP58C19p06dDAlRk6Q0wIL8Z555pp0lNXWFMQqWGHt0kFQRcTWXFliQV1NX/M9rCpa4eq8xNnrEk8VpUJpgkdQVF198cRqqZbYNBUtMrqHzsqlvlCoipuYSj4a55dx6661Ln7pCweLuFU38z68eAQrRo7QozZkFnTR1he5ZYunbkiqC6FFalDZY0OuQQw6xg8Irr7ySlpqZakdnlojukPcHB00VEbG5SvVWgGXatGlmgQUW8ExdMW7cuIpsRf2gYAnhWa9HV0hwSrQobWoFWNDRnbrijTfeMP3797czzhVXXJG2GVJtT8ES0Nynnnqq7RC82OGtt96ytSRVBNGitKlVYEHPNdZYw3Tt2rWyLJtvvvnMBRdckLYJUm9PwRLC5LzYoX379hY0Bx10kI0OhU0VEaI536KtBMuwYcOsDQhqHHzwweann37ylbUoNxUsIT05ZcoUA1DoKBz8WKoV1AqwjB8/3vTu3dvqzVMKs8wyS6lSVyhYmujpkiqiS5cutuP06dPH3H///U1war5KmmBhgNh+++2trj179jRjxowxpK74z3/+EyizcvNaZqumgqUJf7D0IipEqojRo0ebFVZYwXakQYMGNcGtuSppggUJWW653/xy0kknWb3LkrpCwRKyr0qqCKJCTjrnnHNMmunn0gaLU1fn5zKlrlCwOD0f4DMJTKOkigjQRKAiWQGLpK646qqrAsmd50IKlhDeiyNVRIjmfItmBSwIuemmm5pFF13U8DLBIpOCJaB3SRVB4lISmGaBsgSWsqSuULAE7PmkiiD6QxQoC5QlsGAP+e7l7bffzoJ5EpFBwRLArHGmigjQXKAiWQPLDz/8YNq1a2eKnLpCwRKga5KoNK5UEQGaC1Qka2BB6KKnrlCwNOiakiqCqE+WKItgwT6rrLKK6dWrV5ZMFZssChYfU0qqCKI9WaOsguXee++1X1S6v8DMmv2akUfB4mM1EpPy/BevN8oaZRUs2ElSV3z77bdZM1skeRQsdcyXVKqIOs2FvpxlsBQ1dYWCpU43JVUE0Z24U0XUaS705SyDBWWOPvpoOysXKXWFgsWjm0qqCKI7WaWsg6WIqSsULB5oIJqTVKoIj+aaupR1sKDUtddea2eXG2+8sSkds1ZJweLySNKpIlzNNf1vHsCCcqSuWGqppZrWM0sVFSwOb5AqYp555rHRHMflTH7MC1iKlLpCweKAgqSKIJqTdcoLWLDj3nvvbZdjkydPzrpZfeVTsEw3T1qpIny9EeJmnsDy5Zdf2tQVO+20UwgNs1dUwTLdJyQcTSNVRFxdIE9gQecipK5QsBhjJFUEiUfzQnkDC3ZdfvnlDS8lzCspWKaniiBqkyfKI1h4uQePD+U1dUXpwUKCURyYVqqIuACZR7Cgu6Su+Pnnn+MyRWp8Sg2WVqSKiMuzeQVLnlNXlBospIogwWiaqSLKDhb0z2vqitKChYSiLL+I0uSR8jqzYGu/1BVZ9kVpwdKqVBFxdYY8gwUbXHbZZXawuv322+MySeJ8SgmWVqaKiMujeQcLdiB1Rbdu3eIySeJ8SgeWqVOn2lQRRGXyTEUAy4MPPmhnlzRfexvF56UDy/Dhw62DiMrkmYoAFuy/yy672JcXfvbZZ5l3R6nAIqkiRowYkXnHNBKwKGD56KOP7MsL99hjj0Yqt/x+qcDSt2/fSqqIlls+ogBFAQtmyEvqitKApV6qiIh9tmXViwQWjLjMMssYXmaYZSoNWEgVQfSlKFQ0sNx88812L5nl1BWlAAvRFr6AJGd9UahoYMEvkrri999/z6SbCg+WrKWKiKsXFBEsWU9dUXiwZC1VhILF3wJZTl1RaLCQGJTlF9GWolERZxZ8lOXUFYUGSxZTRcQF2qKCBfucf/75dpAbN25cXOaKhU9hwZLVVBGxeM0Yw0vLZ5ppJvP++++HOvgNTx6I1BUrrbRSpkQtJFhIFUFC0CymiojL+0OGDLHffO+zzz4mzHHbbbfFJUKifLKYuqKQYJFUEURXikoCljD68Vh8XsCCXttvv7196WFWUlcUDixZTxURpnP7lS0DWCZNmmT3Lvvtt5+fKVK7VziwkAA0y6ki4vJsGcCCrbKUuqJQYMlDqggFSzgLkLqic+fOhpcgtpoKBRZSRRBFKQOVZWbBl1lJXVEYsJDwky8giaKUgcoEFvyZhdQVhQBLnlJFxAXksoHlySeftIPh8ccfH5cJQ/MpBFjylCoitIfqVCgbWDBDq1NX5B4sJPhk+UXUpExURrC0OnVFLsFC/J23s8w999z2S6sOHToYoiZlIV7l1L59eztIDBo0yHz11VeBVM/bl5JeSslPkOecc07760r2qmlRLsGy4oor2o7CjCLHU089lZbNWtrOXXfdVdFZdF9//fUDyVQEsGy11VY1+qeV4DV3YJEfCElHkfNCCy1kevfuXfijY8eONZ0FG/As3OKLL97w6NKlS25tRAZp8bfzvM022wQaLKIWyh1YXnnlFU+DLbfccqZ///6FP5ZYYglP/fmOqU+fPg0PfraQVzvxdh4nSOTzwIEDo+IgUP3cgQWt1l577Rqj5f2leYG8ZYx5+OGHa3Tv169f0Oq5Lzd48OAa/VmapkG5BMuPP/5oeLiO2WSLLbYo1Isogjh9zJgxZqONNrLvCeaFgX///XeQaoUpw1PlPXr0sF9U8laYtCiXYEnLONqOWsBpAQWL0xr6WS3gY4FcgoX34/LeYjdxjZdUFJnQvZ6OU6ZMqXuvCDZ59NFHffUT23j1jTj0zyVYiLVzOEmeTOVcZOKt80SB6DhuQve2bdu6Lxfif3mpO7rXIwn8YKMkqH7LSbQWE09+3+B8oK4sQMF86A4gvDoE1+gwRSR8LGDwGyiwzciRIxMxQe7AwlTrHFnLBBSWWegOKPg1KP87qWfPnlWDiPNe3j8feOCBdjXBYOEFFhlAnX0jbp1zB5axY8faDkNHKRNQcDydRJYhjKDo7yTuYZ8ikgwEzC7OVQW6MpMAFukPSemfO7BgKAwnhnF3mKQMlQW+ojuyMNLyjJyQAMk928j9vJ9lIGBWdYIFfZll0R+bJLkMzR1YMAbGwXgcRe0cXp2boIbsVWTDy7IUogMxuhaRnAMBejoB4fyfQRTAJEW5AwsAwViAhKWIc5RJykhZ4evevDo7h1eEMCtyR5VDllnwYSUhYJH9q4SK6RtJrjRyBRYZTRlpIIDCk7ZlIHfHQGc6kejPrJJUFKjV9nUOBDLLIBOzrMy0cl2Ak4TMuQKL7FPEENKBkhxNpK1WnyWw4ZSD2ZXRVO7JIOIsU4TPzoFAdAYUzLSyDGWgwBZJUrLcY5bcawPHqJP1XIRxmMFLd/iiP7NL0h0lDh2a4SHgcA4E6Mq+1bkExw6yPGumnSB1cgUW5xpdlJNRNcnpV9pq5ZmO4LV5Ff2xTRFJlldO3dCVWQUgCTH7OMEj1+M85wosGMM5wogh6l2X+0U4o2O9AYF7RV2K4m/3Xgxd3f3Azz5x+T9XYIlLaeWjFmjGAgqWZqymdUppAQVLKd2uSjdjAQVLM1bTOqW0gIKllG5XpZuxgIKlGatpnVJaQMFSSrer0s1YQMHSjNW0TiktoGAppdtV6WYs8F9A/3GZhV4OjAAAAABJRU5ErkJggg==[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMQAAACwCAYAAABQFcG8AAAej0lEQVR4Ae2dCfhNxRvH2zxJmyWhxT+ytShEKtJKIklEZSeytaAs7ZvsLbaoECqJSpRIhLK1U1o8FBWilKIVzf/5TL+5jvM7995zzp1z7zn3zvs85znbzJyZd97vme2d9z1AGDIcMByIceCA2JW5MBwwHBAGEEYIDAcsHDCAsDDDXBoOBAKIVatWOXJ27969wu3hmEAIHv77779i4cKF+XLC8z179sSOf/75J3ZtfZ4vonkQKg5oB8S7774rLrroIoGAWAkgHHDAAa6PBQsWWKOH4hrBbtq0qXjhhRfy5eeuu+5KWrYrrrhCvPrqq/l4ky8x8yBjHNAKiE8++USUL19evPXWW44FQqDefPNNKTgXXHBB7A+6e/duwcF7JVhffvmlYxrqIQDbtm2b+O6772Sro547nXfu3On02NMzAN69e3dBvvm2nXhPGXgP8P/++29ZHp4Rft26dRJMvHMClD09c58ZDmgDBMJJZU+dOjVhSYYNGybDdenSxTEcoCAdBCkeEeaWW26R4Qh75ZVXisWLF8cLLho2bOgoxHEj2F4g7HfccYcU6ET5QvALFy4sSpYs6fi9b7/9Vhx33HGiWrVqEiy2z5jbEHBACyAQhDp16kgw2LtK1jLyrnHjxlKQn3322dgrulmqX05ap556qqNAEYH3M2bMEPfdd5/4+OOPxffffy9efvllmebzzz+fL95HH30k6KoQzy9NmzZNlg8gJqIPPvhA5qNmzZpxu0Vt2rSRYcizofBxIGVAIGh0JfjjJwIDRUeg+IMWLFhQbNq0KcaNyZMni5EjR8p70qDbES8t/tCjR4/OJ+AMYv/3v/+JgQMHxt6Rt3vuuUeQvl9avny5OOKII2SXJ1kajz32mBT22267LW7Qvn37yjC0lIbCx4GUAIHQPvjgg7JLkqgroYqt/qD8sQEHAkvrQIuwZMkSFSwuGAiwceNGMWjQoFhY68Xq1atlC1SuXDkJhEaNGolmzZol7H5Z49uvN2/eLE488UQ5ELa/s9/DixYtWkhhjzeGIk779u1lGMBjKHwcSAkQDA7POOMM2W1xU7Thw4dLYaDfTxerdOnSsfsdO3a4SUIK92effRY3LECjO0LLMGXKFN99dcBKHuOBz54Bvgt4ACNxnYjnDRo0kGWeM2eOUxDzLMMc8A2Id955RxQrVkzMmzfPVRH4g1599dVSGJhpootDq9KzZ09Rq1athK2Cqw9oDITgdu3aVTRp0sR1vtavXy/L1rFjx7hxAE2RIkVkuA0bNmjMsUlKFwd8AYIpxNNPP11MnDjRdT4QslKlSklh2L59eyzeiBEjYn9hQPPAAw8Iuj7xiDD8/Z2Ofv36iV69eskxTadOnUTbtm3FddddJ+6+++54yeV7Tvp0A6tXrx73T58vkhDimWeekWUbP36802v57LnnnpNhAFq8ViRuZPMiLRzwDIg///xT1K1bVwwePNhTBteuXSuF4cwzz9zvDzphwgQ5LiAxhKRGjRoJhQWBfemll8TcuXMFrdSKFStiBwNg6726drvIR9oIdIkSJRLmwV5w4t1www2yfPHWT2gdLr/8chkm0RjDnra5Ty8HPAECgb3++uvlXxgh8EJPP/20FIZ46w+kxV/fy9/cy/fdhJ01a5YoUKCA+Omnn9wEj4WBL5UqVUo4fujWrZssf4cOHfb7IcQSMReh4IBrQAAAFsMAhFcwEJ54DKYnTZrkWHD+4rznr54JWrZsmVxQW7NmjefPM1NG3tu1a5ePN4BFrZPceuutnloezxkxEVLmgCtAINDM71esWFEOhmn+1ZFIiY14CPr8+fNF0aJFpdAwCOeebgPH9OnTZcuAQDHoTgY2VsRpZawHU6sADoHs3Lmz6NGjhxys9+nTR6qCoA5iXfewc42p3MqVKwtaCFWuZGfSeO+99wTdNFo28s+ZMlG+V155RTz++ONymrVs2bJizJgxBgx2xofw3hUgyDeLZepgOlId559/fuxaPePMnxHBUHGsZ95b79U1im/JCMCgHmI9iJfsSJQuK9EqD5yt5XC6HjdunEzummuuEWXKlNkvrjUdrkmbcZehaHDANSAQRC8HxVfhAYe65my/t77LBNus33d7rcpHWVR51Fmlwb2haHHANSCiVSyTW8MBfxwwgPDHNxMrSzlgAJGlFWuK5Y8DBhD++GZiZSkHDCCytGJNsfxxwADCH99MrCzlgAFEllasl2KhgXDhhRfmO9iRmGtkAJFrNe5QXnYasoh477337nf88ssvDqGz+5EBRHbXb9LSffPNN1Lt5O23304aNhcCGEDkQi0nKCM6V+hh5WJr4MQWAwgnruTQM7pJdJkM/ccBA4gclwTGDlhCsQ6qMRWUq2QAkas1n1fuo48+WloqsQ6ovWwNzjb2GUBkW416KA/TqowfzIB6H9MMIPbxIueuaAkAhKF9HDDc2MeLnLtiQQ6jD4b2ccAAYh8vcu4KMFx11VVi0aJF+x05xwhLgQ0gLMzItUu6S05HrvHBWl4DCCs3zHXOc8AAIudFwDDAygEDCCs3zHXOc8AAIktFAEuJVatWFcWLF5c2br1aI8xStiQtlgFEUhZFL8Ds2bPzDZYvu+yy6BUkAzk2gMgA03V9EquJuBRjxRkXA1gXf/TRR6XPDqfZo9tvv108+eST0qrg0qVLBQaojZbr/rVhALE/P0J799tvv0kVC1xxYeK/QoUK+VoBQHDYYYfJwwkQRx11lDjooIPyxeP5pZdeKh1LYocWdwe5SgYQIa157MaOGjVKmtk/66yzYoJcqFAhqZmK00l0kHAqiQD/+OOP0u4uxVGuj62gwFOrIsBFy4JhZ2zTYoAafxqnnHJKDCx4Q8KPBd8BJH/88YeKntVnA4iQVS9uylg9VsKMrwp85eHExa0SnnLseOyxx4oDDzxQGn92a18Wv98vvviiNBZ9zjnnxPKBqzCMRidyZxYyVvrKjgGEL7bpjcQ2zocffjjW98eXNZ6QMNHvlXAmA5iwfH7//fdLfxde07CGByA4talXr55Mly4XltYZuGcjGUBksFZxFYDnIdz+IsS1a9eW3SS/U6Q4hmealc0+kA5AWNmDzhNuCNhDQX5pQTD5v3XrVmuwSF8bQGSg+r744gvRqlUrKVR4LMKZuw6vpA0bNhSMMZRbL92AUKwCeEOGDJHrHACDLajKRYAKE9WzAUSaaw7/1PzFmQ1iwKqEN9VskBbCaXVSHxQgrHmdMWOGnKHi2zi8+fDDD62vI3dtAJGmKsNBpHK62Lx5c4ETe130+uuvSzDcdNNN+yWZDkCoD9J1Yuxz+OGHy/GQeh61swFEwDXG7A6zMwxGcWVs/YPr+DTTraVLlxY1a9bMl1w6AcHHv/76a3HjjTdKcGK8gOnfqJEBRIA1NnPmTOlmGDD0798/kFXhpk2bSrA5mZ1MNyAUK1977TWBqzW6Ub17946USzEDCFWLms9jx46VAoFJF9QkgiB8hSN0qGMoso5JMgUIlRcG3kwaXHTRReKrr75Sj0N9NoAIoHoeeughKagtWrQIIPX/kly4cKH8BjNUihC6QYMGqVvt066xhD1cML4pVaqUOOmkk6QTTg9RMxLUAEIz2/FFzV/7hBNOELjjxY2wbtq1a5d0kYyQYSgAb684eMTFMQKoKNMthMoH6iWMn+DL+PHj1eNQng0gNFULmqcsrFHpb7zxhpx+POSQQ6TahaZPxJJRaxisZLOSjJDddtttAn/dqHf8/fffMmxYAKEyzoIh/GGKOKxkAKGhZjZv3iwKFiwoD2sfnhklBKBfv34avvJfEiNGjJBpMs1pJaZxAcrw4cOl7hIzW3Xr1k1ZdcP6DR3XTALAkw4dOuhITnsaBhApspT1BSoYdWxaCTspRbspU6bYX3m+RzOVb7Vs2TJf3FmzZsl9DuoF07E9e/YMHSDI34ABA2Q5UDkPGxlApFAjGzdulBV77rnnJkwFlQpmW+hL+6U9e/aIKlWqSODt3LkzXzIImX0fQ9i6TNZMz5s3T/LOvphoDZOJawOIFLh+5JFHimOOOSZpCii/MQBmj7Pq3yeNZAvAfgVaBxQCnYixhJ3CDAjyyg4/ysR+jLCQAYTPmsDqHZXpdhZJTZPSz/dKrDPwLeuUqps0wg4IyjBw4EBZtrCsahtAuJEsWxh2kiGgXjVUR44cKeMhBG7pk08+EQcffLBUnHMbR4WLAiDIa9euXSVfUulSqjKnejaA8MhBNu4ABlaJ/RD7CYjPINgNseeA7ZxuWyJrmlEBBHlmnMWuPFTLM0kGEB64zx5nhJndaKkQ6xWMPdavX58wmZtvvll+z7rYljCC7WWUAPHDDz+IypUry6ni33//3VaS9N0aQLjkNbvFAIOO+XPMvxQpUkS6wo33eaZp+R6effxSlABBGVloZDdeu3bt/BY55XgGEC5ZePHFF4s6deq4DJ08mPL+2b1793yBWdxjW2mDBg3yvfPyIGqAoGysuvMj0K0m75ZvBhAuOKWU9XTPhKh0x4wZs18u0A6lS8U6RyoURUBQXqyOMJ7YtGlTKsX3FdcAIgnbWB0+9NBDBVbvgiCMjvFHvPbaa6XeE2Dgnq2ZqVJUAQHPmVljs1G6yQAiCcfZ9skK8a+//pokpL/XLKixig0I1FG+fHl/idliRRUQFOOOO+6Q/Jg2bZqtVMHeGkAk4O/QoUO1/a3jfeaRRx6JAUEBgrOOOfkoA4IfELNOp512mrRKGI9/up8bQMThKNYjUM0Iutlma6kVCOqaPQ6pUpQBQdmfffZZyZt06jsZQMSROrZ+ssHHSUcoThRfj9966618gACIfnWerJmIOiAoC7sO+UmwTzsdZADhwOUVK1bISmAhLh3EqjcWuKl4zLgwpkBlI1XKBkBg9Bm+WLfKpsqXRPENIBy4g3oGC2dbtmxxeBvcow0bNghWbLGEV61aNbF79+6UPpYNgIABTMOyAcuu3p4Sc+JENoCwMWbHjh1yPzQ2VzNFqhvVunXrlLKQLYDAIjqtBAahgyYDCBuHlao1+6IzSWwRRQi8qnxb85wtgKBMZ5xxhpz+tpYviGsDCBtX2dZYvXp129P03OLeqnDhwjEdp86dO0tQ+B1QZhMgaB34QeC8JUgygLBwd8mSJWlrmi2fjV2iyIdyG7vrFNWqVUvg+AQfEl4pmwBB+dHvYkU/SDKAsHC3R48eUmUgE1bmqHBaB0DBn1AReeE5Kh1eyQ8gyAeavRxhc8jIuA6zoJ9//rlXVrgOv4/zrqNkZ0D8rvEnxjJ3Jqht27ayq4RdJQBhbRGUVyAA64W8AALtW2U3ie+rA6+mYSH2k5OvIO06GUDk1baa2cmEZTkMFVPRgIG/srq2CuIDDzwgnz/xxBPWxwmv3QJi4sSJMm0WI61ABCTW+4QfS9NLHEMG6XPbACKvItWgDe8+6SZMx3MoAhAIqZ3Uqi22oNyQG0AoMIapJUhUNjYPsYjp1olkorSc3hlA5HGFxR8UydJNqov0zDPPxPruDKqddsqxtRIbqWjD/vzzz0mz6gYQABELIlEhZVVdh66XU5kNIPK4wsAVAwDpJmXOhlbBejCmcCJUGXC1C4CTUTJA0B2K1xolSztT7xlQk+egxhEGEEKIlStXSiajXZlOUn13ez9dDbDj5QU3uQjFnXfeGS+IfJ4MEHSTSCdss0kJCyWEVLoMahxhACGEUIKBS6h0EjpLmLO3E90l61qE/T33eOZBmJ9//nmn1/JZMkDYp3jjJhSyF/jJZhwRBBlA5CmPnXzyyUHwN26aCCOLcE5/Z9VyxI2c96J+/frSm+mqVascg7oBBF3FqNHTTz8tfwZ0H3WTAYQQcuGrffv2unkbNz1AoBbhnAKpgba9K2UPixl+jJihaoLDFDu5AUQUu0y05OQ7iJmxnAcE3nhgrhfzknbBy+Q9sy3k32kQngwQalDtNKOVyTK5+XZQhh9yHhD8ZRGo0aNHu6mHUIZRYyCcHFopGSAIyxiG8jNrhVN5Zm9wC+a0DmJNO9PXaBUEsb035wGBUTAEIt0zTLoFCj0fymE1e+kGEOSDFWlWqdUCIdd028JM2G3ChI9uynlAqC2Ks2fP1s3btKeH45aSJUsKdt5BbgGR9oxq+OBZZ52VsmVDp2zkPCCUDtPixYud+BOpZ6idMB15ySWXyHxnMyAwLYrRaN2U84BgwwldDR2b+nVXjp/0sPhHebAcfs899wg8oWYjMeZhF51uynlAqDn/dC/K6a5Ia3oMjAEFKh6czz77bBHEnL31m+m+ZlYt2eKlnzzlPCDU3uXt27f74V8o4yiQAwZ1REmBzw1TMV5WtGhRN0E9hcl5QDz44INSaFI1+eKJ6wEHVgaUFRjUORM7AYMqKn64g+gO5jwgmLtHYFigyxZSawsKCOqM7+psIayxY9RNN+U8IJR+fSZ8EeiuTJUeEwT8PRUQODNNmU2ERZJSpUppL1LOAwJtUQQmEzvltNemJUGsh9esWVNuymcaljJi8CtbiN2DFStW1F6cnAcEK7sIC/Zcs42s6xD16tUThQoVEp9++mlWFBO/HTVq1NBelpwHBPuTAYRud1naa8pHglZAfP/99+L444+XQvTvv//6SC1cUc4777zYAqTOnOU8INhLACCmT5+uk6+hSMsKCDI0b948WdZ0qroHxQj2ljdp0kR78jkPCKUCnQnzM9pr05agHRC8Vh6Lhg0bZgsdrVv2gQThvjfnAcGCHC0EgpJt5AQIytixY0dZ5kwbdE6F3+w2RD1FN+U8IFiQAxBBWXHQXWFe0osHCNI455xz5LTlt99+6yVJ12Gx96RMYqqz68guAlJnLM7pppwHBAzFyyhWv7ONEgFizZo10odeUOXmD44RBfZYcEaA0T1Kti3WTR2oLbaY+NRNBhBCyB1ieKjJNkoECMr64osvSkFlh5xOUuMy6yYjngESNh+lSkp5EW9LuskAQgjpc4A/2LJly3TzN6PpJQMEmVOmaJ566ilteVXKhXaLImpHXqofYqExKCuLBhBCCOboAUS2DazdAALhbNasmSy/rh8CulR27VrAQZfJyQ6VV4DgpZWJgSDIACKPq4wjmjZtGgSPM5amW0DgJB2r2pUqVRJcp0q0BJjWV4NpjBcABp7bWw2v31Ljh6CmyQ0g8mqke/fuokSJEl7rJ9Th3QKCQtA60Erq+CmQjv3QtWagrLQHpcpuAJEn0pMmTdLabQgDUrwAgvwyjkCQ2Xrql5R5fc6KGFDHM9upwrg9szod1PiBPBhA5NUE2q4IQzaNI7wCAlYw4wQfmIHyQ8pGlD2uGrzbn3u9Rx8rqPEDeTGAsNQIftzo+2YL+QEEZa9bt650cMhahVeKZ7lc2bL1mp41PLazAGuQemcGEBaO464Khlvnzy2vI3fpFxCsXh933HFyP4XXQjO7ZDeNCT+xZZvqDBMq35UrV/aaJU/hDSAs7EKviV1Y3bp1szyN7qVfQFBi9Jz4OXTo0ME1A5hBIg4zSrS0HMze8czJ9qzrhIWQM1akwx74IMkAwsZd/mLFixcX27Zts72J3m0qgKC0aMQihMOHD3dVeAbPtA7WQ5fjxk6dOokCBQqIoGaXVAENIBQn8s5Lly6VQhBl48eqSKkCgnTYOwEo5s6dq5JN+3ndunVyt1/Lli0D/7YBhAOLcdeUDYNrHYCAPRg6Y3aHFf1MEOUAlK+++mrgnzeAcGAxq6BUQNQH17oAwT5sTL7UqVNHdp/wmZ0uS4B//fWXqFChQtqshhhAOABi586dciEp6lstdQECFqkVYn4U6sC1VdA0atQo+b3BgwcH/SmZvgFEHDarrZZBznnH+bS2xzoBQf9dAUGdg/bLh60sZqwwauzGL7cOxhlAJODiFVdcIapVqyZwmB5F0gkI+KCAYD3TmgZFvXr1kt/Eonm6yAAiAafpJ2PLKIitigk+q+2VTkAolQ4rGNiGGhQp80DpXhMygEhSo4MGDRIHH3xwJDcP6QSEspJuBQSqLkER/h9QRw9iV1yiPBtAJOJO3jus3jVq1MhFyHAF0QUINFf5KaAaTqvJ7Nu4ceNkdyYI4wxK8ziRU/qgOG0A4YKzNN8IBLpOUSJdgKBrVLp0aWG3Ho4ZGFoMnRMPjEkYRAep0ZqoDg0gEnHH8g7hQiiiZBRZByBwTILQW72bWtgizUni1+7zzz+3PvZ9TYtTpkwZsXHjRt9ppBLRAMID9xo0aCBXbVPdBunhkykFTRUQU6ZMSdotQnDxfIoH1FRJbVCaOnVqqkn5jm8A4YF1VD4DPeXl00PUjARNBRD472Z1mp9AMpozZ44EDr6y/ZLSrh05cqTfJLTEM4DwyEbGE4ceemgghnY9ZiVp8FQAwQwSWr9uLfsNHTpUgoIdc15p9erVSVsir2n6DW8A4YNzzz33nKzANm3a+Iidvih+AdGnTx9ZPq8LYhgSYLzhxbUAK9Cs9WRqEG2vDQMIO0dc3g8cOFBW/oABA1zGSH8wP4BQfq779u3rOcN79+6V/iewzO3WRRnGB+w2nDx/WGMEA4gUmNm1a1cJCjbBhJHiAQKbqE6O6hkjHXPMMSKVBTe6P4cddpioX79+Upbg944WJUyqMQYQSastcYCGDRvKSg3C8G7iLyd/Gw8Q7GhzGhswgD7iiCNS3pXGLBGC3rt377iZxOEJYTZs2BA3TCZeGEBo4LryC+1nQKnh83GTABAsKCKg7Hjj780WTKfVZUCCgDLVqoPQ/yK9CRMm7Jfc+vXrpdFj3i1fvny/d2G4MYDQVAtsmqGSe/bsqSnF1JMBELjnXbx4saBbN2LECIEGL/uTP/zww9gHlONJ3Q5IMCoGT1auXCm/NW3aNHmPpfW1a9fGvh+mCwMIjbWhFrLQ+dmxY4fGlP0l5dRlYhKAgTOGA9h0wzQyg+AgNFeZQWK3G90jrAECDvZQpGtvgx+uGUD44VqCODNnzpQVj8tYfEVnkuyAQHO0f//+sSy9//77cqGRbpXTIDsWMIULpcYNGM4///wUUkpPVAOIAPi8YMECUbRoUWk8OZODbTsg5s+fL6wapKi2I6hPPvlkAFwQsiVo3bq1/Ma1114byDd0J2oAoZujeemhJo2aBwKHZfEtW7YE9KX4ydoBYQ25cOFCmTfGE0EQ4wWs7FF+dr5FhQwgAqwppjZ79OghhYK+9OTJkwP8Wv6k4wECFWvyw4IYi2k6iWlUdJoAQtWqVeUMl870g07LACJoDgshVRkwIIyQ0IUI2vqcKlI8QLRq1UrmRfe0J9qqrDyjisHUbpgW3BRPkp0NIJJxSON7NDmZ0UFdGvMqQZMTINRWUM66iPWN5s2bS5AxVsj0ZEIq5TKASIV7PuJau1GsDGMULaj9FXZA0CLQStFC6CC8DrEaXaRIkUh2j5x4YADhxJU0PEMjlPUKBBTT8+xM020p0AqIPXv2yDEDY4ddu3b5LuHWrVvFmDFj5J4Q8l6xYsXIdo+cmGAA4cSVND6je3H77bfLrhQCVrt2bYEKiJOukddsWQHBbBLpM7vkh1D96Ny5syhWrJhMB18NGAP4559//CQX2jgGECGpGla2MWKAp04EFyU73OUOGTLEd8vRpUsXqbrB2IU0WXdwS9999510q4UqCouMxAcMTCGz2JatZAARwpqdN2+eNEPPABxB5KCfjjkcZm/cdK2UHpGKX7NmzYQlBQCsHdB1Y7pUxTvooIPkfmlUPdzucUj4oZC/NIAIeQWxwIdSHrZVy5UrFxNU1C0w2c/sDn9tuke0MKyMK0sZSqg5s8+Bbg9rIThCYVccxpxRXy9btmwsXaZMcQdAeij9ZYPjGC9VbADhhVshCMvCF+oXgIDxBjaMMAiMqgiarVYQxLvGeACuwxgQ0x1q3LixVPZDK1X3Ql0IWOYpCwYQntgV/sDMIOEWzA4GwEKXZ/fu3eEvRAZzaACRQeYH9Wm0WpletYLioYceCupzWZWuAURWVee+wqA2MXbsWDkIX7Ro0b4X5iohBwwgErLHvMw1DhhA5FqNm/Im5IABREL2RPMl/qJZr7Aeptvkri4NINzxKVKhMCjAgJpVb3VwX6VKlcAUCSPFoASZNYBIwJyovmLalX0JVmJ1++ijjxZt27a1PjbXNg4YQNgYkg23tApOgq/WJ7KhjEGVwQAiKM5mMF26R05G02gleOdGFyqD2c/opw0gMsp+/R/HH1w8oTeASM5vA4jkPIpUiIkTJ0pAOGVaDbaD2qHn9M2oPTOAiFqNJckvYwfGEE7EO/tg2ylcLj8zgMiy2se0DINnO7E2UbhwYcd39rC5fG8AkWW1z/iBbpOV6CKxBkHrYLpLVs7kvzaAyM+TyD5Rg2ZaA0WAAzCwBsGA21BiDhhAJOZPpN4qHw+0EuoACHShTMvgrioNINzxKRKhaBloJdRhbSkiUYAQZNIAIgSVYLIQHg4YQISnLkxOQsABA4gQVILJQng4YAARnrowOQkBB/4PghiAQFXGYKcAAAAASUVORK5CYII=[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAIwAAACECAYAAABCk8NTAAAOmUlEQVR4Ae2da8gVxR/HhQh6IaiJCJEoEiGC6atME/WVCJkm3qW8pFKaeU/NS4aKmvdbVBApmZogXupJ0dS8380L3rLEIKSbKIL4wtvEZ/7/3zn77DN7zp7zzJ5zdncGht0z89vZ+X3ns7Mzu3t26ygXnAIFKFCnAFtn6hRQDhgHQUEKOGAKkssZZ4C5ceOG8se9e/eqy5cvq6tXrxYdr1y5ovbs2VOjbPZVqnDgwAG1fPlytWLFikwcNWqUmjVrlpozZ46VOHv2bDV//vxM+exr5cqV6tGjR6VysyT7yQDzyy+/qPfff1+NGTMmEwcOHKjefvttNWLEiKIj2w8fPjxTJuWznyNHjpTEQXZy8OBB9eOPP1aLn3zyidq2bZu1uHnzZn1g4JfEo0ePJheYJ0+eKH988OCBIj58+LDoKGX4y+a3C/FTINPDxK/qrsblUMABY0l16UEtFVexxQQCw0BVIud/WRdh5Ld/6fV03759etzgt+F3OQM+mOoUlBZU18ePH6uNGzeqyZMnq06dOqlevXqpjz76SJ/a2WbQoEEKmyQFIzAIigDEOnXq6Ni5c2f9+/r161oE+S352JLGthIAzV+O2JVTSGYupnpJGn7UrVs347u/rvzevn276tatm3r++ef1DIwZ5fr16zU0M2fO1OAAkFcP0SXOSyMwOISjDHYFCET2Os86QJDPzAcRvfkiCmkIiB3LIDux9y6xZfZ27Ngx9c8//3izaqzTYNiHDdgy7aVe7733nt5W6sbyjz/+UEOHDlXNmjWr5hd5y5Yt09sBxF9//VVtl+R3795d5zO1TloIBAZHT58+rR1/+eWXq4kmIsydO1fnf/7555JUYwkwXbt21XYnT56skR+UAKB9+/ZVzzzzjHrhhRf09gKcaZtnn31WA27KM6VRL6b8AMOU2BS+/vprXXcgILCkV2EbpuWS7t92+vTp2ubUqVP+rNj/zgnM4sWLteOcl/2BBu3SpYvOzzUmQVQEfvrpp9X9+/f9xRh/sw1H9zvvvKNu376tr2Vs2bJFvfrqq7qr9zcU5b7xxhsFXfOgDE5B1O3ff//N1AOQiATGJ1wzkrBw4cKMHv46iA3Lb7/9VtWvX7+g+ni3r+T1QGAQrUePHlogLnD5w61bt3Qegt+7d8+fnfnNVVZsWrRokWmITGbACjC+9NJL6u7du9UsOEVyGpg6daruTWg0bCdOnJjziK9WyP9/sB0Qv/jii9V6CsoHFAINLwcLUDVp0kT7cvjwYVORmbRff/1Vvfbaa6H9zWwYg5VAYGgMjhIam/EDAtNgLIm7d+/Wea+88kpOYebNm6ft6P7DBsrnkr0pkAcgDRs2VG3btlWNGzdWHTt2VBcvXjSZB6ZxFRbf+vfvnwHmwoULqlWrVurvv/+usd3SpUu1fdDp2bvBpk2bFGOqJIZAYDj/Imi+OHbs2EBdgO7111/XZSBi2AAUuQCg9+Mo/uyzz9T333+fafCw5WO3aNEiXS/vzIhxUJs2bWqUhx8dOnTQ9rn8LWT/cbUNBIabdcAycuRILSCi0cOwpEHl/E+DBQVsmWVQjn82EbRNKdKpV8+ePXW9du3apa/JMONr3769njH56wCg4gfTaX8gnzJFG5akJTEYgcHZfv36aUG/+eabGn4DTKNGjRRHJOIEBbp2YPGPE4LsvenMiExxxowZgelhG0nqjw/e+r/77rtqw4YN3mrodWykp+Wg8QfqJPneZRJPS0ZgEEgGeKbHEBj0IQx3s3M10pdffqnthgwZ4tc4728ajsGnxO+++04ROcJl3bskPVddvDtkek/9AUS2YUnDewGSbQBMehj/QBwb8pkEMFukXGZ3f/75Z6ZsKScJSyMwPP+C4wxoTQIycyCfC1hBgQZgaoydzDqCbEudLgPY1atXh9o1GsgYhsGyKWAjujAzTGowAiNXMoMGeFw6B4Rc4xeOupYtW2q733//vWL0A+Q+ffroelVVVYWu17p16/Q2QRcPz58/r5577jltYzpthd5RhRtWA4YulcGfXJmlZ+A3IhM5J2PDuR9gmFr7ew/uNQHSggULtE27du0yNyAL0YJu3R+5RhIUe/fubewNZZ9Sf/xh7CX1xx9ukuYL3h6EOjCL46AgHV24ZsWUnIOEtKSGDDCcg+k5cFqmmrL87bfftCjkc81D0pcsWaKINIYEumXssBFbloMHDxaTUEsakbHSiRMn9C0KblPkilwG8NbDvxMa1VsnWadu165d85sbfwMCpxuu/wBc8+bNVYMGDfTtAsDjvpd3XGQsJOaJGWC8fiC8N3rzWEc48mXpz+e3Nz+XnWnbqNKoh8Rc/uXbP2UwqAVm6WXybZOUfCMwSXHO+WFfAQeMfU0TXaIDJtHNa985B4x9TRNdogMm0c1r3zkHjH1NE12iAybRzWvfOQeMfU0TXaIDJtHNa985B4x9TRNdogMm0c1r3zkHjH1NE11iYoHhz2lBf1BLdIvmcI6nJ/fv32+0OHv2rCLmC4kFhscPkvhX1XwNmiufB+Jat25tNCE96IE57waJBIbXpAFM0OOUXgHStM4zQEHPJaHXmjVr8sqRSGD4TzQCJPlRybwtazBAE9Nz2D/99JPWy/TAv7+YRALD/6H5h6ILWQUYnwCMaZwCRPXq1csa51hLJDD824FXeLiQVUAe7GfQ64/ySG3WOngtccDw+ORTTz2l1q5dG+x1CnMYu9DDBEVeQRsmJA6Y48ePa1EuXboUxv/U2ATNgu7cuaP12rp1aygtEgfMqlWr9JP8obxPkRE9iwkKGfACTpiQOGB4ESEvOnIhq4BAYZoFcSpq2rRp1jjPWuKA4UjilWEuZBUAiqBZENdm+BNe2JAoYHi9GcCY3pgVVpAk2gEEYJgCIJmuzZhsSUsUMLzrhTd63rx5M8jfVKZzBZfTkinQ+5hOVSZb0hIFTJCT5UjfsWOHfrEz/4xMUnDARNSa8kq0pN2eSB0w3JBk6h3mjQ21YamUwPCCAF5Sne/tnrXxR7ZNFTDcvvde6XzrrbdEB+vLUgEzbNiwaj7xTsIoQ2qA+fnnn6sJK+Dw8mqOTNuRe1nsg6PfdtlSnrz6XnyRZZSPdaQGmK+++soIjIicpOWnn34aWSeTGmDOnDljBIZvBtAL2I58UxIIGSvZLlvKkzvQftij/DxiaoDhkOM5Gb+448ePj+RoLNUYRl48KX7xmrcoQ6qAQUgee0BcXmn/8ccf6/UooCkVMPgkPQ1vRo86pA6Yc+fOaUi4sEbgSicA2YamlMDIzUW+KxV1SD0wUUHzww8/qDfffFO/Ay/qRnTARKiwv4eRXUlPM2HCBEmKzdIBE2FTBQHDLuMKjQOmTMCwW3n9e5x6GgdMGYGJIzQOmDID44WGr79VenDARNhCucYw/t3K6anSoXHA+FvO4u9CgGG3fL2E6zSVDI0DxiIg/qIKBSYO0Dhg/K1s8XcxwHihmTRpksXa2CnKAWNHR2MpxQJDYXJ6qjRoHDDGpraTWBtgqIF8ELSSoHHA2GHDWEptgalEaBwwxqa2k2gDGC80H3zwgZ2K1aIUB0wtxMu3qS1g2I+cnsoNjQMmX6vXIt8mMFSD/3Fznaac0DhgagFEvk1tA+OFZvLkyfl2H0m+AyYSWf9XaBTAULL0NOWAxgETQ2DKCY0DJqbAlAsaB0yMgaHq06ZN0wPhKVOmROhJtmgHTFYL62tRjWH8FS0lNA4Yv/oWf5cKGKpcKmgcMBYB8RdVSmBKBY0Dxt/KFn+XGhiq/uGHH+oxzdSpUy16ki3KAZPVwvpaOYDBiSihccBYxyRbYLmAiRIaB0y2fa2vlROYqKBxwFjHJFtguYGhJoxluGHJacpGcMDYUDGgjEoAhqrZhMYBE9DYNpIrBRib0DhgbJARUEYlAWMLGgdMQGPbSK40YPCJe06MabgyXExwwBSjWshtKhEYql4baBwwIRu/GLNKBaY20DhgiiEh5DaVDEyx0DhgQjZ+MWaVDgw+8ZgnY5qwHwpzwBRDQsht4gBModA4YEI2fjFmcQGmEGgcMMWQEHKbOAETFhoHTMjGL8YsbsB4oeGflqbggDGpYiktjsDgOv+sZCBsgsYBYwkOUzFxBSYXNA4YU0tbSisVMDt37lRDhgyx/up4U0/jgLEEh6mYUgET5ccpBBreiEVwwJha2lLaunXr9FiAD2tFGaIEhnrzBizGNEAjn/L74osvonRJl52qr5mMGzdOi4zQxEGDBkUmcNTAeKERf1jyJbgoQ2qACfpI6NKlSxUf1bQdR48eraE8dOiQ9bKlrqtXr652AAg47iOhFg4Z95FQCyIqpVLTwwR9JHTBggVq//791iPfj+aI37t3r/Wypb70jtKreJd8pjiqkBpgEFBOEyLugAEDotJVlWIMQ+WZuos/LEeMGBGZTxScKmBw+ODBg/qjmrt3745U2FIBgxP0YvQ2TK+jDqkDJmpBpfxSAiP7LMXSARORylVVVWrgwIHWr/RGVN3QxSYCGLpivkHtj6XookMrXWGGaMM3vNFs27Zt6saNG6FqmAhgxo4dq+rVq6c6depULW7dujWUCGkyApRmzZrpgXLr1q21XjJoDnOAJQIYHAcaF3IrsGbNGg1Kjx49avQoYQ+uRADDEYIYLgQrcOfOHVW/fn01ePDgYKMQObEHhm4UYM6ePRvC3fSaAAqnbcCpTYg9MMuWLdPA1EaENGwLLDZO27EHhiNHBm3eZRogCOuj9ML+QS2ThM6dO+sYFqbYA9O0aVN9XkYMbwwrZhrsTMBwapo1a5aOhfQ+sQYGp+lVwo7w0wCHyUcBJmicV4iGsQZGhAh70ckkZhrSRCfTgSV5YTWMNTB0qZySXMivADq1adOmxiwJDTklhQ2xBoZBGxehXMivAD0JYHAthkdVuSXAkqu+hWgYa2CYUiOEC+EUkIEugMjBhoZhT0fsJdbAhJPJWdlUwAFjU80UlOWASUEj23TRAWNTzRSU5YBJQSPbdPE/uaqOMAzfhawAAAAASUVORK5CYII=[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAP0AAACWCAYAAAAVBo5lAAAgAElEQVR4Ae2dBdRXRROHbVERCwMTW7ELRcFOTOQAdjcGio2BqNiBhXnsDhBFUOwusBEFu7AVA1F0v/Oszvvte9+98e8bM+fcc2t3dva3O5uzu9MYJUVAESgUAtMUKrYaWUVAETCq9JoJFIGCIaBKX7AE1+gqAqr0mgcUgYIhoEpfsATX6CoCiZX+lFNOMf/880/VEHv88cfNqaeeWjV+pTAiHrUKu1Z8S4mfulUEohBIpPTffvutmWaaaczff/8dxaukf/A6++yzzdSpU0vyVw3H7733nllkkUWqWoghF4XJhhtuaN58881qiKk8FIGaIJBI6QcOHGio6atJKMhRRx1lrrvuumqyjeVFuN27dzeDBg2KdVuOg5EjR5rtt9++6gVKObKoH0XAh0Cs0j/11FNmm222qUmNTI242mqrmT///NMnW02+XXHFFVVvtbiC/vXXX7ZQuf32293P+qwIpAaBUKWnRrz22mvNMsssY15//XVbc/Et7KK57rvC3Mt3FH/99dc3zz33XE1BITzis8IKK5gJEybUNCy6LJtuuql55plntMavKdLKvBwEQpWe/va0005rZpxxRtOqVSvTunVrM+ecc5q2bduaBRZYwCy88MKmffv2ZqmlljLLLbecmWuuuayb2Wef3bRp08bMMcccZumll7YKjVJHXV26dLHKuNNOO5UTh1g/77//vtljjz1sGBtvvLHZfPPNTdeuXc22225runXrZnr06GF23nln62afffYxBx54oOndu7c54ogjzDrrrGPWXXdd07lzZ3PSSSeZk08+OdHVr18/i9d+++0XK586UATqiUCo0o8bN85sueWWZvfddzePPfaYrbWefvpp88QTT5gXX3zRjBkzxrz11lsGd9ScH330kfn888/N119/bX744Qfz66+/2mY7tV7UNWXKFNOrVy87ZlCrQT1q+bPOOss261Ha008/3b6fd9555pxzzjGMWfCNkfeLL77YXH755ebqq682119/fZPyM/5w2223GZrtvuvuu+82Q4YMMQ888IB56KGHDH37lVZaydx7771a29czR2tYsQiEKj0+aa4fd9xxhlqL52oTSk7teeONN9ZFMVDIDh062O5KtePi8qPLMvPMM5uPP/7Y/azPikAqEIhUeiRE2eeff35b61VTYmrfYcOGmWOOOaYmBUqYrLfccovp1KmT+emnn8KcVPSdgoxuDdOCSopAGhGIVXqERlFQ/GrW9vDaYYcdDDYA9SbCPeCAA2oS7M0332zHBGrCXJkqAlVAIJHSUytjnMO9WsRoPTwbQdTCG2ywQVXjQzwoyODLbIeSIpBWBBJrXTUVXsCoVsuhHNkwA64FMeippAikGYHESh8WCRTujjvuiKw1cRN3hfEPfqegcE2C6UNX2gpBNvjCi8stjERuVw75JnfcyzP3elFYWK4sPFdLPngxc+HiExdX3CbFNY5XGv4LtkFM5XtSGSVdfNiUgu8nn3xi9S9puLirWOnFwm3SpEnecIncQQcdZJu9NH19F9NoTAMmiSxugkqPDUASvz4BP/30UztdiGXgvPPOa+Wbb775zD333GMVmdmFRx99tJnXPffc0xsPiRvz+/gpV6ZmgYW8wBvbghdeeKGFC5Ej7H744YeXJZ+kNVOycURmHjx4sOnYsaNNL2QBY8Y8yBOkeRDXOJ71+s8UNLYbQSJOYZjKd8a/yFPE0Uek20svvWSw31h++eWtrcuaa65p1ltvPTN27Fg7xoWZOGHFEbxWX311c+yxx8Y5bfa/IqX/4osvrMUeSsg8fRjdeeedZtSoUTbx5557bvtMgvONO4XCTDPNZA4++OBYRSGiQaUHcL6XQoDKvPuCCy5ojXWkBuM7F8Y4WCMS1nfffdeMNV2DRx55xP7DSOmiiy6y8SAuZOqePXvafwwWlipXs4BCXshQffv2NVtvvbU3c9HFqLZ8ksHA44033giR7N9xjWeffdZmRjLzTTfdZDMy/sF1jTXWsPYQPlx9TPFXCwx9YfGNsLCmvPTSS71OaNXeeuutNn2xY5E8TNpzbbbZZnYxl88/vFnDQtz33ntv617y28svv2zQDYzbVlllldg4kwewLYHXvvvu680H3ghUUtMT6KGHHmpXlRHwq6++GhaG/Y7i4G6XXXZpISD26lj3UdP+9ttvkXwADj6SEQANpQ8rWX3M8HvJJZdYPldddVUTL9ctJruEE5YAUfGBv9SK1V6STDx32203a98gGLhyy/Pw4cND8Q7KJ36i7hgsLbHEEpbngw8+6HWKbBg1gRs1OWkTpNGjR0fi6rrH3uGwww6zeezoo4+ONJ++//77rRK5/kt9BpctttjCyh6Vn2gFEkcK+yAxiMs/VluSr4XAghYilQRp4yNqf/zSEosjcGRGDffMRkXJG+RVdk1PibfWWmtZ81oCfvjhh4O8m70LUChTkABEalVfc9V1T8IQnmT4UpUecKS0paQMA2vixImRCRAVH+RFPkpuWhK///67G4WKnmmdJOnOXHbZZVZ+H94IQIZMKh+zHTTNBwwYYHleeeWVLeLg4kqhJOkTdIg7zLlp3YVhjx9ajqyTwAya9MJkmooBK0kfYT5dyZoK5KX1hGKGyU64yIxSkgexRg0SVqn8wxRdCj34bbXVVvY7hVMYoVP4xbozipCBbhMrRXFPqzRK5iCvspSeQLG/J+PTnCVgmjxh5ALlSxjMV+GBHf/PP/8cxsZ+J3K4lUiWqvSAjn+aZpIovgCRmdLal8nc+GDX7yPkk/5stQx1vvzyS1s4xs0QIB/jCsSzUvngtdhii9mMiHkxPLHQDBKGVvxjbcaHH34Y/N3sHVxvuOGGZt/cF8I85JBDzGmnndZUMPCNwmaWWWaxTWpJf/xRgC255JKR6eny9z1Tac0wwwxm8uTJvt9N3wiX1h+FuSuDOMCkGxxY04HMXFLJxLX64BeVZhIGy9EpBDFhxz1jAz5ZxH3wXpbSU8LstddeNiAGLgg4an26AIW7oKJRCNA3XXXVVa2FXlDA4LsAI5GEHwtiADeO8CP9bV/TLOifboOvkJL4tGvXrkV8hAduyBjEOU5JxU/UneXHdH+S8CJsWmHIx7OPkspHs57+J+5p1hMfanKXwF5wJV/EEUpP/zeMCIumbjCv4B5/tDpQIGpG3pGv1C6eGzYDaGD7zTffuJ+9z9KtY7m5m+d4piDDzJt/jKpDWH5SIIEbA3hRBI+48SkwgRfrYOSZgtaHVVhYJSs9CUKiPfnkk5an9I1JhDASoBhp7N+/vzn//PPNhRdeaBfz0NRj4UtSoQmfSHOH8EeN6iZAmBzMEOCXK4kZbhhPic+OO+4YGu5nn33WFBajuZUQNRm10NChQxOxITziWKl8YMyqRElrFAy+we4FmVlwpdUWR5J2Ye74z6xJGDFTxJgBg4I0+RnIiuMZxuuXX36xZtPjx48Pc9Lsu3TrCJ8FWuR7numKUHHRNHf78tLNSppHw/KcCEHBsuKKK9r4EmcKK7AvZU+KkpWeVWnuzjD33XefDZTpozCBWWmGYABExuGiOcW7lNouUBJB352IwksSGaWHR1jYLg9JAEZYxb/7P+mzxJnCKowkcyy00EKJCzQfL+Rk7GG77bZLLDMLmMAoSj4yJ26QLwwL/BOuYCtKz+pB+YbMzHzAiwyYNB19cXW/0ZWJIsLnQnZXlig/wX/4Jd9GdTVcP7iXbtM111xj8zGj91x9+vQxs802m92zQeThTqsIbM444wyXVVnPhL/ssss2dZ/gT96Hv298ISyQkpSeGo4pBfoSJC4Kh/ISaFRJxsgrblCEIDH9wz+aREQqjnCDe3GLDMFMGMaDNfX45R5Hwj/oDqAlPs8//3zwd9O7DPa4StP0M+EDYdENAdsweYKs8ENGJp6VyPf999/bgT43rdkUBL7BguKCCy6w35M0sYkHMsYR6YrbUq44nu5/+NKFOPfccxPJg1/80G0CA/AJklQqVGYiNy0R3IcNqLo88BNFJ5xwgh1sRPfkAnP4s4I0KSVWehKKZgwB+C5Ggn1C840+N34oNILEf5qL/H/77beDv1u8kxlwyx0i8mzi4Qvb9Yz8ovQsF44i3DJY41MaiQ+bi4gMQV7IhH8GneJmI4J+5R0ZyCiLLrpobNzED3fkIy2QLwyTJPKRcX3pzDfi5fKmu8Z3asEoIk60EuN2SaL5TmamG0neQdFoOtNfZgUjA4uMV8wzzzy2EmIZMxu+0BJJQshx5JFH2ilnnpMSg3zEk7T1+aPG5z9jOfwHI1H6ESNGRAaD7MTLxxePTF/CO+xiH4iklFjpGfXeaKONrJIRGbnoS4ggbkYQAURJAYrMFiS+UXPAI0kThTBwK2HBn1H/MLDc8KQkpg8YRWR4poB8PCU+UbWaFI5Mcfl4RIUt/+666y5rsBRWsIi74J2BPvCpRD4yGIpG2kg6c+edHZHg/+OPPzYFLc374OBWk4P/HhgULGXQ1Q1bnsFDnoP3YHi+d9KD9GUKDf+lkHRvsB3wkeQvsIc3YUnzHiOlKMIPrQ4fwYcCj1H7YJzFQIc4JaVESk+gNDF9TQiEIBO4iugGjh/++YDCL81X/sfNjwpPCY87RCaIKiHFH3cZcIpKcPgyuBhmbCTxCQOZHXOID0ZIIqMrwwcffBDaQhB37EhEnL766iv5lPjOtBbhh8lHjRMlH2lNoeXzT3xoeeCfgkEIazK+hU1j4Q6/jDJjVNJIYmo5Ss4w2cAFTIinbx6d+KEj/KcQFBIjLZQzjCioae2GFfBUAGwl56s0sfwjTF96hYUXq/REBoaMlPLsEkAgKIFyMQLKN4g77tlrjn9kJL7JxVQYBQH/KOXCIuyGxzM88SOy4A8rJwk36N59d+UhTsJD3EjmxQAmyI93wpL40JQTN9xfe+01uyEIshEvX3z4xn+usF11cMMefpj6wlcuZJVn9y6y8w2/Mpbgk49ujcgXjDt8+CZpHSY/I8fwcPnjT3ChiY8sLjElxsYlbLUW/Oe6c5/J4MhQyhXHmy3eUHh441aupNiKUtNNdf0wbS3/yOf8E+IZ3QEzphhdGXlmfUJYfuA/Y17MDNCKcP3Cn3exO2HaMvhfZAjeI5V+//33b+qTIBgGLW6EqJ1lDpL/WE9xJ6Fk7pR3LvpnKLdcLGqhWY+C+EqwoKDyTvjwEzkIC3PEpBHGvTS/kZdRVQyMaJrSAmB6KsiLd5Ff4iPx4LuYQ2IwgTGPyCYyy50Snb4pPNzaQP4TDk08DDuQB34s/Nh1113toBO2/FyYP2M9xsAOm5AQXhL5qC0Y2ffJR0FHf1nix/Sq647xEAZM6c/jRtJa3IArMzv8I5Mff/zxtuDCH+903YK4Srx9d/gQFvlk8cUXNyuvvLItOCgQmYok72HAAxZyydy4jx9hk58xWcUuhLEFsEU+wZUNUSk0Gag98cQTbfwxNJK0FmzkXe58pzBkGlrwcGWgC8wiGtyRrig66QyGhO0zZgJP1i4wIyDhslmtEC1GwpeuMW6o/MjbcRSp9GRSLvoycrkM5Zu4E7e4oZkr/7lTM7jvNPMAqJSMAF/8EEEBF3AY0CmFD24xNKFWIwOw0Idmn/B04yjPxC0YBzc+WN0lkYFRXxSekWMfURskuVjERBxE5ij5kBvDkyj5JEyUH/mwD3fdS1yDae26QRa6RRSkFFjEEVv8uPUUPhzgW+rl4+N+kzjG3ZllcgfeJO5hd1qtkg5ueO4z/8GVAUSUlW3i3PRz3coz4YlOuS0r/tMSlLRw82WcHPiNVHoJPE13IhVUegaX3MxXirzl+isljKBbapykhjZBv1l5bwSuWcGm0XJmTunpCgSVftZZZ40taRsNtIRPv5LuAC0UJUWgEQhkTulRlqDSsxY/SbOmEQC7YVL70feu9/l9rgz6rAhkTul9zXsMM7LSnKQvrqQINBKBzCk9YDH145IsCHG/6bMioAj4Ecik0vujol8VAUUgCQKq9ElQUjeKQI4QUKXPUWJqVBSBJAio0idBSd0oAjlCQJU+R4mpUVEEkiCgSp8EJXWjCOQIAVX6HCWmRkURSIKAKn0SlNSNIpAjBFTpc5SYGhVFIAkCqvRJUHLcsE0U23gHrQIdJ/roQYDtosGNi91n1YrSA1KdPqnSlwg0mZcFP9yVkiHAEVVgxj6J7sYTbCji7rWXjJu6qhQBVfoSECSDsn8eGZedV5SSISDHlrkKzvZiWngmw6/arlTpS0CULZpQeGp57krJEAAvNvoMEjV/3LbZQT/6XjkCqvQJMZQmKn152cE3odfCO6OApMB0SWp63wGhrjt9rj4CqvQJMaU5L7U7ik/TVCkZAmDFwZYM3jGIxxFQdJO0lk+GX7Vdac5NgKgouYzYB98TsCisE6nRZRCPO4UAo/hKjUFAlT4B7tTw1ExsdSUXGVcKgQQsCuuE5nuwVURBwGamOgPSmGyhSh+Du2RaFN+9yMiaaWPAM8b25aVb5LqWQVH3mz7XBwFV+hicGXUODkLhhYysSh8DnjF2bt7Xd5cCNJ6Duqg2Aqr0EYii1DRD3fllca6ZVpCIvtMiCo7Qy+wH8/dK9UdAlT4EczHECavN+e5rtoawK+RnGfDE8s4dC6EgRfGVGoOAKn0I7gw2odi+Wh4vZOiwAiGEZeE+C4bgxEXNDm5hmBYOoAZFWJW+QcBrsIpAoxBQpW8A8jRt836WXQNg1SATIlB4pR80aJA9Cppjln///feEsFXmjOYtRir0bbFUy2oBwMnEHBfN6PwzzzxTGSjqu24IFFrpt9hiC2s4wggzF+eB14tQfM40l7Bnn332TBUAV111VZPsEod77723XvBpOBUgEKr0AwcONHm+9t133xaZlsy78sorGwqDelybbLKJad26dZMcnMmHDDPMMINZaKGFzGqrrVYXOcqJqyu3KP2SSy7ZsDxTgQ4Uzmuo0pPx8nxNP/30TcommVbv/7Z4ysWBQqtReaZwmltBhEOVvgKemfD62WefeZW+nn1TMfF1lWyRRRaxfWSmu9JMO+20Uwv8Dj/88DSLrLL9h0BhlZ7477HHHk0Zd5ZZZrHPGJH8+uuvNc8grsJnRdFdUN5//31bq0uBteOOO5opU6a4TvQ5pQgUWunpg3bt2tW88847hnPvhw0bZhUfS7tJkybVLMlQeGz6GfVOe40eBsIpp5xisXrkkUfMl19+GeZMv6cQgcIq/WWXXWYz7aOPPtosWR588EH7vUuXLubnn39u9q8aL4zaZ1XRJf7EYbbZZjP77LOPfNJ7hhAorNIvvvjiZuutt/Ym1fDhw810001nOnfurCajHoROOukkWzC+/fbbnr/6Ke0IFFLpL7nkEptpH3/88dD0GTFihGGEf9111zU//PBDqLui/fj+++8N4x9MeSplE4FCKj396W233TY2xbA4m3HGGU2nTp3Md999F+u+CA5OPPFEW2COHTu2CNHNZRwLp/QXX3yxzbRJT1hhoGqmmWYya6+9tvn2229zmQmSRor4zzzzzGb//fdP6kXdpRCBwin9oosuWvJBFaNGjTKtWrUyHTt2NF9//XUKk7E+Ih1//PG2wBw3blx9AtRQaoJAoZRedmx5+umnSwbzscces33ZtdZay0ycOLFk/1n3QGFHi+fAAw/MelQKL3+hlH7hhRc23bp1KzvRGfibddZZzRprrFG4ueljjz3W1vIY5ShlG4HCKP0FF1xgM+2zzz5bdop9/vnndtSa0evVV1/dfPHFF2XzypJHWjbY1B988MFZEltlDUGgEEr/zz//mAUXXNB07949BIZ/P1955ZWGKSkfPffccwbbcroGTz31lGnTpo1h7zcKgrzTMcccYwvMCRMm5D2qhYhfIZT+vPPOs5kWxY0i5u/feuutZk7effddc+mllxpaCpxnJ8TCHDbBYDOMTz/9VD7n7o6JLYZKvXv3zl3cihqh3Cv91KlTzQILLGCV87TTTjOY2brK6yY8m0A8/PDD5pNPPrH3s88+25xxxhkmrLCgq8DJNyuttJL14/LKy3Pfvn1tgfnBBx/kJUqFj0fulZ5tsFgJ9sILL5gPP/zQ3HfffebMM8+0TXXu1OKDBw821PIHHXSQ2XTTTa2i33XXXYZaPo4oEOaee267C05YYRLHI63/6bqA3WGHHZZWEVWuMhDItdL/+eefZr755jM9e/ZsAc0ff/xhWFOPZdmbb75p7y+++KKhNVAqUaDMM888pkOHDrZgKdV/Wt0feeSRVunzVpilFe96yZVrpT/rrLNspn3ppZcS4fnXX3/ZjR4Z+CuVKDDmnXdes/zyy5s8DHgxTkEt7zuSqlRs1H26EMit0lOTt23b1rDDSyk0YMAAg99y6OWXX7Yti2WXXdaMHz++HBap8YOyo/SMbyjlC4HcKj39dTLtK6+8UtcUIzwGDpdZZhnz3nvv1TXsagX28ccfW+z69OlTLZbKJ0UI5FLp2b+ewbVddtmlIVCPHj3atGvXziy99NImi3bqDNxRYDLmoZQ/BHKp9KeffrrNtChfo2jMmDF2G2u25MrSMlRmOFD4o446qlHQabg1RiB3Ss+mlsyd77bbbjWGLp7966+/brD3X2KJJew+fPE+Gu8CIxy2si6KiXHjEa+/BLlTeqbcqKnSsg/dG2+8YVjO2759+xbWfvVP7ugQmXUAu6OPPjraof7NNAK5UvpffvnF2sSztXWaCNNeduvhwiYgrcSCGrYI++qrr9IqospVBQRypfT9+/e3NRW1a9qITSSp7dnjPo3ysWSWWp4ltEr5RiA3Ss921XIIZFqTjP316d/Tz09L90OwwgSZ/QCLvDOQYJH3e26UXg5fSHPzmcyEPT8j+iz1ZYQ/DYQ9AbU822Ep5R+BXCh91g5fYO6eOXzm8l999dWG57IDDjjAbnj5zTffNFwWFaD2CORC6bN4+AJ9aKz25p9//rpbDbrZipYHtTxbWysVA4HMK32WD1/APn+55Zaz9vpJFwVVO1vut99+dsNP3de/2siml1/mlT7rhy+wOQUr81gcxEq9ehIDi9Ty/fr1q2ewGlaDEci00ufl8AVMX1dYYQW7Jv/5558vO0swmFkKcQAlB1HqsV2loJZ9t5lW+jwdvsDKthVXXNEuFArbnisuu7EcdvLkyXHO7H8MhqjlTz755ETu1VF+EMis0jOfzLxyng5fYO06++2xdoCNN0slNg1hFx+m4DAGYpaALa/YQShIe+21l2ndurX56aefgr/0PecIZFbp83r4AstZ2WGXnXaTnMSDvTz7/qHwm222md2Xn/P6Lr/8cjNo0CC73x9LZQcOHGjd0ZXAIpBa/tRTT8159tbo+RDIpNJjG46NeF4PX6B2Zk99LAzDDtpklx42/WS33uHDh9u9+Th664477vCls/3PTsAsSFpzzTXtGoVJkyZ53erHfCOQSaVnFRg1VR72ogvLXuw3zyk6NMGfeOKJJmcUCOzce+GFF7ZYvENznu9RhPkv2JWzAWgUX/2XHQQyp/Ss82a9dxEOX6BFw7l5nJ/HOXr014m3Wwi4WY2am2Z9FO2+++52zIB9B5SKiUDmlJ4dXaipinL4AufIcVIu58KjsPTJyyV2EgI7dhZSKi4CmVL6oh6+gE18x44d7VHRo0aNKju37rrrrnZK8Lfffiubh3rMPgKZUvoiH76AIdI666xjFZ+jt0oldumllmeXYKViI5AZpZfDFzg5tqjEOoNOnTrZY6NHjhxZEgw777yzNfVNarxTEnN1nCkEMqP0evjCv/kKk9n11lvPTlk+9NBDiTIb03vU8szVKykCmVB6PXyheUbFiq5z5852FoM5+jjq1auXXck3ZcqUOKf6vwAIZELp9fCFljmR7cG6dOlia/AHHnigpYP/vrByj1qeY7eVFAEQSL3S6+EL4RmV3X832GADq9TDhg3zOuzRo4fdqIPDOZUUARBIvdLn5fCFWh33jJHNhhtuaBV/6NChzXI1y3Sp5c8999xm3/Wl2AikVunZyYUlpmTarB6+gKKz+AU7+uuvv75mOY2z+zbeeGOL1ZAhQ2w4bMfVvXt3uw/f33//XbOwlXH2EEil0nPwJMrOhcltWnaNTZK8ougskZU41FLhRSam4jbZZBMbJgt1JOyePXuKE70rAhaB1Cm9bIwhmZZ7t27dUp1cPkUX+euh8AIOZ+dJuO49zwuTJO56T45AqNK3atXKNOKiZnczrD7/2+KpBAc2G2lEWtYzzORZXl2GKv2AAQNMIy62hQ5mcDIPfdY0XjTj2b+e9f3I7RZaLItdf/316ya326VwMeQE30akZT3DVFVOjkCo0idnUV2XTD25GZbniy66qLqB1Igbg2h77rmnXQMvcUAROYyjXrT22ms3w49CR0kRcBFIndIjHPvDHXrooXbrp+A0lCt8mp+lAGjTpo0dva+X4jOgx9ZZzM+zs87UqVPTDJPK1gAEUqn0DcChpkFSAGSltVJTIJR5KhBQpU9FMqgQikD9EEid0jP9xTnzctG855tS6QiwrRb4caXtaOzSY6M+qoVA6pSebZnZ/hmbcrErZ1CsT58+1Ypz7vnQnWjfvr0d0FtsscUsnmDI8mQlRSB1Sr/99ttbZXeThoKATFtPQxc3/Cw9gxFYgZk7eEhryX3PUpxU1uoikDqlp2byHcJArY8Nu1I4ArK9tQ4ahmOkf1K2yo7aiFrKt8Wz1PaaaOEISJco3IX+UQRSpvT0RVF6XzNUlT46u0qBqV2gaJz0b8qUHsWmee8jVXofKv//Jn15X4H5f1f6pAikTOlpnmLG6iMOdeRS8iOghaIfF/3aEoFUDeTRtPcNQskAlTZdWyagfFGlFyT0HodAapReFDs4iEdzlVF7anltuoYnpzTv1ZApHCP98y8CqVF6ybRuwvANhaefrxZlLjItnykQMWraYYcdWv7UL4qAg0BqlJ6+/Jxzzmk3eRRrMjIx37WGd1Is4lEKTm7n1EYAAADASURBVPDDghFTZjbN9HWZItjor5wjkBqlpyanae9eOce+JtEDR/r3YtnIszb5awJ1ZpmmRukzi6AKrghkDAFV+owlmIqrCFSKgCp9pQiqf0UgYwio0mcswVRcRaBSBFTpK0VQ/SsCGUNAlT5jCabiKgKVIqBKXymC6l8RyBgCqvQZSzAVVxGoFAFV+koRVP+KQMYQUKXPWIKpuIpApQio0leKoPpXBDKGgCp9xhJMxVUEKkVAlb5SBNW/IpAxBP4HC3k/7SZWH6IAAAAASUVORK5CYII=[/img]
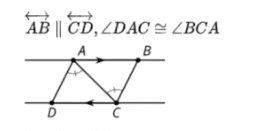
[size=150]Andre remembers lots of ways to prove triangles congruent. He asks Clare, “Can we use Angle-Side-Angle to prove triangles are similar?”[br][br]Clare: “Sure, but we don’t need the Side part because Angle-Angle is enough to prove triangles are similar.”[br][br]Andre: “Hmm, what about Side-Angle-Side or Side-Side-Side? What if we don’t know 2 angles?”[br][br]Clare: “Oh! I don’t know. Let’s draw a picture and see if we can prove it.”[br][br]Andre: “Uh-oh. If ‘side’ means corresponding sides with the same length, then we’ll only get congruent triangles.”[/size][br][br]What could ‘side’ stand for to prove triangles similar?
Draw a diagram that would help you prove the Side-Angle-Side Triangle Similarity Theorem.
Write a proof.
Prove that these 2 triangles in the applet below must be similar.
Prove or disprove the Side-Side-Angle Triangle Similarity Theorem.
IM Geo.3.10 Practice: Other Conditions for Triangle Similarity
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUIAAAEaCAYAAABkcF4GAAAgAElEQVR4Ae2dB7QURdqGBUFAkigS9CeKgkgSl6AEEZCoK0kBAQkCS5IgQXIOgihIVFSii6AoyQhrAEEREAXJIBkVVCQjIH7/eWtP3507d2buhA7V3W+dM2dmerorPNX9zlfpq+uEgQRIgAR8TuA6n5efxScBEiABoRDyJiABEvA9AQqh728BAiABEqAQ8h4gARLwPQEKoe9vAQIgARKgEPIeIAES8D0BCqHvbwECIAESoBDyHiABEvA9AQqh728BAiABEqAQ8h4gARLwPQEKoe9vAQIgARKgEPIeIAES8D0BCqHvbwECIAESoBDyHiABEvA9AQqh728BAiABEqAQ8h4gARLwPQEKoe9vAfcC+O677+SLL74QvDOQQCIEKISJ0HPo2jlz5ki1atVSvPwiCMOGDZObbrpJrrvuuqRX6dKlHaoNJusFAhTCMLWIh2348OHqtWzZMq2sjscee0wefPBBQR4DXwcPHgxTGu8cbt26tWTPnl3wZ2CEP/74Qz7//HPjK99JIGYCFMIQyPBgwdqAlQHBwQvfGzRoEOJs+w8ZImh/ys6mCNGHCPrF8nWWtr9SpxCGqG9YFxA+CKIR8PDhmA6WB4Rw0qRJRtZ88Y66QHMYYshAAmYToBCGIIqHLVSfE4QwsEkW4lJbDsEqWrp0qa8GCsA9+M/JFthMxBcEKIQhqhkWF/qiAgMsMAiQDv1wyAdEwXjH5549ewZm13OfjX5RzxWMBdKCAIUwRDVAYDAqawyWlClTRlmIOjSLQ2RXNdeRZy83G/HnBDFkIAErCFAIg6jC4oOF1aNHDyUsePgKFCigvcWF/EKwvRoohF6tWT3KRSEMqgejLyrwMDrqYXHpPEABaxCC7dWAroqCBQt6tXgsl8MEKIRBFQDLCtZHcNDdIoHl6uWmozGSH9wXGjiyH1xn/E4C0RKgEAaRguBBDAODTlM3IAht2rSRuXPnqlFjTPZGfyYsVh0GcgK5mf0Z1jrKiWk0KDO6AtCNwUACiRLgXRREEA8WBkmwhhUvCA0eODQ7dbA+kAfDaoVo44Vmow55C0JpyVeIPaYOoSsA714Xf0sgMtIUBCiEAUiMSdMQQ+OF+YR46PwiNAE4+JEEfEOAQuibqmZBSYAEwhGgEIYjw+O2ETh+/LgMHTpU9X3OmzfPtnSZEAkYBHwnhFeuXJEff/zRKD/fHSaALgdMizG6IvDeu3dvh3PF5P1GwFdCOGrUKMmQIYN66EqWLClffvml3+o7ZHmvXbsm+IO4ePGinD17Vk6dOiW//vqr/Pzzz3L06FE1ILF//37ZvXu3bN++Xb7//nv59ttv5ZtvvpH169fLmjVr5LPPPpNVq1bJhx9+KCtWrFADGe+884689dZbsmDBArVG+/XXX5dXXnlFpk2bJpMnT5YXX3xRTfkJFEF8TpMmjVy6dClkXnmQBKwg4BshNOahBT5099xzj5w7d04NhODB/+WXX+TYsWNy6NAhMR78HTt2yNatW5Me/K+++krWrl2b9OB/9NFHsnLlyqQHf9GiRfLmm2+q6S148F999VWZPn26vPzyy+rBnzBhgowdO1ZGjhypmoODBg2S5557TllBGA3u2rWrdOrUSdq3b6+aii1btpTmzZvL448/Lg0bNpRHH31U6tWrJ7Vq1ZLq1atL1apVpVKlSlKhQgW577771FLAEiVKSLFixaRIkSLK2sqXL5/kzZtXbr31VsmRI4dky5ZNbrzxRrnhhhskbdq0yayxQD6xfL7++uvVn0zmzJlV/DfffLPkypVLbrvtNsmfP78ULlxYihYtKmCOASjktWLFimo0PlQ6J06csOJ+Z5wkEJKAb4QQwhPqgYv3GKyWdOnSScaMGSVLlixqbtstt9wiuXPnlttvv1094Hj477rrLilevLiUKlVKypYtK+XKlZP7779fqlSpIg899JDUrFlT6tSpI4888ojyd9i4cWNp2rSptGjRQk2LadeunXTs2FG6dOki3bt3l169eknfvn1lwIABMmTIEBkxYoSMGTNGxo8fr4R2ypQpMmPGDJk1a5aywmCNwSqDdYapQO+//758/PHH8umnnypLDhYdLLstW7bItm3bZOfOnbJv3z5lBcIahFX422+/yenTp+X8+fNy+fJlgQWZSLh69aq89NJLUqhQoZB1Urt27USi57UkEDMB3wghrLRg0UMz+euvv1bWHqw+NPvQ/IM1CKvQKiGIuZY8csHJkyeVeMMqRV20bdtWsZ4/f76yErNmzar+BCC+DCRgJwHfCCGgGg+gIYiwohisJ7Bnzx555plnkv6IMBiCfkgGEtCFgG+EEM1HCCCaky+88IKyBHWpBK/mY8OGDYI+TnBH3yHqgIEEdCTgCyFEHxgeRgxKMFhPAH2Q9evXV8zRX4o+SwYS0JmAL4SwfPnyaqBC54rwQt4wKPPAAw8oAcT0JIygM5CAGwh4XggHDhyoHsx169a5oT5cmUdYfHfffbfiDCcQmE/IQAJuIuBpIcQkXzSJvezC3qmbDZOv0eeH+YlgjDmOmzdvdio7TJcEEiLgaSHE5F001RjMI3DkyBE1jxHzJyGAmOfIJYvm8WVMzhDwrBBilQYeVCwFY0icAJbVYbULmGIieZ8+feiaLHGsjEETAp4UQix5wwP7/PPPa4LZvdmAc1qsdgFPLJvD8kAGEvAaAc8JIRbrw5t0jRo1vFZXtpYH3p+xlhkCCO8wcJbAQAJeJeA5IXz66afV4n+smWWIncDs2bPl3nvvVQII5wiLFy+OPRJeQQIuI+ApIcQ8NlgwcPHEEBsBuMQynCBgY6TVq1fHFgHPJgEXE/CMEMJDSs6cOdWKBhfXh61Zh+9BLDnErnD4A2nUqBEHl2ytASamCwHPCGGzZs3UA33gwAFd2GqbDzDq1q2bEj8IIEaDuRucttXFjNlAwHYhhGt2jESauSscHKDigYYTVIbwBLDmGn4OwQpOEPr16ydnzpwJfwF/IQGfELBdCB977DH1IMJjtBnh8OHDkilTJmnSpIkZ0XkyDnjRhldrCCBWgowbN86T5WShSCBeArYK4Zw5c9SG5HggzRJCuK7Hw01nnilvgYULFypv2OAN1/20mFMy4hESAAHbhBB9UOiUNzZRN0MIsQ8IHnJuAZn8ZsYeKYYTBHjegZt+BhIggfAEbBNCeCUxnB+YYRFiUyXEA8efDP8lMHr0aMmTJ4/igr1QsC8JAwmQQOoEbBFCCCCE0AhmCCE2PsLmSGYOuhj5c9M7yo91v8Y2pVgOh42YGEiABKInYLkQoimcPXv2ZNMzEhVCw+3+22+/HX1JPXbm3r17BatowBJOEDp06KA2nPJYMVkcErCFgKVCCGsF61QxSBIYEhHCjRs3qocfD74fA/ZVxsRnMIQTBGw/gInRDCRAAvETsFQIJ02apAZIhg8fLoEvPMRt2rRRx2LNOjr/sYH5n3/+Geulrj5/+fLlah9ksMOfC3fgc3V1MvOaEbBUCDEyjP7B4Bce5tatWycNnkTLxHC7DzdbfglvvPFGMicI2LidgQRIwFwClgphuKxCCGOdPoPzcR32x/VDmDhxorL8UOYqVarIkiVL/FBslpEEHCHgGiGE2/1y5co5AsnORAcPHqwGlyCA2BIT+64wkAAJWEvAESGEdRfLtBfD7b5XXUP9+uuv0rVrV2XxQgCffPJJgWt8BhIgAXsIOCKEsRTNcLsPBwFeC3AeC9GD+MEJQqdOnQRrpxlIgATsJaC1EF6+fFm53a9ataq9VCxObe3atVK3bl0lgFgn3b9/fzl37pzFqTJ6EiCBcAS0FkLD7b5XNmd/9913kzlBmDBhQrh64XESIAEbCWgrhIsWLVIW09ChQ23EYU1S8PoC7y9oAmMeJPwnMpAACehDQEshPHXqlHK7X7t2bX1IxZETLAXMnTu3EkA4QYBFyEACJKAfAS2F0HC7v3nzZv2IpZKjq1evSu/eveWGG25QAggnCLHOmUwlCf5MAiRgMgHthBArKdCEdNvm7HAM265dO5V3OEFo27atbN261eTqYnQkQAJWENBKCI8cOaLc7jdo0MCKsloS5w8//CANGzZUAggnCJjzePToUUvSYqQkQALWENBKCA23+3C6qnvAig/4RIT1CicIGNS5cOGC7tlm/kiABEIQ0EYIDbf7eNc5wAdimTJllACWLl1asCaYgQRIwN0EtBDCXbt2KWHBKgtdA/YBKVCggMonnCCgLzO1gGWE2Lp08uTJ6j218/k7CZCAMwS0EELD7f6PP/7oDIUIqY4YMUKyZcumBBBOEJYuXRrh7P/9hPOwWRWsRmxTABGFJRnLGuv/xcZPJEACVhJwXAjHjh2rREYnP3tw+tqtWzeVL/QBwlJds2ZNTPWA7QngmDYwQAwxmMJAAiSgFwFHhRDzBCE0WEqnQ8Bob/PmzVWeDCcI27ZtiytrKFfw/EGIIDa4ZyABEtCLgKNCaLjd/+mnnxylgg2mAp0gYB+QY8eOJZQnNIcDpwEZ+zoH79+SUCK8mARIwBQCjgnhoEGDlOW1YMECUwoSTySrVq2SihUrqnxgLTCWxF28eDGeqFJcg75A9A9iak3Pnj1VH2FwUznFRTxAAiTgCAFHhBAjqWg6oh/OibBw4UIpWrSoygOs0qlTp5qeDQghBBB9hegbhCBGO9BiemYYIQmQQEQCjgih4XYfzhXsDFOmTJFcuXIpAYQThPnz51uWPKxB9Acao8RoEocaQLEsA4yYBEggagK2C6Hhdt/OzYiGDBki6dOnVwIIJwjLli2LGlA8J8Lyg8VriKARB8QQU2oYSIAE9CJgqxB+8MEHSiD69u1rOYXz589L586dVXqGEwR4hrYjQPDQFA4Oxk58wcf5nQRIwFkCtgkh3FOhrwxu9y9dumRZqQ8dOiRNmjRRAmg4Qdi+fbtl6YWKGCPEsAgDR4hhHWIUGaPJDCRAAnoRsE0I27dvLxkyZBBYhVaETZs2SbVq1ZQAGU4Qjh8/bkVSUcVp9AkiL0a+IIIQSQYSIAG9CNgihHBUAAvJCrf7H330kZqmgvgNJwhWWpyxVh/mKKJJTAGMlRzPJwH7CFguhGgS5syZU8x2u48R3/z58yuBhRMEnZbo2Vd9TIkESMAMApYLIZasYaQ0eLlZvJl/6aWXJGvWrEoA4QRh8eLF8UbF60iABEhAEbBUCGfPnq0Eywy3+wMGDFBxoQkMJwhoEjOQAAmQgBkELBNCrNXNlClTsvW2sWb49OnT0qFDByWAhhOEr776KtZoeD4JkAAJRCRgmRAabvc3bNgQMQOhfty/f78SUFh/efPmFThBcIP7/lBl4TESIAH9CVgihFi7CxGL1e3+119/LZUrV1bXGk4QsDscAwmQAAlYScB0IdyzZ48Ssljc7q9cuVIgfBBPwwnC5cuXrSw34yYBEiCBJAKmC2H16tWlcOHCUe3pi8GUW2+9VQmg1U4QkkrMDyRAAiQQRMBUIcToMKy61Ob0TZgwwVYnCEFl5lcSIAESSEbANCH89ttvlQhGcrvfr18/dY7hBAF7AzOQAAmQgNMEQgohVoNgfeywYcOizl+FChWkRIkSsnfv3mTX/Pbbb9K2bVslgIYTBIgmAwmQAAnoQiCkEEIA0cSN1lPK4MGD1fmBbvd3794tmEKDeAwnCPv27dOl3MwHCZAACSQRSCGExiZDEMNQPvWSrhQRjOzCxx/EznC7v27duqR9QAwnCCdOnAi8jJ9JgARIQCsCKYSwdevWyhKM5EQU63tLliypBBArPooXL6724yhSpIg6ZjhBuHLlilaFZWZIgARIIBSBZEIIl1Gw7vBufA52H3XgwAF1Ds4zXmnTplWf6QQhFGIeIwES0J1AMiFEnyAsQiNA6IK9xrz22mtJAmgIId6nTZtmXMZ3EiABEnAVgSQhNJrCc+fOFWy3aWy5GehuHiXDxkeBAmh8Pnz4sKsKzsySAAmQgEEgSQgxsGGIWuB7qCk0xnpg4zx4iGEgARIgAbcSUEJo7K8RvP0kmsrYmzc4/P3338qhQqdOnSzdGzg4XX4nARIgASsIXAfxwzSZUJYfjkU7l9CKzDFOEiABErCDwHUQu+zZs6fYjByJ4zduSG5HNTANEiABJwlcN2nSJDUHMFQmMHUmlKUY6lweIwESIAG3EkgaLHFrAZhvEiABEkiUAIUwUYK8ngRIwPUEKISur0IWgARIIFECFMJECfJ6EiAB1xOgELq+ClkAEiCBRAlQCBMlyOtJgARcT4BC6PoqZAFIgAQSJUAhTJQgrycBEtCWwNKlS9W2I9h6JPAV7FWLQqhtFTJjJEACiRLo0aOHwKEMhC/wFexXgUKYKGleTwIkoC0B+EqIZnUchVDbKmTGSIAEEiUAV4FoHqcWKISpEeLvJEACriRgOJsO3m4kVGEohKGo8BgJkIDrCcChDCzC4cOHJ3uFKhiFMBQVHiMBEnA9Aey/VKBAAeVTFX2FeAXuyRRYQAphIA1+JgES8AwBiGA0AyUoMIXQM9XOgpAACRgEMD0GzeLg+YLG78HvFMJgIvxOAiTgegLGQEnwfMFwBaMQhiPD4yRAAq4lgCYxmsbRBgphtKR4HgmQgGsIYO5g8J7skTJPIYxEh7+RAAn4ggCF0BfVzEKSAAlEIkAhjESHv5EACWhJYO3atdKvXz8ZOXKk7N+/P+E8UggTRsgISIAE7CQwb948NTUG02PwypIli2zdujWhLFAIE8LHi0mABOwmcN999yUTQohh165dE8oGhTAhfLyYBEjATgJXr16VbNmypRDCxo0bJ5QNCmFC+HgxCZCAXQRWrlwpDRs2TCGCsAhff/31hLJBIUwIHy8mARKwmsC3336rmr6ZMmVS7vbRNE6TJo2kTZtWbrnlFhk8eHDCWaAQJoyQEZAACVhB4Oeff5YxY8bIHXfcIYUKFZJXXnlFevXqpSxCuNYyM1AIzaTJuEiABEwhMHv2bKlSpYqy/AYMGCCnT59WnqbRDG7UqJH89ddfpqRjREIhNEjwnQRIwHECH3/8sTzxxBPK6nvyySeTpsX89ttvapCkSJEismXLFtPzSSE0HSkjJAESiJXAtm3bpGfPnkrsKlWqJCtWrEgWRf369ZU4zp07N9lxs75QCM0iyXhIgARiJgBLb8KECVKsWDH5v//7P5k6dWqKOMaPH69E8Nlnn03xm1kHKIRmkWQ8JEACMRF48803pXr16krk+vTpIydPnkxx/VdffaV+r1mzppw6dSrF72YdoBCaRZLxkAAJREXg008/lZYtWyqBe/zxx2XTpk1hr7vzzjslV65c8sUXX4Q9x4wfKIRmUGQcJEACqRLYtWuX9O3bV839K1++vCxZsiTiNU8//bQSyylTpkQ8z4wfKYRmUGQcJEACYQmcOXNGsLVmyZIlJXfu3PLiiy+GPdf4AYMimCrTvn1745Cl7xRCS/EychLwN4HFixdL7dq1lah1795djh8/niqQH3/8Uc0fhNV46NChVM834wQKoRkUGQcJkEAyAl9++aW0bdtWCeBjjz0mGPSINmAidbp06VJMoYn2+njOoxDGQ43XkAAJhCQAJ6mDBg2SPHnySJkyZeStt94KeV64gwMHDlTiOXr06HCnWHKcQmgJVkZKAv4icPHiRZk2bZqULVtWTYp+/vnn5e+//44JAlaVoF8QK0vsDhRCu4kzPRLwGIH33ntPHnnkESVinTt3jqtf78KFC2ogBROrscrE7kAhtJs40yMBjxDYsGGDdOzYUQ1s1KtXT9asWRN3yZo0aaKEFJOsnQgUQieoM00ScDGBI0eOCNxg5cuXT+655x6ZP39+QqXBPEE0ibEZk1OBQugUeaZLAi4jADf5r776qlSsWFFuuOEGGTVqlFy+fDmhUnz33XdKBOvUqSNnz55NKK5ELqYQJkKP15KATwgEusnHJOe9e/eaUvJSpUqpvsF169aZEl+8kVAI4yXH60jABwQMN/mwAB9++GFZvXq1aaXu1q2bsgZnzJhhWpzxRkQhjJccryMBDxMw3OQXLlxY4Aw10c2RglFhxQn6BTt16hT8kyPfKYSOYGeiJKAvgTlz5ig3+RCqIUOGyPnz503N7E8//SSZM2eWBx54QI4dO2Zq3PFGRiGMlxyvIwGPEcCE5qZNmypL7amnnpIdO3ZYUsJatWqpJXQffvihJfHHEymFMB5qvIYEPETAcJMPK+3BBx8UKwUKI82wNLHyRKdAIdSpNpgXErCRgOEmv2jRonL77bfLzJkzLU0dzlUhgtiUSbdAIdStRpgfErCBQKCb/P79+1vqBh/Fwbpj7E189913y86dO20oYWxJUAhj48WzScDVBD777LMkN/nNmzeX77//3pbytGrVSlmDixYtsiW9WBOhEMZKjOeTgAsJwE0+lrBlz55d7r//flm+fLltpZg1a5YSQbjY0jVQCHWtGeaLBEwgYLjJL1GihNorxI79PwKzvXv3biWC8E4DV126BgqhrjXDfJFAggQC3eT37t1bTpw4kWCMsV+OdcnYhQ6eanQOFEKda4d5I4E4CAS6yYd7q40bN8YRS+KXYMc6jBKjaax7oBDqXkPMHwlESQCbHsFNfs6cOeXee++Vd955J8orzT9txYoVSgSxntgNgULohlpiHkkgAgHDTT72CMGk6IkTJ0Y42/qf/vjjDyXGlStXll9++cX6BE1IgUJoAkRGQQJOEQh0k//MM89osXYXu9Zdf/31smrVKqewxJwuhTBmZLyABJwnYLjJRx/cP//5T1m/fr3zmRJR1ijy5LRVGisMCmGsxHg+CThIwHCTnzdvXrVKY+HChQ7mJnnS33zzjeoXhMMGtwUKodtqjPn1JYG//vpLjb6WK1dO0qZNK+PGjZNr165pxQL7l2AJnVneq+0sHIXQTtpMiwTiIBDoJh+OTA8ePBhHLNZegt3s0CResmSJtQlZFDuF0CKwjJYEEiVguMmHBQgffvDeomNYsGCBEsGhQ4fqmL2o8kQhjAoTTyIB+wgYbvLz588vBQsWlHnz5tmXeIwpHT58WDJmzCgYKb5y5UqMV+tzOoVQn7pgTkhA4CYfLuzRzBw5cqT8+eefWlOpXr26WkK3efNmrfOZWuYohKkR4u/aE8AE3kjNRuydO3fuXPXCZx3DJ598Ik888YQSwKefflr27NmjYzaT5Qn7mUCwZ8+eney4G79QCN1Ya8xzEgEIG5qPeCCDAwYVqlWrplxPwQU9XjivZ8+ewac69h1u8nv16iUZMmSQqlWrumYSMrb11I1lIpWY8u5JJDZeSwI2Epg0aZJ6GFu3bh1SCGEpDhs2TPBuhM8//1yd67RlaLjJv+OOOyRPnjzy2muvGVnU/h3NdfRfYgkdyuGFQCH0Qi36tAwQQAiaIW7RYoAlAxF1KsBNvmGdDh48WM6dO+dUVuJKt1mzZmoJHbxdeyVQCL1Skz4uRzxCiGvsDhCOFi1aKIu0ZcuWsn37druzkHB606dPV/mfPHlywnHpFAGFUKfaYF7iIhCLEMISLFCgQFzpxHsRvDTDTX6WLFmkfPny8sEHH8QblaPXoT8T1nTbtm0dzYcViVMIraDKOG0lEK0QohmNB9kua9Bwk1+sWDG56aabZMaMGbZyMTsxLO/DEroDBw6YHbXj8VEIHa8CZiBRAtEIIUQQYoR5enYEuMmvWbOmEt7nnntOfv/9dzuStSyNHj16qLIsXbrUsjScjJhC6CR9pm0KgdSE0E4RhJv8Nm3aKNGAm3yk7faA9cOwpEeMGOH2ooTNP4UwLBr+4BYCkYTQLhE03OTnyJFDSpYsKcuWLXMLvoj5PHnypNx8883K56Fu3m4iZjzGHymEMQLj6foRCCeEdojgpUuXBCOpED9Min755Zf1A5RAjurXr6+W0HnBso2EgUIYiQ5/cwWBcEKIydRo0oV7JVo4uMmvW7euih+rQ9yyP0e05R47dqwqm85OH6ItS2rnUQhTI8TfSSCIANzkd+jQQYkELCZ4ZvZaWLdunSof9kP2Q6AQ+qGWWUZTCBhu8m+99Va588475e233zYlXh0jwZSfSpUqJS1PxEoYrNsO9Yo0Eo/R5lDX6FZmCqFuNcL8aEfAcJNftmxZZSW98MIL2uXRzAy1a9dOLaFbs2ZNUrToZgj1QrdDJCE0nF0EX5sUsSYfKISaVASzoSeB999/X42Y4oHv3LmzHD16VM+MmpQruNRCWadOnZpqjBDA7NmzRzwPQhhJKCNebOOPFEIbYTMp9xCAm/wuXbooUahRo4agz8zrYd++fZI+ffqol9BhqSIsvUgBoorBLN0DhVD3GmL+bCVguMm/7bbbJF++fPLvf//b1vSdTAzWG/oG4X4/tWCM1Ae6OAt1DYQQ67vhOBev1M4PFYcdxyiEdlBmGq4ggCYcnCLg4cXUEfQN+iX0799flRs75kUTIJpwg5ZaQNMZliPOx2ew1ckxrpF/CqFBgu++JQA3+Y0bN1YPKTyrYJWInwK84UCgxowZE1WxDWswnm1FcS0EMbUmdVQZMfEkCqGJMBmVuwj88MMPgukd119/vZoq4oa+LLMJwyns7bffrgaEoo0bO9bhFW8Ac1iIOgUKoU61wbzYQsBwk48mW86cOdWmTrYkrGEijz/+uGBeJP4UogmwAmE9JvKnAWuQQhgNbZ5DAhYRgJt8TBTGw4wHEmuF/RqMPV9iGRBCv2AkEYtmdB1/QLAKdQq0CHWqDebFMgJwk9+0aVMlgNhzA16j/RwwPQh/Bn369Ikag2ENhpsXOGXKFBXnggULVJywGuGSDG79MWKM9zJlykjp0qW1Gz2mEEZ9G/BENxKA4OFhz5gxo2BlCAZGGESxgGUcy8ZREMBIfYPvvvuu2lrVaDYbuwjCgjResEJ1nEJDIeRT4UkCZ8+eVRZIkSJF1F4hs2bN8mQ54ylUt27dJG3atLJ+/fp4LvfkNRRCT1arvwsFN/lY6I+mHzZNgtcq9G8AAA2DSURBVCgy/JfAW2+9pbjMnDmTSAIIUAgDYPCjuwnATT62yYQANmjQIOqRUHeXOvrcHzt2TM3h8+IudNFTCH0mhTA0Fx51EQFMgMbKiKxZs0rx4sUFjhIYUhKoU6eOWkJ3/PjxlD/6/AiF0Oc3gJuLb7jJxxaT6dKlk2nTprm5OJbmfeTIkcpS/uijjyxNx62RUwjdWnM+zze2lXz44YfVw929e3fBJGmG0AQwdQjdBVg/zRCaAIUwNBce1ZQA3OSjjwsPNpp6mA/HEJ7A1atXlTftRx99NPxJ/EUohLwJXEEAbvKHDBmitpYsVKiQeHWjcbMrAytBsIRu165dZkftqfgohJ6qTu8VBq6wXn31VSlVqpSyAidOnOi9QlpUInCD5YzpRAyRCVAII/Phrw4SwOhvvXr11MPcsWNHgdNUhugI7Ny5U02a9ssudNFRCX8WhTA8G/7iEIEtW7YIhA/WDJZmoV+QITYClStXlgceeMDXTiViIUYhjIUWz7WUACw+TPPInTu35M2bl026OGn37dtXWYNe3G85TiSpXkYhTBURT7CDAHZPu++++5QVOGrUKDuS9GQay5YtUwzRP8gQPQEKYfSseKYFBOANBh5N0Axu1aqVYHSYIT4Cv//+u+TJk0e5voovBv9eRSH0b907WnJ4RO7atasSwAoVKgjWCTMkRqBRo0ZStGhROXHiRGIR+fBqCqEPK93JIsNqGTdunNonI0eOHDJv3jwns+OZtDGtCFb16tWrPVMmOwtCIbSTts/TgufiihUrqgd20KBBglUPDIkT+PrrrxVTLqGLnyWFMH52vDJKAljr2qRJE/WwYrOg/fv3R3klT4uGAFzfcwldNKTCn0MhDM+GvyRIAG7ysZk3PMPgYYUgMphLoHPnzmonvn379pkbsc9ioxD6rMLtKC48QqPPqmDBgmqvEE7lsIb6/PnzlZX9zjvvWJOAj2KlEPqosu0o6qJFiwSrGtBxj+VdFy9etCNZ36Vx4MABtRcLl9CZU/UUQnM4+j4WTH9p3ry5EsBHHnmE3k4sviPgixFL6DjgZA5oCqE5HH0bC9zkY0lXpkyZ5K677hJ6QLb+VsDG9GnSpKEvRhNRUwhNhOmnqOAm/+WXX1ZOP9EMxmcG6wlgJQ54v/LKK9Yn5qMUKIQ+qmyzioqNvB966CH1QHbp0kXOnDljVtSMJwIB9LcWLlyYS+giMIr3JwphvOR8eB28mWA9MCySmjVryrZt23xIwbkiY6tSLKHD6hwGcwlQCM3l6cnY4Ahh4MCBki1bNsmfP7+89957niynzoWaMWOG+gPiXExraolCaA1XT8QKN/l4ALFXMKzA559/3hPlclshvv/+e8V/zJgxbsu6a/JLIXRNVdmb0RUrVkitWrXUA9iuXTv59ddf7c0AU0sicP/993MJXRINaz5QCK3h6tpY4SYfwgcLEBOjN2/e7NqyeCHjzz77rFpCd/DgQS8UR9syUAi1rRp7M/bLL7/I0KFD5ZZbbpFcuXLJwoUL7c0AU0tBYMmSJeoPiUvoUqAx/QCF0HSk7ovwtddeU04RYAUOHz7cfQXwYI6xfwv2I4ZFyGA9AQqh9Yy1TQGrQOrXr6+sjieffFJ++uknbfPqt4xh+wIsofv777/9VnRHykshdAS7s4nCTf6//vUvJYDYMGndunXOZoipJyMwfvx4tYQOo8UM9hCgENrDWYtUMBEXO8Rhg5+sWbMKdo5j0IsAnFegi4JL6OytFwqhvbwdS23OnDnyj3/8Qz1kzz33nGP5YMKRCZQoUUJat24d+ST+ajoBCqHpSPWK8D//+Y80aNBACWDDhg3l8OHDemWQuUki0LFjR7WE7vTp00nH+MEeAhRCezjbngrc5Hfr1k0J4D333CMQRAZ9CcBiR5OYS+icqSMKoTPcLUsVbvKxFC5fvnySPn16mT59umVpMWJzCOzZs0f5c+QSOnN4xhMLhTAeappe8+abbwqWY8Gy6NGjh1y5ckXTnDJbgQSqV68u8OrN4BwBCqFz7E1L+YsvvhBskwkBrFu3rsDCYHAHgcGDB6vVPPDww+AcAQqhc+wTThlu8nv16qWawHfccYesXLky4TgZgX0EPvzwQ/XnxSV09jEPlxKFMBwZjY/DTf6LL74ohQoVUg8SPjO4iwBGhgsUKMAldJpUG4VQk4qINhuLFy+WqlWrKgHE6pALFy5EeynP04gAdvxDfy6DHgQohHrUQ6q5WL9+vWA9MPoBq1WrJlu3bk31Gp6gJ4GpU6eqeuQSOn3qh0KoT12EzAkmQPfr109uvPFGue2224T9SSExueYg/Dviz4xL6PSqMgqhXvWRlBu4yZ8yZYraKxgPDueYJaFx9Yfy5ctzCZ2GNUgh1LBSsDkS5pZBAJ966in5448/NMwlsxQrAcztvOuuu+T8+fOxXsrzLSZAIYwT8HfffaecmMKRqfHCsUTCxo0blbUAAaxYsaJg+0wGbxDAIBfq9dNPP/VGgTxWCgphnBWKf3dMfxg2bJhaxVG6dGl1o7dp0ybmGOEQddCgQZI9e3a5+eabZf78+THHwQv0JXD06FFVr6NHj9Y3kz7PGYUwzhvgwQcfVAIYePmkSZOUGH7++eeBhyN+njlzpsApAqwFrDJg8B4BLJ8LXkKH1gPqPPhFF1zO1D+FME7uuIHhMSQ4wEoMdTND8GrXri1NmjRRK0CwCgTfEc8TTzwh2KOCwXsExo4dq5bQwSoMDIa3GfxpBr64W10gJfs+UwjjYG38m4e6aWEp4hUY8DAE//Pje5kyZQTrhBm8RQCrRnbt2qXqFvX89ttvpyggulaC75MUJ/GAbQQohHGgRhMY/XmhQighxEhhsBDmzZtXHn74YeUkAc0mOE9t3LixNG3aVE2cxmhx27ZtpUOHDtKpUyflWxAPT+/evdW8woEDB6rtN0eMGKGm1sD11sSJEwV5w4TdGTNmyKxZs+SNN96QefPmCTzTLFq0SM1DXLp0qWADd6x1/eSTT1QH/po1awSTtjds2KD2MsZk3+3btwv8Gu7fv18g+rBqYLlis3eMZJ87d04uXryovNxwk6H/3g3w/m3UdYYMGVR9hrtP0L/MoAcBCmEc9YCmb7h/cwyaQLACg7Em2HhA8J4zZ07BnDJsnoRr4KL97rvvVtMr4EChYMGCyqcgJlHnzp1bnX/TTTepvUYwuRoPWbp06dQmP4HxOvE5bdq0yvFDpkyZJEuWLIJ8Yn9k5Bv5z58/v1oXfeedd0qxYsVUWVFmlB0MsFtblSpV5KGHHpKaNWtKnTp11O562MmtUaNGqusAS9JatWqV4s+hZ8+e0qdPH+nfv7/qY8UIPvZlGTdunLzwwgtJfwzomsAfA/ZpwWAU9m2GpYapSsuXL5cPPvgg4T8FYx/iwDooW7Zs4K2Q9BnnIK9oERivUC2MpAv4wVICFMI48OIhDvVvjhsZNzgsrsAwZMiQJCvBeEiWLVsWeErcn69du6YsMjhiwPy0M2fOyKlTp5TVBuvt2LFjyj3/gQMHZN++fcrC27Fjh2zbtk3QxN+0aZOyAmENrl27VvVXwZs1LEVYjOjLRHnwkGMKCARkwYIFMnfuXGVtQlxgfcIKnTx5snIGMWHCBCVEGCWFxYqN42HBwlqCaMFjTvfu3aVr167K2oXV265dO9W32qJFC2nWrJlyKwYRhBjCYoZ7sVq1akmNGjXUn1DlypXVWl3jzwTdDCVLlpTixYsrd/dFihQJ+WeSI0cOyZYtm2TOnFkyZsyoBDxNmjQp6seoJzPeg7dJRZ9gqHhjGWSL+4bhhSEJUAhDYgl/EE1C3MShblo8tBgsCRVgoZQrV05NlEYzlUEvAoF/KGjyo58Pu/6dPHlSdQcE/6GgDxBdB1jzvWXLFvWHArEPFrhcuXKlKGikrpUUJ/OALQQohDFiNv7Ng1d7oLkcTiBjTIKnu5gAmveBYghrOTjgXsGfJoM+BCiEMdYFmsS40Y3VJOijQp8YBk9CWYkxRs/TPUAAXQnTpk1T3Q+himNMxA/1G485Q4BCGCN3CKExMox3DIyEmk8YY7Q83ScEInWt+ASBlsWkEGpZLcyUVwkYXSsY3IFfSePFP1Nna5xC6Cx/T6eOUWljc3mj38zTBY6icJhZADEMfgX3OUcRFU8xkQCF0ESYjOp/BCCC6DvFwIDRd8qH/X98+EkvAhRCverDM7kJNbHcM4VjQTxHgELouSp1vkCR1mI7nzvmgARSEqAQpmTCIwkSwIRhWIRoCmO1iTHViE3jBMHycssIUAgtQ+vfiDHFCKOimC+H6UX4jgnE6DPkelr/3hc6l5xCqHPtuDRvxqRzNJEDA+ZdYvCEgQR0I0Ah1K1GPJAfY9J5cFHCHQ8+j99JwG4CFEK7ifsgPUwOhhux4EAhDCbC77oQoBDqUhMeygcGRbD2Oni1hNFn6KGisigeIUAh9EhF6lYMiCBWk2BXP4waG4MnHDnWraaYHxCgEPI+sIwARojRHMYLU2oogpahZsQJEqAQJgiQl5MACbifAIXQ/XXIEpAACSRIgEKYIEBeTgIk4H4CFEL31yFLQAIkkCABCmGCAHk5CZCA+wlQCN1fhywBCZBAggQohAkC5OUkQALuJ/D/iq1ZTD1oF74AAAAASUVORK5CYII=[/img][br][br]Explain how we know that triangle [math]ABC[/math] and triangle [math]DEF[/math] are similar.[br]
What does that tell us about angle [math]D[/math]?[br]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAVYAAAEnCAYAAADy0WvnAAAgAElEQVR4Ae2dB9QURdaGFxUDKgaMYNYVlFUBWVzFgKAsZtYEJsAEuiIGQDGLgWWRqAiIignEgIpgBBMSVcBAEkFEQAxgJBhA6z9P7V/Y9Ncz0z3TPVPVc+85c2amu7rq1lvVb1dX3br3L0pEEBAEBAFBIFYE/hJrbpKZICAICAKCgBJilU4gCAgCgkDMCAixxgyoZCcICAKCgBCr9AFBQBAQBGJGQIg1ZkAlO0FAEBAEhFilDwgCgoAgEDMCQqwxAyrZCQKCgCAgxCp9QBAQBASBmBEQYo0ZUMlOEBAEBAEhVukDgoAgYBUC33//vXrrrbcqfD777DOr9MymjBBrNnTknCAgCBQdgYceekj95S9/qfDhuCsixOpKS4megkCZINC6dWt11FFHOV1bIVanm0+UFwTSh8BBBx2kbrnlFqcrJsTqdPOJ8oJA+hBgGuC5555zumKpIVYmts2E9/vvv+90o4jygkC5IvDmm2/qudUrr7xS3Xrrres+Li1c0XapIVbmZfwT3o0aNVKsMIoIAoKAGwgwBbDVVlvpOVbmWc3HDe3/1DI1xLr77ruvNy/DqJUGgnBFBAFBwA0ETjnlFMXHdUkFsTIqZbTKa4RX0rC66K2P/BYE0o6Af4Dkan1TQaxmXsb/2k8jyYjV1a4pepcbApkGSC7ikApiZV5m6623Xrd41bdvX8X8KmYbfrJ1sZFEZ0GgHBDAEoA3zzRIKmrBnAyjUya6IVMap3nz5kKqaeihUoeyQYABkn8BOmiKzwVAUkGsLFL16dNnHd6MUiFZRq0igoAg4AYCLDgzref/uKH9+lo6T6zYtwU91cx+4/WrK/8EAUFAEEgeAeeJNdO8zBVXXKHNrZKHUEoQBAQBQWB9BJwnVgiU136vMFplMcv1/cbeOslvQcB1BLp06aJ23XVXtffee6s77rjD9epk1d95YoVU/RPezLnaRKrMHeXakhcmjb8lmUtmG6+IIGA7AkELUwMGDLBd7bz1c55Y/RPduQgsb6TyuBDia9OmjSb+bERvOl22NP7iIeI6derovP3n5L8gYBsC+++/f4UBUNOmTW1TMzZ9nCfW2JCIOSNDfJiCZXKDBvEae1s2MoQlVjPVwTQIo3URQcB2BI444ogKxHrmmWfarnbe+sldmTd02S9kUc0QJdMV5rf3KsgXcjTmYUFpvOnNb0jYjNSFWA0q8m0zAo899lgFYn3llVdsVrkg3awm1p9++kldfPHFesIbcnLVR2MmYvW2XJg03vT8hlyFWP2oyH8bEbj99tt1Xz300ENVpUqV1KhRo2xUMzadrCbWk08+ucJT7sMPP4yt8sXKKAxphknj11eI1Y+I/LcRgaVLl+r7mEHS888/r3+7eB9HwdZaYl2+fHkFUmV0dskll6hffvklSh1LnjYMaYZJ46+IEKsfEflvIwLnnXeeqlq1qpo/f7766KOP9H396quv2qhqbDpZS6wrV64MJNYNNthAH69du7Y699xzVa9evfQrMfOUtkoY0gyTxl8/IVY/IvLfNgTGjRun79c777xTq7ZixQr9/5FHHrFN1Vj1sZZYqeWll166Hrluv/32asGCBWrSpElq4MCB+vxhhx2mNt98c51ur732UqeddpqiEV966SXFK4gNEoY0w6Tx10WI1Y+I/LcNgX/84x/aKub3339fpxpvnv/973/X/U/jD6uJFcA7dOigSbNZs2bq448/ztgG06ZNU5ghESvn6KOPVttuu62+buedd1YnnHCCuvHGG9UzzzyjPv3004x5JHUiDGmGSePXT4jVj4j8twmB+++/X9+Djz/++HpqQazcp2kW64n1qaee0o0zduzYyO0wa9YsRaNee+21CmKGZGnUbbbZRjVu3Fh17NhRDRs2TM2cOVN5n6iRC8pxQRjSzJSGznn44YerxYsXVyhFiLUCJHLAEgT++OMPVa1aNe2+068S21pbtmzpP5yq/9YTa//+/TUZYvMZhzBiZeR6880369g6e+yxh85/0003VZiCXHbZZeqBBx5Q7733nmKeNw7JRJrevDOlQR8eBkEPFiFWL4Ly2yYErrnmGt1vJ0+eXEGtI488MvUuPa0nVozmIZYlS5ZUaKC4DmBp8Oyzz+q52RYtWqhatWrpMim3bt266oILLlD33HOPevvtt9WyZcviKjZUPizKYaJS7sJWZcIhs1OND79t2r5c7u3jrf8nn3yi759Mr/tscKlZs6b3ktT9tp5Y//3vf6vttttO/frrr4mAP2/ePNW7d+8KebM5gVEiVgetWrVaF5kAsoV4zzrrLHXXXXcpzEYWLVpU4Xo5EB8C3IjgzvZgHrR82CbMnLqIfQj861//UtWrV1dfffVVoHI8FHGU9PPPPweeT8NB64n19NNP10SWFNiMBl9++eVQ2TMPO3HiRMX0BMbODRo0UJtssom+6QkNQ4e67bbb1MiRI9XcuXND5SmJsiNg/OrGNRWUvTQ5WygCL7zwgr4f+vXrlzErTK14UGLhk1axnliZe8SBQ1LStWvXgqcZPvjgA8UiU/v27bWuGEPTcXbccUe9aHbdddep4cOHK9IlNfJOCp9S5mvmkPkWcQOBv/3tb6phw4ZZlWVKjfuDQUpaxXpixd0YI8EkhG112Z6shZTJFAOOJ7A8OOaYY9QOO+ygOxOky8PiqquuUkOGDFFM7v/www+FFJXaa3n1BysRNxAg7hyEmcsPABYupGMROa1iPbGyKaBt27aJ4H/vvffq1f9EMg/IlA0LLJLdcMMN6sQTT9TOZehglStXVocccojerotOb7zxhvryyy8DciivQ2Aj86hutDlrEhtvvLE655xzciqMKRZtS19Pq1hNrExu0wAQUdwyY8YM1aNHj7izjZzfjz/+qBfAmJtl19g+++yj60y9DzzwQMXCTc+ePdWLL76Y6jkpP3AyDeBHxO7/LDIzQOC+CiP0bzbtpFWsJlbMaWgAb2jruBoCUmXO00ZZu3atmjBhgibUs88+W+EXARz4/PWvf1WYhOGGbcSIEYpNEIwA0iaGWGXRyv6WZddjVKLccsst1UUXXWR/5fLU0Gpifeedd3SDDR06NM/qBV/GyqWLTiAgGXwknH/++apevXpqo4020viwkwUXi9dff72e1506dapatWpVcOUdOUpduVll4cr+BmMNgQd+lA01vI0xHZZWsZpYjelGnC7GWLDCDhIvO2kQjLEfffRRxauY1yENtr/HHnusXiQbPHiwGj9+vMIVo0uCrSNTISL2IvDEE0/oB+CDDz4YSUkWJuvXrx/pGpcSW02srJozauFVIw7BkL9z585qzpw5cWRnbR5ffPGFXnGlrl6HNHgBw3SNnWZYQ4wZMybQB4EtFWPhivZv3ry5jkZLRNqHH35YRrG2NJBSCvvtfIICsiurRo0aFtUkXlWsJlZci3FjxbGziRV5dnxMmTIlXgQdyQ2TLmIMgYHXIc2GG26oRw6MDLt37663zzIKtkUIx4PJFaNX+gK/XQ3RYwumcelhwq1gxRJVeLDT97755puolzqR3mpi7dSpk3b/V+jWN3Z44HSFBSGRPxFYs2aNniJgay4WCcYhDQTGghlRNJk24XWPKZTffvvtz4vlV1kjYMKttGvXLi8csHWln6U1RIvVxMoe/X333TevhjMX4aUKY3y+RcIhMH36dDVgwAB18MEHq7333lvfANwE/D7ppJMUnot4TWf0j7mYSPkhQLiVrbfeOm8TwLSHaLGaWI877ric2+OydWl2dhBNoBTOrbPp5co5CHT16tVaXXwfYElBVIc6deqsI1ucbbAqfPnll2syZhU/k/MNf72ZCzb5+8/Jf3sRMOFWmDrKV5ia4mHtonVOmDpbTaysGrJ6GFWwT4VQ2Z8ve/Ojove/9BAeDsKzCa4csaVlyob94cYhDY7E+Y+dIt7BCJPjdfFHUDl8cnJj8bn66quzFSPnLEOAcCu40yxUaPu0hmixmlh32223SEbERALgFZadSvxOs2Dn6SWrbHUlLSvqUQTTLHaDRRX8x+ItjDltVouNQ5rNNttM296y5RFfnIZUzTd+FUTsR8CEW3nyyScLVpa2z+SzteDMS5yB1cTKzYhnqGzCJDpmQ7yWMDpiU0EY4ZXV5siuQXVAX1b1mdsyhMRvjvmFtHRab1oWooxAtrjk4xO0H5/X+W7dupnkBX2z6MXrI6MTTKeM7t5vnImL2I0AOwIJt3LqqafGoigDp7SGaLGWWM0cTJcuXfQEOfOk2J++++672mwIMsDlH6MqXkd5vcwlkE2bNm30jY39HTc23uizjfwgI9J5dwCRD4TEOS9Z5Sq/0PPoydQIpGgEvdDPT444gubj1dtcw7fX8J5rvXly/uuvv1Z33HGH95KCf/PQI9SMCWHuJda4yypYWcmgAgIm3ErYwUuFDHwHMJ3j/kujWEusRGTlxoMA+vbtqw3a2c7JKyMOSdi2GdUGDhKEbAyRQpAQVaZ5XMgG+0k/QUGqRsgrCV8GJv8w33RQr04QJQ8O6hckfp1J539AsNp/0003BV0e+RhvFOeee65uTxa7WFH2kiquIb/99tvI+coFxUPAhFvBDWZcwiAnrSFarCVW5gS5+Vj4iEsgID+BYGxOOX6BbFj9hjQhV+/Iz0tiXOf/788r6f+QqJfc/UQbVL53xMq15mFj0uLYhXoV4uDl6aef1uZZ4ItdrDcMMguM2M+yu07sYw3q9n7jE3mXXXaJNeYbU1jcW2ls/4qMYknbmj3IcdqfQib+Vw+OQUR+gVTMSBZi8BOrGQ1y3P8a7s8rif+Uz8OHOUtG1EYfykJfHhjoRX1Jw1ZQr0CkPGT4eOvmTcM0S9S3Aq5n3ziYogdbaNnxJeIuAsZnBwE14xRMregjaQzRYi2x0oiAvnDhwtjaEvKBhCAb4lIZUvKP1iAanqSGrNDDSz4cZ5QHKZWCVA1poRejav/8qDnOQwO90ZVRLa9eUYQw4P68M12PFQFBGY2NK9624pqLy1SmHC8OAoRbSSI8UppDtFhLrJjrsKIdxRVZmG7GSM67Uu4lTK6HNDnvPe4n1jDlFCMNpAdp8hDg2wj6+qc8SMvxsERJXkSpzbUvn0VFytpzzz11/pC5Tb4GDCbynR8C9Cv6DaPWuAUfIOSdxhAt1hIrHpjw8RinMLqEhPiGQCEE/ntJiNd//5wpje8l2jh1iiMv9OdhYCSTvpmOm+v837wtZNpdA0GzVRjzG/LFtMs1t4T++sr/9RHAModwK2wtT0LYvEPfSWOIFmuJFacghx56aKztaUjVmymESeNCFBCuIQkm1s2HY7xGB9mLevMq1W8zajXl89ofNEVBPaI+IDBpY+upEeZ1sTnFyTZe4JmHJSy4SPoQwMcvu+mIUpGU0CfTGKLFWmJlyyMOP+IS5lFpxKBXYUM4kBHzl/4P55mb5XgpxT8XjC6MvJnXNAttHKMeeKrinBFDvt5j5ly2b7wQ8Xn++ee1ByywwI9m3AsZ2XSQc8VHwIRbYUouSWFnXhpDtFhLrLVq1dIjozgb1T8XSd7G3CqItEzZhnjN/1J9m1d+Ft8YPfPNFECQzSoPAc4x0iYddc81XxpUr/79+6+bP91vv/1U3GFygsqUY6VHAMc63IOFuuzMVRMGLGkM0WItsTJ3x06POIWRHATDCA9iMtsrvQs/QeXZQqzoxqs8BMsHvYNG4KYOECnpqHe2B4dJ7/2GUBs0aKBH+YR8idOe2FuO/LYPAWPqSL9JWnjTSmOIltDEyg3M/FrQJ9vNzatn0DW5XkkhMwzI4xbKjUo4kFkufePWsxT5sfiEfwDjJIWRxOTJk0uhipRZQgR4A8JlZzEkrSFaQhMrr5aQXdAn29wjI6aga7ItouAAhGv8Ru3FaOhyLAPzKFwE7rzzzhp3tpyypVik/BAw4VYYDBVDTIiW7777rhjFFa2M0MSaSaNMK9AmPcSajXhNOu832x0h1iRs57zllPtvRqOYtVWpUkWv8nfo0CGvnVbljmNa6o9/Xe47nJkXS9IaoqUgYjVzltlekyFWv11orkZjCyQNLDt3ciGV33nwPfvsszXG2267rZ5vJv6VSHkjwJsKaxuff/550YCYMWOG7odxhrgvmvJZCiqIWFnRgzizCaPVXGn81zMFALFKSBU/MoX9xznxCSecoLFlpxSvYSKCAAiYcCs9evQoKiDLli3T/TFtIVryJlbmSCG/XKvNECs2lZj8sBrPdy6zH3b7YN/2008/FbWR01rY4MGD1eGHH67bi4fho48+mtaqSr3yRIBwK6VanYdH0haiJW9ihTDZF55LsBiASCFiPoxeATKbiRMxkIgIKlIYAoSoOfDAAzXeONGQOevC8Ezr1SbcCm4eSyHwQdpCtORFrGFHq5kaCVIFzEzCXM8hhxyS6bQcz4IAJlM4qGZREYx59Z84cWKWK+RUOSPAfn3mVU8//fSSwZDGEC2Z2S0LzJl8mGa5ZL1ThpjXO+j506xZs1TuxvBUMfafmEyxqs9uKwiVoH2zZ8+OvRzJMF0ImHArROQolfD2yxRhmiQysTKnyo0LOeYrWBNkG7HWq1cvsu/QqLpks2SImlcp02MyxbZV4khhNtW+fXv15ZdfllIlKdsRBEz4o86dO5dUY/pv2kK0RCZWRqssgAQJi028wnuje0KiXhKDkBlVZbMU2HXXXXWs+qAysh1jLtc4Woa4eRJ6hflenoyc40Na/64xpinQjY9Xb28+Nvwm7hfhMqjHTjvtpMNN81onIgiERYD+w5RRqY3z8aDGVvM0eUmLRKxmtJppD/GHH36ob3TvfA0kbIiMbwDMRqp0ik033TTyKqGxqYUYMxEinYgHA/Xgw28sFoyQhyFa8ohqf2vySfKbFf3GjRtrTPfdd9+si4BJ6iF5u42ACbcyYMCAkleEPg03FNN+NulKRyLWMMrgdd4fcROSYqQKmeWSX375RYNM3KSwQv6MgrOZcXGOxvOTLkRvHhR+wod4bZG7775bm8NQB8xiZLuvLS3jph6EW/G/0ZWqJuPHj9f3ZpoWWWMn1kIbB6/1kAdb3cIKo1RGo9kE0gzqSBwzBGrjiJW920RSAJMmTZpov6jZ6innBIFcCBirnJdffjlX0qKcnz9/vu7faQrRYh2xTpkyRYMcxasSxMiH13jcATIZ3rdv3/VGpxBoELH6CdeGOVZMplhQ2GGHHTQWzIXxVBcRBApFgPlUwq1wj9giK1as0P08TSFarCNWPNUzOps3b17odocwWZQyW2whR36zOGVe/Unjf9WnAD+xhi40gYSYTLVt21bPMVeqVEk/LGbOnJlASZJluSJAuJXNNtvMOu9l3PNpCtFiHbHed999OpYSgczCCqTJVIAhUXMdxyBZxGZiZXTeokUL/UBhrvjyyy9fL86UqY98CwKFIICtKgTGKrxtkrYQLdYRK42Og5Aokok0OW7mT/nmv18yHfenS+I/JlM4FKazs/vkhhtuSDwURhL1kDzdQIBwK/vvv7+y0ZMZb5hpCtFiHbHiC/Lvf/97pJ7K67w3mJ652Eu4jFy9plUmDaPaoCkCcz6Jb8xLCHcCobI626tXrySKkTwFgXUImHArtjrgIUxSqZzArAMpxh/WESsLNccff3ykKhr7WmODysXmmDHBMv+NaRVpzNZa73WRCo6YmAW12rVra0KFWIcMGRIxB0kuCOSHAAMI/EbYKldddZWO/murflH1so5YcW/XqlWrqPXQxvzMT+Ilhw+/zTSAyQxSxW6VpyOrokFpTNo4v3GKwm4yRqj4QTBkH2cZkpcgkAkBE27l7bffzpSk5Mex095www3Vjz/+WHJd4lDAOmJlz3DHjh3zqhsjUF7r+fA7SMKkCbou6jFMpti3z6Q8hHrmmWdqZ8JR85H0gkAhCCxatEj3P/qizTJ69Git56xZs2xWM7Ru1hEroUIwhMe7/VNPPaXDs/h3coWuXQkSYjKF20PIdJNNNlEXX3yx+uijj0qgiRQpCCjdF7fffnvrrUymT5+u75m0hGixjlghJF4LsGMlXAQhG7BvY4HnjTfeUBgT2yiYTLGAhv50ZEbdixcvLrqqzCX7zc6KroQUaAUCRFqlP7qwOPrFF19oXdMSosUqYsV2lY4wcuTICh1z7ty56vHHH9dzqSNGjKjgj6DCBUU6gMmU8ZhF1APMxVatWhV76ZAlGx6CTMY4x44z5ozBj0+Q5y6vUmbhzqT3f2eaSvHmIb/tRoBwKw0aNLBbyf/Xbu3atbrfpiVEi1XECnlyg0+YMCFjZ8A1IfMxeJ4q5V5nzFbq1q2r9cV/rNmIkFHxAk5AcpAmI+IgYmUxjOPGugGiZeEuyLzMqEEa8vV/mJ+mDTgv4i4CJtyKS/vv6XdpCdFiFbGaSJEQbC5hcYjXBuI68fpbLMFkipEpnYCRahQvXPnoCMFhKoNFA6QXRKxB+RrzsqgjT/L3W1ME5S/H7EXg559/1uFW2M3nktDPW7Zs6ZLKGXW1ilgJz7z55ptHcryL0xbmM7ONcjPWPsIJTKa22247Tagnn3yyKuZIwIwekyZWRrw8MIr5oIrQBJI0JAIm3Ip5gwl5WcmTMVDhkwaxilixBOCpFVWWLFmiHWMz3xmnMCq+7LLLVOXKlTXhnHvuuRnNuOIsN1NeUYiVtFGxZKQatIMtkz5y3D4EiHPGw/Haa6+1T7kcGp1//vmpCdFiFbFed911eW9rY8EIawK8YxUqmEzxSkIH3XLLLRUegT744INCsy34+rDEykiFOdkoGxHynToouFKSQawIsHMRXxusRbgmt912m97A45reQfpaRaw8sdiZlK8Q84k50Hxt4TCZatq0qSbUGjVqqC5dulgVLiIMsRpSJW0UYbSKIwwRdxEw4VYGDRrkZCUee+wxfe9heuW6WEWseHrCuL4QwWSLJ9+0adNCZ8MUAqYpjFD3228/9Z///MfKJ34uYmUuFkuAqItPXMcI1+tHITR4ktAaBHDoQzw0V8XY3bJu4rpYRayYL+GMoVBhcwFzTMyRZhNMpiBSCJXosrZ7MM9GrJAjtqtRSRV8yDfqfGw2XOVc8RHA3I9+nO/bWvE1rljinDlzdB2KuTBcUYt4jlhFrLx+33nnnbHUbMyYMRlNoZguqF69um7EY489VvEK4oJkIlZDqrmiyt51113qtddeW6+qZrSapB3uegXKn9gRWLZsmQ63csEFF8SedzEzJGwMDwfbBzhhMLGKWInFM3jw4DB6h0qDjSt7kI1gMrXFFlvoxiNEdxwLXSbvYnxnIlazldaYq3i/Ddma0ORMt3gFQsXjFwQr4iYCLK7SrwnK57pArGkI0WIVsQLqs88+G1vfmDFjht7qickUeW+00UaKp3pUo/nYFCowI/QOmgc1mwcgXv/Hmx4chg8fvp4WnI9iPbDexfKn5Ai8++67um/jGjANwkP+oosucr4q1hDr119/rTtIXNFIvSZTeMxiq5x39Op8y0kFBAGlFOFWDjjggNRgwTpBGkK0WEOs5lWVCexCxGsyhT3fzTffLDuJCgFUrrUWARNuZejQodbqGFUx7HDTEKLFGmJlNXPTTTdVTMTnI5hMHXzwwXrUiz0m86tRIr3mU6ZcIwiUEgEsOU466aRSqhB72VdffXUqQrRYQ6w4VCFSaVTBZIqRKXOoRxxxRKyLX1F1kfSCQLEQMOFWJk2aVKwii1LOPffco0O0rFy5sijlJVWINcSKH0bc74UVTKaYO4VQCZKGAxcRQaAcEDDbjzt06JC66mKpwz398ccfO123ohArRusE78smbAxgO2kuwWSKoGOAf9ZZZ5XUJ2suXeW8IJAEAuxO3GmnnRQLvmmTd955R9/bfntr1+qZOLFizgMJ8skmZ599tjrnnHMCkxgvU+RRpUoV1a5dOzVx4sTAtHJQEEgzAoQn4j5I64aOhQsX6vq5HqIlO9vF0EOZYMdInc6QzQgdo3ZjzG6K9ZpM8YTGzyS2qSKCQLkigE8LPmkVnHTDFa6HaEmUWHmqmj3ogBVkmI+BM6TK+R133FFHZvWaTO27777qjjvusMrLVFo7tdTLbgRMuJWgmHB2ax5NO7jA9RAtiRGr2YNudv4AVtAOn1q1amlS5bz3gy0b/lWzjXKjNZekFgTcRQB/w9WqVdPrCu7WIpzmeGhzPURLYsTK1kozWgVObEs55hVc+3nJ1Px23ZmEt47yWxCIAwGmwVi0LYepsKOPPtr5EC2JECvmIPj3ZDiPj0U+bFXzz6GaiWpDqObbNecocdw4kocgkAmBmTNn6gHI9ddfnylJqo4zsKpZs6bTdUqEWDGvMiTp/Q6KMIrDBW+aI4880mlARXlBIG4E2OZJZODVq1fHnbWV+aUhREvsxGoiffoXqpgGYNQaJOyeuuSSS/ScatB5OSYIlCsCo0aN0gMPFq7KRUyIlq+++srZKsdOrIxKg0amLFwxMhURBASB8AgQbgUPVuUkOKmHK6ZOnepstWNlOkapABIUz9yck1V+Z/uKKF5kBDBX5H56/fXXi1xyaYsznu5cNiuLlVgZlRrzKn/TQKhMB7CwJSIICALZEWC7KhE1Lr744uwJU3jW+GZ2OURLrMSawjaWKgkCJUGAcCtVq1ZVWM6UozBSdzlEixBrOfZaqbPVCBD+GWLp1q2b1XomqRzmmi6HaBFiTbJ3SN6CQB4IsFjFhppyFtdDtAixlnPvlbpbh8Djjz+uR6v+oI/WKZqwQq6HaBFiTbiDSPaCQBQE2AbevHnzKJekMq3rIVqEWFPZLaVSLiJgwq3g8a3cxYRo+eWXX5yEQojVyWYTpdOGwKeffqqnAIikIaLUiBEjNB7z5893Eg4hViebTZROGwKEW6levbr69ttv01a1vOozfvx4Taz+rfF5ZVaCi4RYSwC6FCkIeBEgvhPmVf369fMeLuvfRA8BE/wGuChCrC62muicKgQItdKwYcNU1anQyvz444+aWD14Cc8AABgoSURBVF0N0SLEWmgPkOsFgQIQGDx4sCaQF154oYBc0nkpI1ZXQ7QIsaazT0qtHEBgxYoVOtxKpujEDlQhURVdDtEixJpo15DMBYHMCBBupXLlymrOnDmZE5XxGZdDtAixlnHHlaqXDgHjGs9lRyNJo+dyiBYh1qR7h+QvCAQgwJZNQrv/+uuvAWflEAiwYWKrrbZyEgwhViebTZR2GQEcOLMwM2TIEJerkbju4ANOy5YtS7ysuAsQYo0bUclPEMiBAOFWmjZtmiOVnH7xxRc1sQZFJLEdHSFW21tI9EsVAr1799ZkMW7cuFTVK4nKEPOKEevo0aOTyD7RPIVYE4VXMhcE/kTgyy+/1OFW2rVr9+dB+ZURgcWLF2tiHThwYMY0tp4QYrW1ZUSv1CFAuJVtttlGQRgiuRH47bffNLG6aDkhxJq7fSWFIFAwAhMnTtQk0b1794LzKqcMXA3RIsRaTr005XUlEnDfvn1Vo0aN9AeH0X7vSEQJNue935miC2eC7JRTTlFXXHFFptMVjhNupW7duhWOy4HsCIDZiSeemD2RhWeFWC1sFFEpPwSIE3XUUUcpwrBDqIRbZ/HDS6785hjnvB9vmlylcx32lZQVRoYOHarLfPrpp8MklzQeBE499VRVv359zxE3fgqxutFOomUIBBix+oWRJR8jhljN/6jfXA+pMloNQ6y///67ItwKBCESHYGOHTuqGjVqRL+wxFcIsZa4AaT4ZBFgdOklQF75vf+jlA5x4xiEEbE/30z53HbbbXq0On369ExJ5HgWBPr06aM23HBDtWbNmiyp7DslxGpfm4hGMSLAaBESNMJvpgzeeust/YlifM7It3Xr1jqrMMQ6b948TaqMukTyQ8BErWVu3CURYnWptUTXSAgw2uG13TtFwDHmWCFXPvxmFJqLYBmlQtImrzDESriVXXbZRf3www+R9JbEfyLwxhtv6DYiVItLIsTqUmuJrqERgCj9C1dBF0OUjEIx6zGk6U/HaInz3gWuXMQ6ZswYXf69997rz07+R0Bg1qxZGsfhw4dHuKr0SYVYS98GokHMCECqEGFYEyoINRsJMycLkXolF7ESbuWII47wXiK/80Bg+fLlum169OiRx9Wlu0SItXTYS8kJIBCVVI0K2YiVc9k+ftIdNGiQTv/KK6+Y7OW7AATA3rUQLUKsBTS4XGoXAvmSKvOn3LzeBZIpU6ZkrVymEStB8KpVq6ZatWqV9Xo5GR6BPffcU7Vs2TL8BRakFGK1oBFEhcIRMPOgderUUbfeemuFjyFN5lM5j09UPoyEmDbwjjrvueceTbQY9meSTMRKuJVNNtlEEb5ZJB4EGjdurHfLxZNbcXIRYi0OzlJKwggwWmUuNNOH8wijU8ymTDqI1rsoRRp2SGGUzop0JmH+1r+llTIY+XpJOtP1cjw8AhdeeKGqWbNm+AssSCnEakEjiArpQIBwK7Vq1VLsthKJD4GuXbs6F6JFiDW+9pecyhiBZ599Vo9WH3300TJGIZmqm8XATOZwyZRaWK5CrIXhJ1cLAhoBwq0cd9xxgkYCCJjFxRkzZiSQezJZCrEmg6vkWkYI9OzZU49WJ0yYUEa1Ll5VJ02apPF96aWXildogSUJsRYIoFxe3gh88cUXOtwK0QFEkkFgwYIFmlgHDx6cTAEJ5CrEmgCokmX5IAChYrdKPCuRZBBYtWqVJtabb745mQISyFWINQFQJcvyQADHIJhXMRUgkiwCxAq76KKLki0kxtyFWGMEU7IqLwQIt+Kid3sXW6levXpOhWgRYnWxl4nOJUcAsypGq5hZiSSPwGmnnebUQ0yINfk+ISWkDAHCMuOb9YwzzkhZzeytjmshWoRY7e1LopmlCOBrgNHqhx9+aKmG6VMLt4GEaPnjjz+cqJwQqxPNJEragsDcuXM1qeJsRaR4CDzyyCMa90WLFhWv0AJKEmItADy5tPwQINwK0wArV64sv8qXsMb4tuUtgc0CLogQqwutJDpagcDLL7+sb+777rvPCn3KSQnjOeypp55yotpCrE40kyhpAwKEW2nUqJENqpSdDkuXLtUPtd69eztRdyFWJ5pJlCw1AgMGDNA39tixY0utSlmWz6JVpUqV1NVXX+1E/YVYnWgmUbKUCHz33Xd622qbNm1KqUbZl73XXns5E6JFiLXsu6sAkAuBTp06qSpVqiicgYiUDoEmTZo4MxUjxFq6fiIlO4DAtGnT9BTA7bff7oC26VYRXwGuhGgRYk13X5TaFYgA4Vb233//AnORy+NA4MYbb3QmRIsQaxwtLnmkEgGCCmI7OWzYsFTWz7VKmei5P/30k/WqC7Fa30SiYKkQINzKCSecUKripVwfAtiw8qCbPXu274x9f4VY7WsT0cgCBNibzk08ZcoUC7QRFUBg3Lhxuk3GjBljPSBCrNY3kShYbAQWL16sw61cfvnlxS5aysuCwMcff6yJdciQIVlS2XFKiNWOdhAtLELgkksuUdtvv71atmyZRVqJKoS/5i2ia9eu1oMhxGp9E4mCxUTAvG726dOnmMVKWSER2HbbbdXFF18cMnXpkgmxlg57KdlCBAi30qBBAws1E5VAwJUQLUKs0l8Fgf9H4OGHH9avmqNGjRJMLEXAlRAtQqyWdiBRq7gI/PLLL9rPaosWLYpbsJQWCQEWFGvUqBHpmlIkFmItBepSpnUIELOehZFZs2ZZp5so9CcCd9xxhw7R8ucRO38JsdrZLqJVERGYM2eOJtXrrruuiKVKUfkgcP/99+u2wj+rzSLEanPriG5FQYBwK3vuuadiOkDEbgRGjx6tifXdd9+1WlEhVqubR5RLGoEXX3xR36gPPPBA0kVJ/jEgAKEyZfPMM8/EkFtyWQixJoet5OwAAoRbady4sQOaioog8Pnnn2ti7devn9WACLFa3TyiXJII9O/fX9+kb775ZpLFSN4xIsB0DSFaOnfuHGOu8WclxBo/ppKjAwgsX75ch1vBebKIWwgQouWss86yWmkhVqubR5RLCgGC0m2xxRZq0aJFSRUh+SaEgAshWoRYE2p8ydZeBN577z09BdCtWzd7lRTNMiLQunVr60O0CLFmbD45kVYECLdywAEHpLV6qa/XNddcY32IFiHW1HdDqaAXgSeffFKPVvkWcROBXr166TZctWqVtRUQYrW2aUSxJBAg3MrJJ5+cRNaSZ5EQGDp0qCbWuXPnFqnE6MUIsUbHTK5wFIHu3bvrG3Lq1KmO1kDUBoGxY8fqdnz99detBUSI1dqmEcXiRGDhwoU63MqVV14ZZ7aSVwkQmDFjhibWRx55pASlhytSiDUcTpLKcQTatm2rdtppJ0V4DxG3Efjmm280sd55553WVkSI1dqmEcXiQoCdVewvJy69SDoQIETLpZdeam1lhFitbRpRLC4ECLdy6KGHxpWd5GMBAgcffLA66aSTLNAkWAUh1mBc5GhKEHjwwQf1aPWll15KSY2kGiCALXL9+vWtBUOI1dqmEcUKRWD16tU63MrZZ59daFZyvWUIEKLc5hAtQqyWdRhRJz4EbrzxRh3Gw2Z7x/hqW1453XLLLVaHaBFiLa/+WDa1nTlzpp4CuOmmm8qmzuVU0QEDBuj2/frrr62sthCrlc0iShWKAK//++yzj1q7dm2hWcn1FiJABAEsPaZNm2ahdkoJsVrZLKJUIQiYuEgPP/xwIdnItRYjMGHCBE2szz//vJVaCrFa2SyiVCEIEG4FEyuR9CIwb948Taz33nuvlZUUYrWyWUSpfBEgFhKviOPHj883C7nOAQRWrFihNthgA9WlSxcrtRVitbJZRKl8EGCrY7Vq1VS7du3yuVyucQyBvffeW5177rlWai3EamWziFL5IICDlapVq6qlS5fmc7lc4xgCRNdt1KiRlVoLsVrZLKJUVATeeecdPQXQo0ePqJdKekcRIKBgzZo1rdReiNXKZhGloiKA8+qDDjoo6mWS3mEErrrqKmtDtAixOtyxRPX/ITB8+HA9WsW2UaR8EDCOy3/99VfrKi3Eal2TiEJRESDcCk45RMoLgYceekg/UD/99FPrKi7Eal2TiEJRECCENeZVH3zwQZTLJG0KEMBjGW0/btw462ojxGpdk4hCYRFYsGCBDrfSqVOnsJdIuhQhwHZWiJXggraJEKttLSL6hEbgoosuUtWrV1c//fRT6GskYXoQWLJkiSZW5lptEyFW21pE9AmFABE6Ga0MHDgwVHpJlD4E1qxZozeEtG/f3rrKCbFa1ySiUBgEmjRpoho2bBgmqaRJMQJEEWjevLl1NRRita5JRKFcCNx///16tDpmzJhcSeV8yhE44YQTrAzRIsSa8o6XtuqtXLlSh1tp1apV2qom9ckDgQsuuMDKEC1CrHk0plxSOgSuv/56VblyZTV//vzSKSElW4PAddddZ2WIFiFWa7qIKJILgY8++khPAXTt2jVXUjlfJggYN5HLly+3qsZCrFY1hyiTDYGWLVuqfffdN1sSOVdmCDzxxBP6YWvbBhEh1jLriK5WlxActhqDu4ppGvR+8803db944YUXrKqOEKtVzSHKZELgkEMOUc2aNct0Wo6XKQKzZ8/WxDpo0CCrEBBitao5RJkgBPr06aNvnsmTJwedlmNljMC3336rF69uvPFGq1AQYrWqOUQZPwJfffWV3l1z2WWX+U/Jf0FAI0CY8zZt2liFhhCrVc0hyvgR6NChg9pmm23U119/7T8l/wUBjcARRxxhXVReIVbpnNYiMGnSJD0F0Lt3b2t1FMVKj8Dpp59uXYgWIdbS9wvRIAMCJ554oqpXr16Gs3JYEPgfAkwTbbXVVlbBIcRqVXOIMgaBYcOG6dEqZlYigkA2BG677TbdV9auXZstWVHPCbEWFW4pLAwCv//+u6pdu7Y644wzwiSXNGWOwH333aeJdeHChdYgIcRqTVOIIgaB22+/Xd8oM2bMMIfkWxDIiMDIkSN1f5kwYULGNMU+IcRabMSlvKwI4Fxl4403Vl26dMmaTk4KAgaBKVOmaGJle6stIsRqS0uIHhoB3MDtuuuuavXq1YKIIBAKgc8++0wTa8+ePUOlL0YiIdZioCxlhEIAx9X4A8CRtYggEBYBHsLbbbeduuKKK8Jekng6IdbEIZYCwiLQqFEjddRRR4VNLukEgXUIHHTQQeq0005b97/UP4RYS90CUr5GwKzsEiRQRBCIikDTpk0VjnpsESFWW1qijPUgfPXuu++umF8VEQTyQeC8886zKkSLEGs+rSjXxIrAtddeqzbddFNlkx1irBWUzBJHoFOnTlaFaBFiTbzJpYBsCOD5nQWrO++8M1syOScIZEXgrrvu0v3ohx9+yJquWCeFWIuFtJQTiMCZZ56p9ttvv8BzclAQCIvAo48+qol15syZYS9JNJ0Qa6LwSubZEHjuuef0zTB8+PBsyeScIJATgVdffVX3pVdeeSVn2mIkEGItBspSRiAC9evXV3iwEhEECkXATCnZYgMtxFpoi8r1eSHQq1cvPcJ49913K1zPTho8wm+99dY6DXOwXvn+++/VlVdeue58nTp11Pvvv+9Noggyd8stt+gP+YmkGwEiTWy44Ya6vW2o6fo91gaNRIfUI7B06VIdbiVopwwECaGecsopmhwhUT8xch3+N5lK4Bz/ucak4xtSRbg+qJzUg1yGFdxjjz3UhRdeaEXNhVitaIbyUqJ9+/aaWAkE5xd2XrVu3dp/eN1/iJIRLKTqFXbeGAIl+CDpjPDfP6I15+Q7PQiwQeCf//ynFRUSYrWiGcpHCVy7QYx33313hUpDfpwzI88KCZTShOqfGiAdI1SmBBDyeeihh9Zdbgh33QH5kUoETj75ZO3H14bKCbHa0AplpMPxxx+vGjRoEFhjRpbswGK02bdvX3Xrrbfqb+/oEwINCsMBkXoJl/8QKqNfGa0Gwp26g23btg3sG6WoqBBrKVAv0zIfe+wxTX4vvPBCIAJm1Ml0AKTIf35750/NMX8GLFZ5idV/Xv6nH4GbbropdB8wpn70Ge+Hh3scIsQaB4qSR04E1qxZozcCnHXWWRnTQpp0cv8I0zvvKsSaEb6yP9G/f3/dfxYvXpwTC/oR8/I8kL0f79tRzkyyJBBizQKOnIoPga5du+pOP2fOnIyZZiJNjpv5U0YUjGD9wnEZsfpRKa//Tz/9tO4DkydPzllx81aUM2GeCYRY8wROLguPwCeffKLDrRx99NGK8BkECwwS5kUxmfGLl3DNApd/ZMFcKjeLSPki8Pbbb2tihWBzCQ9h7wJnrvRRzwuxRkVM0kdGAGN/CPO3335TdPrevXurIFMryNLYp3oL8U4FcJwFLu9cGNeRv/eY93r5XR4IzJ07VxNrrn5gHs7+Kac4URJijRNNyasCAuzdZnQwZMiQdedee+017c3qu+++W3fM/DCr++yswiqAqALGUsCkMQsPEDZpIFXmy/yjWJNevssDATxbbbvttqpjx45ZK2z6GH3L+8l6UcSTQqwRAZPk0RA48sgjVZMmTSpcBLlmGlmwmGBMpUgTRJgmDTu0MqWpUKgcSD0CeEpr0aJF1nrSt3hYM8Xk/WS9KOJJIdaIgEny8AgMHDhQj1bHjRsXeBHzrWHmwwIvloOCQAACjEAbNmwYcObPQ7zdQKhJihBrkuiWcd6MMgljjdF2Jlm7dq26/fbbVTZLgUzXynFBIAgBRqu77bZb0Kl1x5ia8m+JXncyph9CrDEBKdmsj0Dnzp1VlSpV1JIlS9Y/4fs3depU1a9fP99R+SsI5IdAhw4dsoZoYQoJYs22bTq/kte/Soh1fTzkXwwITJ8+XXfe7t27h8qtZ8+eavbs2aHSSiJBIBsC3bp1031vxYoVgcmYjw/aEh2YuICDQqwFgJfWS3mqs9ru/UR5wp9++unqgAMOCA3P+PHjFaE1RASBQhF48MEHNbFmml6iHydpZmX0F2I1SMj3OgRYaTcT/Kyg8jusQfWIESN02iiLUowumDoQEQQKRQA/FPTVsWPHFppVQdcLsRYEXzovNqYo3tpBsGHmpurVq6eaN2/uvTTUbyIKLFiwIFRaSSQIZELgvffeCz0IyJRHHMeFWONAMUV5sJoPgTId4BVzPMhMhTnSxo0bq7p16+prmWONKphe4atVRBAoBAHmUCtVqqRq1aqlt08Xklch1wqxFoJeCq81u5qCqubfWkoadkhBxN4Pgd2iypgxY9To0aOjXibpBYF1CAwePHi9fkifHDZs2LrzxfwhxFpMtB0oixEpc6pBEuQRaIMNNqjQmZlK8G4VDPOb0W7t2rUjXxcmb0mz/tbNtOLBar/3Ac/vZs2aBXXlxI8JsSYOsVsFBI1KTQ3oqP6pAF67/J0ZA+203rxSL3tJumrVqhX64jHHHGO6b1G/hViLCrf9hfHUD3KnZqYI/KYq7KzyE+uUKVPsr6homDoE2Gji74sPPPBASeopxFoS2O0sNJs7NaYHMk0R3HDDDfrccccdp0aNGmVn5USrskCAIJWHHXaYOvzww9WgQYNKVmch1pJBb1/Bxp2aVzOsATCfYiTrH61608lvQUAQ+BMBIdY/sSj7X9iq4tvU7LhixZ8wKIxUhVTLvnsIABEQEGKNAFbak0KsLF6ZD/+T9gKUdkylfuWJgBBreba71NoCBHhw8QkSHm5+C4RMaYOul2OlRUCItbT4S+lliADz1kSdZd4aAg0SVrcJkIh5m/kEWWsEXSvHSo+AEGvp20A0KCME8K7EvDWjTwgzG7HKvLa7HUOI1d22E80dRcD4YchErMbszdHqidpKKSFW6QaCQIkQyESsxss932+99ZZYZJSofQopVoi1EPTkWkGgAAQyEasZseJzAVM35luZPpA51gLALvKlQqxFBlyKEwQMApmI1Zz3fuMOD4I10wjec/LbPgSEWO1rE9GoTBCIQqxAwuiVa0TsR0CI1f42Eg1TikBUYsWCQIjVjc4gxOpGO4mWKUQgCrFipsVUgOyEc6MjCLG60U6iZQoRyESszKfip2HkyJHaKgDfDfhwIMijiBsICLG60U6iZQoRYJU/aJsqVgHsuuLVnw+EKhYBbnUAIVa32ku0FQQEAQcQEGJ1oJFERUFAEHALASFWt9pLtBUEBAEHEBBidaCRREVBQBBwCwEhVrfaS7QVBAQBBxAQYnWgkURFQUAQcAsBIVa32ku0FQQEAQcQEGJ1oJFERUFAEHALASFWt9pLtBUEBAEHEBBidaCRREVBQBBwCwEhVrfaS7QVBAQBBxD4P4MdO+OuaE1QAAAAAElFTkSuQmCC[/img][br][br]Find the length of [math]EF[/math].
Find the measure of angle [math]E[/math].[br]
Find the measure of angle [math]F[/math].[br]
Decide whether triangles [math]ABC[/math] and [math]DEC[/math] are similar in the applet below. Explain or show your reasoning.
What is the length of segment [math]DF[/math]?[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAhgAAAE/CAYAAAAExboDAAAgAElEQVR4Ae2dCdxM1f/H/7IkkeyFLCGyZxeyhChlSxKyK0q2LJUQ/SyVrGWpbGUvZF9SZI0KIUpIieRHQoulvv/X5/x+5/ndZ56ZeWbmuTNz7r2f83rNa2buPfcs73OXzz3ne77n/4SBBEiABEiABEiABGwm8H82p8fkSIAESIAESIAESEAoMHgSkAAJkAAJkAAJ2E6AAsN2pEyQBEiABEiABEiAAoPnAAmQAAmQAAmQgO0EKDBsR8oESYAESIAESIAEKDB4DpAACZAACZAACdhOgALDdqRMkARIgARIgARIgAKD5wAJkAAJkAAJkIDtBCgwbEfKBEmABEiABEiABCgweA6QAAmQAAmQAAnYToACw3akTJAESIAESIAESIACg+cACRhKoGfPnlKrVq0kn927dxtaYhaLBEiABP5HgALjfyz4iwSMIpA/f36pWbOmDBkyJNHn119/NaqcLAwJkAAJ+CNAgeGPCreRQJwJQET83//9n3zyySdxLgmzJwESIIHICFBgRMaNR5FAVAksWbJECQz2VkQVMxMnARKIIgEKjCjCZdIkECkBDItgiISBBEiABJxKgALDqS3HcruaAGwvbr755kQGno0bN3Z1nVk5EiABdxGgwHBXe7I2LiGQOXPmJAaeM2bMcEntWA0SIAEvEKDA8EIrs46OInDs2DEaeDqqxVhYEiABfwQoMPxR4TYSiCMB9FRgBgkDCZAACTiZAO9iYbbe2LFjZejQoQmfcePGCS39w4TI6EEJwMFWmTJlgsbhThIgARIwnQAFRpgthDdL3PxhhIcPLP1hjEfvimGCZPSABHBetWvXLuB+7iABEiABJxCgwAijleD0CAIDY+Q6oPcCIgNvnQwkYAcBnGP+PnakzTRIgARIIFYEKDDCIA3fBLDu9w144+QUQl8q/B8pAQhZ3w97yCKlyeNIgATiRYACIwzyEBEQE9aAGz/eNjmF0EqFv0mABEiABLxOgAIjjDMAQyFY3VIbebZv3171aKBng4EESIAESIAESOB/BCgw/sci6C+9+JTVwBPDJRAZnEUSFB13Wgi88847Urx4cUmXLp00atRIDh48aNnLnyRAAiTgHgIUGCG2pb/Fp7SBJy3+Q4To8WibNm1KYrxZrlw5j1Nh9UmABNxKgAIjxJYNtPgUtsMGg4EEkiPQr1+/JAID586XX36Z3KHcTwIkQAKOI8AnY4hNFmimiD/DzxCTZDSPERg0aJBfgXHgwAGPkWB1SYAEvECAAiPEVoa9Bbx4WgP+cwaJlQh/ByOwd+/eJAID59X+/fuDHcZ9JEACJOBIAhQYITSbXnwKYsL6wawSTk8NASCjJBDADCScQ4UKFVK+U/LlyyeFCxeWzZs3J8ThDxIgARJwAwEKjBBaEcacdHwUAihGSZZA9+7dJXfu3AnxduzYIXfddZdky5ZNli1blrCdP0iABEjA6QQoMJzegiy/YwgcP35c7rjjDhk2bFiiMh86dEhq164t1113ncyaNSvRPv4hARIgAacSoMBwasux3I4jAB8YGB45c+ZMkrL//PPP0rRpU7UfK/QykAAJkIDTCVBgiMjHH38sXbp0kTZt2sjChQud3qYsv6EEWrVqJeXLlw9Yur/++ks6dOigRMbgwYMDxuMOEiABEnACAc8LjOXLl6sbutV4c8yYMU5oO5bRQQT27NkjOXLkkLfffjvZUvfu3Vudkz169Eg2LiOQAAmQgKkEPC8wHnzwwSQCo2DBgqa2F8vlUAKvvfaaOs9CLT7sNCB60at29erVUA9jPBIgARIwhoDnBQa6rK29F/iNdSIYSMBOAg0aNBCI2XDChAkT1Ln5wAMPyOnTp8M5lHFJgARIIO4EPC8w/HlXbN68edwbhgVwDwFMcU6TJo2sXLky7ErNnj1bbrzxRrn77rsFs00YSIAESMApBDwvMNBQDRs2TNSLcfToUae0H8vpAAIvvPCCOr8iLSr8Y+TJk0fuvPNO2b59e6TJ8DgSIAESiCkBCgwRgfOj7Nmzy4kTJ6RIkSIycODAmDYCM3MvgQsXLkjlypWla9euKaokPH2WKFFCcuXKJatWrUpRWjyYBEiABGJBgAJDRDJkyCCdOnVSvN977z31tnnp0qVY8GceLiewePFidT7t3r07xTXdt2+fVK9eXdkIzZkzJ8XpMQESIAESiCYBzwuMkydPqgfA0qVLEzijK7pv374J//mDBCIlgN4x9DrYFX788Udp1KiROmcnTZpkV7JMhwRIgARsJ+B5gfGvf/1LUqVKJf/8808C3Pnz56sbONYgYSCBSAlo1+BY4MzOcPHiRTV9FTOehg8fbmfSTIsESIAEbCPgeYGBlSwfeuihJEBLliwpPXv2TLKdG0ggVALaNXi0ppg+/fTTSgjDMRcDCZAACZhGwPMCA2+Bb731VpJ2WbRokbp5+1s3IklkbiABPwTgGhwrpUYz6GnW7du3j2Y2TJsESIAEwibgaYExc+ZMJSJOnTrlF1zZsmXVDBO/O7mRBIIQ0K7Bp02bFiSWPbvg2h5CuXHjxnLu3Dl7EmUqJEACJJBCAp4WGDVr1pQqVaoERLhkyRJ144YhKAMJhEMgXNfg4aTtLy6GY+CB9p577pEjR474i8JtJEACJBBTAp4WGHjrg5FnsFChQoUU+zAIlj73uZMAXIPDxXcswwcffCA5c+aUUqVKya5du2KZNfMiARIggSQEPCsw1q9fr3onvvrqqyRQrBv0aqs//PCDdTN/k0BAAnANnjp1asG5E+uwYcMGueOOOyRv3ryybt26WGfP/EiABEgggYBnBcZjjz0mhQoVSgAR7AeGUTp06BAsCveRQAKBlLoGT0gowh9ffvmlVKpUSa1hsmDBgghT4WEkQAIkkDICnhUYGB7p1atXSPRWr16tejs4th0SLk9H0q7BO3fuHFcOWE/nvvvuU+ftlClT4loWZk4CJOBNAp4UGF9//bW68aI7OdQAF81t27YNNTrjeZSAdg3+xRdfxJ0AHMW1bNlSnesjR46Me3lYABIgAW8R8KTA6Nevn2TKlCmsltY2G998801YxzGytwjANXiOHDmMqvQTTzyhREb//v2NKhcLQwIk4G4CnhQYeADABiOU8Ntvv8nGjRtl1KhRcvvtt8ujjz4aymGM40EC2jX44MGDjav9gAEDlMiI99CNcWBYIBIggagR8JzAOH/+vLrRtmjRQmbPni3omUB39sGDB+XQoUOyd+9e2bRpk8A4bvTo0QI3zDNmzJD9+/cLZgfAdgO/GUjAl4B2DW6q3xQMk+D8bd68ucBWhIEESIAEoknAcwJj3Lhx6ib73XffyebNmwUuweFtcfz48YJ9kydPlrlz5wrsMw4fPpyEfd26deXhhx9Osp0bSACuwcuUKWM0CBh8YnG/OnXqCHpcGEiABEggWgQ8JzDg/rtevXoR84QowVsgXEEzkIAmoF2DQ6CaHrBacJYsWdQ6KTyPTW8tlo8EnEvAcwID4mDChAkpajF4acS6DwwkoAnE2jW4zjfS7zVr1kjBggWlQIEC8vHHH0eaDI8jARIggYAEPCUw9Aqp33//fUAgoezYvn276sWgO+ZQaHkjDkQnPk4KO3bsUL0YmTNnFrgZZyABEiABOwl4SmBgbQi7xsgbNWoU87Um7Gx4pmUfAe0a/MMPP7Qv0RilhGnXtWvXVoL57bffjlGuzIYESMALBDwlMDA8MmjQIFvaFb0XSA+9GQzeJhBv1+AppX/mzBlp1qyZOp9fffXVlCbH40mABEhAEfCMwNi2bZu6gX722We2NX2TJk2kfv36tqXHhJxHQLsG79ixo/MK71Ni1AGi+fnnn/fZw78kQAIkED4BzwiMrl27Su7cucMnFOQILCqFG/Knn34aJBZ3uZmAdg3uFnucPn36qHO6W7dubm421o0ESCAGBDwjMNKmTStwmWx3gNMi+BRg8CYBuAbPli2bqyo/bNgwJTLgtfbPP/90Vd1YGRIggdgR8ITAwKwR9DSsWLHCdrLw/Im0OdXPdrTGJ6hdg9tl12NShTGVG+c1hgB/+uknk4rGspAACTiEgCcExtChQwU9GNEKWLGyRo0a0Uqe6RpKQLsGP3HihKElTFmx3n33XcmYMaNUrFiR7vFThpJHk4AnCXhCYMCZUNOmTRM1MJayhpFmz549E233/YN1SGrVqiW7d+9OtAvbIVyOHTumbr5421u7dm2iOPzjbgJwDV6qVClXV3L58uWSN29eKVy4sHKt7+rKsnIkQAK2EnC9wLh8+bLq6p0+fXoicO3atRM4GKpZs2ai7dY/EBX58+dXx8PXgQ5DhgxRC5/h/9ixY9Xv1q1bS9WqVXUUfrucAFxsZ8+eXd544w2X11SUsChZsqSyNVm2bJnr68sKkgAJ2EPA9QLjrbfeUgLBunrkkiVLlHBA70UwgQGnXBAQ6J2wCgzfXg/8x2qsiLdy5Up7WoapGE1Auwb/559/jC6nXYXbt2+fVK9eXa677jqZOXOmXckyHRIgARcTcL3AqFatmrox6jbE0MjNN9+sBAN6MQIJDPRSYB96MUIRGEgf6VWoUEFnxW8XE4BbcK/5QMEy9PBgi+sBwpuBBEiABIIRcL3AwM1w9OjRCQwgGnQPBH77ExjorcDwCewr8NtXYMD+AjfYjRs3KlGh7TOwvDviLl26NCE//nAfAZwTeJNHT5jXwpUrV6Rt27bqPB88eLDXqs/6kgAJhEHA1QJj1apV6kb47bffKiQQBRj2QC8Ggj+BgX0wCoWIQPAnMLBdiw+dloosIp06dRIsCc/gXgJOdw1uR8v06NFDXVv4ZiABEiABfwRcLTAeeeQRKVq0qKo3ehkwNKJ7G7DRn8DAMuzWpdgDCQx/MLHt6NGj6sb7/vvvB4rC7Q4moF2Dt2/f3sG1sKfoL774ojrX27RpI9euXbMnUaZCAiTgGgKuFhgYrujbt69qLPRcwK7CGnwFBrq8MTRi7ZUIV2AgfXgMLVGihDUr/nYJAe0aHEudM4iMGTNGiQysVPzLL78QCQmQAAkkEHCtwMA0QggMrBOiZ4LAn4X1gx4NfLANQyIQFxgescbBcAfSwTe2hxLg4RHHzJs3L5TojOMgAnANniVLFgeVOPpFhcOxdOnSqWnahw4din6GzIEESMARBFwrMHr37p3wIEAvBHovfD/wcYEPtgeKg5khEAv49u0BCdbCTz31VMLwTLB43OccAnA5X6RIEXnuueecU+gYlRQ9O7ly5ZJixYrJ9u3bY5QrsyEBEjCZgGsFBnomHn/88aDsfYdI/EWOZIgE6cB9NIQJ3C0zuIPA22+/rdr0hx9+cEeFbK4F1uOBzROEBgysGUiABLxNwJUC4/Tp0+pBsGjRoqCtG02BgYwxHfb2228PWgbudA4BrC5avHhx5xQ4DiX98ssvpXLlymrIZM6cOXEoAbMkARIwhYArBYb2spgcZMwosc4q8RcfBp/oxbAafvqL52/bqVOnlNDxdVPuLy63mU0A5wmWZZ84caLZBTWgdOjhue+++9S5T14GNAiLQAJxIuBKgYEZHA0bNowT0sTZYhZLvnz5Em/kP8cRePXVV9UDk9MxQ2u6P/74Q7DKMIYJhw0bFtpBjEUCJOAqAq4UGLipmbIIFabuoTzTpk1z1Ynjtcrgjbxu3bpeq3aK6/vkk0+q8x9G1wwkQALeIuA6gTF37lx1Qzt79qwxLTlgwAC59dZbjSkPCxIeARgvwjX4Bx98EN6BjK0IDBw4UF2TdE7GE4IEvEXAdQIDC1CVL1/eqFaE2DGpV8UoOA4ozPPPP6/azwFFNbaIo0aNUgzhJTcSeyZjK8aCkQAJBCTgOoGBB/nQoUMDVjheO/CQypEjR7yyZ74REvjtt9+kUqVKyU55jjB5Tx02ZcoUSZUqldxzzz1y5MgRT9WdlSUBLxJwlcDQPisOHDhgXFviQQXxM378eOPKxgIFJoBhEbTbtm3bAkfinpAJzJ8/XznAK1WqlOzatSvk4xiRBEjAeQRcJTA6dOhg9IwNLG8NB2AMziHQrVs35ULeOSU2v6Rr165V/mHy5Mkj69atM7/ALCEJkEBEBFwlMPCmibUiTA2XLl2S1KlTC/x0MJhPQLsGh5Eug70Edu7cKeXKlZMMGTLIggUL7E2cqZEACRhBwDUC45tvvlFd2Rs2bDACbKBCwCdAxowZA+3mdoMIaNfgEBoM9hM4evSo1KlTR123sM9gIAEScBcB1wiMQYMGSfr06Y1vnT///FOuv/56gVU9g9kE4Boci3cxRI8AbJOaNWumRMaIESOilxFTJgESiDkB1wgMjOe2aNEi5gAjyRA3UogMBnMJaNfgNMqNTRt17NhRiYx+/frFJkPmQgIkEHUCrhAYFy5cUDcnpyyudOXKFbnxxhtl+PDhUW9gZhAZAe0a/PLly5ElwKPCJgC3+rCj6ty5c9jH8gASIAHzCMRUYLRr107dQPxhwBtjkyZN1H7cZPAJ1Z/Fm2++GTBdf3mZsO2VV15RBp8mlIVlSEoArsFhH8AQWwIQ3bj2mzdvLhcvXoxt5syNBEjAVgIxERjHjh2TsmXLqul+uHn4C5kzZ5YhQ4YI4iLMmDFDxce25AIcIdWqVSu5aEbt//vvv0Oun1EF90Bh4BocDqEWLlzogdqaV0WswIr7BAQeVmZlIAEScCYB/097m+uSP39+Qe+FdoQVavI9e/aUmjVrJhsdN6MxY8YkG8+0CCgzys4VOs1qGboGj397vPvuu2q21V133SV79uyJf4FYAhIggbAJxERgYPgDIVyBgd6LMmXKBK3UkiVL1EP61KlTQeOZujNbtmyCBxqDGQS0a/DWrVubUSAPl2L58uWSN29eKVCggKBXiYEESMBZBGIiMDSScAUGxAV6PoKFpk2bSvHixYNFMXrfuHHjlED666+/jC6nVwqnXYNv2bLFK1U2up5bt24VuBW/6aabuJqt0S3FwpFAUgLGCgxtg6FtMpIW/T9bMMTgdE+LuXLlkv79+weqIrfHkABcg2fKlCmGOTKr5AjAiV6NGjWUEIfzMwYSIAFnEDBSYGBIBWt2QGQEC5999pm66eghmGBxTd6njdpoNR/fVoLHzsKFCwt9McS3HfzlfvbsWXnwwQfV9Y4pxAwkQALmEzBOYIQqLoD26aefds0S6HAU1rt3b/PPGBeXULsGhwtrBjMJtG3bVokM2i2Z2T4sFQlYCRglMMIRF6gE1vSAB0A3BO3L49dff3VDdRxZB7gGv+OOOxxZdi8VukePHkpkPPnkk16qNutKAo4jYIzACFdcYH487C9Wr17tOOiBCozpvLh5MsSeAM6/rFmzytixY2OfOXMMm8DgwYPV9d+yZUuhgXTY+HgACcSEgBECA4acsLlo3769bNy4McnHn6En1vOAwHBTmDp1qqrTL7/84qZqOaIu2jU4FqNjcAaB119/XV0v9evXl5MnTzqj0CwlCXiIQEyf0IGmqertEAz+Pv68eaIru1GjRq5rqttvv13Y9Rv7ZoVrcKd5g409JfNynD59ulo4sGLFinLgwAHzCsgSkYCHCcRUYNjF+erVq0qIJDfLxK78YpmONjTkG1nsqGvX4PPnz49dpszJNgKLFy8WTPXGDKDNmzfbli4TIgESSBkBRwoMCAv0dLh1pUv0znBFyZSd2OEcTdfg4dAyM+6mTZukaNGiAs+4H374oZmFZKlIwGMEHCkwateuLZUrV3ZtU82cOVMJqOPHj7u2jqZUDK7B0b3eqlUrU4rEckRIAEMkVapUUQvV4RpiIAESiC8BRwoM9F6MHDkyvuSinDvcnyfnJj3KRfBE8to1+KeffuqJ+rq9kqdPn5YGDRoogc4ZQW5vbdbPdAKOExhr1671xNs9VpOEkDpy5Ijp55CjywfX4BkyZHB0HVj4xAT+/vtvgU8TXD+YzspAAiQQHwKOExht2rSRggULxodWjHMtXbq0cFXP6EHXrsH79u0bvUyYctwIYDYWRAZ9y8StCZixxwk4TmDghtGzZ09PNNvcuXPVDfLQoUOeqG+sK6ln7Bw+fDjWWTO/GBEYOHCguoYg1NGzwUACJBA7Ao4SGF999ZW6WWCRM6+EcuXKCbwVMthPAN3omNrI4G4Co0ePVveN+++/X86cOePuyrJ2JGAQAUcJDCxpjvVHvBQWLFigbo779+/3UrWjXlftGnzMmDFRz4sZxJ8AvORed911UrVqVcHy7wwkQALRJ+AogQFnOl6cTlipUiVp1qxZ9M8GD+WgXYP//vvvHqq1t6sKsY71ZooVKyY7duzwNgzWngRiQMAxAgNdm7C/8KITnffff1/VHW/dDPYQwPoV99xzjz2JMRXHENiwYYPAHT9eVlatWuWYcrOgJOBEAo4RGJjTDoHh1XD33XfLQw895NXq21pvuAbHuQQjWgbvEdizZ4/AtildunTy3nvveQ8Aa0wCMSLgmCc2bgj33ntvjLCYl82SJUvUQ3HXrl3mFc5hJaJrcIc1WBSKe+LECXU/gdCcOHFiFHJgkiRAAo4RGLgRwFDLywFd+g0bNvQyghTXXbsG58ycFKN0fAJ//fWXNG/eXAn3YcOGOb4+rAAJmEbAEQJDz6S4dOmSafxiWp5ly5apm+G2bdtimq+bMtOuwTdu3OimarEuKSDQqVMndV317t07BanwUBIgAV8CjhAYDz74oMCrJYNInTp1pF69ekQRIQG4Bk+fPn2ER/MwtxKAN1f0krZv396tVWS9SCDmBBwhMHDhswvzP+fGypUr1Y2Qi3OFf63ANXihQoWEb6rhs/PCEcOHD1fXVuPGjeX8+fNeqDLrSAJRJWC8wMCDFALju+++iyoIJyWOHoxatWo5qchGlFW7BqejJSOaw8hCTJo0Sd1vatSoIUePHjWyjCwUCTiFgPECo2vXrnLLLbc4hWdMyqlXlMWcfobQCcA1OHwgMJBAMAKYupopUyYpWbKkfP7558Gich8JkEAQAsYLjOuvv166d+8epAre3NWgQQOpXr26NysfQa3hpCxLlizyyiuvRHA0D/EagTVr1shtt90mefLkkfXr13ut+qwvCdhCwGiBgVUuMTyyZcsWWyrrpkQ++ugjxQa9GQzJE9CuwS9evJh8ZMYgARHVe1GqVCnJkCGDYCYbAwmQQHgEjBYYQ4YMkdSpU4dXIw/FfuCBB6Ry5coeqnHkVYVr8GrVqkWeAI/0JAEYBsMeAy86kydP9iQDVpoEIiVgtMDAeDkX+QrctJ988om68a1YsSJwJO4R7RqcbqF5MkRCAP534KYfImPEiBGRJMFjSMCTBIwVGFjlEhc0FvpiCEwAU+rKly8fOAL3CF2D8ySwg8Djjz+u7kn9+vWzIzmmQQKuJ2CswIBbcAgMhuAE9DTepUuXBo/o0b1wDV6hQgVp0aKFRwmw2nYSeOaZZ9R9qXPnznYmy7RIwJUEjH2CY9wTK4gyJE8Aw0j0dOqfk3YNjmESBhKwg8DgwYOVyMA6Jl5fvsAOnkzDvQSMFRjovYDTG4bkCWzdulXd8BYtWpR8ZI/FgGtwLMvNQAJ2Enj99dfVNQfX/T/++KOdSTMtEnANASMFhl7U69y5cyGDPnbsmPz6668B4wfbF/AgB+3AEEDx4sUdVOLoFxUzAGAo3LNnz+hnxhw8R2DmzJlqXZuyZcvK3r17PVd/VpgEkiNgpMB45JFHpEiRIsmVXeA8qUmTJupNAj0e+GBmhTW0a9cu0X642MZxOkB4YDqs/jhViOzYsUPVc968ebpqKf4GS/DFDbRAgQLKPfm4ceNSnG6sEtCuwQ8ePBirLJmPxwhgBhc8DefPnz/JvcdjKFhdEkhCwEiBAaEwaNCgJIW1boBIuPnmmwWzKHwFg46HN9fMmTMn7Id4QHw8MHVAHC0qtNjQ+5z2DVfYoQizUOqlhRm+x44dK0uWLFE9ARBiTgktW7ZUwsgp5WU5nUkA4r5YsWJy0003yeLFi51ZCZaaBKJAwDiBsWvXLvUm/vXXXwetLt4Ykuv6rlmzpuqZsCakfUdoUeGbhu9/67Gm/9bsZs+enaKigoFVmKUosTgdDNEJ1+CjRo2KUwmYrZcIYDHGKlWqqHsXes4YSIAERIwTGHi4oWciWMDDA70csLsIFtBbgTdwa5gxY4Z6eOptyE+LDXw7WWCgTq1bt5aCBQvq6oX9rdmCk5ODdg2OaaoMJBALArh/YI0g3Ju45k0siDMP0wkYJzCyZs0qyc0xRzc9ejAQ8CAcOnSowOBKCwUNHQ9LvIn36tVL7UNciBfrwxPHQIQgDavY0Gk47VsLhOnTp0dUdLDQbCNKwJCDsKR91apVDSkNi+ElAq1atVIi47nnnvNStVlXEkhCwCiBceLECXVhJuezAAKjTJkyypYCvRQQBvgP8YAHrDVgSATb8VaBD2wJ3B7gcTBv3rwRVROCzOm9ONo1eEqHiiICyINIQEQwPRr3myeffJI8SMCzBIwSGKNHj1YXZXKtgbdsf2IBYgOzRHSA2MDsB2yHsIBNhm8Pho7rpu+vvvpK8YE31HACenP8cQ0nDRPi0jW4Ca3AMqAHA9cTjI0vX75MICTgOQJGCQwsjdyoUaNkGwE9GBALvgEiAhe0Dv4MQTE8gjjJ2W/oNJz63aFDBzV9LpzyawNYfDs1nD9/XrkGh5dFBhKINwH90oTVfE+dOhXv4jB/Eogpgf89jWOabdLM/vnnH/Xgx6qFcO98+vTppJH+uwUCwzrVVEfUD0j817/9CQkID6Th5nDgwAHF84033gi5mmDl9B4MLI6HOqxfvz7kejMiCUSTAGaVXHfddVKxYkVJbnZcNMvBtEkg1gSMERgYL8eD4eeffxYs3NW7d2+B06gLFy4kYaIfhL72FtoWAwcEioN9sDOwGnomycAlG7p06SLZsmULqzZgA+daTg0Y806TJo1Ti89yu5QAeldxLRYqVEi2bNni0lqyWiSQmIAxArd17rYAACAASURBVANdiFj1Uoc///xTOa3p27evwJGNb4CYQC8GxAiEBjxMwr7CasSJYRQdB8cjHh6eeIj6zjjxTd8N/w8dOqREWzjeN+FUC0IPs2o0I4g1XzFnIh+UE67Bn376aROLxzJ5nMDmzZuVwMBMOSyHwEACbidgjMDAQw0LCPmGw4cPy/Dhw9Wwie8+iAyIBRyLWSRWcYG4egoqhkQQB3FhIIoHkVcC3uhR73ACho/Ay/qBoazp4a233lJlxvAQAwmYSABu68uXLy+pUqVSU+tNLCPLRAJ2ETBCYGC8HA8zDI/4C3/99Ze8+eabwmmH/ugE3waBBravvfZa8Ih+9qLXArYsThFksNbPly+fn5pwEwmYQ+DMmTNy7733qusSPYYMJOBWAkYIDPQqhOK3AdMu7VzMy62N6luvp556SjJkyOC72VX/v/zySzVENmLECFfVi5VxLwHMdIL4f/HFF91bSdbM0wSMEBiwsO7fv39IDTFmzBhZt25dSHEZ6T8Ejh49qm5kI0eOdC0SuGbGzVrbjbi2oqyYqwjAazHOW9oNuapZWZn/Eoi7wNi/f7+6wPbs2RNSo/zyyy/Sp08fQdc/Q+gEnnnmGUmdOrU8+OCD8uyzzzpm2CPUGsI1eOXKlUONzngkYAwBXI8QGVhHCNP1GUjALQTiLjDg7e76668Pi+e2bdu4mFBYxEQaNmyobmK4keGDIal///vfYaZiZvQNGzaoOmE9GgYScCKBl19+WZ3D999/v2uuSye2A8tsL4G4C4zbbrtNsHZGuGHixImCaV8MwQnAsyWmxGlhYf12i4GZdskcnAT3koDZBCZPnqyuUyzS9+2335pdWJaOBEIgEFeBce7cOXVBrVmzJoSiJo7yzTffyEsvvZR4owf+wT8IFoX74osvZMWKFTJt2jTFAdNR4QUV3gLz5MmjPAdaxYS/325Y7RECCtP+mjZt6oHWZxXdTmDRokWSKVMmKVasmHz22Wdury7r53ICcRUYEyZMUAIjUsaYeomFvZwcrl27ptyiw4UwemRwgxk/frwMHDhQ9ezAtqBEiRIC5zz+RAK2pU+fXtAThAdtgwYN1HFwUIZ1ELBsO3owsmTJkuT4jz76yMnoVNm1a/C1a9c6vi6sAAmAAKaGY7p1rly5ZPXq1YRCAo4lYLvAwMUBL5ChhEqVKgk8eEYaNm7caKSzGvTMwAgVHkhXrlwps2bNklGjRgkMLVu0aCHVq1dXHidvuOGGJA99LSLglbRIkSJSrVo15X20a9eu8sILLyjxMXfuXIE42Lt3b0DfIb5MUQ6kh/QxZdUt0znRc4NZSAwk4CYC+/btk9KlS0vatGllzpw5bqoa6+IhArYLDO01MxTnTHjYpcQw7+zZsyFPb01Jm168eFG+//57NSyBKbLwxTFp0iS1YBrW+8AKsOXKlZNbb701oGDAQxBvJFgxtk6dOvLoo49Kjx49lJfSKVOmKLfoW7dulSNHjsjvv/+ekuIGPRbC5++//w4axyk7cY4VLFhQunfv7pQis5wkEDIBrL56zz33qHsKbM4YSMBpBGwVGDAa1AIDPRnBAoYCIDCuXLkSLFqy++DW+uTJk8nGs0aAHcNPP/2khldQTnSzw4kX3uoxtNCmTRslAu68807lvEn3Kvh+oycA9YXdA6y/27dvL/369ZNXX31VeR2FGMEQDqbWMthPQLsGx9seAwm4kcDVq1eVbRXuPcOGDXNjFVknFxOwTWDAwRG69bFKKS6GQKuV4u0Z4gJv/MWLF08xWhg57ty5M5EdAxZAe+edd9RU1gEDBgic2cAIENbZBQoUkHTp0gXsaYCtQ9GiRaVGjRrSrFkzQRf84MGDBRbeWOtk+/btyocERApDfAk88sgjyqA1vqVg7iQQfQKYaYf7aq9evaKfGXMgAZsI2CYw0JOAt3kErGKK/74B3fOFCxdOeLhjfDHQDBJfOwasQ4IekkGDBkm3bt0EDxf480cXuT8DRt3bgKW7MXSBxdDq1q2rnNmglwIGou+9956yZYCzL7f4hPBlHq//aCusZKvboVatWolWZEXPkd7n79vf+WOti3YNDv8BDCTgBQJY3BHXCpZWYCABJxCwRWBgLFz3XqDSEBj+LoKOHTsmeajA4ROMH+HFDjMgMNyAJbcxVcvfgwfbMmbMqIRFlSpVlAEkehkwZRXDHB9++KGa3nX8+HG5fPmyE9rAdWXUQ2XoxULPFhZNw2qsOEe0K298Q2T4ftBLhDYO1AOmYWnX4BSGmgi/vUAAwhvXB6ak//bbb16oMuvoYAK2CAyICfQQ6AClDZHhGzDdMpBoyJEjhzKAxLTMtm3bKuNNLN+OGRMff/yxYBqnfjj5psv/5hHwbSv8D0U4WHvCgtUKvVEQowwk4DUCMPjEtYRh3FCM6b3Gh/U1h0CKBQZOcJzsTZo0UdNTMUUV3eGwdfANHTp0SCIwMFWVwRsEcJ6gdyNYwDBbcsMj2jU47GwYSMCLBDCTDf5vSpYsqWa3eZEB62w+gRQLDPRU4KGAb/1BbwYeJr4B3jdhM4F9+OACWbVqlW80o/+jux/+N/jmEF4zgRvaPBg3DItkzpw52Z4qugYPjz1ju5PA+vXr5ZZbblGGzm5wmufOVvJ2rZKqgDB4aEM9fFuD3u7vYYJpqVDf8DCJed5OCXhAolcGD0k8BPEdqkMxp9QxmuWE+IQdRrAAoerPdsd6jHYNnlxa1mP4mwTcSgDGzphOjynzCxcudGs1WS+HEkiRwNA9Fr5118MmvsLDN55T/sN+AOLC+vBD3SA0kjNGdEodo1lObaPja5dhzVMbd/oTpdZ42jU4XShbqfC3lwn88MMPago+XnrgtI+BBEwhELHAwIM1WJc39rnl4asffr4PSNgKYComQ2ACEBcQYugBChYgVq0CLlDcJ554Qp13gfZzOwl4kcAff/whDRs2VNeGW5YB8GI7uq3OKRIYwQQEHr5u6cFAXfAA9A16KMh3O///h0Co4kJzTO58Qe8GbHgwLZmBBEggKYFWrVopkQGPwgwkEG8CEQuMeBc8lvlj5gN8OPgG3bOR3IPR9zgv/A9VXIAF7Cn8CThfTto1OBZ5YyABEvBPAI4I0YMMD8YMJBBPAhQYIdDXNiVWo05s054qKTASQ9QeB8eNG6dm3GDWjfVjja3ZBusN0/HhvRVeWRlIgASCE8DKyxAZWO4gmosnBi8F93qdAAVGiGcAHoCwJUBPBoQFZjygZwMXsa9tRohJujYaeiPAJdDHWnH0dIBlcgHW8uDPBZ+SI8X9JPAfAnBUiGuwdu3acuLECWIhgZgToMAIEzl6K3SPBUQHLmCG6BPQrsG5Mm30WTMH9xDAGk6pU6dWL0VY2ZmBBGJJgE/HFNDG2zf9MaQAYBiHwjV4+fLlwziCUUmABEAAzgyzZcumegoxVMlAArEiQIERIWn0YqD3QvdmRJgMDwuBgHYNDiNPBhIggfAJ7Ny5UwoVKiQ33XSTLF68OPwEeAQJRECAAiNEaBAS2lCxV69eyhYDxowM0ScwcOBADkVFHzNzcDmBo0ePSoUKFdS1xHV8XN7YhlSPAiPEhoCY0GuuYGiEPRchgkthNLgGL1eunDRq1CiFKfFwEiCBCxcuCIYb0fv66quvEggJRJUABUZU8TLxlBLQrsFXrlyZ0qR4PAmQwH8JPPzww0pkYOFABhKIFgEKjGiRZbq2EKBrcFswMhESSEIAjrjQk0HPuEnQcINNBCgwbALJZOwnACdcWGSua9eu9ifOFEmABKR///5KZLRs2VKw0jUDCdhJgALDTppMy1YC2jU4nGwxkAAJRIeA9jFTr149+fnnn6OTCVP1JAEKDE82uzMq3aJFC8mVK5czCstSkoCDCUyfPl31ZGCWycGDBx1cExbdJAIUGCa1BsuSQEC7BsdKtgwkQALRJ7Bs2TLlJwP+MrZu3Rr9DJmD6wlQYLi+iZ1ZQd1tyy5bZ7YfS+1MAtu2bZN8+fJJ1qxZZfny5c6sBEttDAEKDGOaggWxErj33nvlrrvusm7ibxIggRgQ+Pbbb6V06dKSKlUqmTVrVgxyZBZuJUCB4daWdXC9tGvwqVOnOrgWLDoJOJfA2bNnRa+KPG7cOOdWhCWPKwEKjLjiZ+b+CNA1uD8q3EYCsSeAxRzhK2Pw4MGxz5w5Op4ABYbjm9BdFdCuwe+//353VYy1IQGHEsDSCBAZTz/9tENrwGLHiwAFRrzIM1+/BLRrcBqY+cXDjSQQFwJ9+vRRIqN169ZxyZ+ZOpMABYYz2821pYbXTrwtMZAACZhFYMSIEeraRO8ibDQYSCA5AryTJ0eI+2NGQLsGxxoJDCRAAuYRmDZtmhIZVatWlcOHD5tXQJbIKAIUGEY1h7cLo12Df/75594GwdqTgMEEPvjgA7nhhhukaNGisnPnToNLyqLFmwAFRrxbgPknEMAS0jly5Ej4zx8kQAJmEti0aZPceuutkjNnTlmzZo2ZhWSp4k6AAiPuTcACgABcg990003y4osvEggJkIADCBw4cEDuvPNOSZs2rcydO9cBJWYRY02AAiPWxJmfXwKjR49WY7snT570u58bSYAEzCNw+vRpgT0GDLMnTZpkXgFZorgSoMCIK35mrgnANXiZMmX0X36TAAk4hMDff/8tmFkCkTF8+HCHlJrFjAUBCoxYUGYeQQlo1+CTJ08OGo87SYAEzCXw2GOPKZHRu3dvcwvJksWUAAVGTHEzM38EBgwYoG5M/vZxGwmQgHMI9OjRQ13L8P7JQAIUGDwH4koArsGxamqDBg3iWg5mTgIkYA+Bl156SYmMhx56SC5cuGBPokzFkQQoMBzZbO4ptHYNvnTpUvdUijUhAY8TeOONN5TIqFGjhnz//fcep+Hd6lNgeLftjag5XYMb0QwsBAnYTmDBggWSJk0aKVmypJqGbnsGTNB4AhQYxjeRewsI1+D58+eXjh07ureSrBkJeJgADLizZ88uuXPnlo8++sjDJLxZdQoMb7a7EbXW6xrQ3bARzcFCkEBUCOzdu1cKFy6s3IsvWrQoKnkwUTMJUGCY2S6eKBVcg2fLls0TdWUlScDLBH766SepUKGCssuYOnWql1F4qu4UGJ5qbnMqC9fgmTJlkhdeeMGcQrEkJEACUSNw+fJlqVu3rhIZI0eOjFo+TNgcAhQY5rSFp0qiXYOfOHHCU/VmZUnA6wRatGihREb//v29jsL19afAcH0Tm1nBOnXqKOtyM0vHUpEACUSTQLdu3ZTI6Ny5czSzYdpxJkCBEecG8GL2sCbHugWYK89AAiTgTQJYORn3gWbNmskff/zhTQgurzUFhssb2MTqadfgWCSJgQRIwLsExo8fr0RG7dq1BYagDO4iQIHhrvY0vja//vqrlC1bVurXr298WVlAEiCB6BOYM2eOEhm4L+zbty/6GTKHmBGgwIgZamYEApgHj27RxYsXEwgJkAAJKAJr166VzJkzK8d7mzZtIhWXEKDAcElDOqUaXbp0UQLDKeVlOUmABGJD4PPPP1cCA9PXlyxZEptMmUtUCVBgRBUvE7cSOHr0qLqBcClnKxX+JgES0ASwMFqZMmXUS8j06dP1Zn47lAAFhkMbzonF1q7Bd+zY4cTis8wkQAIxIHDp0iWpWbOmEhmvvfZaDHJkFtEiQIERLbJMNwmB5s2bS5YsWZJs5wYSIAES8CXQtGlTJTKef/5531387xACFBgOaSinF/OLL75QrsGfe+45p1eF5ScBEogRAW2zBcdcDM4jQIHhvDZzZIlHjRql3kaOHz/uyPKz0CRAAvEhgJcSzDxr2bKlXL16NT6FYK4REaDAiAgbDwqXAFyDFy9ePNzDGJ8ESIAEBLYYEBn16tWT06dPk4hDCFBgOKShnFxM7Rp84sSJTq4Gy04CJBBHAjNnzlQiA8u+Hzp0KI4lYdahEqDACJUU40VMAKsm4u2D3ZsRI+SBJEACIrJixQq54YYbpFChQrJt2zYyMZwABYbhDeT04mnX4HXr1nV6VVh+EiABAwhgmnvu3Lkla9asSnAYUCQWIQABCowAYLjZHgLaNfj7779vT4JMhQRIwPMEvvvuO2XTlSpVKpk9e7bneZgKgALD1JZxSbn0NDOXVIfVIAESMITA+fPn5e6771bDr1iVlcE8AhQY5rWJa0oE1+D58uWTtm3buqZOrAgJkIBZBBo1aqRExpAhQ8wqGEsjFBg8CaJGYOrUqerCpzFW1BAzYRIgARFp3769utf06NGDPAwiQIFhUGO4rShwDY4lmBlIgARIINoEnn32WSUy2rRpE+2smH6IBCgwQgTFaOERgGvwjBkzyoABA8I7kLFJgARIIEIC2mPw/fffL+fOnYswFR5mFwEKDLtIMp1EBEaOHKneJo4dO5ZoO/+QAAmQQDQJvP322+reU6VKFcFsE4b4EaDAiB97V+dcu3ZtKVasmKvryMqRAAmYSWDp0qWSJk0aKVq0qOzatcvMQnqgVBQYHmjkWFdRuwYfN25crLNmfiRAAiSgCGzZskWyZ88uOXPmlLVr15JKHAhQYMQButuz1K7BL1++7Paqsn4kQAIGE8CaJUWKFJG0adPKvHnzDC6pO4tGgeHOdo1breAavEyZMoLVUxlIgARIIN4Ezpw5IxUrVlR2GW+88Ua8i+Op/CkwPNXc0a/swoUL1YWMbwYSIAESMIVAgwYN1L3p5ZdfNqVIri8HBYbrmzi2FezcubO6iGObK3MjARIggeQJwEcGVnbu06dP8pEZI8UEKDBSjJAJaALaNXjr1q31Jn6TAAmQgFEEevXqpUQGvH8yRJcABUZ0+Xoqde0aHNbbDCRAAiRgKgEMk6Ano3HjxnLx4kVTi+n4clFgOL4JzalAs2bNlPdOc0rEkpAACZCAfwJTpkxRIqNGjRpy/Phx/5G4NUUEKDBShI8HawLaNXi/fv30Jn6TAAmQgNEEFi1apERGiRIlZPfu3UaX1YmFo8BwYqsZWGbtGvzIkSMGlo5FIgESIAH/BD755BO1KGPu3Lllw4YN/iNxa0QEKDAiwsaDfAnANfgdd9zhu5n/SYAESMB4Avv27ZP8+fPLDTfcIO+//77x5XVKASkwnNJSBpdTuwZ//fXXDS4li0YCJEACgQmcOnVKypYtq4ZMpk2bFjgi94RMgAIjZFSMGIgA7C5gkf3nn38GisLtJEACJGA8gatXr0rdunXV/QxLvzOkjAAFRsr4ef5o7Rq8Zs2anmdBACRAAu4g8OijjyqRMWDAAHdUKE61oMCIE3i3ZKtdg8+fP98tVWI9SIAESECeeuopJTK6dOlCGhESoMCIEBwP+w+BTp06qYuQPEiABEjAbQSGDBmi7m/NmzfnEHAEjUuBEQE0HvIfAnANftttt0mrVq2IhARIgARcSWDixIlKZGCm3MmTJ11Zx2hVigIjWmQ9kK72hLdp0yYP1JZVJAES8CqBefPmKZGBWSb79+/3Koaw602BETYyHqAJwDV4hgwZ9F9+kwAJkIBrCaxfv17d7/Llyyeffvqpa+tpZ8UoMOyk6aG04Br8xhtvlL59+3qo1qwqCZCAlwnAnTg8fmbKlEmWLl3qZRQh1Z0CIyRMjORLYMSIEarL8PDhw767+J8ESIAEXEvgxx9/FKxdAt8/M2bMcG097agYBYYdFD2YRq1ataRw4cIerDmrTAIk4HUCcCoI3z8QGWPGjPE6joD1p8AIiIY7AhHAWCQurNdeey1QFG4nARIgAdcTwPRV3AtfeOEF19c1kgpSYERCzePHaNfgv//+u8dJsPokQAJeJ/DEE08okdG9e3evo0hSfwqMJEi4IRgBuAYvXbq01KhRI1g07iMBEiABzxBADwZ6MuBi/Nq1a56pd3IVpcBIjhD3JyKwYMECdSHNnTs30Xb+IQESIAEvExg7dqy6N9avX19++eUXL6NIqDsFRgIK/giFAF2Dh0KJcUiABLxI4N1331Uio0KFCvLNN994EUGiOlNgJMLBP8EIaNfgLVu2DBaN+0iABEjAswRWr14tadOmlUKFCsn27ds9ywEVp8DwdPOHV3ntGvyTTz4J70DGJgESIAEPEdi5c6fkyJFDsmTJIitXrvRQzRNXlQIjMQ/+C0KgadOmkj59+iAxuIsESIAESAAE0ONbtGhRNWSCoRMvBgoML7Z6BHX+/PPPlWvwXr16RXA0DyEBEiAB7xG4cOGCVKtWTYmMCRMmeA4ABYbnmjyyCmvX4DRciowfjyIBEvAugcaNGyuRMXToUE9BoMDwVHNHXlm4xb399tsjT4BHkgAJkICHCegZeM8884xnKFBgeKapI6/ounXrlPp+5ZVXIk+ER5IACZCAxwkMGDBA3Uvbtm3rCRIUGJ5o5pRV8tlnn1UXBcYTGUiABEiABCIngBc1eP184IEHBJ6R3RwoMNzcujbUTbsGh6ESAwmQAAmQQMoJTJ8+XYmMqlWrypEjR1KeoKEpUGAY2jCmFEu7BvfqNCtT2oHlIAEScBeBZcuWKZGBqay7du1yV+X+WxsKDFc2q32V6tixo7oI7EuRKZEACZCAcwjs3r1batWqJfgOFnr27Cn4+IYlS5bI0qVL/Q6HbNu2TW6++WbJmTOnwNbNbYECw20tamN90HWXN29eadGihY2pMikSIAEScAYBDBEXKFBAvWQF82CsFzrDbDtraNeuneA4iBP89mdz8e233yq34mnSpJH58+dbD3f8bwoMxzdh9CowefJkdWFt2LAh5ExwMTVp0iThosRFZQ3Hjh2T9u3bS9myZVUcxPW9cBEH88XxwW8GEiABEogHAfRI4B4Go0zf+5QuD+5R6IVAPKvAQHz0Xujg+19vx/e5c+ekfPnyKp8333zTusvRvykwHN180S08XIOnS5cu5ExmzJihLhBclLiwcEFZuxX12wAuQuzDZ8iQIYkuXsTRSt/6O+RCMCIJkAAJ2EAA97DMmTOrXodgAqNMmTLqPoZ7WaQCA8UdM2aMVKpUSd0P//Wvf9lQg+STgDhC3Xw/qJMdgQLDDoouTAOuwTNkyCChOoWBWMBJalXsvlh0HN9uQpzMeuxSCxN9LI6BcGEgARIggVgRwD0KvRL6fhZIYEBU6Iexr8BAWfGyBPsL3MfwO1CYN2+ezJ49W+1+/PHH1b20b9++gaLbth3103VDGfXH+mKYkswoMFJCz8XHQkHjxDt48GBItcTFA3e4wQJOXqTpT2Dg4kTAia0vavz3FRzB0uc+EiABErCDAO5lVkGgH8LWtHGvQg+Hfhj7ExiIj3uY9Z5mTQO/8TI3bNgwuXbtWsKuPn36qHtlhw4dErZF44dVIEUjfQqMaFB1QZro6sufP3/INUFcGDohQEhs3LgxiZDAPqh92F9okYFjcJFabS3QmzFu3Dj10T0bIReEEUmABEggBQRwT8L9TN+jkJSvwMA+GH/qex7iBBIYwYpy5coVef755+Xrr79OEk2v/wSxc+nSpST77diA+7xVSNmRpjUNCgwrDf5WBLRr8FGjRoVMBBcgLjZcdFqcoIvRd3gDFyb2Yx/iQnBYxYXOENv8bdf7+U0CJEACdhPAPQf3JrwkWYOvwMCLj2+PbSQCAz0bc+bMsWaV6Pe0adOUuLnnnnvkhx9+SLTPjj94ubOKJDvStKZBgWGlwd+KgHYNjulToQZcgFD9VlGgjT6t23BB4QKGaobQwHFeW2EwVKaMRwIkEFsCEA24P8HvhfWD+xR6XrU/DOt/HQ8vTPpY3xcrf7XAzJHu3bsn6inxF2/x4sXqPlmyZEnZs2ePvygRbcPQDuqBWX161h6+fcVVRIn/9yAKjJTQc+GxOOlLlSol8C7Xr18/eeutt0JyZYsT1d84I3oooOwRtA2GNR62QUVzKMSFJxOrRAIOIwBhgPuV7wf3N7wUYTtemHz347/uucXvUB7SEA7vv/9+SIQ+/fRTufHGGyV37tzy8ccfh3RMcpH0CyDKbf1om5Lkjg9lPwVGKJQ8FAeOXnAxzZo1S/755x91oWCMcObMmXL27NmAJHCMv4sKJy4uOAS8HeC/b0AXHY5nIAESIAETCQS6v1nLqkWGdVug37i3wpDzl19+CRQlyXbYaeTLl09uuOEG+eCDD5LsD3cDXur0DJhwjw01Pu/qoZLySDx/rsFxMSxfvlxNWYWS9hcgHvz1QljH+BAHH98AJY14DCRAAiRgIgG7BcZnn30mkTjUOn36tJQrV069kKF3OSUBL3v+7tkpSdP3WAoMXyIe/g/X4Hny5JHmzZv7pXD8+HF59dVXVe+GbwQ9/GEde8TJC+GgrbF1l5y1pwPdjRjbjKYls29Z+Z8ESIAEwiGAe5a+jwU6DveyUIcXpk6dKtu3bw+UVNDtf//9t9SvX1+JjNGjRweNG2wnRJP1fh0sbqT7KDAiJefC46CocdKtX78+aO3mzp2rvM6dP38+UTzdE4E08IHRp1VMIDK6ESE6sB9GUfiGuEju4k2UEf+QAAmQgIMJ4OXr4sWLKarBY489pu6fAwcODDsd/UIYqiAKO4P/HkCBESk5Fx6HdUGw4E4oYeXKlTJ8+HC/dhk4ea0zR/ylhxPbV3z4i8dtJEACJOAmAt99952E4wIgWN3haRkvaV27dg0WLck+GNr7s4dLEjGFGygwUgjQLYfv2rVLuQZ/+umnQ67S2rVrBc5gfv/995CPYUQSIAES8DIBzAKBa3C7AryAQmQ8/PDD8tdff9mVrC3pUGDYgtH5iWjX4Pv37w+rMh9++KFMnDgxrGMYmQRIgAS8SgCOtQIZy0fKRA9v16lTR06dOhVpMrYfR4FhO1JnJghPcbfddltEhZ8+fbosWrQoomN5EAmQAAl4icD48eP9ugZPKYMFCxaonoy77rpLDhw4oNY4ifcwNAVGSlvVBcdjqANdbBjuiCRcvnxZeYL74osvIjmcx5AACZCAZwhgSOOnn36KSn03bNgg6dKlU74ycE/HX5KiVQAAC1BJREFUBy+OdveYhFp4CoxQSbk4HpYFxokIL56RBijmF154QSA2GEiABEiABPwTeO6556I6a65Lly7qfq4FBr4rV67svzBR3kqBEWXApievXYPbcQLCcMkOD3OmM2P5SIAESCBUAlevXpULFy4or51YsKxz586yY8cOgbOtTZs2yZo1a2Tp0qUCL8rwmDx58mS1ANnIkSNl8ODB0r9/f+XkEDNF2rZtKy1atJAHH3xQ6tatK9WrV5cKFSoI1ikpVKiQ8mOUNm3aJAIDIiMergAoMEI9S1waT7sGt8Phym+//aYuBHibYyABEiABEwmglxU+fH7++Wf5/vvv5eDBg8pBFhxfwWZh1apVgnVC4O/nnXfekTfeeEP5/YEh/KBBgwSLQWK2XadOnaR169bKMeH9998vMLC8++67lafNO++8UwoWLCi33nqrWgDt+uuv9/vQt/YywAV41qxZ1XojEAsQDRUrVpQaNWoox1rwgtyyZUu1OFm3bt2Uq3Es4wB3Aa+99poqJ8pbu3btJHnBxXg8AgVGPKgblGeHDh3UyWhXkZYtW6aUuF3pMR0SIAF3E/jjjz/U8OzJkyfVwooYboU919atW+Wjjz6SFStWqEXB3n33XbX4ImatwaMwbBnwgMWaHnjg4l7WqlUradq0qTRo0ECtfFqlShW13gYWb4QtQvbs2dWiYalSpUryELY+7NELcNNNN0muXLmUQ0AIBrjohoC49957pVGjRqonAT0K6FmA4yw4vMJqpPCuOWHCBFVWlBkLmsFvEKanbtu2TYmZQ4cOKXGDlzH0bqCXw67w1VdfSZYsWRLVLxK35HaUhwLDDooOTQMOX+AaHA627AroxXjqqafoG8MuoEyHBGJI4Nq1a3Lp0iX597//LSdOnJDDhw/Lvn37BH5yYCi4bt06wUvEwoUL1ZIBcHmNWRFwHIWHKx6yvXr1kieeeEJ56MUb90MPPaTewDFTDd35JUqUkNtvv11uueUW5dUXRonWh7vvb4iBDBkySLZs2SRv3rxyxx13KNEA8YCl0hs2bCjNmjVTvQnoVUDvAlaCxvACDNexmOKUKVNUeTHTAuWHt+LNmzermRYQNEePHhUIHAwjmOZLIpLmR9tBhKHHZcuWLZEkYcsxFBi2YHRmInruNGaR2Bkw3BLv6VF21odpkUC8CFy5ciVh/B5rAX3zzTeyd+9eNX6/cePGhPF72D/hutPj93iw6vH7Hj16CAz/8LYNZ0wPPPCA6s6vWrWqelDjgY23ezzA8SBP7u0eggDu/iEQIBQgGCAcrF35jz76qOpR0F35MAC3duVjajuGIOBREjYIsEWATQLeviFq8ICEyIETPyy2yOBMAhQYzmw3W0qNnovrrrvOlrSsieAm8frrr1s38TcJuIIA3m4xfg9nRnCHr8fv0fWNLnCM38PQGc6U9Pg9xsdffvll9TaJGVvo4cOqxejOxzWIhavwcMZDunjx4mrsHl3z6KIPZLCn3/Jx/d54442q6x/j7BgKwOKBEA/WrvzHH388UVf+Sy+9lKgr/7333kvUlQ97BLjzR1c+hA2WFbe7K98VJwQrEZQABUZQPO7diS5PGBV17949KpVENyluSAwkEC0CeLPV4/fwK4DVgLWDIXQL6/F7OIHT4/cYG3/llVfU+D2mC+I81db5eLuHsR6M5ND9Xrp0aSlSpIjqlofxHa4X/WAP9A1jvptvvlkZ91kN9TA8ALsA2AdgkSrfrnzMGLB25WMIQnfloy6wSdBd+RA3bunKj9a5wXTNIECBYUY7xLwUeKPCTRK9DdEIGH6h461okDU3TT1+f+bMGfnxxx8Txu937tyZMH4P1/IYB581a5Zg/H7cuHGCh+uLL76orPPxdg9jPXSxw2q+Xr16aipe+fLlBYZ2WIEXb/eZMmVSC/MFetBje+rUqSVjxoySI0cOtbJvsWLFBF4OYaiHKX6Y6vfII48oWwFrVz6ujTFjxiirfHTlY/gB0wh1Vz7qY+3KP3v2LLvyzT0tWbI4EqDAiCP8lGaN1fCsN1jcfGFoFUrAGxUMPKMVVq9eraZ6RSt9pps8AT1+D0t1PX6/Z88eNQcf4/doI4yB4wGKB+mkSZMSrPNhrAfLeLzdt2nTJmEqHozq4DMFb/eFCxdW5xAs1tOnT5/oXLSel/o34iAuzjscW6pUKalUqVISQz3YC2CVyAEDBqjzGT0OmDnw1ltvCbryMQShrfLRlY86WbvysQy2nVb5yZNmDBIgAX8EKDD8UXHINty48RCAQSU+Q4YMUTd5PASCBe0aHEZX0QqwPOciaInpYvweXdt6/P7rr7+WL7/8Uk1dw/g9Hprozp89e7Z6u0eXOYz1YAmOsXsMZ7Vv317NhYdlPt7Cq1WrpqbP4e08f/78kjNnTvXWjrd3/WD3950mTRrVC+A7DQ+Oe9BrgPQxAwC9CcgX+aMcvlb56Mpfvny5ssrXXfmoF6zyUU/YK9C7a+LzgP9IwCsEKDAc2tIwwMKDA9/WAEtybA82iwPzxhEHVtrRCnBiA8FjasD4PSzU0b2tx++xkqyejgcRhrd77WwHYglv0jCOw5s13rDxpg1HO5gih6ly6FHCGznezDH+njt3bvXGHqqTHT0ND+P+6CGAHQDsAWAX0Lx5czULwDrnHn4AMBUNPQ8wKNRd+Sg7rPLRlQ+hh+nIsMpHXWGzwEACJEACsSBAgRELylHIA2+3EAn+Arb7e7jj4aSnoOFNN5oBb+voXQk1YPweXdsYv4c7XUzHQ9c3rPOxgA+c7ei595jTjlkq2rOedrSDt3uMqWs3uhhrx5g73u5hYY+xeIzJw/IejAJ9YLmvp+HBGx8s+32n4WEGAGYCwGYAnv0wJRC2BLApgG2Br4Md3ZWPemmrfNQX9WYgARIgATcS8P+EcmNNXVandu3aqTdmf9UqU6aMMpCz7uvdu3eSByp83AcK2p0uurlhna/f7rXvfLzdYyre22+/rYZC4L0O9h9IE/Pu4W8fU+YwDQ/W87D5gNtbuL/F3HntQjcUJzt6Gh7m6mPOvp6GB9e8mNMP3/yYhgfnPpgV4Os+F706cIkOA0M4CrJ25WOqIbvyA50F3E4CJEACkROgwIicXVyPhIgI1EOAsXjfHgx4wPN9Y8fDPVwXutZpeBAK2l8+BMR9992XZBoeBAfKAk9/8PhnNdSDzwAYG1od7GC4gl35cT21mDkJkAAJ2EKAAsMWjLFPBGIBb+a+AUaE2OcrMCAEfAUGegSwep92nwu/AfD/D8NDOBBiV74vXf4nARIgARIIlQAFRqikDIoHA06IBXTv+wZt5Om7T9tsWEUGZ3n40uN/EiABEiABuwhQYNhFMobpoHcCRoi+Ab0X8IWB2Qz+wrRp09TURkxDhO0EAwmQAAmQAAlEiwAFRrTIRjFdeDj0FREQFzB+hPDw7b2IYlGYNAmQAAmQAAn4JUCB4ReL2RthxIkpmTCQxMwN/Mb6BzD89PWLYXZNWDoSIAESIAG3EqDAcGDLovfC+kGPBqaNMpAACZAACZCAKQQoMExpCZaDBEiABEiABFxEgALDRY3JqpAACZAACZCAKQQoMExpCZaDBEiABEiABFxEgALDRY3JqpAACZAACZCAKQQoMExpCZaDBEiABEiABFxEgALDRY3JqpAACZAACZCAKQQoMExpCZaDBEiABEiABFxEgALDRY3JqpAACZAACZCAKQQoMExpCZaDBEiABEiABFxEgALDRY3JqpAACZAACZCAKQQoMExpCZaDBEiABEiABFxEgALDRY3JqpAACZAACZCAKQQoMExpCZaDBEiABEiABFxEgALDRY3JqpAACZAACZCAKQQoMExpCZaDBEiABEiABFxE4P8BALozqDvad4AAAAAASUVORK5CYII=[/img]
In triangle [math]ABC[/math], angle [math]A[/math] is 75º and angle [math]B[/math] is 20º. Select the triangle that is similar to triangle [math]ABC[/math].
Sketch a pair of rectangles that are similar.
Determine if each statement must be true, could possibly be true, or definitely can't be true. Explain or show your reasoning.
Two line segments are similar.
Two angles are similar.
Figure G' is the image of Figure G by a dilation.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANsAAACWCAYAAABXRf3yAAAXAElEQVR4Ae1dCXRVRZpmbAZ6cIFRu2mdHoioiMAIjEArAomgDELL0gr2ATmg0wK2QGhGBwRpaEQWGRukBdmTyCIIJGHfISBbQvaQlUDIHtYQCBDWf85XyQ1vzbv3vbvm/XXOO/e9e+v+9ddX9b2q+qvqrzrEgRFgBHRBoI4uqXAijAAjQEw2rgSMgE4IMNl0ApqTYQSYbFwHGAGdEGCy6QQ0J8MIMNm4DjACOiHAZNMJaE6GEWCycR1gBHRCgMmmE9CcDCPAZOM6wAjohACTTSegORlGgMnGdcAlAjk5ORQVFSU++M7BdwSYbL5jWGsklJaW0tSpU6lRo0ZUp04du09AQABFRETUmrwakREmmxGomzBNEK1t27aCYEOHDhXEOnDgAOEzd+5catOmjfhuQtUtoxKTzTJFpZ2iIBpas4YNG1JCQoJ2Cfm5ZCabn1cAZD84OFi0aGjFOGiHAJNNO2wtIRnGD4zPAgMDLaGvlZVkslm59FTQHeMxkI2NHyqA6UEEk80DQLX9MVo0kA3jNtuALiUsk9IHpOTgGwJMNt/ws/zbsDI2bdrUKR8SCaUpAO5mOkGk+AaTTTFktesFT+M1aUw3ZcoU1TJeVFREu3btopKSEtVkWkEQk80KpaShjiAbJqzdhZCQEFUtldOmTRPypBZz1qxZ7pKudfeZbLWuSJVlCN1IVHx3S7KkaQHHMZ2yVCpjJyYm2hFNIlxGRoY34iz3DpPNckWmrsLoHqLS9+vXz6VgjNVASKXhUsUd2pxzmf52ooCGHzhDfbZl0rMfT3VJtmdGz6DeWzNo0vF8+jHrIqVevqE0OUvEZ7JZopi0VVJq3bBcC9ZHaQEyvoOIWL7lKZwpq6AFKSU0ZG82PbcqkeosOF79eXJ5LLX+MYlenh7qkmy/m/MjvbQ2uTo+3n1kyQlB0oOFVz0lbZnnTDbLFJV2iqKLiBYOy7Wkrh2u+N23b98a10SuzLxAQZFp1UR5dMkJ6rE5naadKKC9+WV04849O8UHDhxol8aQIUPsnsecK6clqedo6N5sarTshJD727B4mng8jwrLb9nFtdoPJpvVSkxjfTF287Rs6+SlG/TxwRxquLSSDGi5Pj2SS/EXymVpt3HjRpo8eTJFRkZ6jL8n/wqNOpRDv1oRJ4jXb3smWbW1Y7J5LG6OICGAlmXgrlPVrVjn8FRanXVReqz5dWnqOWq+urKL2mZdMh0tvqZ5mmomYCmy2a5qCA0NFWMLNaxkagJaW2V9HV9E/7I4RhDt7W2ZhNbNqLA9t5T+86cUocvoQ2ep/LZ9V9UovTylaymyYfyA1Q6wkEkrHLA1xFO3xxMI/Nw9AsXXb1PH9SdFxW71YxJFFZa5j6zSExhkMOVQU7h7/z7Nii+kXy6KIYzpduVdqSm6KZ5ZimwYsNuuZECrBtLBisZBfQRALIyVGofEEbpw9+6rn4ajRGkSHeUqJ5wuq6Au4aniz+D9Pdl0ueKOnNcMiWMZsknLhhxbMcmKZgh6tTjRmXGF9IuF0dRpY6quFRg9F7RssIYqCYtTz9FjS09Qk7B4wjSEGYOyHBmYA2wBcVUA+AeUMw9koOqWSvrq7bv01pYM0VJ8sO803dGjOatCCDsLQDb8oboqa09AZl25SU+HxtOvV8QRvpstWIZsaMGwhs92wjUoKEisbmAjiTrV6ubde9RuXYpo0eYlFasjVKYUlCHG3+hGuuvFyBGVe+0WPbMygZ5YHktJF6/LeUW3OJYhG1owR+MIxmpMNHXqCgwOPatatJ+yL6kjVIEU/JmifKWAls1xyCA983Q9d+M2tVyTJLqVx0rMMz1gGbIBfNsNjCAZrJM1rVj3VCj8/AECMC5gmRRM/HoHtGRSqyalDeLZGsOk+3KvpRV36eWfUsR0xaEicyz5sgTZ4PEJZHP0/CT17R3vyy0QjleJABYLg2ifHDTGGatkEEEZ2358IRtyhvk3WCofXhJDZ68abzSxBNkkc7AjOdzdd4zHv90jcKCgTBBtwM4s0sGy76SIND5DWeLPU/pg2CDX/O8k1OYGCNf0hwR6LTzVkPzZqGKNA+zxz+cIPAoFXQ90JTl4h0DZrbv0VEgctViTRLd0tDraauuOVGjV1Jo/PVx0VfyhzE3U1+hjm098t0TLhi0gIBasj/jgO7obICEbSByLVP7vQbtPUd3vow2z2knDAFwdg+T1y/G+t7+xmBmrTbINnBKwBNmkroXtFd0PDt4jEHnmsvi3x3jNqOCuVYM+EhHV+jPFtAa6kx3Wp+iyEsYVppYgmyvF+Z73CJy/cZv+dVmssNYZ1Hv0Xnkf3kR38p8WHKevYgt9kOL9q0w277Gz7Jsjos6IVk3u/jPLZtSF4v9zJJfqL4ohjFf1DoaTrby8nOBxqX///jRz5ky6d88a2yX0Lii10sNC3XrfR9N/bUlXS6Sl5MA6CbL93QBjieFk69ixo93cSrdu3SxVeFZTdnJ0vmjV9FpZMWnSJGrWrBk1b96cpk+fbgq4hu07Lfyk6D3VYSjZpMXFthOZ+O7KOmWKUrK4EvAHgrEafIToEb744gu7P1KU7Zw5c/RIusY0pKmAnbn67oEzlGxLly51KgwUyPr162sEix96hwBcGGCliF6t2nPPPedUvh06dPBOeZXf+tWgcdTo+daEntW3336rsnTX4gwlW3Z2tlNh1KtXjy5cuOBaW77rEwLv7MgSLuV8EqLg5RYtWjiV76uvvqpAgjZRYRtw7E3NmzdPm8RspBpKNugRFhZGTZo0EZnHPyG3ajalo/JX+BCBSzi9wowZM5wq9XfffadX8m7TadWqlZNeerS4hpNNQqSw0Ji5Dyn92n7dlFM5iX1c5y0n33zzjeiqderUiRYsWGAKmP+tmXP3tl27dprrZhqyaZ5TP08AFjhsqNTbAmcm2H8uukr9d2RRnd5/cmrZZs+erbmqTDbNITY+AWwMhafi/95/2nhlDNAg7fIN+uhA5UQ+LLERZy6LvXIYtrzwwgu6TUkw2QwofL2TxEEVsEIuTzuvd9KGpodlaROO5YnF1u1/SjE8/0w2Q6uDPolvySkVZDPLjmWtc431nv+XUCSc/zRbmUBzEorousOZA1rr4Eo+k80VKrXo3vjx46lR46epzuO/oXGfT6pFOXOdlZD08/Qfa5PFOQSfH8uj/GvmOYyDyea6zGrFXSyVcpxPgjm+Nga03q9XnaaDhdZm86wFzJlstbHmVeXJ1QoOPUzcekKKwzXe3Zkluslw7QA3D2YNTDazlowKerVu3dqpZTPDCg4VskZZpTdpZNVWoe6b0mjjaf3d7ynNB5NNKWIWij/iiy+dyLZw4UIL5cBZVRwfjOOAsQkUDmVxBoFVApPNKiWlUM/ssgoxid1yxGTq9Fpn4TBp8eLFCqWYKzoc9sBBUZMfEmh2fCHBVbqVApPNSqUlU9c79++L88twTnVGqfl83svMRnW0HzIviFbs4cUxNP5onil8QFYrp+ALk00BWFaJiiVJWJq1L9+8xgI5WOLQwzc2pQvjB1aAWN2NA5NNTqlbKM7Yw2dF5QzLsO42pehz1+iPVccJY1vQXov/aUjVh8kmIVELrnOTigXRZsRZcwcFDjb85FCOyAPmzIw44EPLasBk0xJdHWWHV/mBNMpfvy9ZvXLrLk2JqfSNgnHmopPWsTAqyTeTTQlaJo0bd76cGiyOoX7bM+m2xRxBzk8uEUcJ4xBDtMggXm0NTDaLl+zFm3fo+VWJ1H59immPt3UF8Zqsi2INY71F0fTpkVxL6e4qP3LuMdnkoGTiON02pdFToXGEjZFWCLvyrgjvXtjy8+H+0xR7vtwKaquiI5NNFRiNEYIzr1Fp1566aIwCClJFV3dw1YGL6O7uztPXjZwCVTWLymTTDFptBU+NqTzA8JsE/U8KVZIzHEI45ufK6QgcTGiFPwYl+VMSl8mmBC2TxMWeLbRofzl81iQaOasBN9/Tqk40fXFNEi1MKXGO5Gd3mGwWK/D9BWViEe7AXadMq/mClBJ6fFks/XpFHE2PLSAsHubA+9ksVQcw6fvbsHhxZG1huXl2IEsgrjt1kVquSaKHFh6ncYdz6ZSBBw9KOpnpyi2bmUqjBl3gIet3G05SwA8JFHPOXBY8LKfqVrVLGi7zsNyKgzMCTDZnTEx55w87ssRRT3DDZpaQeOE64ahgjB9/vy2Dduh8UIVZcJCrB5NNLlIK4+F42rFjx5IaxxHDEIIK/Y9kcxgZ8stviW4idHplw0nCgR0cPCPAZPOMkdsYONoqKipKfBzPfg4JCRG7pH09/mpe1eJi+D80OuBcahyRC5Jh1QrIb7HVYYZCyGRTCD/IM2zYMCd3A/Bi1bZt2+qWbOjQodS0aVOF0u2jo8uIij1kb7b9AwN+LT55jh5bekKc74ZD7y/cZAuj0mJgsilATGqtGjZsKNxXg3jSJzg4WLgekMSBaIjvbcBGySeXxwrDA9Y/GhU2nL5EzVcnCtIH/3yWMmvBzm+jsGSyyUReOiW1TZs25NhldBSRkJBAIKSneI7vSb8xL9VmbTK9sDqREi9el27reo0qLKOuEamCZFhmpdcBirpmUufEmGwyAAdpAgICRLdQDoHmzp1LaOm8DW0+nUN1X+1N74wYQ+np+hzJK+macukGvVe1S7rnlnTadrZUesRXHxFgsskAEOTBmExut7Bv377VYzcZ4u2itBn8sd148JFHHqG0tDS7OFr8KL5+m9BNxBgR23VWZlrXrYIW+Kghk8kmA0V0HdEtlBumTJkiN6pdvCnHc6lO3bp2ZAPJx4wbYxdPzR/YbDozrtLCiAnzb5OKLbcBVU08tJTFZPOALrqNqPBorRwDSDV16tTqj7dm/sQLMTRs3wjqEtLciWhI+zdBDemv0aPpSPE+RxV8+r0s7TzBPRzObvtrTD6V3Ljtkzx+uWYEmGw14yOsjajwjq2VREI8kz4woigJO3MjaPiBP1D3yJbUeWMX6rHpb/RSx5eq5UlyR835iAbtfkPEG7z7TQI5fQmYUnh2ZaWFET5LcFggB+0RYLJ5wBitlSuy2b4GIiKOktUis+M+F+T5OGoItVs3n+DoJv3yDUpOTiacPw15Dz30EH322WfVSYFkww/0F+8tTJlVfV/uF+zmfi280sIII8jhYmvs7pabP7PHY7J5KCE5ZAsMDJQ9prt2+6roEqI125EbIY45gkPVvfn2O5cLCgqooqLCpXZh6d8Jwn0dP9Hlc8ebaLneqTrppfumdNqcY571lY661ubfTDYPpYvWCq1MUFCQ25gwnrga07l64S+HhwqioAv5fpWbAG8cquJ9EHZB8kxXyYh7OOZW8sPYdl0yhVrYcavbTFroAZNNRmGh5QLhXI3JMIGNZ45jOldi0Q0EQTZkhwmf9TCz++JQVWrhNkdvtOvCYr3il7GVbhOw/+3vicVUcfeeK5VUvQcspLWiuCrpVquqiEmFMdlkFIy0IgSkwrrI0NBQUalw7devnyCbHEskxlswdMxPrvRc7KtD1cLCQnqq7ZMifejWp08f+j6pkOoviqFfLoqhicfzqOi6fhZG6IBpEunPCb/RI5CzEEBGMVg+CpNNZhGCcOgqogLZfrAGEouOPVWow0V7q7p9++gXC6OFQ9Vbd+/LTN11tEGDBtnpIvTqPoiGHzhDJy/pa2GUxrbASQroCaCLXVMXXIrrD1cmmxeljO6Rki7Sxo0b6a0Pu9NLo5+hJmHx1EElh6pPPPGEE9mavdjKixz5/oq0ysZRkrR425aEjnH85TeTTeOSHjlypB0h6jVvR4dUcKi6NecwNXz+cTvZaNnkGmrUzjZad3QfHYNkYJK71M3x/dr0m8mmYWlmZWU5kQGEWLVqldepZpTm0u+3vie6pC3HtXCSv2fPHq9l+/IiutPujETIs7tnvqRptXeZbBqWGCq+GEc5jPOmTZumONXi6wU0aPdYQbKgiPYU/HMI3bhzj44cOUITJkygyZMnU1JSkmK5arwgraZxZa2VWjY5BiQ1dDGzDCabhqVz9epVqlvvn50It3//ftmpYhJ8zKGvKTC8PQWGv0zv7/mKsq6Yy+eHZBxxNY6VxmyunskGoZZEZLJpWJDzk45RizHPUN0GDwg3caK8VR9Qa2bcano9or1ozfpuG03RJeZw+OMIGbqI7lxAYByH6QAO7KRVszqwM6+Q0N3rFtmL0i6W0NGjR+n8+fOy0luRtpVejwgUJOuxeRhFnsmQ9Z5RkWCUcWWYkSyU3IWsLBlu2TSooamXL1BgRC/RKkWeiZOdwvbcw/TmpoGCZK9HvEvzk/fKftfIiJhLszWAoMsoOUWyvW+kjmZIm8mmcilgmrrH5lGCMEtSo2VJz7qSR29v+1C8ExTRlSYcDZP1nhkiSQYQeBbD5HWjRo3EGBVdR1cGEzPobJQOTDaVkX93x3RBms+OhHqUDOPHH3c9sDCOjPoHXbttrWNuQTa0Xvig24guI09guy56JptrXLy6++eDKwTRBu+u2QgCko06NLvawjho91eUXmouC6NXAPBLNSLAZKsRHvkP5yQcFeTpvfWDGl/6KnaVMJxg9f/bW0fRvgLjHbDWqDA/VA0BJpsKUK49lVZFoF509prrjZnL0rZUWxjf3DSANpzW10Wdt9lMTU0Vk+ZYdhYZGemtGH6P2PTvcyXA3FfX8LeE5XG/i1YKFsY3qiyMQRHv0txEY5ZTeZPR2NhYqlevnt2k/OzZs70Rxe8w2XyrA6UVd6l75DAxTgtNt3fCc6Ysn/psGy2eBYZ3pf+VYTDxTRv13x4+fLgd0bD0rHHjxuon5CcSuRvpQ0H32TZekOnzYw9M9TB+DN49SdwPiniZPjown8puWcvCKEHSu3dvJ7KBcNevG+MSXdLLqlcmm5cl96f9ywWhPtg3Q0gAyf588IGF8b1d0+nkJWt7FZ43b54T2Xr06OElYvwak82LOjA99rAgWr/to8XbX55YRV3Cu4p7vbeOot155j1cXml2R4wYUU24zp07U2ZmplIRHL8KASabwqoQlp4qTPxvbOpFi09uoaCqNYzdIwdQWIb9uE2haNNGxxaa3Nxc0+pnFcWYbDJKqmfPntSgQQN6+LFH6dlhzUQL1j2yt7gGRbxFcxKsY2GUkV2OohECTDYPwHbp0qW6GyVtBH3xk6epa3hXGmdBC6OH7PJjDRFgsnkAt66LU2Ue/fdH6XKFcaeBelCZH5sUASabh4KBv32pRZOuSo6P8iCeH/sRAkw2D4XdoUMHJ7INGDDAw1v8mBFwRoDJ5oyJ051XXnmF0J2sX78+9erVy+k532AE5CDAZJODEsdhBFRAgMmmAogsghGQgwCTTQ5KHIcRUAEBvyYbfGTgFBrJb0ZAQIBwVKMCriyCEXBCwG/JBt/0MOXjCr8Z+MChKPxocGAEtEDAL8kG5zSYK2PHNFpUKZbpDgG/I5vkeo1bMHdVgu9rhYDfkS04ONitq2ytQGa5jAAQ8DuySSeFcvEzAnoj4Hdkg1GEXWLrXc04PSDgl2TjUzC58huBgF+SjVs2I6oap+l3ZMN5YZi85sAI6I2A35ENk9cYt+HUFXj4jYqKElfuWupd9fwvPb8jG4oYk9k4vM92MyimBDgwAloi4Jdk0xJQls0IuEOAyeYOGb7PCKiMAJNNZUBZHCPgDgEmmztk+D4joDICTDaVAWVxjIA7BJhs7pDh+4yAyggw2VQGlMUxAu4QYLK5Q4bvMwIqI8BkUxlQFscIuEOAyeYOGb7PCKiMAJNNZUBZHCPgDgEmmztk+D4joDICTDaVAWVxjIA7BJhs7pDh+4yAyggw2VQGlMUxAu4QYLK5Q4bvMwIqI8BkUxlQFscIuEOAyeYOGb7PCKiMwP8DrmVFBbwX9SoAAAAASUVORK5CYII=[/img][br][br]Where is the center of this dilation?
Estimate the scale factor. [br]