Il percorso didattico scaturisce da un lungo e meticoloso lavoro di due insegnanti del [url=https://liceospano.edu.it/]Liceo Scientifico Giovanni Spano[/url] di Sassari: [url=https://www.geogebra.org/u/marcellasechi]Marcella Sechi[/url] e [url=https://www.geogebra.org/u/valeriaaquino]Valeria Aquino[/url].[br][br]Il percorso si articola in quattro fasi distinte che evidenziano concetti e questioni geometriche riguardanti le coniche con l’obiettivo di metterne in rilievo gli aspetti comuni e, al tempo stesso, individuarne le reciproche differenze.[br][list][*][b]PRIMA FASE: Cos’è una conica?[br][/b]In questa prima fase si portano gli studenti alla scoperta delle sezioni coniche partendo da esempi pratici (presi dal museo matematico [i]Il Giardino di Archimede[/i]) e dalla visualizzazione in grafica 3D delle sezioni del cono a doppia falda che generano le coniche stesse. La prima fase si conclude con un'attività di scoperta in cui gli studenti dovranno sostanzialmente "giocare" con i parametri dell'equazione generale di una conica nel piano per cercare di generare le coniche richieste dalle domande che guidano l'attività stessa, senza però formalizzare alcunché.[/*][*][b]SECONDA FASE: Costruzione delle coniche[br][/b]Nella seconda fase si guidano gli studenti nella creazione di files propri che siano in grado di generare le coniche (parabola, ellisse e iperbole) a partire dalla loro definizione geometrica. Gli studenti in questa fase prendono dimestichezza con l'uso di GeoGebra seguendo indicazioni passo per passo molto precise nell'utilizzo dei suoi strumenti principali. Le attività sono sempre corredate da domande che cercano di guidare gli studenti nel comprendere perché la costruzione appena svolta rispetta la definizione di partenza, attivando un pensiero critico sulla costruzione stessa.[/*][*][b]TERZA FASE: Equazioni delle coniche[/b][br]Nella terza fase vengono fornite agli studenti le equazioni in forma canonica delle singole coniche e viene svolta una attività per ognuna di esse. Lo scopo di tali attività è comprendere in che modo i coefficienti dell'equazione determinino il grafico della conica, e viceversa come esso cambi al variare dei coefficienti scelti. Al termine delle attività gli studenti dovrebbero essere in grado di tracciare facilmente e in modo piuttosto preciso una qualsiasi conica, data la sua equazione.[/*][*][b]QUARTA FASE: Coniche e rette[/b][br]Nell'ultima fase vengono poi studiate le intersezioni tra coniche e rette nel piano cartesiano, analizzando i possibili casi e i metodi grafici e algebrici che ci portano a individuare i punti di intersezione. Grazie al lavoro fatto nelle fasi precedenti, l'analisi delle intersezioni conica/retta vengono svolte su tutte le coniche in generale (poiché il metodo di base è lo stesso per tutte), tralasciando i metodi algebrici utili solo in casi specifici. Particolare rilevanza viene ricoperta dal concetto di [i]retta tangente[/i] ad una conica, che viene analizzato in un'attività ad hoc.[/*][*][b]Approfondimenti[/b][br]Per concludere il percorso vengono aggiunti degli approfondimenti sullo studio delle coniche tramite l'uso dei calcolatori. In questa parte vengono utilizzati strumenti avanzati del software GeoGebra, che gli studenti possono acquisire seguendo le attività guidate.[/*][/list][br][b][color=#ff0000]Attenzione[/color][/b]: questo percorso è stato pensato e strutturato per essere un [i]aiuto[/i] alle lezioni e non un [i]sostituto[/i] di esse. L'intervento attivo del docente è sempre consigliato, così come l'uso di esercizi di analisi e rinforzo dei concetti studiati nelle singole attività, che sono ipotizzate come punto di partenza su cui costruire un dialogo didattico partecipato all'interno di un gruppo classe.[br]Il percorso di per sé non è esaustivo come studio delle coniche, e non vuole esserlo.

Come introduzione alle coniche è una buona idea partire dalla mostra [i]Oltre il Compasso[/i], allestita presso Il [b]Giardino di Archimede - Un Museo per la Matematica[/b] di Firenze. Nella mostra online (o ancora meglio dal vivo) si possono scoprire alcune macchine matematiche, strumenti e applicazioni delle coniche, talvolta del tutto sorprendenti.[br]Cliccate il link sottostante per iniziare la visita guidata:[br][br][url=https://izi.travel/it/471e-il-giardino-di-archimede-un-museo-per-la-matematica-oltre-il-compasso-la-geometria-delle-curve/it][color=#0000ff]Il Giardino di Archimede - Un Museo per la Matematica: "Oltre il compasso - La geometria delle curve"[/color][/url]

Questa attività è una guida per gli studenti alla creazione di una parabola a partire dalla sua definizione geometrica.[br][br][b][u][color=#ff0000]Definizione[/color][/u][/b][i]: [/i][color=#0000ff]la [b]parabola[/b] è il luogo dei punti nel piano [b]equidistanti[/b] da un punto, detto [b]fuoco[/b], e da una retta, detta [b]direttrice[/b].[br][/color][br]Seguite le seguenti istruzioni e riuscirete anche voi a costruire una parabola nel piano cartesiano![br][list=1][*]Iniziamo col creare un foglio di geogebra [u]senza assi cartesiani né griglia[/u]. Aprite le impostazioni del foglio (potete cliccare col pulsante destro, se state usando un pc) e cliccate su [i]Mostra gli assi[/i] e [i]Mostra la griglia[/i].[br][/*][*]Costruiamo due punti A e B con lo strumento [i]Punto[/i] [icon]/images/ggb/toolbar/mode_point.png[/icon] .[/*][*]Usiamo lo strumento [i]Retta[/i] [icon]/images/ggb/toolbar/mode_join.png[/icon] e selezioniamo i punti appena creati. Questa sarà la nostra [b]direttrice[/b].[/*][*]Creiamo un punto H sulla direttrice selezionando lo strumento [i]Punto[/i] e cliccando in una posizione qualsiasi della retta AB.[br][b]Attenzione[/b]: Geogebra creerà così un punto "C" invece di un punto "H". Possiamo però facilmente rinominare il punto aprendo le impostazioni del punto e cambiando il campo [i]Nome[/i] oppure selezionando il punto e cliccando di destro sul campo [i]Rinomina[/i].[/*][*]Creiamo un punto F [u]esterno[/u] alla direttrice selezionando lo strumento [i]Punto[/i] e cliccando in una posizione qualsiasi del piano. Questo sarà il nostro [b]fuoco[/b].[br][b]Attenzione[/b]: anche in questo caso dovremo rinominare il punto![/*][*]Usiamo adesso lo strumento [i]Retta perpendicolare[/i] [icon]/images/ggb/toolbar/mode_orthogonal.png[/icon] per costruire la retta perpendicolare alla retta AB e passante per il punto H, cliccando su questi due elementi.[/*][*]Costruiamo il segmento HF selezionando lo strumento [i]Segmento [/i][icon]/images/ggb/toolbar/mode_segment.png[/icon] e cliccando sui due punti scelti.[/*][*]Usiamo lo strumento [i]Asse di un segmento[/i] [icon]/images/ggb/toolbar/mode_linebisector.png[/icon] per creare l'asse del segmento HF appena costruito.[/*][*]Cerchiamo adesso l'intersezione dell'asse del segmento HF (punto 8) con la retta passante per H (punto 6): usiamo lo strumento [i]Intersezione [/i][icon]/images/ggb/toolbar/mode_intersect.png[/icon] e selezioniamo le due rette richieste.[/*][*]Rinominiamo il punto appena creato col nome [b]P[/b] e creiamo il segmento PF con lo strumento [i]Segmento [/i][icon]/images/ggb/toolbar/mode_segment.png[/icon] già usato in precedenza. [br][br]Questo punto è quello che genera la parabola. Volete sapere come?[br][br][/*][*]Apriamo le impostazioni del punto P e attiviamo la tracciatura del punto cliccando su [i]Mostra traccia[/i].[/*][*]Spostando il punto H sulla direttrice, la traccia di P traccerà la [b]parabola dei punti equidistanti da F e dalla retta AB[/b].[/*][/list][br]Il risultato ottenuto dovrebbe essere simile a quello mostrato di seguito, che potete usare per rispondere alle domande sottostanti.

Proviamo a capire insieme perché i punti tracciati determinino esattamente i punti della parabola cercata.

Dopo aver costruito le coniche a partire dalle loro [i]definizioni geometriche[/i] (vedi Fase due), in questa parte del libro ci concentreremo sullo studio delle equazioni delle singole coniche: parabola, circonferenza, ellisse e iperbole.[br][br]Per fare questo, partiremo di volta in volta dalla formulazione di un [b]Teorema[/b] che caratterizza l'equazione della conica, per poi analizzare come cambia la sua rappresentazione al variare dei suoi coefficienti.[br]Questa parte dello studio delle coniche andrebbe accompagnata dal docente con le dimostrazione dei teoremi inseriti, che qui non sono presenti. [br]Quello che troverete è invece una serie di schede di lavoro sviluppate [i]a partire[/i] dai teoremi stessi, che vengono dati per buoni, al fine di analizzare le equazioni ottenute grazie ad essi.

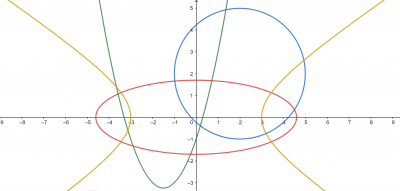
Ora che conosciamo le [b]coniche[/b] e le loro equazioni, cerchiamo di scoprire come interagiscono queste curve con le [b]rette nel piano cartesiano[/b].[br][br]Usate il file geogebra di seguito per rispondere ai quesiti sottostanti.[br]

Iniziamo col [b]deselezionare tutte le coniche[/b] già presenti nel piano, cliccando sulle quattro caselle di controllo accanto alle scritte [i]Parabola[/i], [i]Circonferenza[/i], [i]Ellisse [/i]e [i]Iperbole[/i].[br]Riportiamo i parametri della retta (in alto a sinistra) [b]tutti quanti a zero[/b], così faremo scomparire anche quella.[br][br]Adesso che abbiamo un piano cartesiano vuoto siamo pronti per iniziare a lavorarci.

L'area compresa tra una parabola e una retta ad essa secante porta il nome di [b]segmento parabolico[/b]. Pur essendo una parte di piano delimitata da una curva, la sua area si può calcolare facilmente grazie al seguente risultato teorico:[br][br][u][color=#ff0000]Teorema[/color][/u]: [color=#0000ff][i]se la retta [b]r[/b] interseca la parabola [b]γ[/b] in due punti distinti [b]A[/b] e [b]B[/b], allora l'area del segmento parabolico di base AB è uguale ai [/i][math]\frac{4}{3}[/math][i] dell'area del triangolo ABC, in cui C è il punto della parabola per cui passa la sua retta tangente parallela ad r.[/i][/color][br][br]Spieghiamo meglio, utilizzando anche il foglio di lavoro sottostante:

Nel foglio qui sopra abbiamo una retta [b]r[/b] e una parabola[b] γ[/b], in cui sono già evidenziati i loro punti d'incontro [b]A[/b] e [b]B[/b].[br]Cliccando il tasto "[i][color=#0000ff]Mostra triangolo[/color][/i]" del foglio, compare il triangolo ABC citato nel teorema.[br]La retta che completa il triangolo ha le seguenti proprietà:[br]- è [b]parallela[/b] alla retta AB;[br]- è [b]tangente[/b] alla parabola.[br]Queste due proprietà sono sufficienti per individuare i coefficienti [i]m[/i] e [i]q[/i] della retta, e quindi a individuarne l'equazione, e quindi anche il punto C in comune tra la retta e la parabola.[br]Vediamo di capire come trovare questa retta, seguendo l'attività guidata.